令和4年度（2022年）京都府公立高校入試【前期】数学の問題と解説

令和4年度（2022年）京都府公立高校入試【前期】数学の問題と解説です。
例年通りの問題量と高いレベルでの基本が試されます。
作業が重要になる問題がありますので、
慣れていない場合は基本的なとれるところ確実にとっていきましょう。

令和4年度（2022年）京都府公立高校入試【前期】数学の問題

令和４年度の京都府立高校入試の前期選抜学力検査の【数学】問題です。

⇒　令和4年度（2022年）京都府公立高校入試【前期】数学の問題

解答上の注意書きおよび正答も添付されていますのでそのまま載せておきます。

令和4年度（2022年）京都府公立高校入試【前期】数学の解説

令和４年度の前期選抜の数学の解説です。

大問で６問あります。
基本問題も一ひねりしてあるものも多いので、
ケアレスミスには注意が必要です。

例年通りだと最終できびしい問題があります。
前半で時間をかせいでチャレンジするか、それとも、、、。

第１問

\(\,\large{1}\,\)
計算が主な問題が(1)から(9)まであります。

(1)
　\(\hspace{10pt}(-5)^2-2^3\div 4\\
=25-8\div 4\\
=25-2\\
=\underline{　23　}\)

掛け算割り算部分の計算が先です。

(2)
　\(\hspace{10pt}\displaystyle \frac{3}{2}\,ab\div \frac{1}{6}\,ab^2\times (-a^2b)\\
\displaystyle =-\frac{3\,ab}{2}\times \frac{6}{ab^2}\times a^2b\\
\displaystyle =\underline{　-9\,a^2　}\)

全体の符号を見て、割り算は逆数の掛け算にします。
分母と分子にある数、文字を見間違えないように注意しましょう。

分数線は１つにして、
　\(\hspace{10pt}\displaystyle -\,\frac{3\,ab\times 6\times a^2b}{2\times ab^2\times 1}\\
=-9\,a^2\)
とした方が分母と分子のどちらになるか見やすいですが、
慣れた方法で構いません。

(3)
　\(\hspace{10pt}\displaystyle \sqrt{6}\times \sqrt{18}-\frac{9}{\sqrt{27}}\\
\displaystyle =\sqrt{6}\times 3\sqrt{2}-\frac{9}{3\sqrt{3}}\\
\displaystyle =3\sqrt{12}-\frac{3}{\sqrt{3}}\\
\displaystyle =3\times 2\sqrt{3}-\frac{3\sqrt{3}}{3}\\
\displaystyle =6\sqrt{3}-\sqrt{3}\\
=\underline{　5\sqrt{3}　}\)

無理数の計算、分母の有理化は慣れによって暗算できる段階が違ってきます。
無理せず確実に素因数分解しながら進めるとミスが減ります。

　\(\hspace{10pt}\displaystyle \sqrt{6}\times \sqrt{18}-\frac{9}{\sqrt{27}}\\
\displaystyle =6\sqrt{3}-\frac{9}{3\sqrt{3}}\\
\displaystyle =6\sqrt{3}-\frac{3}{\sqrt{3}}\\
=6\sqrt{3}-\sqrt{3}\\
=5\sqrt{3}\)

これくらいは確認しながらで良いのではないでしょうか。

(4)
連立方程式を解きます。
　\( \begin{cases}
\hspace{4pt} 3x-(y+8)=12\\
\hspace{4pt} x-2y=0
\end{cases}\)

加減法でも良いですが代入法で処理しておきます。

第二方程式から
　\(\hspace{10pt}x=2y\)
これを第一方程式に代入します。
　\(\begin{eqnarray}\displaystyle
3(\,2y\,)-(y+8)&=&12\\
6y-y-8&=&12\\
5y&=&20\\
y&=&4
\end{eqnarray}\)
このとき
　\(\hspace{10pt}x=8\)

答え　\(\hspace{4pt}\underline{　x=8\,,\,y=4　}\,\)

⇒　連立方程式の問題と解き方(加減法と代入法の選び方)

(6)
変化の割合（１次関数の傾き）と変化量の関係です。
　\(\displaystyle (\,変化の割合\,)=\frac{　\color{red}{(\,y\,の増加量\,)}　}{　\color{blue}{x\,の増加量}　}\)

\(\,x\,\)の増加量が\(\,\color{blue}{6}\,\)のとき、
変化の割合（傾き）が\(\,\displaystyle -\frac{7}{3}\,\)なので
　\(\begin{eqnarray}\displaystyle -\frac{7}{3}&=&\frac{　\color{red}{(\,y\,の増加量\,)}　}{\color{blue}{6}}\\
\color{red}{(　\,y\,の増加量　)}&=&-\frac{7}{3}\times \color{blue}{6}\\
&=&\underline{　-14　}
\end{eqnarray}\)

⇒　変化の割合とは？1次関数の求め方と直線の方程式との違い

変化の割合は全ての関数で使います。
（１次関数に限って傾きと同じです。）

(6)
これは展開してしまうと因数分解できないでしょう。
　\(\hspace{10pt}(\,x-y\,)^2-49\\
=(\,x-y\,)^2-7^2\\
=\{(\,x-y\,)+7\}\{(\,x-y\,)-7\}\\
=\underline{　(\,x-y+7\,)(\,x-y-7\,)　}\)

もちろん\(\,(\,x-y\,)=a\,\)とでもおいて
　\(\hspace{10pt}a^2-49\\
=(a+7)(a-7)\\
=\underline{　(\,x-y+7\,)(\,x-y-7\,)　}\)
と戻す方がやりやすいですね。

(7)
２次方程式を解きます。
　\(\hspace{10pt}4x^2-4x-1=0\)

因数分解できないので解の公式ですね。
　\(\begin{eqnarray}\displaystyle
x&=&\frac{-(-4)\pm \sqrt{(4)^2-4\cdot (4)\cdot (-1)}}{2\times 4}\\
&=&\frac{4\pm \sqrt{32}}{8}\\
&=&\frac{4\pm 4\sqrt{2}}{8}\\
&=&\underline{\underline{　\frac{1\pm \sqrt{2}}{2}　}}
\end{eqnarray}\)

※
（「\(\,\cdot\,\)」は「\(\,×\,\)」の意味です。）

解の公式は導けるようになりますが、
とりあえずは使えることが先です。

⇒　２次方程式の解の公式の二通りの求め方と文章題の解き方(中学３年)

(8)
円錐が２つ底面で重ねられた立体の表面積を求めます。
（体積ではないので注意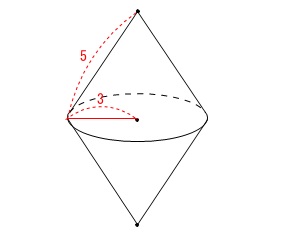）※長さの単位は\(\,\mathrm{cm}\,\)です。

底面の半径が\(\,\color{red}{3}\,\)なので、
１つの扇形の弧が\(\,\color{blue}{6\,\pi}\,\)です。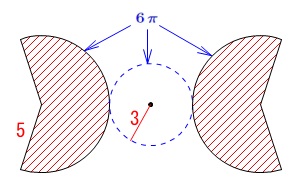公式を使えば求める表面積は、
　\(\hspace{10pt}\displaystyle 2\times \frac{1}{2}\times 6\,\pi\times 5\\
=\underline{　30\,\pi　}(\,\mathrm{cm^2}\,)\)

同じ半径の扇形の面積と円の面積は中心角や弧の長さに比例するので、
母線が\(\,\color{red}{5}\,\)の円錐の側面について、
半径\(\,5\,\)の円の円周は\(\,\color{red}{10\,\pi}\,\)、弧の長さが\(\,\color{blue}{6\,\pi}\,\)なので、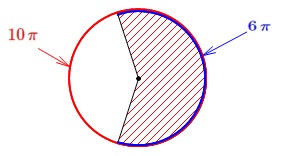扇形の面積は円の面積が\(\,\pi\,(\,5\,)^2\,\)だから
　\(\hspace{10pt}\displaystyle \frac{6}{10}\times \pi\,(\,5\,)^2\\
=15\,\pi\)

これは扇形の面積を\(\,S\,\)としたときの比例式
　\(\hspace{4pt}\color{red}{10\,\pi}:\color{blue}{5\,\pi}=\pi\,(5\,)^2:S\)
を解いただけです。

これから求める表面積は２つ分の
　\(\hspace{10pt}\underline{　30\,\pi　}\,(\,\mathrm{cm^2}\,)\)

扇形の中心角は
　\(\hspace{10pt}\displaystyle \frac{6}{10}\times 360^{\circ}\\
=216^{\circ}\)
ですが中心角を使うか弧の長さを使うかはどちらでも良いです。

(9)
代表値の比較です。

⇒　代表値とは？度数分布表の平均値,中央値の求め方と最頻値の答え方

平均値、中央値、最頻値を全て求めておきます。

（ア）平均値
　\(\hspace{10pt}\displaystyle \frac{0\times 14+1\times 13+2\times 12+3\times 2+4\times 1}{42}\\
\displaystyle =\frac{47}{42}=1.1\cdots \)
※
実際には中央値と最頻値を先に求めているので、
小数第１位で計算を終わらせています。

（イ）中央値
小さい方から\(\,21\,\)番目と\(\,22\,\)番目の平均になるので
　\(\hspace{4pt}1\)

（ウ）最頻値
　\(\hspace{4pt}0\)

答え　\(\,\underline{　（ウ）\rightarrow （イ）\rightarrow　（ア）　}\,\)

代表値の求め方さえ知っていれば説明は必要ないでしょう。

第２問

\(\,\large{2}\,\)
袋に入った５個の玉から２個取り出すときの確率です。
　黒玉：\(\,1\,,\,3\,\)
　白玉：\(\,\color{red}{1}\,,\,\color{red}{3}\,,\,\color{red}{5}\,\)
（白玉は文字では白にすると見えないので赤にしてあります。）

２問とも２個玉を取り出しますが、
取り出した玉を戻す場合と戻さない場合があります。

どちらも樹形図で良いですよ。

(1)
取り出した玉を戻す場合です。
初めに取り出した玉と次に取り出した玉の数が等しくなる確率を求めます。

色違いでも同じ数があることに注意して、
ここでは表で見ておきます。
縦、横どちらがはじめに取り出した玉でも構いません。
　\(\begin{array}{|c|c|c|c|c|} \hline
& 1 & 3 & \color{red}{1} & \color{red}{3} & \color{red}{5} \\ \hline
\,1 \,& ○ & & ○ & & \\ \hline
3 & & ○ & & ○ & \\ \hline
\color{red}{1} & ○ & & ○ & & \\ \hline
\color{red}{3} & & ○ & & ○ & \\ \hline
\color{red}{5} & & & & & ○ \\ \hline
\end{array}\)

答え　\(\hspace{4pt}\displaystyle \underline{\underline{　\frac{9}{25}　}}\)

(2)
今度は同時に２個取り出します。
これは１個取り出し、戻さずに２個目を取り出すことと同じです。
　\(\begin{array}{|c|c|c|c|c|} \hline
& 1 & 3 & \color{red}{1} & \color{red}{3} & \color{red}{5} \\ \hline
\,1 \,& × & & & & \\ \hline
3 & & × & & & \\ \hline
\color{red}{1} & & & × & & \\ \hline
\color{red}{3} & & & & × & \\ \hline
\color{red}{5} & & & & & × \\ \hline
\end{array}\)
（\(\,×\,\)となる取り出し方はない。）

このとき取り出した２個の玉のうち、
　白玉の個数を\(\,a\,\)
　２つの玉に書かれている数の和を\(\,b\,\)
としたとき
　\(\hspace{4pt}4\,a=b　･･･①\)
となる確率です。

一応解説しておきますが、
問題の意味がとれたら樹形図でチャチャっと片付けた方が早いですよ。

取り出した白玉の数は\(\,0\,,\,1\,,\,2\,\)しかありません。
（２個しか取り出さないから。）
数の和\(\,b\,\)は正の数なので\(\,a=0\,\)のとき\(\,①\,\)を満たす事はないので
　\(\hspace{4pt}a=1\,,\,2\)

\(\,a=1\,\)のとき黒玉１個、白玉１個取り出すので、
数の和が４になる組を探すと
　\((\,1\,,\,\color{red}{3}\,)\,,\,(\,3\,,\,\color{red}{1}\,)\)
\(\,a=2\,\)のとき白玉２個取り出すので、
数の和が８になる組を探すと
　\((\,\color{red}{3}\,,\,\color{red}{5}\,)\)
だけです。
引く順番も入れかえられるので条件を満たすのは、
　\(\begin{array}{|c|c|c|c|c|} \hline
& 1 & 3 & \color{red}{1} & \color{red}{3} & \color{red}{5} \\ \hline
\,1 \,& × & & & ○ & \\ \hline
3 & & × & ○ & & \\ \hline
\color{red}{1} & & ○ & × & & \\ \hline
\color{red}{3} & ○ & & & × & ○ \\ \hline
\color{red}{5} & & & & ○ & × \\ \hline
\end{array}\)
取り出し方２０通りに対して６通りが条件を満たします。

答え　\(\hspace{4pt}\displaystyle \frac{6}{20}=\underline{\underline{　\frac{3}{10}　}}\)

第３問

\(\,\large{3}\,\)
関数の基本確認問題です。

問題にある条件は
　関数\(\,y=ax^2\,\)上に点\(\,\mathrm{A\,,\,B}\,\)があり、
　点\(\,\mathrm{A}\,\)は\(\,(\,-3\,,\,2\,)\,\)
　点\(\,\mathrm{B}\,\)の\(\,x\,\)座標は\(\,6\,\)
　点\(\,\mathrm{C}\,\)は直線\(\,\mathrm{AB}\,\)と\(\,y\,\)軸との交点（\(\,y\,\)切片）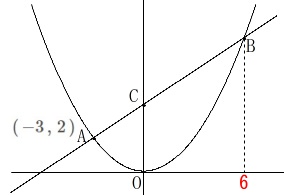
(1)
比例定数\(\,a\,\)を求めます。

関数\(\,y=a\,x^2\,\)は点\(\,\mathrm{A}\,\)を通るので、
\(\,y=a\,x^2\,\)に\(\,(\,\color{red}{-3}\,,\,\color{blue}{2}\,)\,\)を代入して
　\(\begin{eqnarray}\displaystyle
\color{blue}{2}&=&a\,(\color{red}{-3})^2\\
a&=&\underline{\underline{　\frac{2}{9}　}}
\end{eqnarray}\)

関数は\(\displaystyle \,y=\frac{2}{9}\,x^2\,\)と決まりました。

(2)
直線\(\,\mathrm{AB}\,\)の式（１次関数）を求めます。

点\(\,\mathrm{B}\,\)の座標は\(\,x\,\)座標が\(\,6\,\)なので、
関数\(\displaystyle \,y=\frac{2}{9}\,x^2\,\)に代入して\(\,y=8\,\)となり
　\(\hspace{4pt}\mathrm{B}\,(\,6\,,\,8\,)\)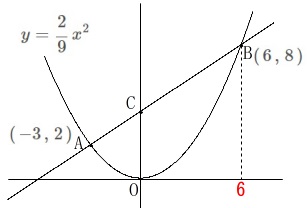２点\(\,\mathrm{A\,,\,B}\,\)を通る直線は
　\(\hspace{4pt}\displaystyle \underline{\underline{　y=\frac{2}{3}\,x+4　}}\,\)

⇒　変化の割合とは？1次関数の求め方と直線の方程式との違い

ここではあえて求め方は説明していません。
２点を通る直線の式は必ず求められるようになっておきましょう。
※
できるだけ短時間で求められるようにしておきたいですが、
ミスだけには気をつけて確認しながらですよ。

(3)
面積を求めますが条件があり、ちょっとした応用になります。

点\(\,\mathrm{D}\,\)を\(\,\mathrm{DC+DB}\,\)が最小になるように\(\,x\,\)軸上にとるとき、
\(\,\mathrm{△BCD}\,\)の面積を求めます。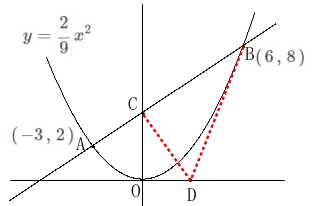折れ線の長さが最小になるのは直線になるときですが、
ここでは\(\,\mathrm{B\,,\,C}\,\)が同じ側にあるので反対に折り返します。

どちらでも良いですが\(\,\mathrm{C}\,\)を\(\,x\,\)軸の反対に移すと、
　\(\hspace{4pt}\mathrm{C’}\,(\,0\,,\,-4\,)\)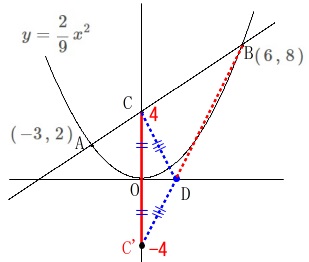このとき線分\(\,\mathrm{C’B}\,\)の長さが、
\(\,\mathrm{DC+DB}\,\)の最小と同じです。
（求めたいのは\(\,\mathrm{△BCD}\,\)なので長さは求めなくて良いですよ。）

直線\(\,\mathrm{C’B}\,\)は
　\(\hspace{4pt}y=2x-4\)
なので\(\,\mathrm{D}\,\)の座標は\(\,(\,2\,,\,0\,)\)となるので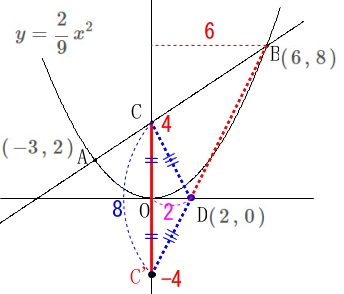\(\,\mathrm{△BCD}\,\)の面積は
　\(\begin{eqnarray}\displaystyle
\mathrm{△BCD}&=&\mathrm{△BCC’-△DCC’}\\
&=&\frac{1}{2}\times 8\times 6-\frac{1}{2}\times 8\times 2\\
&=&\underline{　16　}
\end{eqnarray}\)

この問題、単位がなくてシンプルで良いですね。

面積の求め方は他にもいろいろありますが、何でも良いです。

第４問

\(\,\large{4}\,\)
平面図形、合同の証明と線分比を求める問題です。

条件は問題文の通りですが一応書き出しておきます。
　\(\,\mathrm{△ABC}\,\)は正三角形
　\(\mathrm{BD:DC}=7:2\)
　\(\,\mathrm{△ADE}\,\)も正三角形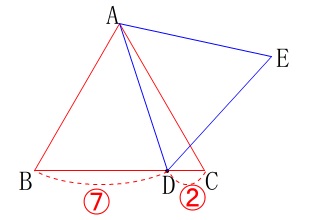長さは与えられていませんので単位もありません。

(1)
三角形の合同を証明します、。
　\(\,\mathrm{△ABD}\,\)≡\(\,\mathrm{△ACE}\,\)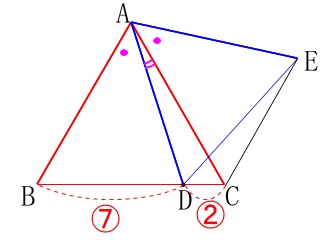図の中で合同条件を見つければ終わりです。

２組の辺は仮定から分かります。
正三角形の１つの角が\(\,60°\,\)で、同じ角を引くことになるので
　\(\,\mathrm{∠BAD=∠CAE}\,\)
　「２組の辺とその間の角がそれぞれ等しい。」
が合同条件ですね。

⇒　中学の図形証明問題(合同･相似)の解き方と証明の書き方ポイント

合同条件をそろえることができれば、
証明の書き方は好きにしていいです。

(2)
(1)に条件が
　「直線\(\,\mathrm{CE}\,\)と直線\(\,\mathrm{AD}\,\)との交点を\(\,\mathrm{F}\,\)とするとき、」
が加わり、\(\,\mathrm{EC:CF}\,\)を整数比で答えます。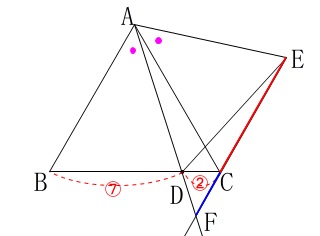正三角形の内角と(1)の合同から、
　\(\,\mathrm{∠ABC=∠ACE=∠DCF}=60^{\circ}\,\)
となるので、
　\(\,\mathrm{AB}\,\)∥\(\,\mathrm{CF}\,\)
であり、
　\(\,\mathrm{△ABD}\,\)∽\(\,\mathrm{△FCD}\,\)
（こっちだけでも気がつけば良いです。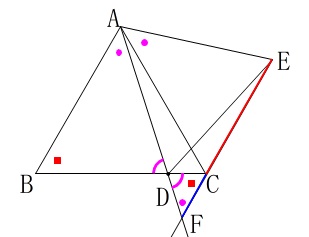）ここで\(\,\mathrm{BD:DC=7:2}\,\)なので、
正三角形の１辺との比を見ると
\(\hspace{10pt}\mathrm{AB:BD:DC}=\color{blue}{⑨}:\color{red}{⑦}:\color{red}{②}\)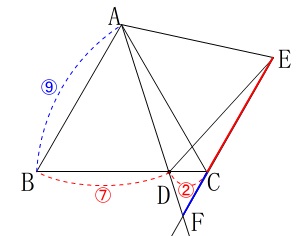このことから
　\(\,\mathrm{△ABD}\,\)∽\(\,\mathrm{△FCD}\,\)に比例式を利用すると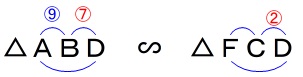\(\,\mathrm{AB=9}\,\)として\(\,\mathrm{FC}\,\)の長さは
　\(\begin{eqnarray}\displaystyle
\mathrm{AB:DB}&=&\mathrm{FC:DC}\\
9:7&=&\mathrm{FC}:2\\
7\times \mathrm{FC}&=&9\times 2\\
\mathrm{FC}&=&\color{magenta}{\frac{18}{7}}
\end{eqnarray}\)
合同な三角形だから\(\,\mathrm{DB=EC=7}\,\)なので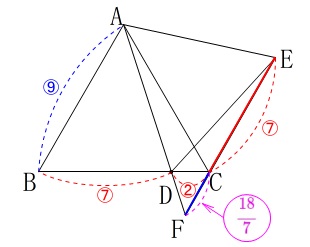
　\(\begin{eqnarray}\displaystyle
\mathrm{EC:CF}&=&7:\frac{18}{7}\\
&=&\underline{　49:18　}
\end{eqnarray}\)

第５問

\(\,\large{5}\,\)
空間図形（直方体）における線分、面積、体積を求める問題です。

図の直方体について
　\(\hspace{4pt}\mathrm{AB=AD}=\color{red}{4}\,\mathrm{cm}\)
　\(\hspace{4pt}\mathrm{AE}=\color{red}{2\sqrt{3}}\,\mathrm{cm}\)
　２点\(\,\mathrm{I\,,\,J}\,\)はそれぞれ辺\(\,\mathrm{EF\,,\,EH}\,\)の中点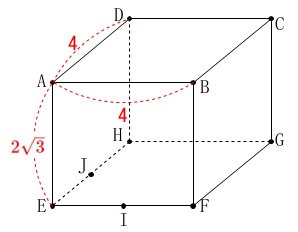正方形が上下にありますね。
(1)
線分\(\,\mathrm{IJ}\,\)の長さを求めます。

面\(\,\mathrm{EFGH}\,\)を抜き出すと正方形なのですぐに求まるでしょう。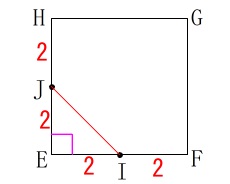\(\,\mathrm{△EIJ}\,\)は三角定規になるので
　\(\hspace{10pt}\mathrm{IJ}=\underline{　2\sqrt{2}　}\,(\,\mathrm{cm}\,)\)

三平方の定理でも良いですよ。

(2)
四角形\(\,\mathrm{BDJI}\,\)の面積を求めます。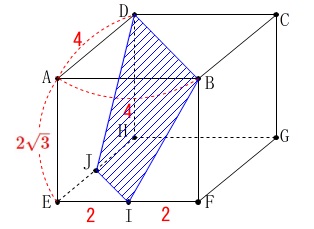四角形を抜き出して考えますが、
線分の長さはそれぞれ自分でも求めて確認しておいて下さい。
（三平方の定理を何度も使えば全て求められます。）

四角形\(\,\mathrm{BDJI}\,\)は\(\,\mathrm{BI=DJ}\,\)の等脚台形です。
　\(\hspace{4pt}\mathrm{BD}=\color{red}{4\sqrt{2}}\)
　\(\hspace{4pt}\mathrm{IJ}=\color{red}{2\sqrt{2}}\)
　\(\hspace{4pt}\mathrm{IB=JD}=\color{blue}{4}\)
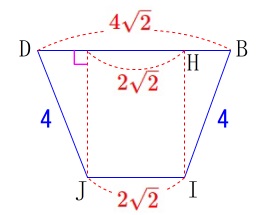このとき高さは下図の\(\,\mathrm{HB=\color{blue}{\sqrt{2}}}\,\)だから、
\(\,\mathrm{△IBH}\,\)に三平方の定理を用いて、
　\(\hspace{10pt}\mathrm{IH=\color{magenta}{\sqrt{14}}}\,\)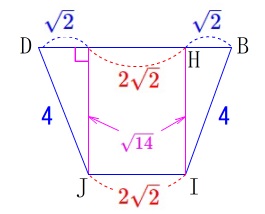これらから求める台形の面積\(\,S\,\)は
　\(\begin{eqnarray}\displaystyle
S&=&\frac{\color{red}{2\sqrt{2}}+\color{red}{4\sqrt{2}}}{2}\times \color{magenta}{\sqrt{14}}\\
&=&3\sqrt{2}\times \sqrt{14}\\
&=&\underline{　6\sqrt{7}　}\,(\,\mathrm{cm^2}\,)
\end{eqnarray}\)

(3)
直方体内にできる四角錐\(\,\mathrm{KEFGH}\,\)の体積を求めます。

２点\(\,\mathrm{A\,,\,G}\,\)を通る直線と、
四角形\(\,\mathrm{BDJI}\,\)との交点を\(\,\mathrm{K}\,\)底面は正方形なので高さを求める事が問題になりますが、
点\(\,\mathrm{K}\,\)から垂線を面\(\,\mathrm{EFGH}\,\)に下ろし交点を\(\,\mathrm{P}\,\)とし、
これを\(\,\mathrm{BF}\,\)と\(\,\mathrm{DH}\,\)が重なる方向から見ます。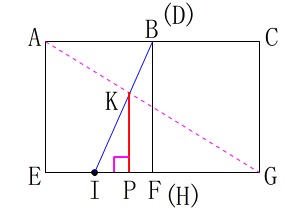この面を見たとき、
\(\,\mathrm{B\,,\,I}\,\)はそれぞれ\(\,\mathrm{AC\,,\,EF}\,\)の中点なので、
　\(\hspace{4pt}\mathrm{AB:IG}=2:3\)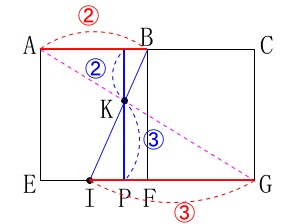\(\,\mathrm{△ABK}\,\)　∽　\(\,\mathrm{△GIK}\,\)
なので
　\(\hspace{4pt}\mathrm{KP:AE}=3:(2+3)=3:5\)

このことから高さとなる\(\,\mathrm{KP}\,\)の長さは
　\(\begin{eqnarray}\displaystyle
\mathrm{KP}&=&\frac{3}{5}\times \mathrm{AE}\\
&=&\color{red}{\frac{3}{5}\times 2\sqrt{3}}
\end{eqnarray}\)
※
体積計算が待っているので計算を進めていませんが、
整えておいても良いですよ。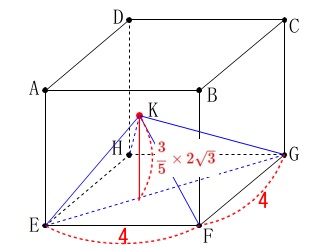よって求まる体積\(\,V\,\)は
　\(\begin{eqnarray}\displaystyle
V&=&\frac{1}{3}\times 4\times 4\times \frac{3}{5}\times 2\sqrt{3}\\
&=&\underline{\underline{　\frac{32\sqrt{3}}{5}　}}\,(\,\mathrm{cm^3}\,)
\end{eqnarray}\)

ここでは立体を横から見た図で考えているように見えますが、
点\(\,\mathrm{K}\,\)は面\(\,\mathrm{AEGC}\,\)上にあるので
四角形\(\,\mathrm{AEGC}\,\)を抜き出しても同じことが言えます。

第６問

\(\,\large{6}\,\)
問題の意味がわかりにくいかもしれませんが、
２人が座れるいす\(\,\mathrm{A}\,\)と３人が座れるいす\(\,\mathrm{B}\,\)がたくさんあり、
全てのいすであまりなく座る。
\(\,n\,\)人が座るとき組合わせは何通りあるかを考えます。

「たとえ」が問題にありますが、
逆に考えて説明しておきます。

例えば、
　\(\,\mathrm{A}\,\)１つで２人座れます。
　\(\,\mathrm{B}\,\)１つで３人座れます。
　\(\,\mathrm{A}\,\)２つで４人座れます。
　\(\,\mathrm{A}\,\)１つと\(\,\mathrm{B}\,\)１つで５人座れます。
　\(\,\mathrm{A}\,\)３つで６人座れます。
　\(\,\mathrm{B}\,\)２つも６人座れます。

これを人数を先に見て考えたのが「たとえ」です。

では、問題に入りましょう。
「ただし、\(\,n\,\)は２以上の自然数とする。」
これは１人で座るいすはないので除外されています。
これが本当は重要な（やっかいな）場合分けになるのですが、
考えなくて良いよ、と優しく教えてくれているのです。

(1)
\(\,n=20\,\)のとき\(\,\mathrm{A\,,\,B}\,\)の脚数の組み合わせは何通りあるかです。

\(\,\mathrm{A}\,\)の脚数が\(\,\color{red}{10}\,\)，\(\,\mathrm{B}\,\)の脚数が\(\,\color{blue}{0}\,\)のとき、
　\(\,n=2\times \color{red}{10}+\,3\times \color{blue}{0}=20\,\)
これはすぐ分かります。
では、全て調べ上げることはできるのか？
もれなく調べるのは難しいです。

そこで方程式にして見ましょう。
　\(\,\mathrm{A}\,\)の脚数\(\,\color{red}{x}\,\)、\(\,\mathrm{B}\,\)の脚数\(\,\color{blue}{y}\,\)とすると
\(\,n\,\)は\(\,\color{red}{x}\,,\,\color{blue}{y}\,\)を使って
　\(\hspace{4pt}\,n=2\,\color{red}{x}+3\,\color{blue}{y}\)
と表すことができます。
こうすると\(\,n=20\,\)の場合、
　\(\,x\,\)は\(\,10\,\)以下、\(\,y\,\)は\(\,6\,\)以下
と絞ることができます。
さらに、\(\,3\,y\,\)は偶数でないと\(\,n\,\)が偶数にならない、
ということも見えてくるでしょう。

なので\(\,\color{blue}{y}\,\)を変化させていく方が、
調べる数は少なくて済む事が分かるでしょう。
　\(\hspace{4pt}(\,x\,,\,y\,)=(\,10\,,\,\color{blue}{0}\,)\,,\,(\,7\,,\,\color{blue}{2}\,)\,,\,(\,4\,\,,\color{blue}{4}\,)\,,\,(\,1\,,\,\color{blue}{6}\,)\)

答え　\(\,\underline{　4　}\,\)通り

ここで分かったのは何通りあるかの調べ方です。

(2)
\(\,n=127\,\)のときの脚数の組み合わせは何通りあるかです。

今度は奇数ですが
　\(\hspace{4pt}n=2\,\color{red}{x}+3\,\color{blue}{y}\)
は同じで、\(\,y\,\)が奇数でなければならないという場合です。

\(\,3\,y\,\)が奇数の数は、
　\(\hspace{4pt}3\,y=3\,,\,9\,,\,15\,,\,\cdots\,\)
もう少し分かり易く書くと、
　\(\hspace{4pt}3\times 1\,,\,3\times 3\,,\,3\times 5\,,\,\cdots\)
となるので\(\,127\,\)以下の\(\,3\,y\,\)の上限は
　\(\hspace{10pt}3\times 41\)
となります。

\(\,1\,\)から\(\,41\,\)までの奇数は\(\,21\,\)個あります。
　\(\begin{eqnarray}\displaystyle
2m-1&=&41\\
m&=&21
\end{eqnarray}\)

答え　\(\,\underline{　21　}\,\)通り

\(\,127\,\)を\(\,3\,\)で割ると\(\,42\,\)という商が最大ですが、
　\(\hspace{4pt}3\times 42=126\)
偶数なのでその前の\(\,41\,\)が最大の\(\,y\,\)（奇数）です。
その次の奇数だと
　\(\hspace{4pt}3\times 43=129\)
なので超えてしまうことも確認すると良いです。

大切なのは奇数は文字式で\(\,2m-1\,\)となることで、
奇数の個数を求めるときに利用できるということですね。

奇数の個数分組み合わせができるので答えになります。

わかりにくいでしょう？
でもここまでは具体例を調べ上げることと、
文字式で処理できる問題です。

次はさらにややこしく感じます。

(3)
いすの組み合わせを\(\,a\,\)とするときの、
\(\,n\,\)の最小値と最大値を\(\,a\,\)を用いて表します。

すでに「何？」となります。
例えば\(\,a=2\,\)のとき最小値は\(\,n=6\,\)です。
（問題の表で確認できます。）
最大値は？
調べてみるしかありません。
ここで調べて行くかどうかが鍵ですね。
数式で処理しようとすると奇数と偶数で場合分け？
となるので、ここは覚悟を決めて規則性を見つけにいきます。
　\(\hspace{4pt}2x+3y=n\)
を満たす\(\,y\,\)の個数を奇数偶数を考えて見ていきましょう。
（\(\,n\,\)が奇数のときは\(\,y\,\)は奇数、偶数のときは偶数です。）
　\(\begin{array}{|c|c|c|} \hline
\,n\, &　 y\,の値　&　組み合わせ総数　 \\ \hline
1 & 無し & 0\\ \hline
2 & 0 & 1\\ \hline
3 & 0 & 1\\ \hline
4 & 1 & 1\\ \hline
5 & 1 & 1\\ \hline
6 & 0\,,\,2 & \color{red}{2}\\ \hline
7 & 1 & 1\\ \hline
8 & 0\,,\,2 & \color{red}{2}\\ \hline
9 & 1\,,\,3 & \color{red}{2}\\ \hline
\,10\,& 0\,,\,2& \color{red}{2} \\ \hline
11 & 1\,,\,3 & \color{red}{2}\\ \hline
12 & 0\,,\,2\,,\,4 & \color{blue}{3}\\ \hline
13 &1\,,\,3 & \color{red}{2}\\ \hline
14 & 0\,,\,2\,,\,4 & \color{blue}{3}\\ \hline
15 & 1\,,\,3\,,\,5 & \color{blue}{3}\\ \hline
16 & 0\,,\,2\,,\,4 & \color{blue}{3}\\ \hline
17 & 1\,,\,3\,,\,5 & \color{blue}{3}\\ \hline
18 & 0\,,\,2\,,\,4 \,,\,6& \color{magenta}{4}\\ \hline
19 & 1\,,\,3\,,\,5 & \color{blue}{3}\\ \hline
20 & 0\,,\,2\,,\,4 \,,\,6& \color{magenta}{4}\\ \hline
\end{array}\)
確かに(1)の答えは合っていました。

それでですね。
組み合わせの総数は\(\,y\,\)の個数なので、
いちいち\(\,y\,\)の値を書き出す必要はありません。
\(\,n\,\)が奇数のときは\(\,3y\,\)が\(\,n\,\)以下となる奇数\(\,y\,\)の個数を書き出し、
\(\,n\,\)が偶数のときは\(\,3y\,\)が\(\,n\,\)以下となる偶数\(\,y\,\)の個数を書き出せば良いです。
続きをやっておきます。
※
自分でできるだけ多くやる方が規則性が見えてきます。
試験時間からそれほど多くはできませんが京都府立入試です。
覚悟して取り組む事をおすすめします。
　\(\begin{array}{|c|c|c|c|c|c|c|c|} \hline
　n　&　総数　& &　n　&　総数　& &　n　&　総数　\\ \hline
1 & 0&& 7 & 1&&13 & \color{red}{2}\\ \hline
2 & 1 && 8 & \color{red}{2}&&14 & \color{blue}{3}\\ \hline
3 & 1 && 9 & \color{red}{2}&&15 & \color{blue}{3}\\ \hline
4 & 1 &&\,10\,& \color{red}{2}&&16 & \color{blue}{3}\\ \hline
5 & 1 &&11 & \color{red}{2}&&17 & \color{blue}{3}\\ \hline
6 & \color{red}{2}&&12 & \color{blue}{3}&&18 & \color{magenta}{4}\\ \hline
\end{array}\)
あ、周期は\(\,6\,\)？と思えるけどもう少し、
　\(\begin{array}{|c|c|c|c|c|c|c|c|} \hline
　n　&　総数　& &　n　&　総数　& &　n　&　総数　\\ \hline
19 & \color{blue}{3}&& 25 &\color{magenta}{4} && 31& \color{red}{5}\\ \hline
20& \color{magenta}{4}&& 26 & \color{red}{5}&&32 & \color{blue}{6}\\ \hline
21&\color{magenta}{4} && 27 & \color{red}{5}&&33 & \color{blue}{6}\\ \hline
22&\color{magenta}{4} && 28 &\color{red}{5} && 34& \color{blue}{6}\\ \hline
23& \color{blue}{4}&& 29 &\color{red}{5} && 35& \color{blue}{6}\\ \hline
24& \color{red}{5}&& 30 & \color{blue}{6}&& 36& \color{magenta}{7}\\ \hline
\end{array}\)
周期が\(\,6\,\)で最小値は左下に表れ、最大値が次の最小値の右上、
だと推測できます。

高校入試としては推測でしか答えは出せないと思うので、
ここから文字遊びをします。
　\(\begin{array}{|c|c|c|c|c|c|c|c|} \hline
　a　& \,\color{red}{2}\,&\,\color{blue}{3}\,&\,\color{magenta}{4}\,&\,5\,&\,6\,&\,7\,&\cdots \\ \hline
　最小値　& \,6\, & \,\color{red}{12}\,&\,\color{blue}{18}\,& \,\color{magenta}{24}\,&\,30\,&\,36\,&\cdots \\ \hline
　最大値　&\,13\, &\,19\,&\,25\,&\,31\,&\,37\,&\,43\,&\cdots \\ \hline
\end{array}\)

最小値は\(\,a\,\)より\(\,1\,\)小さい数の\(\,6\,\)倍、
　\(\hspace{4pt}6(a-1)\)
最大値は\(\,a\,\)の\(\,6\,\)倍より\(\,1\,\)大きい数、
　\(\hspace{4pt}6a+1\)
（\(\,a=1\,\)のときを入れると分かり易くはなります。）

答え　最小の値　\(\,\underline{　6a-6　}\,\)　最大の値　\(\,\underline{　6a+1　}\,\)

この周期性は推測ではなく事実です。

このことから(2)の答え\(\,a=21\,\)を見直すと、
\(\,n\,=\,127\,\)は
　最小値　\(\,6(21-1)\,=\,120\,\)
　最大値　\(\,6\times 21+1\,=\,127\,\)
の範囲にありました。

以上です。
これ以上は時間をかけたくないので終わりにします。

京都府立入試ではこのくらいの作業は恒例と言って良いかもしれません。
公式だけでは簡単に解けない問題もチャレンジして欲しいという思いではないでしょうか。

⇒　京都府公立高校入試数学の過去問と解答解説

前半で時間をかせぐ程の基本の定着がなければ、
高得点は十分狙えても満点は厳しいです。