令和４年（２０２２年）度奈良県公立高校入試【数学】の問題と解説

令和４年度（２０２２年）奈良県公立高校入試【数学】の問題と解説です。
計算から図形、関数とほぼ全分野からの出題で大問４つあります。
基本中心の問題ですので確実に一つひとつ取っていけば良いでしょう。
５０点満点なので１問の比率が大きくなるのでミスには気をつけたいところです。

傾向としては例年通りで、
過去問の傾向から基礎重視していた人には取りやすい問題なので簡単に済ませます。

令和4年（2022年）度奈良県公立高校入試【数学】の問題

奈良県が公開してくれている問題です。

⇒　令和4年（2022年）度奈良県公立高校入試【数学】の問題PDF

注意書きもシンプルなので試験前に確認して、
本番も同じかどうかだけ確認すれば良いですね。
違っていれば何かあると最終確認しましょう。

令和4年（2022年）度奈良県公立高校入試【数学】の解説

大問４つは例年通りです。

偏りの少ない基本重視の問題で、
（割と）シンプルなのでちゃちゃっと進めます。

第１問

\(\color{black}{\fbox{\(\,\large{1}\,\)}}\)
(1)
式の計算が4つあります。
①
　\(\hspace{10pt}3-7\\
=\underline{　-4　}\)

引き算は数直線で左に動きます。

②
　\(\hspace{10pt}4(x+2)+2(x-3)\\
=4x+8+2x-6\\
=\underline{　6x+2　}\)

２行目は省略（暗算）しない方がミスが減ります。
そのそも暗算するより書いた方が早い！

③
　\(\hspace{10pt}\displaystyle 12x^2y\div 4x^2\times 3xy\\
\displaystyle =\frac{12x^2y \times 3xy}{4x^2}\\
=\underline{　9xy^2　}\)

暗算できないレベルの計算ではありませんが、
いつでも使えるように分数計算にしています。

④
　\(\hspace{10pt}(x+2)(x+8)-(x+4)(x-4)\\
=(x^2+10x+16)-(x^2-16)\\
=x^2+10x+16-x^2+16\\
=\underline{　10x+32　}\)

ここまで、ミスに注意していれば好きに計算して良いです。

(2)
２次方程式を解きます。
　\(\hspace{4pt}x^2-6x+2=0\)

因数分解を先に試しますができないので解の公式です。
　\(\begin{eqnarray}\displaystyle
x&=&\frac{-(-6)\pm \sqrt{(-6)^2-4\cdot (1) \cdot (2)}}{2\times 1}\\
&=&\frac{6\pm \sqrt{36-8}}{2}\\
&=&\frac{6\pm \sqrt{28}}{2}\\
&=&\frac{6\pm 2\sqrt{7}}{2}\\
&=&\underline{　3\pm \sqrt{7}　}
\end{eqnarray}\)
※
ルートの中の\(\,\cdot\,\)は掛け算を意味します。

解の公式で１次の係数が偶数のときは計算が楽になる公式もありますので、
知っている人は使っていると思いますが教科書通り計算しておきました。
ただ、１つ便利な計算方法を知っているとかなり時間はかせげます。

⇒　２次方程式の解の公式二通りと便利な公式の求め方と文章題の解き方

次も公式ではありませんが、
よく使う手順なので覚えておくと早いです。

(3)
代入問題です。
ただ、この手の条件式では処理の仕方で簡単になります。
　\(\begin{eqnarray}
x&=&\sqrt{2}+3\\
x-3&=&\sqrt{2}
\end{eqnarray}\)
ここで両辺２乗します。
　\(\begin{eqnarray}
(x-3)^2&=&2\\
x^2-6x+9&=&\color{red}{2}
\end{eqnarray}\)
よって求める値は、
　\(\hspace{10pt}x^2-6x+9=\underline{　2　}\)

求める式に\(\,x\,\)の値を代入してもそれほどきつい計算ではありませんが、
次数が高い計算になるほど役に立つ方法です。

⇒　ルートのついた無理数の代入の応用問題と使い方のポイント

高校数学でも役に立つのでとりあえず見ておいて、
高校になって「そういえば」、と思い出せればそれでいいです。

(5)
メジアン（中央値）を含む階級の相対度数を求めます。

代表値が出せないとどうにもなりません。

⇒　代表値とは？度数分布表の平均値,中央値の求め方と最頻値の答え方

メジアンは\(\,22.5\,\)です。
その階級の度数は\(\,6\,\)なので相対度数は
　\(\hspace{10pt}\displaystyle \frac{6}{40}=\underline{　0.15　}\)

(6)
球と円柱の体積比です。

球の半径を\(\,r\,\)とすると、
円柱の底面の直径が\(\,2\,r\,\)、高さが\(\,2\,r\,\)となります。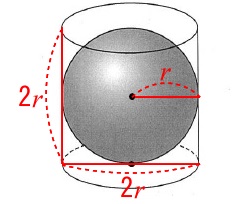球の体積\(\,V_1\,\)は
　\(\hspace{4pt}\displaystyle \color{red}{V_1}=\color{red}{\frac{4\,\pi\,r^3}{3}}\)
円柱の体積\(\,V_2\,\)は
　\(\begin{eqnarray}
\color{blue}{V_2}&=&\pi\,r^2\times 2\,r\\
&=&\color{blue}{2\,\pi\,r^3}
\end{eqnarray}\)
よって球の体積は円柱の体積の
　\(\begin{eqnarray}
\color{red}{V_1}\div \color{blue}{V_2}&=&\color{red}{\frac{4\,\pi\,r^3}{3}} \div \color{blue}{2\,\pi\,r^3}\\
&=&\frac{4}{3}\div 2\\
&=&\frac{4}{3}\times \frac{1}{2}\\
&=&\underline{\underline{　\frac{2}{3}　}}\,(\,倍\,)
\end{eqnarray}\)

長さは与えられていないので好きな長さで計算しても比は同じです。
（例えば球の半径を\(\,3\,\)とする、など）

(7)
動点と確率です。

条件から２つのさいころの出た目の和は、
\(\,2\,\)以上\(\,12\,\)以下になるので和が
　\(\hspace{4pt}3\,,\,7\,,\,11\)
のときに点\(\,\mathrm{D}\,\)に移動することが分かれば答えが出ます。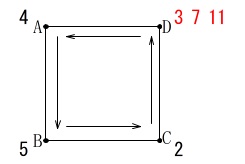樹形図で良いですが、さいころ２つなので表で見ます。
　\(\begin{array}{|c|c|c|c|c|c|c|} \hline
& \,1\, & \,2\, & \,3\, & \,4\, & \,5\, & \,6\, \\ \hline
\,1\, & & ○ & & & & ○\\ \hline
2 & ○ & & & & ○ & \\ \hline
3 & & & & ○ & & \\ \hline
4 & & & ○ & & & \\ \hline
5 & & ○ & & & & ○ \\ \hline
6 & ○ & & & & ○ & \\ \hline
\end{array}\)

答え　\(\displaystyle \frac{10}{36}=\underline{\underline{　\frac{5}{18}　}}\)

(8)
作図です。

\(\,\mathrm{∠APC}=45°\,\)なので直角二等辺三角形を作れば良いだけです。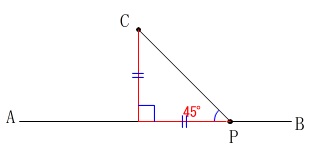先ず\(\,\mathrm{C}\,\)から\(\,\mathrm{AB}\,\)に垂線を下ろします。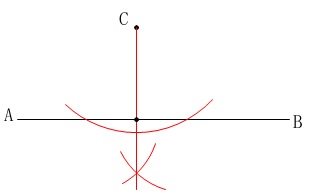\(\,\mathrm{AB}\,\)との交点から\(\,\mathrm{C}\,\)までの長さを\(\,\mathrm{B}\,\)側にとれば終わりです。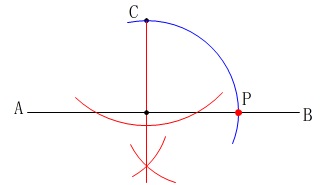\(\,45°\,\)は\(\,90°\,\)の二等分線で作れますが、
正方形の対角線でも作れるので覚えておきましょう。

⇒　作図問題の解き方と入試問題(角の二等分線･垂線･円の接線他)

大まかにですが作図のポイントをまとめてありますので参考にして下さい。
（会員の方はオリジナル作図問題集『さくっと！』を何度も読み返して必ず得点しましょう。）

第２問

\(\color{black}{\fbox{\(\,\large{2}\,\)}}\)
一次関数の問題ですが日本語が長いです。

簡単にまとめると、同時に使うことはなく
　\(\,\mathrm{A}\,\)：毎分\(\,\mathrm{\color{red}{12}\,cm}\,\)
　\(\,\mathrm{B}\,\)：毎分\(\,\mathrm{\color{blue}{6}\,cm}\,\)
　\(\,\mathrm{C}\,\)：毎分\(\,\mathrm{\color{magenta}{2}\,cm}\,\)
で水が入る。

(1)
①
連立方程式を立てます。

\(\,\mathrm{A}\,\)を\(\,a\,\)分、\(\,\mathrm{B}\,\)を\(\,b\,\)分合わせて６分使って,
\(\,\mathrm{50\,cm}\,\)入れる。

先ず時間の関係式は
　\(\hspace{4pt}a+b=6\)
水が毎分入る高さは\(\,\mathrm{A\,,\,B}\,\)それぞれ一定なので
　\(\hspace{4pt}\color{black}{\fbox{\(\,\color{red}{12}a+\color{blue}{6}b\,\)}}=50\)

②
問題にある図２の読み取りです。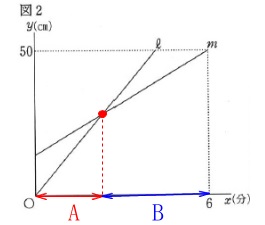それぞれの直線の傾きは、
　「１分間あたりに高くなる水面の高さ」
交点は\(\,\mathrm{A}\,\)と\(\,\mathrm{B}\,\)を替えたところです。
つまりは交点の\(\,x\,\)座標は
　「給水管\(\,\mathrm{A}\,\)の使用時間」
を表しています。

答え　\(\,\underline{　ウ　}\,\)

(2)
今度は\(\,\mathrm{45cm}\,\)の高さになるまでを考えます。

使う順序は\(\,\mathrm{A\,,\,B}\,\)または\(\,\mathrm{A\,,\,C}\,\)です。

①
６分で\(\,\mathrm{45cm}\,\)の高さまで水を入れますが、
１分間に入る水の量は同じなので傾きは同じです。
　「直線\(\,m\,\)に平行で\(\,(6\,,\,45\,)\,\)を通る直線」
または
　「\(\,y\,\)軸方向に\(\,-5\,\)だけ平行移動した直線」
だけど『平行移動』は使うか悩みますね。
（『正答』で使っているので良いのでしょう。）
※
平行移動を使う場合は移動分を『だけ』を使って表すので注意。

②
水の入る量が毎分\(\,\mathrm{2\,cm}\,\)なので、
\(\,\mathrm{C}\,\)を表す直線は傾きは小さいです。

図２では\(\,6\,\)分後\(\,\mathrm{50cm}\,\)ですが、
\(\,6\,\)分後\(\,\mathrm{45cm}\,\)なので6分後の水の高さを見れば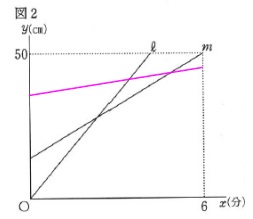おおよそのグラフは分かりますね。

答え　\(\,\underline{　エ　}\,\)

(3)
今度は\(\,\mathrm{B\,,\,A\,,\,C}\,\)の順に使い高さ\(\,\mathrm{48\,cm}\,\)にします。

素直に関数として考えましょう。

\(\,\mathrm{B}\,\)の傾きは\(\,6\,\)なので、
入れはじめてからの関数は
　\(\hspace{4pt}y=6\,x\)
\(\,1\,\)分後には\(\,y=\,6\,\)になっています。
　\(\hspace{4pt}(\,1\,,\,6\,)\)
を通る直線です。
\(\,\mathrm{C}\,\)の傾きは\(\,2\,\)で\(\,6\,\)分後に\(\,48\,\)になっているので
傾き\(\,2\,\)で\(\,(\,6\,,\,48\,)\,\)を通る直線は
　\(\hspace{4pt}y=2\,x+36\)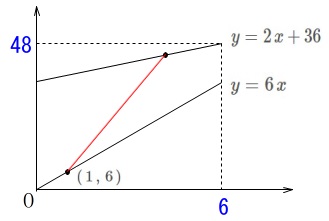\(\,\mathrm{B}\,\)と\(\,\mathrm{C}\,\)の間を\(\,\mathrm{A}\,\)がつなぎます。
（入れはじめて１分後からです。）

\(\,\mathrm{A}\,\)の傾きは\(\,12\,\)で\(\,(\,1\,,\,6\,)\,\)を通るので
\(\,\mathrm{A}\,\)を表す赤線の直線は
　\(\hspace{4pt}y=12\,x-6\)

\(\,\mathrm{C}\,\)に変更するのは交点の\(\,x\,\)座標で見れば良いので連立します。
　\(\begin{eqnarray}\displaystyle
12\,x-6&=&2\,x+36\\
10\,x&=&42\\
x&=&4+\frac{1}{5}\,(\,分\,)
\end{eqnarray}\)

答え　\(\underline{　4　}分\underline{　12　}秒後\)

\(\displaystyle \,\frac{1}{5}\,(\,分\,)=\frac{1}{5}\times 60=12\,(\,秒\,)\)です。

日本語の文字数いくらあるんだろうか。
どこもかしこも会話調の問題が多い。
読み取る力を見るのは良いですが、
いい加減にやめて欲しい。笑

次は関数問題で図形との融合ですがシンプルです。

第３問

\(\color{black}{\fbox{\(\,\large{3}\,\)}}\)
双曲線と点の座標が与えられています。
条件
　関数：\(\displaystyle \,y=\frac{6}{x}\,\)
　点\(\,\mathrm{A}\,\)：\(\,(\,-6\,,\,-1\,)\,\)
　点\(\,\mathrm{B}\,\)：\(\,(\,-3\,,\,-5\,)\,\)
点\(\,\mathrm{A}\,\)は双曲線上の点です。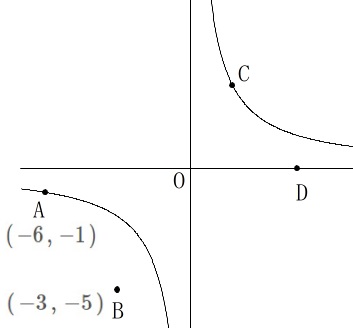点\(\,\mathrm{C}\,\)は双曲線上の\(\,x\,\)座標が正の点、
点\(\,\mathrm{D}\,\)は\(\,x\,\)座標が正の\(\,x\,\)軸上の点です。

問題は簡単なので先に進みましょう。

(1)
点\(\,\mathrm{C}\,\)の\(\,x\,\)座標が\(\,1\,\)のとき
　\(\begin{eqnarray}
y&=&\frac{6}{1}\\
&=&\underline{　6　}
\end{eqnarray}\)

(2)
2点\(\,\mathrm{C\,,\,D}\,\)が\(\,\mathrm{ＯＣ＝ＣＤ}\,\)を保ちながら動くとき、
\(\,\mathrm{△OCD}\,\)の面積はどう変化するかです。

条件から\(\,\mathrm{△OCD}\,\)の面積は
　底辺\(\,\mathrm{OD}\,\)、高さ\(\,\mathrm{C}\,\)の\(\,y\,\)座標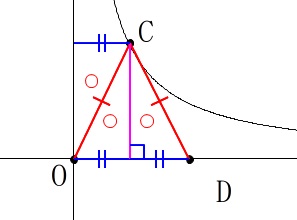なので\(\,\mathrm{△OCD}\,\)が二等辺三角形であることから、
点\(\,\mathrm{C}\,\)から\(\,x\,\)軸におろした垂線で２等分されます。

このことから\(\,\mathrm{△OCD}\,\)の面積は、
\(\,\mathrm{OC}\,\)を対角線とする長方形と同じ面積だという事も確認できます。

関数\(\displaystyle \,y=\frac{6}{x}\,\)は
　\(\hspace{4pt}x\,y=6\)
となることから\(\,x\,\)座標と\(\,y\,\)座標の積は常に一定です。
（底辺と高さの積が一定と見ることができる。）

つまり\(\,\mathrm{△OCD}\,\)の面積は　「一定である。」

答え　\(\,\underline{　オ　}\,\)

⇒　比例と反比例のグラフから三角形,四角形の面積を求める問題の解き方

これはよく使う事実なので覚えておくと良いです。

(3)
面積が等しくなるように点\(\,\mathrm{D}\,\)の\(\,x\,\)座標を求めます。
　\(\hspace{4pt}\mathrm{△OAB\,=\,△OBD}\)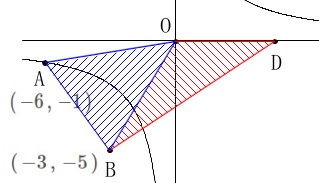方針は単純に見れば2つあります。

(3)具体的な面積を利用する方法

１つは\(\,\mathrm{A\,,\,B}\,\)が定点で\(\,\mathrm{△OAB}\,\)は定まるので、
点\(\,\mathrm{D}\,\)の\(\,x\,\)座標を設定し求める方法です。

\(\,\mathrm{△OAB}\,\)の面積は長方形から三角形３つ引けば出てきます。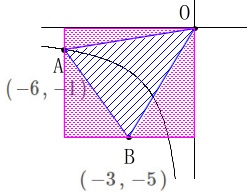面積計算は長方形の縦、横の長さを\(\,x\,\)座標、\(\,y\,\)座標から求めて見て下さい。
　\(\hspace{4pt}\displaystyle \mathrm{\color{red}{△OAB}}=\color{red}{\frac{27}{2}}\)
※
会員にはおなじみなので公式カード使って\(\,10\,\)秒もあれば求まるでしょう。

また、点\(\,\mathrm{D}\,\)の\(\,x\,\)座標を\(\,\color{red}{t}\,\)とすると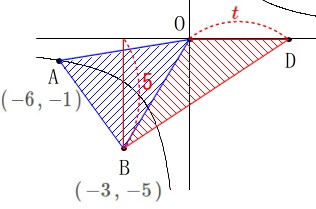
\(\,\mathrm{△OBD}\,\)の面積は底辺\(\,\mathrm{OD}\,\)、
高さは\(\,\mathrm{B}\,\)の\(\,y\,\)座標の絶対値になるので\(\,\color{red}{5}\,\)だから
　\(\begin{eqnarray}
\mathrm{\color{blue}{△OBD}}&=&\frac{1}{2}\times t\times 5\\
&=&\color{blue}{\frac{5}{2}\,t}
\end{eqnarray}\)

よって\(\,\mathrm{△OAB=△OBD}\,\)となるとき
　\(\begin{eqnarray}
\color{red}{\frac{27}{2}}&=&\color{blue}{\frac{5}{2}\,t}\\
t&=&\underline{\underline{　\frac{27}{5}　}}
\end{eqnarray}\)

(3)平行線を利用する方法

もう一つは\(\,\mathrm{OB}\,\)を共通の底辺とみて、
平行線で高さを同じにします。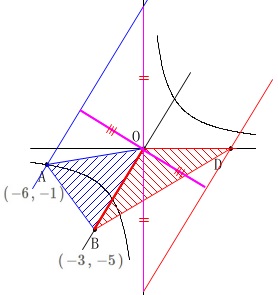　直線\(\,\mathrm{BO}\,\)は\(\displaystyle \,y=\frac{5}{3}\,x\,\)
直線\(\,\mathrm{A}\,\)を通る平行線は\(\,(\,-6\,,\,-1\,)\,\)を通るので
　\(\hspace{4pt}\displaystyle y=\frac{5}{3}\,x+9\)
このことから\(\,y\,\)切片を考えると点\(\,\mathrm{D}\,\)を通る平行線は
　\(\displaystyle \hspace{4pt}y=\frac{5}{3}\,x-9\)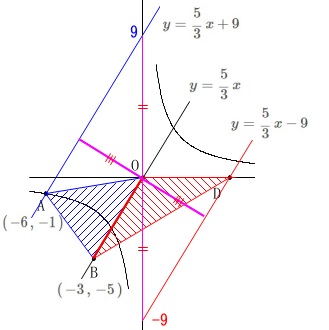これが\(\,x\,\)軸と交わるのは\(\,y=0\,\)のときなので
　\(\begin{eqnarray}\displaystyle
\frac{5}{3}\,x-9&=&0\\
x&=&\underline{\underline{　\frac{27}{5}　}}
\end{eqnarray}\)
とすることもできます。

(4)
四角形\(\,\mathrm{ABDC}\,\)が平行四辺形になるとき、
直線\(\,\mathrm{BD}\,\)の式を求めます。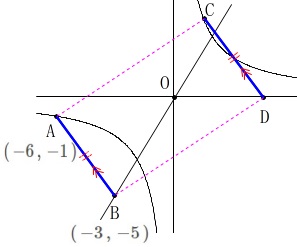平行四辺形になるには、
対辺が等しく、平行になれば良いので、
点\(\,\mathrm{D}\,\)の座標を\(\,(\,t\,,\,0\,)\,\)とすると、
２点\(\,\mathrm{A\,,\,B}\,\)の\(\,x\,\)座標、\(\,y\,\)座標の増減から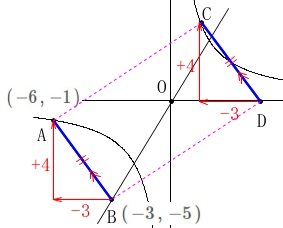点\(\,\mathrm{C}\,\)の座標は\(\,(\,t-3\,,\,4\,)\)となり、
これが双曲線上の点になるので\(\,\displaystyle y=\frac{6}{x}\,\)に代入して
　\(\begin{eqnarray}
4&=&\frac{6}{t-3}\\
4(t-3)&=&6\\
4t&=&18\\
t&=&\frac{9}{2}
\end{eqnarray}\)
このとき点\(\,\mathrm{D}\,\)の座標は
　\(\hspace{4pt}\displaystyle \left(\,\frac{9}{2}\,,\,0\,\right)\)

よって２点\(\,\mathrm{B\,,\,D}\,\)を通る直線の式は
　\(\hspace{4pt}\displaystyle \underline{\underline{　y=\frac{2}{3}\,x-3　}}\)

⇒　変化の割合とは？1次関数の求め方と直線の方程式との違い

直線の式の中でも２点を通る直線の式は、
素早く求められるようになっておくと良いですよ。
何が良いか？
時間をかせいで問題を読む時間が増えます。

第４問

\(\color{black}{\fbox{\(\,\large{4}\,\)}}\)
円と内接する三角形、四角形の問題です。

各点は図の通りですが条件を簡単にまとめておきます。
条件
　\(\hspace{4pt}\mathrm{AB=AD}\)
　\(\,\mathrm{AG}\,\)∥\(\,\mathrm{BC}\,\)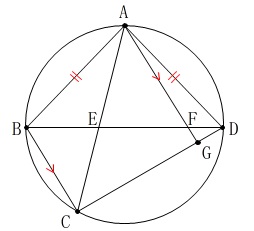相似な図形がたくさんありますが、
線分\(\,\mathrm{BD}\,\)は直径ではないので注意が必要です。

(1)
問題
「\(\,\mathrm{∠ABD}=a^{\circ}\,\)とするとき、\(\,\mathrm{∠BCD}\,\)の大きさを\(\,a\,\)を用いて表せ。」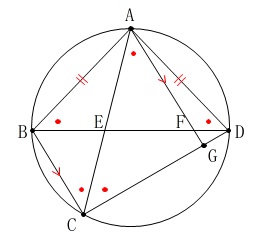条件から、
円周角の定理と平行線の錯角が等しくなるので、
（二等辺三角形\(\,\mathrm{ABD}\,\)の底角もあります。）
図の赤丸\(\,\color{red}{・}\,\)の角度は等しくなります。
２つ分あるので
　\(\begin{eqnarray}\displaystyle
\mathrm{∠BCD}&=&2\times \mathrm{∠ABD}\\
&=&\underline{　2\,a^{\circ}　}
\end{eqnarray}\)

(2)
相似の証明です。
　\(\,\mathrm{△AEF}\,\)∽\(\,\mathrm{△CEB}\,\)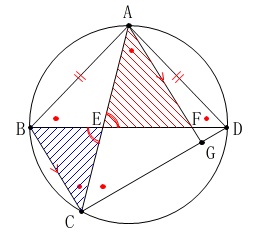平行線の錯角と対頂角で２角が等しいことが分かります。

⇒　中学の図形証明問題(合同･相似)の解き方と証明の書き方ポイント

相似条件
　「２組の角がそれぞれ等しい。」
がそろえば良いので書き方は自由にして下さい。

(3)
長さの条件が加わります。
　\(\hspace{4pt}\mathrm{AB}=6\,,\,\mathrm{BC}=4\,,\,\mathrm{AC}=8\)※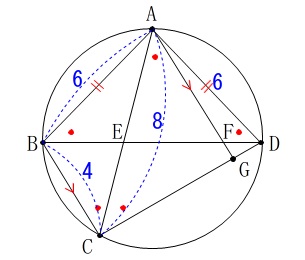
長さの単位は\(\,\mathrm{cm}\,\)です。
①
問題
「\(\,\mathrm{△ABE}\,\)の面積は\(\,\mathrm{△BCE}\,\)の面積の何倍か。」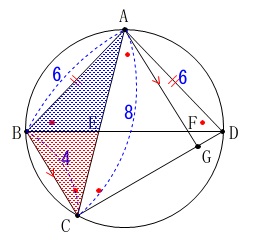高さが共通なので、
底辺となる\(\,\mathrm{AE}\,\)と\(\,\mathrm{CE}\,\)の線分比を出せば良いです。

(2)の相似の利用を考えましたが遠いような気がするので、
　\(\,\mathrm{△ABC}\,\)∽\(\,\mathrm{△AEB}\,\)
を利用します。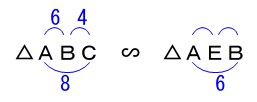※どの相似が使えるかは、
ボーとながめててもなかなか見つかりません。
できる限り相似を書き出してどれが使えそうか試すしかありませんよ。
（少なくとも才能のない私はそうします。）

相似比から
　\(\begin{eqnarray}\displaystyle
\mathrm{AB:AC}&=&\mathrm{AE:AB}\\
6:8&=&\mathrm{AE}:6\\
8\times \mathrm{AE}&=&6\times 6\\
\mathrm{AE}&=&\color{magenta}{\frac{9}{2}}
\end{eqnarray}\)
このとき
　\(\begin{eqnarray}\displaystyle
\mathrm{EC}&=&\mathrm{AC-AE}\\
&=&\color{blue}{8}-\color{magenta}{\frac{9}{2}}\\
&=&\color{magenta}{\frac{7}{2}}
\end{eqnarray}\)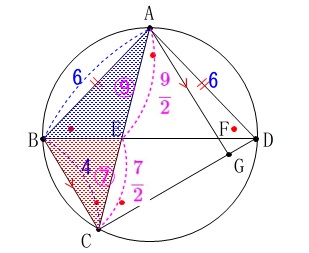つまり、
　\(\hspace{4pt}\mathrm{AE:EC}=9:7\)
よって、
　\(\begin{eqnarray}
\mathrm{△ABE:△BCE}&=&9:7\\
\mathrm{△ABE}&=&\frac{9}{7}\times \mathrm{△BCE}
\end{eqnarray}\)

答え　\(\displaystyle \underline{\underline{　\frac{9}{7}　}}\,(\,倍\,)\)

辺の長さのままから
　\(\hspace{4pt}\displaystyle \color{magenta}{\frac{9}{2}}\div \color{magenta}{\frac{7}{2}}=\frac{9}{2}\times \frac{7}{2}=\frac{9}{7}\)
としても良いです。

分数になると比の出し方がわかりにくいという人がいますが、
「\(\,10\,\)は\(\,5\,\)の何倍か？」
というときの計算順序と同じにすれば良いだけです。

②
問題
「線分\(\,\mathrm{AG}\,\)の長さを求めよ。」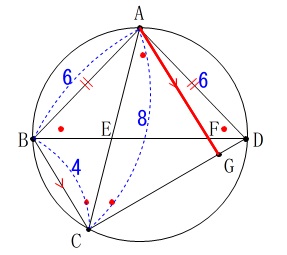これも(2)や(3)の①からの誘導か、
それとも三平方の定理か悩みそうです。

ただ、平行線はあるけど垂線は見当たらないので、
三平方の定理ではなく相似で探すと
　\(\,\mathrm{△ABD}\,\)　∽　\(\,\mathrm{△GAC}\,\)
がありました。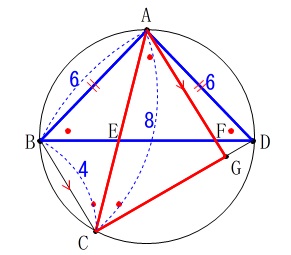長さがある三角形どうしなのでなんとかなりそうです。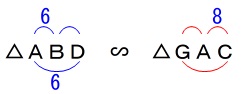ここで、
「あれ？線分\(\,\mathrm{BD}\,\)の長さを出していない。」
と気がつきました。
※
本当なら(2)と(3)の①が求まったときに出しておくところです。もう一度戻ると、
　\(\begin{eqnarray}
\mathrm{AC:AB}&=&4:\mathrm{EB}\\
8:6&=&4:\mathrm{EB}\\
\mathrm{EB}&=&\color{magenta}{3}
\end{eqnarray}\)

線分\(\,\mathrm{DE}\,\)が欲しいのでもう一つ相似を使います。
　\(\,\mathrm{△EBD}\,\)∽\(\,\mathrm{△EAD}\,\)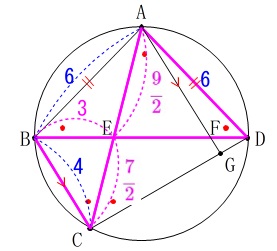比例式を解くのは飽きたので自分でやってみて下さい。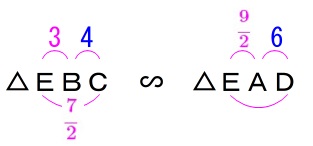比例式を解くと
　\(\hspace{4pt}\displaystyle \mathrm{DE}=\color{red}{\frac{21}{4}}\)
これらのことから（遠回りしてしまいましたが）
　\(\begin{eqnarray}\displaystyle
\mathrm{BD}&=&\mathrm{BE+DE}\\
&=&3+\frac{21}{4}\\
&=&\color{red}{\frac{33}{4}}
\end{eqnarray}\)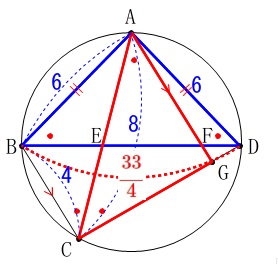再び元にもどします。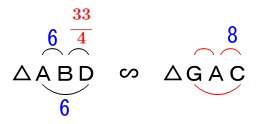
　\(\begin{eqnarray}\displaystyle
\mathrm{BA:AG}&=&\mathrm{BD:AC}\\
6:\mathrm{AG}&=&\frac{33}{4}:8\\
\frac{33}{4}\times \mathrm{AG}&=&6\times 8\\
\mathrm{AG}&=&\frac{4}{33}\times 6\times 8\\
&=&\underline{\underline{　\frac{64}{11}　}}\,(\,\mathrm{cm}\,)
\end{eqnarray}\)