2023年(令和5年)度北海道公立高校入試問題の数学の問題と解説

2023年(令和5年)度北海道公立高校入試問題の数学の問題と解説です。
難問というほどの難問はありませんが、
簡単な整数問題もあり数学の総合的な知識を問われます。
問題の読み取りと理由、説明の書き方で日本語の力もある程度必要になっていますので、
数学の基本知識は確実にしておくことがポイントです。

※
このページは対策するところではないのですが、
学校裁量問題はなくなり共通問題なので傾向を探れる過去問としては昨年度だけです。
全体で高得点を狙うなら数年前からの学校裁量問題にも目を通しておいた方が良いですね。
ただし、多少違いがあるので対策は各々にお任せします。

2023年(令和5年)度北海道公立高校入試問題の数学の問題

令和５年度北海道の公立高校入試の数学問題です。

⇒　令和５年度北海道の公立高校入試の数学問題ＰＤＦ

大問\(\color{black}{\fbox{1}}\)から\(\color{black}{\fbox{5}}\)まであります。
１０ページありますので国語の問題並みだと思っていて良いです。

2023年(令和5年)度北海道公立高校入試問題の数学の解説

日本語の文字数は多いですが数学の問題としてはそれ程ややこしいわけではありません。
読み取り、説明の日本語の力で差がつくので、
自分で考えたことを数式ではなく日本語で表現する練習をしておくと良いかもしれません。
（私は苦手なので国語の先生に相談して下さい。）

数学のポイントの解説をはじめます。

第１問

\(\color{black}{\fbox{1}}\)
問１は計算問題です。
(1)
　\(\hspace{10pt}9-(-5)\\
=9+5\\
=\underline{　14　}\)

「負の数を引く」のは「正の数を足す」ことになります。
（数直線で考えると良いです。）

(2)
　\(\hspace{10pt}\displaystyle (-3)^2\div \frac{1}{6}\\
\displaystyle =9\times 6\\
=\underline{　54　}\)

計算順序の確認ですね。
割り算は逆数の掛け算とすると処理が速いです。

(3)
　\(\hspace{10pt}\sqrt{2}\times \sqrt{14}\\
=\sqrt{28}\\
=\underline{　2\sqrt{7}　}\)

無理数の計算は慣れ具合によりますが、
暗算は避けて確実に素因数分解しましょう。
　\(\hspace{10pt}\sqrt{2}\times \sqrt{14}\\
=\sqrt{2}\times \sqrt{2}\times \sqrt{7}\\
=\underline{　2\sqrt{7}　}\)
としても良いです。

問２は確率です。

くじを引くのは\(\,\mathrm{A}\,\)さんだけと考えても良いですが、
何番目にくじを引くかは関係ありません。
１から９までのくじの中に偶数は４つあるので
　\(\hspace{10pt}\displaystyle \underline{\underline{　\frac{4}{9}　}}\)

何番目にくじを引いても確率は同じです。

問３は１次関数の問題です。

１次関数は２点が分かれば関数が決まります。
　\(\hspace{4pt}(\,-1\,,\,6\,)\)
　\(\hspace{4pt}(\,3\,,\,2\,)\)
変化の割合（傾き\(\,a\,\)）は
　\(\begin{eqnarray}
a&=&\frac{　(y\,の増分)　}{　(x\,の増分)　}\\
&=&\frac{2-6}{3-(-1)}\\
&=&-1
\end{eqnarray}\)
なので関数は
　\(\hspace{10pt}y=-x+5\)
\(\,x=0\,\)のとき、
　\(\hspace{10pt}y=-(0)+5=\underline{　5　}\)

関数を出さなくても傾きが\(\,-1\,\)と分かれば
\(\,x\,\)の増分が\(\,1\,\)なら\(\,y\,\)の増分が\(\,-1\,\)なので
\(\,x=-1\,\)のときより\(\,y\,\)は\(\,-1\,\)増えるので
　\(\hspace{10pt}6+(-1)=\underline{　5　}\)
としても同じです。

一次関数と問題に書いてるので、
関数を求めておくことを優先すれば問題ありません。
　
問４円錐（円すい）の問題です。

底面の半径が分かっているので底面積は分かります。
　底面の半径：\(\,r=\color{red}{6}\,\)\(\,\mathrm{cm}\,\)
　円錐の体積：\(\,V=\color{red}{132\,\pi}\,\mathrm{cm^3}\,\)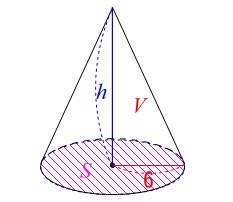

底面積\(\,\color{magenta}{S}\,\)は
　\(\hspace{10pt}\color{magenta}{S}=\pi\,r^2=\color{magenta}{36\,\pi}\)
体積が与えられているので高さを\(\,h\,\)として方程式にします。
　\(\begin{eqnarray}
\color{red}{V}&=&\frac{1}{3}\times \color{magenta}{S}\times \color{blue}{h}\\
132\,\pi&=&\frac{1}{3}\times 36\,\pi\times h\\
h&=&\underline{　11　}\mathrm{cm}
\end{eqnarray}\)

問\(\,5\,\)２次方程式の解と係数の関係です。
　\(\hspace{10pt}x^2-\color{black}{\fbox{　\(\,\color{red}{k}\,\)　}}\,x+14=(x-a)(x-b)\)

方程式でないと思うかもしれませんが、
左辺が右辺のように因数分解できるということは、
\(\,(\,左辺\,)=0\,\)の２次方程式の解が\(\,a\,,\,b\,\)ということです。

「自然数」なので正の整数だけを見れば良いので答えは出るでしょう。
定数項に注目すると１４なので
　\(\hspace{4pt}a\,b=1\times 14\,,\,2\times 7\)
が考えられます。
　\(\hspace{4pt}(x-1)(x-14)=x^2-\underline{　15　}x+14\)
　\(\hspace{4pt}(x-2)(x-7)=x^2-\underline{　9　}x+14\)

問題の答えとなる２つの『自然数』は解ではなく「係数」なので間違えないで下さい。

上の方程式の右辺を展開すると
　\(\hspace{4pt}x^2-k\,x+14=x^2-(a+b)\,x+a\,b\)
係数比較することで
　\( \begin{cases}
\hspace{4pt} a+b&=&k\\
\hspace{4pt} 　a\,b&=&14
\end{cases}\)
という条件が出てきますが連立しても求められません。

難しく考えなくて良いです。
ここでは定数項に着目することと、
自然数という条件から展開して\(\,k\,\)を求める問題です。

問６
作図ですが条件が与えられているので図示しておきます。
条件
　\(\hspace{4pt}\mathrm{∠ACB}=75^{\circ}\)
　\(\hspace{4pt}\mathrm{BA=BC}\)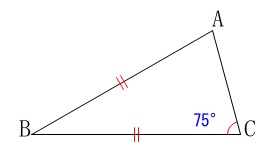この条件において
　\(\hspace{4pt}\mathrm{∠PBC=∠PCB}=15^{\circ}\)
となる点\(\,\mathrm{P}\,\)を作図します。
（\(\,\mathrm{∠PBC=∠PBA}\,\)ではないので間違えないように。）

「\(\,15°\,\)はどこから？」
と思うでしょうが二等辺三角形という条件が与えられているので、
頂角が\(\,30°\,\)だと気がつくのは容易でしょう。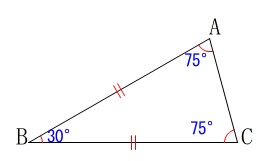頂角の二等分線上の点なら\(\,\mathrm{∠PBC=15°}\,\)を満たします。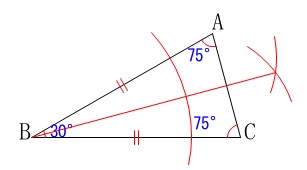もう一つの\(\,\mathrm{∠PCB=15°}\,\)は、
\(\,\mathrm{△PBC}\,\)が二等辺三角形となれば良いので線分\(\,\mathrm{BC}\,\)の垂直二等分線を引けば終わりです。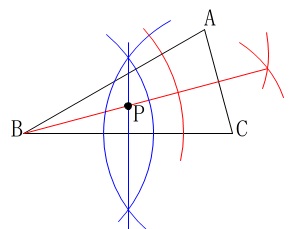作図の基本手法だけで終わりますので確実に取りましょう。
オリジナル作図問題集『さくっと！』で鍛えた会員は物足りないかもしれないけど、
この基本になる定理は忘れてはいけませんよ。

第２問

\(\color{black}{\fbox{2}}\)
かけ算九九の表を利用した文字式の問題です。

問題文の意味はわかると思うので解説のみとします。

問１
（予想\(\,\mathrm{Ⅰ}\,\)）が正しいとはいえないことを説明します。
　（予想\(\,\mathrm{Ⅰ}\,\)）
\(\color{black}{\fbox{縦横に隣り合う４つの数の和は、５の倍数である。}}\)

正しくないではありません。
「正しいとはいえない」というのは正しくない場合もある、という意味です。

探せばいいですよ。
答えはたくさんありますが小さい方が楽でしょう。
一番左上の４つを見ると
　\(\,a=\underline{　1　}\,,\,b=\underline{　2　}\,,\,c=\underline{　2　}\,,\,d=\underline{　4　}\)
これらの和は
　\(\hspace{4pt}1+2+2+4=\underline{　9　}\)
で\(\,5\,\)の倍数になっていません。

一番右下でもいいです。
　\(\,a=\underline{　64　}\,,\,b=\underline{　72　}\,,\,c=\underline{　72　}\,,\,d=\underline{　81　}\)
これらの和は
　\(\hspace{4pt}1+2+2+4=\underline{　289　}\)
で\(\,5\,\)の倍数になっていません。
\(\,5\,\)の倍数になっていなければどれでも良いです。
（割と多いので適当に選んでも当たりますが足し算を間違えないように。）

問２
（予想\(\,\mathrm{Ⅱ}\,\)）がいつも成り立つことを説明します。
　（予想\(\,\mathrm{Ⅱ}\,\)）
前半は予想\(\,\mathrm{Ⅰ}\,\)と同じで、４つの数の和は
　\(\color{black}{\fbox{（かけられる数の和）×（かける数の和）である。}}\)

足す４つの数は\(\,a\,,\,b\,,\,c\,,\,d\,\)ですが、
かけるのはそのものではないので意味が取りにくいです。

そこで（説明）の中でヒントがあります。
　「かけられる数\(\,m\,\)、かける数\(\,n\,\)の積を\(\,a\,\)とする。」
　\(\hspace{4pt}a=m\,n\)

\(\,b\,\)は\(\,a\,\)より「かける数」が\(\,1\,\)大きくなるので
（「かけられる数」は同じ）
　\(\hspace{4pt}b=\color{black}{\fbox{\(\,m(n+1)\,\)}}\)
同じように見ていけば
　\(\hspace{4pt}c=\color{black}{\fbox{\(\,(m+1)n\,\)}}\)
　\(\hspace{4pt}d=\color{black}{\fbox{\(\,(m+1)(n+1)\,\)}}\)

このとき
　\(\begin{eqnarray}
a+b+c+d&=&mn+m(n+1)+(m+1)n+(m+1)(n+1)\\
&=&4mn+2n+2n+1\\
&=&(2m+1)(2n+1)\\
&=&\{\color{black}{\fbox{\(\,m+(m+1)\,\)}}\}\{\color{black}{\fbox{\(\,n+(n+1)\,\)}}\}
\end{eqnarray}\)

ここの変形は強引に見えますが、
（説明）の結論部分につながるようにするためです。
（問題の（予想\(\,\mathrm{Ⅱ}\,\)）の形。）

問３
優さんは６つの数字の和において
　\(\color{black}{\fbox{（かけられる数の和）×（かける数の和）}}\)
となることが分かりました。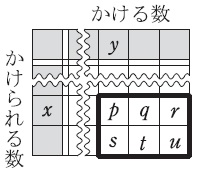
このとき
　\(\hspace{4pt}p+q+r+s+t+u=162\)
となる\(\,x\,,\,y\,\)を求めます。

\(\,x\,,\,y\,\)は「かけられる数」と「かける数」です。
問１問２からの流れから
　\(\hspace{4pt}q=x(y+1)\)
　\(\hspace{4pt}s=(x+1)y\)
　\(\hspace{4pt}\vdots\)
などと表すのも良いですね。

ただ、６つの数の和は
　\(\color{black}{\fbox{（かけられる数の和）×（かける数の和）}}\)
となることが分かっています。
　\(\hspace{10pt}p+q+r+s+t+u\\
=\{\,x+(x+1)\,\}\{\,y+(y+1)+(y+2)\,\}\\
=(2x+1)(3y+3)\)
となるので
　\(\begin{eqnarray}\displaystyle
(2x+1)(3y+3)&=&162\\
(2x+1)(y+1)&=&54
\end{eqnarray}\)
となる自然数\(\,x\,,\,y\,\)を求めれば良いことになります。

自然数の積が\(\,54\,\)になる組み合わせは
　\(\color{black}{\fbox{\(\,1\times 54\,\)}}\)
　\(\color{black}{\fbox{\(\,2\times 27\,\)}}\)
　\(\color{black}{\fbox{\(\,3\times 18\,\)}}\)
　\(\color{black}{\fbox{\(\,6\times 9\,\)}}\)
この中で条件を満たすのは\(\,2x+1\,\)が奇数であることと、
\(\,x\,,\,y\,\)が自然数であることから調べて行くと
　\(\hspace{10pt}2x+1=9\,,\,y+1=6\)
が分かります。

答え　\(\,x=\underline{　4　}\,,\,y=\underline{　5　}\,\)

この問題優「くん」は次のように答えを見つけました。
　\(\hspace{10pt}162\div 6=27\)
となるのでその前後の６つの数の和になっているはず、
ということで和の一の位が\(\,2\,\)になるところを探すと
　\(\hspace{10pt}20+24+28+24+30+36=162\)

これから答えの候補が見つけることができました。
（いざとなればこれを答えにするのは優「くん」だけで良いです。）
　\(\color{black}{\fbox{（かけられる数の和）×（かける数の和）}}\)
問題の流れからこの条件を利用できるようになっておきましょう。

第３問

\(\color{black}{\fbox{3}}\)
関数です。

固定されている関数は１つだけです。
　\(\hspace{4pt}y=ax^2　(\,a\,＞\,0\,)　･･･①\)
　\(\hspace{4pt}y=-3x^2　･･･②\)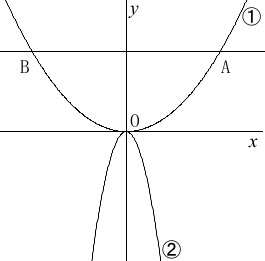後の条件は問ごとに違ってくるので注意しましょう。

問１
関数\(\,①\,\)の比例定数が\(\,a=2\,\)のときです。
　\(\hspace{4pt}y=2\,x^2　･･･①\)

点\(\,\mathrm{A}\,\)の\(\,y\,\)座標が\(\,8\,\)のとき点\(\,\mathrm{A}\,\)と点\(\,\mathrm{B}\,\)の距離、
つまり\(\,x\,\)座標の差（の絶対値）を求めます。
（点\(\,\mathrm{A}\,\)と点\(\,\mathrm{B}\,\)は\(\,x\,\)軸に平行なので\(\,y\,\)座標は同じです。）
　\(\begin{eqnarray}\displaystyle
8&=&2\times x^2\\
x&=&\pm 2
\end{eqnarray}\)
よって点\(\,\mathrm{A}\,\)と点\(\,\mathrm{B}\,\)の距離は
　\(\hspace{4pt}2-(-2)=4\)

答え　\(\,\underline{　4　}\,\)

イメージしにくい場合はグラフに座標を書き込んで確認して下さい。

問２
ここでは\(\,①\,\)の\(\,a\,\)は定まっていません。
　\(\hspace{4pt}y=a\,x^2　･･･①\)

\(\,①\,\)において\(\,x\,\)の値が\(\,1\,\)から\(\,3\,\)まで増加するときの変化の割合が、
一次関数\(\,y=x+2\,\)の変化の割合に等しいときの\(\,a\,\)の値を求めます。

\(\,①\,\)上の点は
　\(\hspace{4pt}(\,1\,,\,a\,)\)
　\(\hspace{4pt}(\,3\,,\,9\,a\,)\)
変化の割合は
　\(\hspace{4pt}\displaystyle \frac{9\,a-a}{3-1}=4a\)
よって、
　\(\begin{eqnarray}\displaystyle
4a&=&1\\
a&=&\underline{\underline{　\frac{1}{4}　}}
\end{eqnarray}\)
なぜ一次関数の\(\,x\,\)の値を無視しているかというと、
一次関数の変化の割合（傾き）は、
\(\,x\,\)の変化に関係なく一定で\(\,1\,\)だからです。

問３
ここでは\(\,①\,\)の比例定数と点\(\,\mathrm{A}\,\)が固定されます。
さらに条件が加わるのでまとめておきます。

\(\,①\,\)上の点\(\,\mathrm{A}\,\)の\(\,x\,\)座標が\(\,3\,\)、
\(\,②\,\)上の点\(\,\mathrm{C}\,\)の\(\,x\,\)座標が\(\,1\,\)なので
　\(\hspace{4pt}\displaystyle y=\frac{1}{3}\,x^2　･･･①\)
　\(\hspace{4pt}\displaystyle y=-3\,x^2　･･･②\)
　\(\,\mathrm{A\,(\,3\,,\,3\,)}\,,\,\mathrm{B\,(\,-3\,,\,3\,)}\,\)
　\(\,\mathrm{C\,(\,1\,,\,-3\,)}\,,\,\mathrm{D\,(\,-1\,,\,-3\,)}\,\)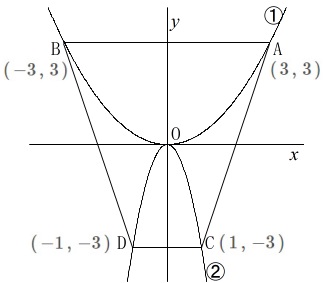ここまでは必ず書き出しましょう。
（もちろん後の点\(\,\mathrm{P\,,\,Q}\,\)もです。）

点\(\,\mathrm{P}\,\)は線分\(\,\mathrm{AB}\,\)上の点、点\(\,\mathrm{Q}\,\)は線分\(\,\mathrm{DC}\,\)上の点で、
点\(\,\mathrm{P}\,\)の\(\,x\,\)座標を\(\,t\,\)とします。
　\(\hspace{4pt}\mathrm{P}\,\color{red}{(\,t\,,\,3\,)}　(\,0\,＜\,t\,≦\,1\,)\)
問題は直線\(\,\mathrm{PQ}\,\)が原点\(\,\mathrm{O}\,\)を通るときです。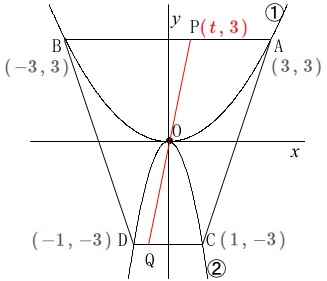(1)
点\(\,\mathrm{Q}\,\)の座標を求めます。

後のためにも点を設定しておきましょう。
線分\(\,\mathrm{AB}\,\)、\(\,\mathrm{DC}\,\)と\(\,y\,\)軸との交点をそれぞれ\(\,\mathrm{S\,,\,T}\,\)としておきます。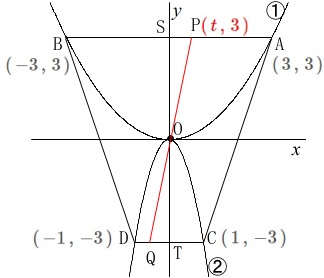２つの三角形は\(\,\mathrm{△OPS}\,\)≡\(\,\mathrm{△OQT}\,\)なので
点\(\,\mathrm{Q}\,\)の座標は点\(\,\mathrm{P}\,\)と原点対象です。

答え　\(\,\underline{　\mathrm{Q}\,(-t\,,\,-3\,)　}\,\)

(2)
直線\(\,\mathrm{PQ}\,\)が台形\(\,\mathrm{ABCD}\,\)を２等分することの説明です。台形\(\,\mathrm{ABCD}\,\)は固定されているので、
台形\(\,\mathrm{ABCD}\,\)の面積\(\,S\,\)は具体的に求まります。
　\(\begin{eqnarray}\displaystyle
S&=&\frac{6+2}{2}\times 6\\
&=&24
\end{eqnarray}\)

ここで\(\,\,0\,＜\,t\,≦\,1\,\,\)という条件の中でだけですが、
台形\(\,\mathrm{APQC}\,\)の面積\(\,S’\,\)は
　\(\hspace{4pt}\,\mathrm{CT}\,=1-(-t)=1+t\)
なの
　\(\begin{eqnarray}\displaystyle
S’&=&\frac{(3-t)+(1+t)}{2}\times 6\\
&=&12
\end{eqnarray}\)
よって、
　\(\hspace{4pt}\displaystyle S’=\frac{1}{2}\times S\)
（\(\,S=2S’\,\)でも良いです。）

これは直線\(\,\mathrm{PQ}\,\)が台形\(\,\mathrm{ABCD}\,\)を２等分することを意味しています。

図形的に見れば台形\(\,\mathrm{ABCD}\,\)の半分は台形\(\,\mathrm{ASTC}\,\)です。
（\(\,y\,\)軸が等脚台形の対称軸）
(1)で説明しているように\(\,\,\color{red}{0\,＜\,t\,≦\,1}\,\,\)という条件の中で、
\(\,\mathrm{△OPS}\,\)≡\(\,\mathrm{△OQT}\,\)なので、
（足し引きすれば\(\,0\,\)だから）
台形\(\,\mathrm{APQT}\,\)は台形\(\,\mathrm{ABCD}\,\)の半分だと直感的に分かります。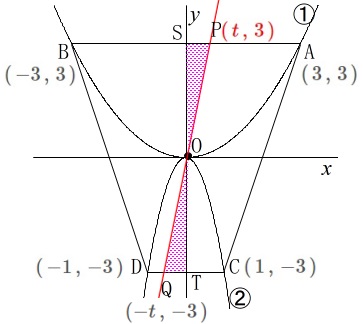いずれにしても、
　\(\,\,\color{red}{0\,＜\,t\,≦\,1}\,\,\)
という条件は問題にありますが解答上に示した方が良いです。

第４問

\(\color{black}{\fbox{4}}\)
平面図形です。

相似と合同だけなので簡単に済ませます。

問題全体で通じる条件があります。
条件
　直線\(\,\mathrm{AD}\,\)は\(\,\mathrm{∠BAC}\,\)の二等分線。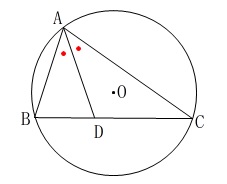こういった最初に与えられた条件は後半で忘れないようにしましょう。

問１
角度を求めますが条件が加わります。
　\(\,\mathrm{AD＝DC\,,\,∠BAD=35°}\,\)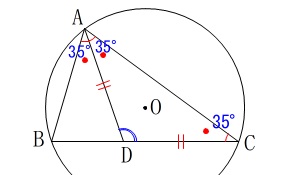この問の条件\(\,\mathrm{AD=DC}\,\)から\(\,\mathrm{△DAC}\,\)は二等辺三角形なので、
　\(\hspace{4pt}\mathrm{∠BAD=∠DAC=∠DCA}=\color{blue}{35^{\circ}}\)
すべての角度が固定されます。
　\(\hspace{10pt}\mathrm{∠ADC}=\underline{　110^{\circ}　}\)
（三角形の内角の和からで良いです。）

問２
相似の証明です。

円周角の定理から等しい角を示しておきます。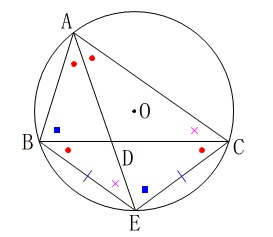最初の条件は変わっていませんよ。

(1)
２つの証明で言葉をそろえる必要があるので、
位置を確認しておいて下さい。
　ア　\(\,\underline{　弧\mathrm{AC}　}\,\)　イ　\(\,\underline{　円周角　}\,\)
相似条件はどちらも同じで
　ウ　\(\,\underline{　２組の角がそれぞれ等しい　}\,\)

アに入る言葉は円周角の定理のことなので
　\(\underline{　同一（長）の弧　}\)
でも良いような気はしますが具体的な弧で答えた方が無難ですね。

(2)
合同の証明です。
加わる条件は\(\,\mathrm{AB=AD}\,\)なので、
　\(\hspace{10pt}\,\mathrm{\color{blue}{∠ABD}=\color{blue}{∠ADB}}\,\)
また\(\,\mathrm{△CDE}\,\)は底角が等しく二等辺三角形になるので
　\(\hspace{10pt}\mathrm{DC=EC}\,,\,\mathrm{∠CDE=∠CED}\)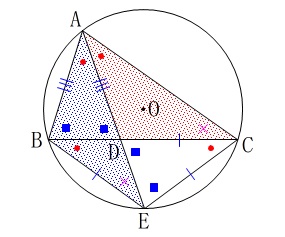対頂角は等しいので
　\(\hspace{10pt}\mathrm{\color{blue}{∠ADB}=\color{blue}{∠CDE}}\)
でもあります。

ここまで条件がそろえば合同の証明はどうでもなるでしょう。

⇒　中学２年平行と合同と証明の書き方ポイントまとめ

「ポイントまとめ」で確認して分かっているとは思いますが、
証明は図の中で終わらせておくことです。

合同条件は使う条件によって変わって良いです。
５つの合同条件のうち、
　「３組の辺がそれぞれ等しい。」\(\,\color{red}{※}\,\)
　「２組の辺とその間の角がそれぞれ等しい。」
　「１組の辺とその両端の角がそれぞれ等しい。」
の３つは使えるので自分の証明を信じて書き上げて下さい。
\(\,\color{red}{※}\,\)
図の中に書き込んでいませんが、（ごめんなさい。）
相似の証明をしているので\(\,\mathrm{AE=AC}\,\)も見つかるでしょう。

第５問

\(\color{black}{\fbox{5}}\)
データの問題で文字数が多いです。

こういう会話調の問題ではできるだけ必要な用語を追っていくと良いですよ。
（数学の問題として必要な用語に印をするなどしながら）

問１
２年分のデータの比較です。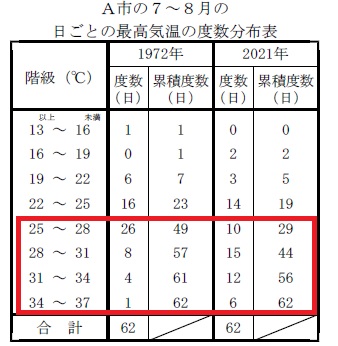夏日の度数は、（単純に度数を足して）
１９７２年が
　\(\hspace{10pt}26+8+4+1=\underline{　39　}\,(日)\)
２０２１年が
　\(\hspace{10pt}10+15+12+6=\underline{　43　}\,(日)\)
※
度数合計から\(\,25\,\)℃未満の度数を引いて
　\(\hspace{10pt}62-23=39\)
　\(\hspace{10pt}62-19=43\)
出も良いです。

【結論】部分はこの差です。
　\(\hspace{10pt}\underline{　4　}(日)\)

答え　ア　\(\,39\,\)　イ　\(\,43\,\)　ウ　\(\,4\,\)

問２
問１の結果はたまたまなのか「２０年」と「１０年」分で見ています。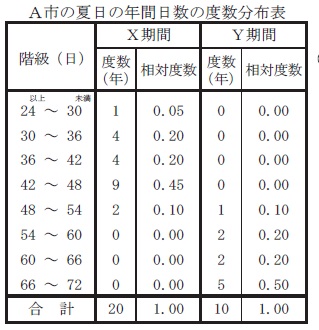
(1)
相対度数の度数折れ線を書きます。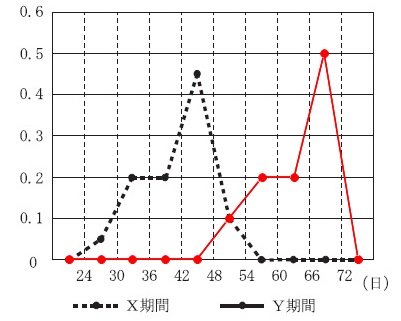各階級の中央値が階級値になるので、
点の取る位置を間違えないようにしましょう。
それと度数折れ線は、
度数分布表にある階級のもう一つ上と下に\(\,0\,\)という度数がある、
として表すので忘れないようにしましょう。