2023年(令和5年)度秋田県公立高校入試の数学の問題と解説（前半）

2023年(令和5年)度秋田県公立高校入試の数学の問題と解説のです。
大問で５問は例年通りで問題数はかわりはなく、
高校ごとに指定の問題がありますので選択を間違えるというミスは無くしましょう。
前半となるこのページは配点の半分以上となる第１問と第２問ですが、
抑えておく基本ポイントは多いですよ。

※
後半の解説は更新後に下部にリンクさせておきます。

2023年(令和5年)度秋田県公立高校入試の数学の問題

令和５年度秋田県公立高校入試の数学の問題です。

⇒　2023年(令和5年)度秋田県公立高校入試の数学の問題ＰＤＦ

選択問題は受験する高校から指定されるので指定問題は間違えないようにしましょう。
１問１問の配点は小さくないのでミスは大きいです。

2023年(令和5年)度秋田県公立高校入試の数学の解説

大問\(\,1\,\)から\(\,5\,\)まであります。
選択問題もあり問題数が多くなるのでできるだけ簡単に解説しておきます。
一気に最後まで行こうと考えていましたが、
偏りの少ない問題構成で抑えるポイントが多いので前半後半でページを変えることにしました。
どうぞご了承下さい。

第１問

\(\,\large{1}\,\)
(1)
　\(\hspace{10pt}8+\color{red}{12\div (-4)}\\
=8\color{red}{-3}\\
=\underline{　5　}\)

計算順序を間違えなければ問題ないでしょう。
掛け算割り算が先です。

(2)
　\(\hspace{10pt}12ab\color{red}{\div 6a^2}\times 2b\\
\displaystyle =\frac{12ab\times 2b}{\color{red}{6a^2}}\\
\displaystyle =\underline{\underline{　\frac{4b^2}{a}　}}\)

数字でも文字式でも割り算は分数で処理すると早いです。
（(1)は割り算部分がすぐに割り切れると分かるので暗算しています。）

ここがピンとこない人は当会の『覚え太郎』シリーズを強くお勧めします。

(3)
　\(\hspace{10pt}4=\sqrt{16}\)
なので、
　\(\hspace{10pt}\underline{　4\,＞\,\sqrt{10}　}\)

会員にはいうまでもないですが数の大小比較は、
数の世界の統一が基本です。

(4)
代入です。
　\(\hspace{10pt}\displaystyle \color{red}{x=\frac{1}{2}}\,,\,\color{blue}{y=-3}\)

与式を先に計算しておきます。
　\(\hspace{10pt}2(x-5y)+5(2x+3y)\\
=2x-10y+10x+15y\\
=12\color{red}{x}+5\color{blue}{y}\\
\displaystyle =12\times \left(\color{red}{\frac{1}{2}}\right)+5\times (\color{blue}{-3})\\
=6-15\\
=\underline{　-9　}\)

いきなり代入しても大した計算ではありませんが。
代入問題は与式（求値式）を簡単にしてから代入する方が早いことが良いです。

(5)
　\(\hspace{10pt}\displaystyle \frac{\sqrt{2}}{2}-\color{red}{\frac{1}{3\sqrt{2}}}\\
\displaystyle =\frac{\sqrt{2}}{2}-\color{red}{\frac{\sqrt{2}}{6}}\\
\displaystyle =\frac{3\sqrt{2}-\sqrt{2}}{6}\\
\displaystyle =\frac{2\sqrt{2}}{6}=\underline{\underline{　\frac{\sqrt{2}}{3}　}}\)

無理数計算は慣れによって暗算度合いが変わりますが、
分母の有理化はていねいにした方がミスは減ります。
後の分数計算は文字式でもすべて同じです。
（会員はいつも通り分母をひとつにして分子の計算に集中するように。）

(6)
　\(\begin{eqnarray}\displaystyle
\frac{5x-2}{4}&=&7\\
5x-2&=&7\times 4\\
5x&=&28+2\\
x&=&\underline{　6　}
\end{eqnarray}\)

分数のまま処理しても良いですけど、
最初に分母をなくした方が\(\,\color{red}{方程式では楽}\,\)です。

(7)
連立方程式は基本通り一文字消去しましょう。
　\( \begin{cases}
\hspace{4pt} 2x+y=5\\
\hspace{4pt} x-4y=7
\end{cases}\)

どちらでも良いですがここでは\(\,x\,\)を先に消去しておきます。
　\(\hspace{14pt}2x+\hspace{4pt}y=5\\
\underline{-\,)\,2x-8y=14}\\
\hspace{36pt}9y=-9\\
\hspace{40pt}y=\underline{　-1　}\)

第２方程式に戻して
　\(\begin{eqnarray}\displaystyle
x-4y&=&7\\
x-4(-1)&=&7\\
x&=&7-4\\
&=&\underline{　3　}
\end{eqnarray}\)

答え　\(\,\underline{　x=3\,,\,y=-1　}\,\)

出てきた答えを他の方程式に代入して成り立つか確認すれば、
計算ミスの確認ができますよ。

(8)
２次方程式です。
　\(\hspace{4pt}x^2+5x+2=0\)

因数分解できないので解の公式です。
　\(\begin{eqnarray}\displaystyle
x&=&\frac{-5\pm \sqrt{5^2-4\cdot 1\cdot 2}}{2}\\
&=&\frac{-5\pm \sqrt{25-8}}{2}\\
&=&\underline{\underline{　\frac{-5\pm \sqrt{17}}{2}　}}
\end{eqnarray}\)

解の公式は導けることより使えることが先で良いです。
⇒　２次方程式の解の公式二通りの求め方と便利な公式と文章題の解き方

過去に中学の数学から解の公式がない時期が一時期あったのですが、
やはり使えること前提の方が応用範囲がかなり広がるのですぐに帰ってきました。

(9)
長さを文字で表します。

誤答が多かったと思われる点があるので先に書いておきますが、
正三角形が３つ並べられていますが位置関係が微妙です。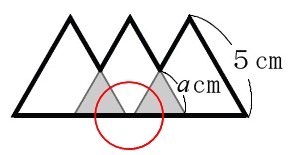問題用紙でパッと見た目には左右の正三角形が頂点でつながっているように感じたかもしれませんが、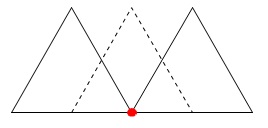長さ\(\,a\,\)によって変わるので注意です。

そこにさえ気をつければ簡単です。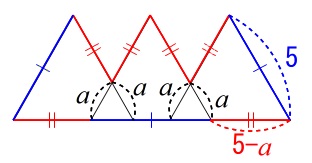長さ\(\,\color{red}{5-a}\,\)の赤い線分が６つと、
青い線分\(\,\color{blue}{5}\,\)が３つの和が周囲の長さになります。
　\(\hspace{10pt}6(\color{red}{5-a})+3\times \color{blue}{5}\\
=30-6a+15\\
=\underline{　45-6a　}\mathrm{cm}\)

底になっているところは部分的に\(\,a\,\)を使って表せるので出してみても良いです。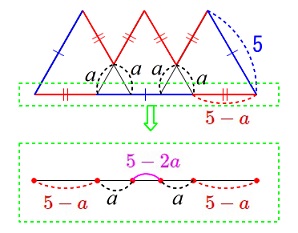底辺部分の１つの長さが\(\,\color{blue}{5}\,\)で良いことも納得できます。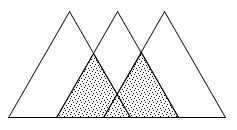重なる部分が正三角形といえないような場合でも、
文字式としては成立することは分かるでしょう。
問題としては設定がややこしくなるのですが、
この問題では条件を絞ってあるので考えなくて良いです。

(10)
素数を求めます。

忘れがちですが、\(\,1\,\)という数は素数ではありません。
⇒　素数とは？素因数分解の方法と平方根の求め方(ルートの使い方準備)　

条件は\(\,n\,\)が\(\,100\,\)より小さい素数であることと、
　\(\hspace{4pt}\displaystyle \frac{231}{n+2}\,\)が整数
になることです。

割り算を\(\,99\,\)回しても良いですが時間が足りなくなります。
素因数分解を利用しましょう。
　\(\hspace{4pt}231=3\times 7\times 11\)
（分子の\(\,231\,\)は\(\,3\,\)の倍数なので先ず\(\,3\,\)で割ると素因数分解が簡単です。）
⇒　覚えておいた方がいい倍数の見分け方

このことから分母である\(\,n+2\,\)が素因数の掛け算でできる
　\(\hspace{4pt}3\,,\,7\,,\,11\,,\,3\times 7\,,\,3\times 11\,,\,7\times 11\,,\,3\times 7\times 11\)
のどれかであれば良いことになります。
　\(\begin{eqnarray}\displaystyle \color{red}{n}+2&=&3\,,\,7\,,\,11\,,\,21\,,\,33\,,\,77\,,\,231\\
\color{red}{n}&=&1\,,\,5\,,\,9\,,\,19\,,\,31\,,\,75\,,\,229
\end{eqnarray}\)
このうち\(\,100\,\)より小さい素数は
　\(\hspace{4pt}\underline{　5\,,\,19\,,\,31　}\)

条件から\(\,229\,\)という数が素数かは考えなくて良いです。
（素数です。）

(11)
角度を求めますが四角形の内角の和が\(\,360°\,\)であることから求まります。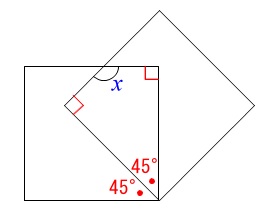計算はお任せします。
　\(\hspace{4pt}∠x=\underline{　135°　}\)

(12)
ここも角度です。
直径という条件も２つあるのでいろいろな方向があって良いと思います。

ここでは素直に中心角から円周角につなげておきます。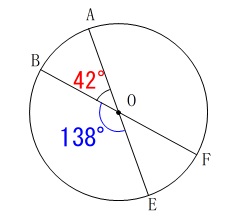条件から\(\,\mathrm{∠AOB=\color{red}{42°}}\,\)なので
反対の角が\(\,\mathrm{∠BOE=\color{blue}{138°}}\,\)となります。

点\(\,\mathrm{C\,,\,D}\,\)は\(\,\stackrel{\large{\frown}}{\mbox{BE}}\,\)を３等分するので、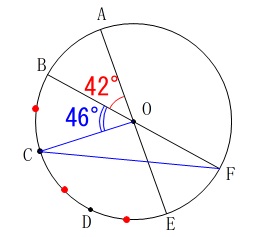中心角が\(\,\mathrm{∠BOC=46°}\,\)なので
　\(\hspace{10pt}\mathrm{∠BFC}=∠x=\underline{　23°　}\)

円周角の性質から\(\,\mathrm{∠CFE}=2\,∠x\,\)なので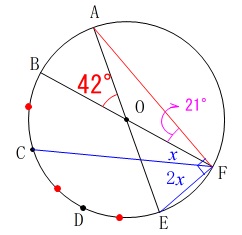\(\,x\,\)を角度を表す数値として計算すると
　\(\begin{eqnarray}
21+x+2x&=&90\\
x&=&23
\end{eqnarray}\)
でも良いです。
（問題では\(\,x\,\)は角度ではなく位置を表しているのでややこしくてすみません。）

(13)
長さを求めますが、
単なる相似比を利用するだけなので簡単に済ませます。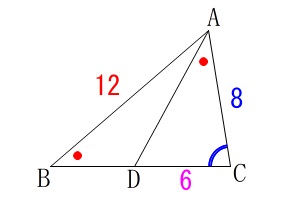２つの角がそれぞれ等しいので
　\(\,\mathrm{△ABC}\,\)　∽　\(\,\mathrm{△DAC}\,\)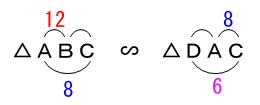相似比から
　\(\begin{eqnarray}\displaystyle
\mathrm{AB:DA}&=&\mathrm{AC:DC}\\
12:\mathrm{DA}&=&8:6\\
8\times \mathrm{DA}&=&6\times 12\\
\mathrm{DA}&=&\frac{6\times 12}{8}=\underline{　9　}\mathrm{cm}
\end{eqnarray}\)

(14)
長い条件がありますが、
容器を転がしたあとの水面の高さを求めます。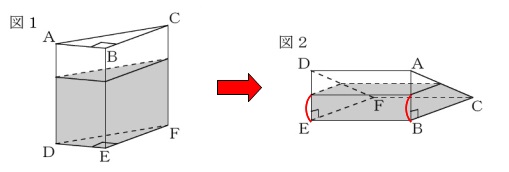水の容量からでも良いですが、
容器自体の全体体積が変わらないことからすき間の体積で進めます。

長さが与えられているので確認しておきましょう。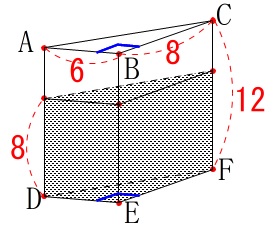すき間分で進ますが、
水の容量でも良いのでどちらも出しておきます。

水の体積\(\,V_1\,\)は
　\(\begin{eqnarray}
V_1&=&\frac{1}{2}\times 6\times 8\times 8\\
&=&192
\end{eqnarray}\)

すき間部分の体積\(\,V_2\,\)は
　\(\begin{eqnarray}\displaystyle
V_2&=&\frac{1}{2}\times 6\times 8\times 4\\
&=&\color{red}{96}
\end{eqnarray}\)

合わせて容器全体の体積になっていることを確認すると良いです。
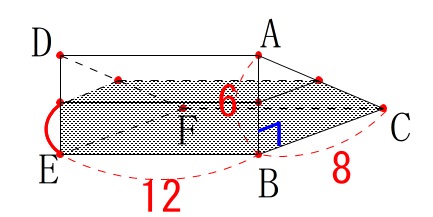水面の\(\,\mathrm{AB}\,,\,\mathrm{AC}\,\)上の点を図のように\(\,\mathrm{G\,,\,H}\,\)とします。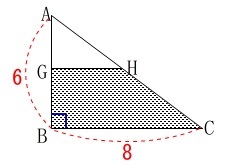\(\,\mathrm{△ABC}\,\)を抜き出してみると分かり易いです。
水面までの高さ\(\,\mathrm{GB}\,\)を文字でおいても良いですが、
計算しやすい文字設定で先に答えを出しておきます。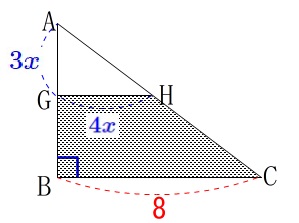\(\,\mathrm{AB:BC=3:4}\,\)なので、
\(\,\mathrm{AG}\,\)を\(\,x\,\)を正の数として\(\,\color{blue}{3x}\,\)とすると、
\(\,\mathrm{GH}=\color{blue}{4x}\,\)とおけるので隙間部分の体積\(\,V_2\,\)から
　\(\begin{eqnarray}\displaystyle
V_2&=&\frac{1}{2}\times \mathrm{AG}\times \mathrm{GH}\times 12\\
\color{red}{96}&=&\frac{1}{2}\times 3x\times 4x\times 12　･･･①\\
x^2&=&\frac{4}{3}\\
x&=&\pm \frac{2\sqrt{3}}{3}\\
x&=&\color{magenta}{\frac{2\sqrt{3}}{3}}\,(,＞\,0\,)
\end{eqnarray}\)

このことから
　\(\hspace{10pt}\displaystyle \mathrm{AG}=\color{blue}{3x}\,=\,3\times \color{magenta}{\frac{2\sqrt{3}}{3}}=2\sqrt{3}\)
よって水面までの高さは\(\,\mathrm{AB}\,\)が\(\,\color{red}{6}\,\)なので
　\(\hspace{10pt}\mathrm{GB}=\underline{　6-2\sqrt{3}　}\,\mathrm{cm}\)

少し技巧的？に計算するなら①の後
　\(\begin{eqnarray}\displaystyle
\color{red}{96}&=&\frac{1}{2}\times 3x\times 4x\times 12　･･･①\\
72x^2&=&96\\
9x^2&=&12\\
(3x)^2&=&12\\
3x&=&\pm 2\sqrt{3}
\end{eqnarray}\)
と\(\,\mathrm{AG}\,\)を出せます。

まあ、最初から\(\,\mathrm{AG}\,=\,a\,\)とおいても分数になるとはいえ、
どれほどややこしくはないですよ。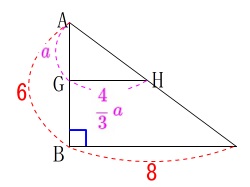　\(\,\mathrm{AG}=\color{magenta}{a}\,,\,\displaystyle \mathrm{GH}=\color{magenta}{\frac{4}{3}\,a}\,\)
とすると
　\(\begin{eqnarray}
V_2&=&\frac{1}{2}\times a\times \frac{4}{3}\,a\times 12\\
96&=&8a^2\\
a^2&=&12\\
a&=&\pm 2\sqrt{3}
\end{eqnarray}\)

こっちの方がすっきりしますね。

求めたい水面の高さ\(\,\mathrm{GB}\,\)を\(\,\color{red}{h}\,\)としても求めておきます。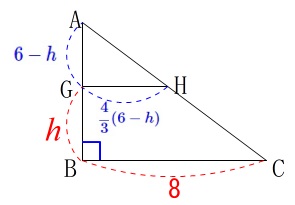　\(\hspace{4pt}\mathrm{GB}=\color{red}{h}\,\)
とすると
　\(\hspace{4pt}\mathrm{AG}=\color{blue}{6-h}\,,\,\displaystyle \mathrm{GH}=\color{blue}{\frac{4}{3}(6-h)}\)
となるので
　\(\begin{eqnarray}
V_2&=&\frac{1}{2}\times (6-h)\times \frac{4}{3}(6-h)\times 12\\
96&=&8(6-h)^2\\
(6-h)^2&=&12\\
6-h&=&\pm 2\sqrt{3}\\
h&=&6\pm 2\sqrt{3}
\end{eqnarray}\)

水面の高さは\(\,\mathrm{AB}\,\)の\(\,6\,\)より小さいので
　\(\hspace{4pt}\mathrm{GB}=h=6-2\sqrt{3}\)

どれでも計算量に大した差はないので良いですね。

水の量から求める方向も説明した方が良いかもそれませんが、
長くなったので、
　台形\(\,\mathrm{GBCH}\,\)を底面、高さを\(\,\mathrm{BE=12}\,\)
として自分でやってみて下さい。
（文字の置き方はすき間のときと同じでどれでも良いです。）
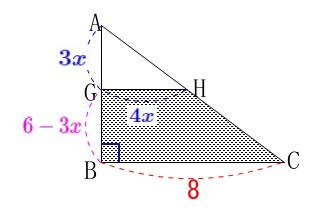　\(\begin{eqnarray}
V_1&=&\frac{\color{blue}{4x}+\color{red}{8}}{2}\times (\color{magenta}{6-3x})\times 12\\
192&=&2(x+2)\times 36(2-x)\\
9x^2&=&12
\end{eqnarray}\)

続きはお任せします。

(15)
円錐の表面積を求めます。

問題に「表面積」とあるのでやることは１つです。
『覚え太郎』で確認しておきましょう。

円錐の底面の半径が\(\,\color{red}{4}\,\)なので
底面の円周は
　\(\hspace{10pt}2\,\pi\,(4)=\color{red}{8\pi}\)
円錐が３回半だけ回転して１周したので
点線の円周は（図の青の円）
　\(\hspace{4pt}\displaystyle \frac{7}{2}\times \color{red}{8\pi}=\color{blue}{28\,\pi}\)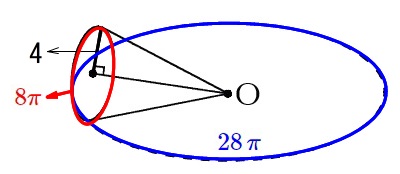このことから元の円錐の母線は、
青い円の半径と同じで\(\,\color{blue}{14}\,\)になります。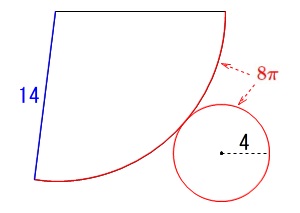　展開図は図のようになりますね。
（中心角は適当で良いですよ。）

よって求める表面積\(\,S\,\)は
　\(\begin{eqnarray}
S&=&\frac{1}{2}\times 8\,\pi\times 14+\pi\,(4)^2\\
&=&56\,\pi+16\,\pi\\
&=&\underline{　72\,\pi　}\mathrm{cm^2}
\end{eqnarray}\)
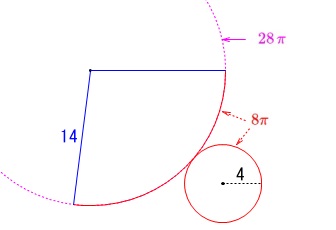　おうぎ形の部分の面積\(\,S_1\,\)は、
半径の\(\,\color{blue}{14}\,\)の円周が\(\,\color{magenta}{28\,\pi}\,\)だから弧との比から
　\(\begin{eqnarray}
S_1&=&\pi\,(14)^2\times \frac{8\,\pi}{28\,\pi}\\
&=&56\,\pi
\end{eqnarray}\)
となります。
（\(\,28\pi\,\)ってさっき見た？それは母線の\(\,14\,\)を出すために使ったものだから当然です。）

やっと\(\,1\,\)が終わりました。
（実際の試験で解答するのは\(\,15\,\)問中の\(\,8\,\)問です。）

第２問

\(\,\large{2}\,\)
１次関数と確率と作図があります。

簡単にすませますので問題はよく読んでおいて下さい。

(1)
移動して、休憩して、走ってと速さが変わりますが、
移動中は一定の速さなので直線的な動きになります。
①
グラフを書き込みます。
午前\(\,10\,\)時\(\,0\,\)分が原点になるのでそこから直線を書き込んで行けば良いです。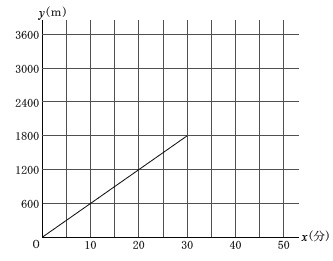午前\(\,10\,\)時に出発し毎分\(\,60\mathrm{m}\,\)の速さで\(\,1800\mathrm{m}\,\)移動するので
　\(\hspace{4pt}\displaystyle \frac{1800}{60}=30\,(分)\)
休憩時間は分かりません。（ここまでがグラフにあります。）

この先は逆にたどりましょう。
午前\(\,10\,\)時\(\,50\,\)分に図書館に着いたということなので、
残りの\(\,1800\mathrm{m}\,\)を毎分\(\,120\mathrm{m}\,\)の速さで移動するので、
走った時間は
　\(\hspace{4pt}\displaystyle \frac{1800}{120}=15\,(分)\)

つまり午前\(\,10\,\)時\(\,35\,\)分から走り出したということです。
（休憩中は移動はしないので横ばいの直線です。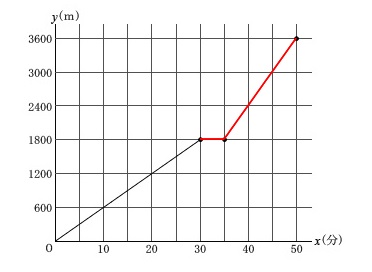）走り出した点を出しましたが、
速さが２倍（傾きが２倍）で図書館に着いた時刻から考えれば、
走っている時間は考えなくてもグラフはかけますね。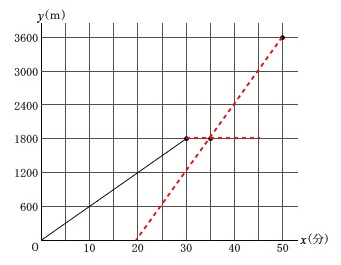この問題は５分間隔で線を入れてくれていたので、
ちょうど交点でグラフが変化していたので書きやすいです。

②
グラフの交点の\(\,x\,\)座標を求める問題です。
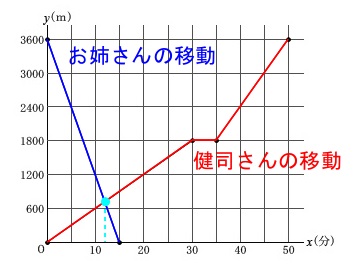お姉さんは毎分\(\,240\mathrm{m}\,\)で図書館から逆に移動してくるので、
移動を表す関数は
　\(\hspace{4pt}y=3600-240x\)
駅まで\(\,15\,\)分なので健司さんの移動を表す関数が
　\(\hspace{4pt}y=60x\)
の区間で出会うから２つの関数を連立して
　\(\begin{eqnarray}
60x&=&3600-240x\\
300x&=&3600\\
x&=&12
\end{eqnarray}\)

答え　午前\(\,\,10\,\,\)時\(\underline{　\,12\,　}分\)

「出会う」というのはグラフでいいうと『交点』です。

(2)
確率です。
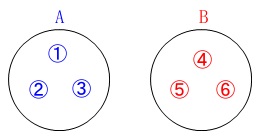袋\(\,\mathrm{A\,,\,B}\,\)の中に数字が書かれたカードが３枚ずつ入っています。
①
１枚ずつ取り出した数の積が奇数になる確率です。
樹形図で良いですがここでは表で見ておきます。
　\(\begin{array}{|c|c|c|c|} \hline
& \color{blue}{1} & \color{blue}{2} & \color{blue}{3} \\ \hline
\,\color{red}{4}\, & & & \\ \hline
\color{red}{5} & ○ & & ○ \\ \hline
\color{red}{6} & & & \\ \hline
\end{array}\)
積が奇数になるのは両方から奇数を取り出した場合だけです。
答え　\(\hspace{4pt}\displaystyle \underline{\underline{　\frac{2}{9}　}}\)

※（別解）
例えばコインが表か裏かの確率は\(\,\displaystyle \frac{1}{2}\,\)です。
じゃあ、２回続けて表が出る確率は、
と聞かれたら\(\,\displaystyle \frac{1}{2}\times \frac{1}{2}=\frac{1}{4}\)と求める事ができます。
他にもさいころの\(\,1\,\)の目が出る確率は\(\,\displaystyle \frac{1}{6}\,\)です。
では２回続けて１が出る確率は、と聞かれたら
　\(\hspace{4pt}\displaystyle \frac{1}{6}\times \frac{1}{6}=\frac{1}{36}\)
とするのは慣れていませんか？
同じように続けて起こる事象の確率は掛け算で出せます。袋\(\,\mathrm{A}\,\)から奇数を取り出す確率は\(\,\displaystyle \frac{2}{3}\,\)で、
袋\(\,\mathrm{B}\,\)から奇数を取り出す確率は\(\,\displaystyle \frac{1}{3}\,\)なので、
　\(\hspace{4pt}\displaystyle \frac{2}{3}\times \frac{1}{3}=\underline{　\frac{2}{9}　}\)
分かっている人もいるとは思いますが、
慣れていない人にも分かる説明をしておきました。
（後の問題で使ってみますので覚えておいて下さい。）

②
これも２つの袋から取り出した数字の積ですが、
偶数となる確率と奇数になる確率が等しいときです。

袋\(\,\mathrm{B}\,\)に加える数字\(\,\color{magenta}{7}\,\)のカードがあります。
\(\,6\,\)枚用意されています。

何枚加えれば条件を満たすかを求めます。
\(\,1\,\)枚から\(\,6\,\)枚まで\(\,①\,\)と同じように調べれば答えは出ます。
１枚加えるとき\(\,\mathrm{A}\,\)は３枚、\(\,\mathrm{B}\,\)は４枚となるので
　\(\begin{array}{|c|c|c|c|} \hline
& \color{blue}{1} & \color{blue}{2} & \color{blue}{3} \\ \hline
\,\color{red}{4}\, & & & \\ \hline
\color{red}{5} & ○ & & ○ \\ \hline
\color{red}{6} & & & \\ \hline
\color{magenta}{7} & ○ & & ○ \\ \hline
\end{array}\)
奇数になる確率は
　\(\hspace{4pt}\,\displaystyle \frac{4}{12}=\frac{1}{3}\,\)
で偶数になる確率の方が大きい。
（分子は\(\,\mathrm{A\,,\,B}\,\)にある奇数の枚数の積、分母は袋にある枚数の積です。）

２枚加えるとき\(\,\mathrm{A}\,\)は３枚、\(\,\mathrm{B}\,\)は５枚となるので
（袋\(\,\mathrm{A}\,\)に奇数は\(\,\color{red}{2}\,\)枚、袋\(\,\mathrm{B}\,\)には奇数が\(\,\color{blue}{3}\,\)枚）
　\(\begin{array}{|c|c|c|c|} \hline
& \color{blue}{1} & \color{blue}{2} & \color{blue}{3} \\ \hline
\,\color{red}{4}\, & & & \\ \hline
\color{red}{5} & ○ & & ○ \\ \hline
\color{red}{6} & & & \\ \hline
\color{magenta}{7} & ○ & & ○ \\ \hline
\color{magenta}{7} & ○ & & ○ \\ \hline
\end{array}\)
奇数になる確率は\(\,\displaystyle \frac{\color{red}{2}\times \color{blue}{3}}{3\times 5}=\frac{2}{5}\,\)で違います。
（樹形図と同じなのでカード\(\,\color{magenta}{7}\,\)は区別して考えますよ。）

３枚加えるとき\(\,\mathrm{A}\,\)は３枚、\(\,\mathrm{B}\,\)は６枚となるので
（袋\(\,\mathrm{A}\,\)に奇数は\(\,\color{red}{2}\,\)枚、袋\(\,\mathrm{B}\,\)には奇数が\(\,\color{blue}{4}\,\)枚）
　\(\hspace{4pt}\displaystyle \frac{\color{red}{2}\times \color{blue}{4}}{3\times 6}=\frac{4}{9}\)

続けていくと、
４枚加えるとき\(\,\mathrm{A}\,\)は３枚、\(\,\mathrm{B}\,\)は７枚となるので
（袋\(\,\mathrm{A}\,\)に奇数は\(\,\color{red}{2}\,\)枚、袋\(\,\mathrm{B}\,\)には奇数が\(\,\color{blue}{5}\,\)枚）
　\(\hspace{4pt}\displaystyle \frac{\color{red}{2}\times \color{blue}{5}}{3\times 7}=\frac{10}{21}\)
近づいてきた。

５枚加えるとき\(\,\mathrm{A}\,\)は３枚、\(\,\mathrm{B}\,\)は８枚となるので
（袋\(\,\mathrm{A}\,\)に奇数は\(\,\color{red}{2}\,\)枚、袋\(\,\mathrm{B}\,\)には奇数が\(\,\color{blue}{6}\,\)枚）
　\(\hspace{4pt}\displaystyle \frac{\color{red}{2}\times \color{blue}{6}}{3\times 8}=\frac{1}{2}\)
やっと等しくなった。

答え　\(\,\underline{　5　}\,\)枚

６枚加えるとき\(\,\mathrm{A}\,\)は３枚、\(\,\mathrm{B}\,\)は９枚となるので
（袋\(\,\mathrm{A}\,\)に奇数は\(\,\color{red}{2}\,\)枚、袋\(\,\mathrm{B}\,\)には奇数が\(\,\color{blue}{7}\,\)枚）
　\(\hspace{4pt}\displaystyle \frac{2\times 7}{3\times 9}=\frac{14}{27}\)
奇数になる確率が超えています。

この問題、たぶんこの方法を求めてはいないと思います。
ただ、６通り調べれば必ず答えは出てきますので確実ですが、
まん中当たりか上と下から順に調べて行くというのも調べる数を減らすコツです。

\(\,1\,\)から\(\,9\,\)まで調べるときは\(\,1\,,\,5\,,\,9\,\)当たりを調べてどの辺か検討をつけます。

（別解）※上の確率の積を利用します。

袋\(\,\mathrm{B}\,\)に\(\,x\,\)枚加えたとき同じ確率になるとすると
袋\(\,\mathrm{A}\,\)から奇数を取り出す確率は\(\,\displaystyle \frac{2}{3}\,\)で、
袋\(\,\mathrm{B}\,\)から奇数を取り出す確率は\(\,\displaystyle \frac{1+x}{3+x}\,\)なので、
奇数となる確率と偶数となる確率が等しいとき確率は\(\,\displaystyle \frac{1}{2}\,\)だから
　\(\begin{eqnarray}
\frac{2}{3}\times \frac{1+x}{3+x}&=&\frac{1}{2}\\
4(1+x)&=&3(3+x)\\
x&=&\underline{　5　}枚
\end{eqnarray}\)

知ってしまえば簡単なんですけどね。
袋\(\,\mathrm{B}\,\)の中にあるカードの枚数と奇数のカードの枚数を間違えないよう。

(3)
作図です。
点\(\,\mathrm{A}\,\)は接点なので垂線を引けば良いですね。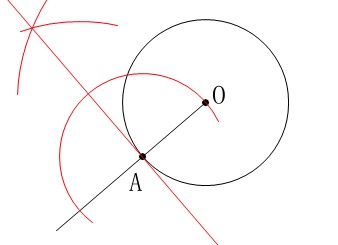点\(\,\mathrm{A}\,\)を通り直線\(\,\mathrm{AO}\,\)の垂線を引けば終わりです。

会員は作図問題集『さくっと！』の基本部分なので問題ないでしょう。

前半は以上です。

後半（第３問第４問第５問）

第３問以降は後半になります。

⇒　2023年(令和5年)度秋田県公立高校入試の数学の問題と解説（後半）

選択問題もあるので問題数が多いのでページを分けさせて頂きます。

⇒　秋田県の公立高校入試数学の過去問と解説

過去問を数年分見ればわかりますが、
例年出題分野に偏りはないので苦手分野を作らず基本を抑えておきましょう。