2023年(令和5年)度東京都公立高校入試問題【前期】数学の問題と解説

２０２３年(令和５年)度東京都公立高校入試問題【前期】数学の問題と解説です。
都立入試の数学はマークシートもあります。
他県の人にとっては少し変わっているようにも思うかもしれませんが、
この年度も非常にバランスの良い構成なので演習として過去問を利用するといいです。
※
数式の読み込みに時間がかかり遅く感じたら少し待つか、
再読み込みしてみて下さい。
よろしくお願い致します。

2023年(令和5年)度東京都公立高校入試問題【前期】数学の問題

令和５年度の都立入試前期の数学問題です。

⇒　2023年(令和5年)度東京都公立高校入試問題【前期】数学の問題ＰＤＦ

表紙からすべて東京都公表分です。
都立受験予定の人は問題だけでなく「注意書き」から読んでおきましょう。
多少の変化があったとしても対応し易くなりますよ。

2023年(令和5年)度東京都公立高校入試問題【前期】数学の解説

第１問から一気に解説します。
都立入試の数学は本当なら１問１問分けて、ていねいに解説したい問題ですよ。

長くなりそうなので早速行きます。

第１問

\(\color{black}{\fbox{1}}\)
小問集合です。

〔問１〕正の数負の数の計算です。
　\(\hspace{10pt}-8+\color{red}{6^2\div 9}\\
=-8+\color{red}{4}\\
=\underline{　-4　}\)

掛け算割り算が先ですね。

〔問２〕分数計算です。
　\(\hspace{10pt}\displaystyle \frac{7a+b}{5}-\frac{4a-b}{3}\\
\displaystyle =\frac{3(7a+b)-5(4a-b)}{15}\\
\displaystyle =\frac{21a+3b-20a+5b}{15}\\
\displaystyle =\underline{\underline{　\frac{\,a+8b\,}{15}　}}\)

慣れた計算方法で良いですが、
会員はいつも通り通分して分子の計算に集中ですよ。

〔問３〕無理数の計算です。
　\(\hspace{10pt}(\sqrt{6}-1)(2\sqrt{6}+9)\\
=12+9\sqrt{6}-2\sqrt{6}-9\\
=\underline{　3+7\sqrt{6}　}\)

過度な暗算は避けて確実に計算しましょう。

〔問４〕１次方程式です。
　\(\begin{eqnarray}
4(x+8)&=&7x+5\\
4x+32&=&7x+5\\
-3x&=&-27\\
x&=&\underline{　9　}
\end{eqnarray}\)

移項するときの符号注意です。

〔問５〕連立方程式なので一文字消去ですがどちらでも良いです。
　\( \begin{cases}
\hspace{4pt} 2x+3y=1\\
\hspace{4pt} 8x+9y=7
\end{cases}\)

代入法でもできますがここは加減法ですね。

⇒　加減法とは？連立方程式の解き方とポイント

ここでは\(\,x\,\)から消しておきます。
ご自身で確認するときは\(\,y\,\)を消去する方からどうぞ。
　\(\hspace{20pt}8x+12y=4\\
\underline{　-)\,8x+\hspace{4pt}9y=7　}\\
\hspace{50pt}3y=-3\\
\hspace{54pt}y=-1\)

第１方程式に戻して
　\(\begin{eqnarray}
2x-3&=&1\\
2x&=&4\\
x&=&2
\end{eqnarray}\)

答え　\(\,\underline{　x=2\,,\,y=-1　}\,\)

〔問６〕２次方程式です。
　\(\hspace{4pt}2x^2-3x-6=0\)

因数分解できないので解の公式を利用します。
　\(\begin{eqnarray}
x&=&\frac{3\pm \sqrt{3^2-4\cdot 2\cdot (-6)}}{2\times 2}\\
&=&\frac{3\pm \sqrt{9+48}}{4}\\
&=&\underline{\underline{　\frac{3\pm \sqrt{57}}{4}　}}
\end{eqnarray}\)

※ルートの中の「\(\,\cdot\,\)」は掛け算を意味しています。

解の公式は導けた方が良いですが、

⇒　２次方程式の解の公式二通りの求め方と便利な公式と文章題の解き方

使えることが先で良いです。（公式ですから）

〔問７〕同時に２個取り出すのと、１個ずつ取り出すのは同じです。
（同時に取り出す場合は１個目は元に戻さない取り出し方になります。）

普通に樹形図で良いですがここでは表にしておきます。
ただし青玉は４個あるので区別して
青玉を\(\,\color{blue}{1}\,,\,\color{blue}{2}\,,\,\color{blue}{3}\,,\,\color{blue}{4}\,\)としておきます。

取り出した順番は縦、横どちらでも同じです。
　\(\begin{array}{|c|c|c|c|c|c|c|} \hline
& 赤 & 白 &\,\color{blue}{1}\, & \,\color{blue}{2}\, & \,\color{blue}{3}\, &\,\color{blue}{4}\, \\ \hline
赤 & × & & & & &\\ \hline
白 & & × & & & &\\ \hline
\,\color{blue}{1}\, & & & × & ● & ● &●\\ \hline
\,\color{blue}{2}\, & & & ● & × & ● &●\\ \hline
\,\color{blue}{3}\,& & & ● & ● & × &●\\ \hline
\,\color{blue}{4}\, & & & ● & ● & ● &×\\ \hline
\end{array}\)
同時に取り出すので×の組み合わせはありません。（１個ずつでも同じ）

２個とも青になるのは\(\,●\,\)の組合わせなので
　\(\hspace{10pt}\displaystyle \frac{12}{30}=\underline{\underline{　\frac{2}{5}　}}\)
　

確率を順番に掛け算で計算できるようになると、
一つ目青玉である確率は６個中４個が青玉なので　\(\,\displaystyle \frac{4}{6}\,\)
１個減っていることに注意して、
二つ目青玉である確率は５個中３個が青玉なので　\(\,\displaystyle \frac{3}{5}\)
求める確率はこの掛け算で
　\(\displaystyle \frac{4}{6}\times \frac{3}{5}=\underline{\underline{　\frac{2}{5}　}}\)
とすることもできます。

〔問８〕角度を求めます。

直径に対する円周角が９０°であることから、
円周角の定理を利用して分かる角度を図に書き込んで行きましょう。
　\(\hspace{4pt}\mathrm{∠BAC}=\color{magenta}{20^{\circ}}\,,\,\mathrm{∠CBD}=\color{blue}{30^{\circ}}\)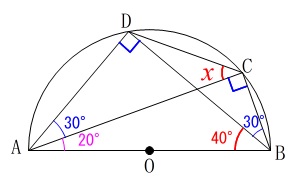直角三角形の内角と円周角の定理から、
（\(\,\mathrm{△ABD}\,\)と\(\,\mathrm{△ABC}\,\)のどちらから出も良いです。）
　\(\hspace{10pt}\mathrm{\color{red}{∠ACD}=\color{red}{∠ABD}}=\underline{　\color{red}{40^{\circ}}　}\)

答え　\(\,\underline{　40　}度\,\)

〔問９〕作図です。

点と直線の距離とは、
点から直線におろした垂線の長さです。

数学では「距離」は最短距離を意味しますので、
一番短くなる垂線のことになるのです。その距離が最も長くなるのは円の中心を通るときですね。

作図は簡単で中心\(\,\mathrm{O}\,\)から直線\(\,\ell\,\)に垂線を引けば終わりです。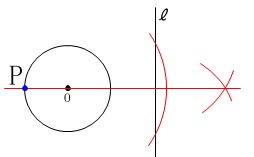会員は会員サイトにあるオリジナル作図問題集『さくっと！』は必ず繰り返し見ておきましょう。
少し難しめに構成してありますが説明を深掘りしています。
クリアーしておけば作図問題で簡単にさくっと６点ゲットできます。
（この問題は簡単なので問題集に入る前のコツやポイント解説で終わりますけどね。）

第２問

\(\color{black}{\fbox{2}}\)
文章が長いですが点の位置を読み取れれば難しくはありません。

〔問１〕

［先生が示した問題］の読み取り。
　\(\hspace{4pt}\mathrm{EF=EG=EH=EI}\)
　\(\hspace{10pt}\mathrm{AB}=a\,,\,\mathrm{FG}=b\)
および点\(\,\mathrm{P\,,\,Q\,,\,R\,,\,S}\,\)はそれぞれ図で示す線分の中点。
（この点は問題で読み取って下さい。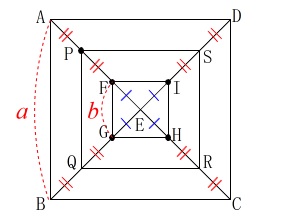）元の四角形\(\,\mathrm{ABCD}\,\)が正方形なので、
四角形\(\,\mathrm{FGHI\,,\,PQRS}\,\)ともに正方形です。

線分\(\,\mathrm{PQ}\,\)の長さは線分\(\,\mathrm{AB}\,\)と線分\(\,\mathrm{FG}\,\)の中間の長さになるので、
　\(\hspace{10pt}\displaystyle \mathrm{PQ}=\frac{a+b}{2}\)
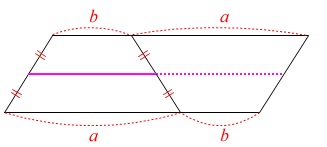台形を逆さまにして合わせると平行四辺形ができるので、
１辺の半分だという事は簡単に分かるでしょう。
これは中点でもいえるので覚えておくと良いですよ。
　中点は足して２で割る。

よって四角形\(\,\mathrm{PQRS}\,\)の周の長さ\(\,\ell\,\)は辺４つ分なので
　\(\begin{eqnarray}
\ell&=&4\times \frac{a+b}{2}\\
&=&\underline{　2a+2b　}(\,\mathrm{cm}\,)
\end{eqnarray}\)

答え　\(\,\underline{　ア　}\,\)

〔問２〕

［\(\,\mathrm{S}\,\)さんのグループが作った問題］の読み取り。

中心\(\,\mathrm{O}\,\)の四分円があって、半径がそれぞれ
　\(\hspace{10pt}\mathrm{OB}=b\,,\,\mathrm{OA}=a\)
点\(\,\mathrm{M}\,\)は線分\(\,\mathrm{AB}\,\)の中点なので、
　\(\hspace{10pt}\displaystyle \mathrm{OM}=\color{blue}{\frac{a+b}{2}}\)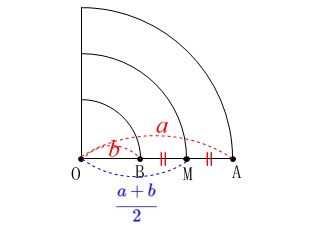線分が重なっているのでわかりにくいかもしれませんが、
中点については〔問１〕と同じです。

線分\(\,\mathrm{OA}\,\)と\(\,\mathrm{OB}\,\)を平行移動してずらすと同じだと気がつくでしょう。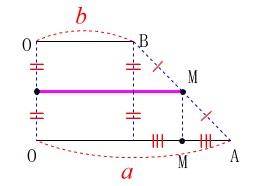ひっくり返してつなげてみて下さい。
台形のときと同じように長方形（平行四辺形）ができます。

このとき線分\(\,\mathrm{OM}\,\)を半径とするおうぎ形の弧の長さ\(\,\ell\,\)は
　\(\begin{eqnarray}\ell\,&=&\frac{1}{4}\times 2\,\pi\times \left(\color{blue}{\frac{a+b}{2}}\right)\\
&=&\color{red}{\frac{\pi}{4}(a+b)}
\end{eqnarray}\)

また線分\(\,\mathrm{OB}\,\)を半径とするおうぎ形を取り除いた部分の面積\(\,S\,\)は、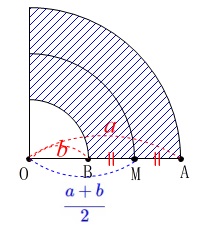半径\(\,a\,\)の円から半径\(\,b\,\)の円を取り除いて４等分した面積なので、
面積\(\,S\,\)と弧の長さ\(\,\ell\,\)との関係は
　\(\begin{eqnarray}
S&=&\frac{1}{4}\times (\pi\,a^2-\pi\,b^2\,)\\
&=&\frac{\pi}{4}(\,a^2-b^2\,)\\
&=&\color{red}{\frac{\pi}{4}(\,a+b\,)}(\,a-b\,)\\
&=&\ell\,(\,a-b\,)\\
&=&(\,a-b\,)\,\ell
\end{eqnarray}\)
（証明終わり。）

こういった関係を示す場合は、
それぞれを文字で表すことを考えていけば自ずと出ます。

第３問

\(\color{black}{\fbox{3}}\)
関数の基本と少し図形の性質との融合があります。

全体に通じる条件をまとめておきます。
　点\(\,\mathrm{A\,(\,3\,,\,-2\,)}\,\)
　直線\(\,\ell\,\)：\(\,\displaystyle y=\frac{1}{2}\,x+1\)
　点\(\,\mathrm{B：\,(-2\,,\,0\,)}\,\)
※
点\(\,\mathrm{B}\,\)は直線\(\,\ell\,\)と\(\,x\,\)軸\(\,(\,y=0\,)\,\)との交点です。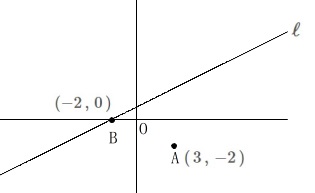点\(\,\mathrm{A\,,\,B}\,\)が固定されている事が分かればそれでいいです。

〔問１〕
点\(\,\mathrm{P}\,\)の\(\,y\,\)座標が\(\,\color{red}{-1}\,\)のときの\(\,x\,\)座標を求めます。

点\(\,\mathrm{P}\,\)は直線\(\,\mathrm{\ell}\,\)上の点なので、
　\(\displaystyle y=\frac{1}{2}\,x+1\,\)
に代入しましょう。
　\(\begin{eqnarray}
\color{red}{-1}&=&\frac{1}{2}\,x+1\\
-2&=&x+2\\
x&=&\underline{　-4　}
\end{eqnarray}\)

答え　\(\,\underline{　エ　}\,\)

〔問２〕位置関係を確認しましょう。

線分\(\,\mathrm{BP}\,\)が\(\,y\,\)軸で２等分されるとき、
点\(\,\mathrm{P}\,\)は\(\,x\,\)座標が正になります。

直線\(\,\ell\,\)の\(\,y\,\)切片が\(\,1\,\)なので、
\(\,\mathrm{P}\,\)の座標は\(\,(\,2\,,\,2\,)\,\)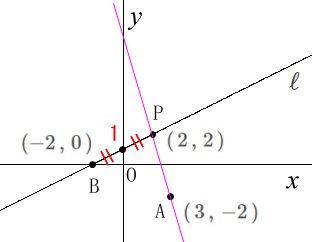よって、
求める直線\(\,m\,\)は２点
　\(\hspace{4pt}(\,2\,,\,2\,)\,,\,(\,3\,,\,-2\,)\)
を通るので、
　\(\hspace{10pt}\displaystyle \underline{　y=-4\,x+10　}\)

答え　\(\,\underline{　①　イ　②　エ　}\,\)

直線の求め方は連立方程式でも良いですが、
変化の割合から求めた方が早いです。

⇒　変化の割合とは？1次関数の求め方と直線の方程式との違い

直線は自由自在と言えるほど求められるようになっておかないと、
関数の攻略は難しいです。

〔問３〕面積が等しくなるときの点\(\,\mathrm{P}\,\)の座標を求めます。

問題は「\(\,\mathrm{△BPQ}\,\)の面積が\(\,\mathrm{△APB}\,\)の２倍」とありますが、
\(\,y\,\)軸対称があるので等しい面積と同じです。
そのことを見てから進めましょう。

直線\(\,\ell\,\)上の点\(\,\mathrm{P}\,\)と\(\,y\,\)軸対称な点\(\,\mathrm{Q}\,\)でできる\(\,\mathrm{△BPQ}\,\)が、
\(\,\mathrm{△APB}\,\)の２倍になるときです。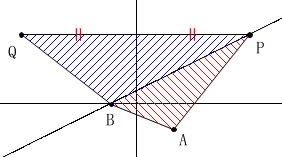ここで\(\,\mathrm{PQ}\,\)と\(\,y\,\)軸との交点を\(\,\mathrm{R}\,\)とすると、
\(\,\mathrm{△BPR}\,\)と\(\,\mathrm{△BQR}\,\)は底辺、高さとも同じなので面積が等しくなるので、
\(\,\mathrm{△APB}\,\)と\(\,\mathrm{△APR}\,\)が等しくなればいいわけです。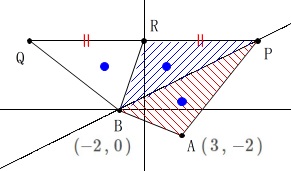点\(\,\mathrm{P}\,\)は定まっていないので座標設定して機械的に処理することもできますが、
ここでは等積移動を利用しましょう。

直線\(\,\ell\,\)と傾きが同じで点\(\,\mathrm{A}\,\)を通る直線\(\,n\,\)は
　\(\hspace{4pt}\displaystyle n\,:\,y=\frac{1}{2}\,x-\frac{7}{2}\)
なのでこの直線上の点なら\(\,\mathrm{△APB}\,\)の面積と同じ面積が得られます。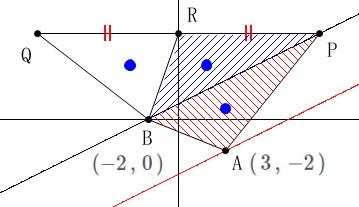ここで\(\,\mathrm{PQ}\,\)は\(\,x\,\)軸に平行で、
線分\(\,\mathrm{BP}\,\)が共通の底辺とみると\(\,x\,\)軸と直線\(\,n\,\)の交点\(\,\mathrm{A’}\,\)で、
平行四辺形\(\,\mathrm{BA’PR}\,\)とならなければなりません。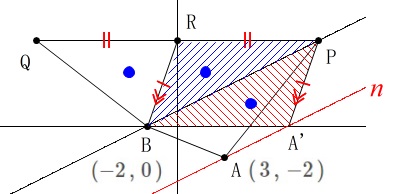直線\(\,n\,\)と\(\,x\,\)軸（\(\,y=0\,\)）との交点は、
　\(\begin{eqnarray}
0&=&\frac{1}{2}\,x-\frac{7}{2}\\
x-7&=&0\\
x&=&7
\end{eqnarray}\)

これは\(\,\mathrm{A’}\,\)の\(\,x\,\)座標です。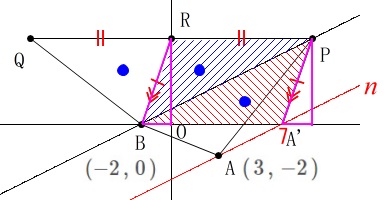平行四辺形の性質から点\(\,\mathrm{P}\,\)の座標は、
点\(\,\mathrm{B}\,\)から点\(\,\mathrm{R}\,\)に\(\,x\,\)座標は\(\,+2\,\)移動するので、
点\(\,\mathrm{P}\,\)の\(\,x\,\)座標は\(\,\color{red}{7}\,\)から\(\,+2\,\)移動して
　\(\hspace{4pt}\underline{　x=9　}\)

点\(\,\mathrm{P}\,\)を直線\(\,\ell\,\)上の点として座標設定した人もいると思います。
　\(\hspace{4pt}\displaystyle \mathrm{P}:\left(\,t\,,\,\frac{1}{2}\,t+1\,\right)\)

これが先にあれば平行四辺形の条件から\(\,\mathrm{A’}\,\)が軸上になければならないので、
　\(\,\mathrm{A’：(\,t-2\,,\,0\,)}\,\)
これが直線\(\,n\,\)上にあるはずだから
　\(\begin{eqnarray}
0&=&\frac{1}{2}\,(t-2)-\frac{7}{2}\\
t-2-7&=&0\\
t&=&\underline{　9　}
\end{eqnarray}\)

または機械的に面積計算に持って行った人もいるかもしれません。
（たぶん、会員以外はしていないと思うので計算を飛ばします。）
　\(\hspace{4pt}\begin{eqnarray}
\mathrm{△BPQ}&=&2\times \mathrm{△APB}\\
\frac{1}{2}\times 2t\times \left(\frac{1}{2}\,t+1\,\right)&=&2\times \frac{1}{2}\times \left|-2(t+2)-5\left(\frac{1}{2}\,t+1\right)\right|\\
t^2+2\,t&=&|-9t-18|
\end{eqnarray}\)
点\(\,\mathrm{P}\,\)の\(\,x\,\)座標は明らかに\(\,\mathrm{A}\,\)の\(\,x\,\)座標\(\,3\,\)より大きいので
　\(\begin{eqnarray}
t^2+2t&=&9t+18\\
t^2-7t-18&=&0\\
(t+2)(t-9)&=&0\\
t&=&-2\,,\,9
\end{eqnarray}\)
よって、
　\(\hspace{10pt}\underline{　x=9　}\)

となりますが見なくて良いです。
（見ちゃっただろうから理解できなくて気にしなくて良いです。）
ここまで『超え太郎』を使いこなせているなら等積移動の方法で終わっているはず。

第４問

\(\color{black}{\fbox{4}}\)
平面図形の問題です。

全体通しての条件を見ておきます。
これは〔問１〕〔問２〕ともに通じる条件になるので忘れないようにしましょう。

〔条件〕
四角形\(\,\mathrm{ABCD}\,\)において、
　\(\hspace{4pt}\mathrm{AD}\,\)∥\(\,\mathrm{BC}\,\)
　\(\hspace{4pt}\mathrm{AB=DC}\)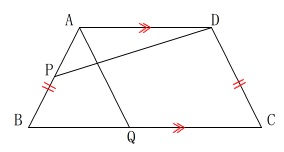四角形\(\,\mathrm{ABCD}\,\)は等脚台形です。
点\(\,\mathrm{P\,,\,Q}\,\)は固定されていません。

〔問１〕
角度を文字で表します。
〔条件〕に加えて
　\(\hspace{4pt}\mathrm{AQ}\,\)∥\(\,\mathrm{DC}\,\)
　\(\hspace{4pt}\mathrm{∠AQC}=110^{\circ}\)
　\(\hspace{4pt}\mathrm{∠APD}=a^{\circ}\)
のとき、\(\,\mathrm{∠ADP}\,\)の大きさを求めます。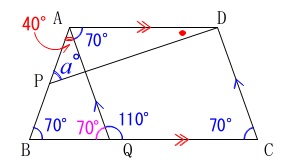四角形\(\,\mathrm{AQCD}\,\)が平行四辺形で、
\(\,\mathrm{△ABQ}\,\)が二等辺三角形なので分かる角度を書き込んでおきました。

単純に三角形\(\,\mathrm{APD}\,\)の内角の和から
　\(\begin{eqnarray}
\mathrm{∠APD+∠PAD+∠ADP}&=&180°\\
a^{\circ}+110^{\circ}+\mathrm{∠ADP}&=&180^{\circ}\\
\mathrm{∠ADP}&=&\underline{　70^{\circ}-a^{\circ}　}\\
&=&(\,70-a\,)度
\end{eqnarray}\)

答え　\(\,\underline{　ウ　}\,\)

〔問２〕
証明と面積比です。

〔条件〕に\(\,\mathrm{AC}\,\)∥\(\,\mathrm{PQ}\,\)が加わります。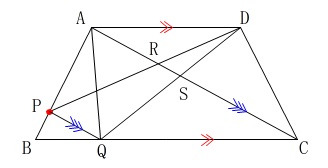
①
相似の証明です。
　\(\,\mathrm{△ASD}\,\)　∽　\(\,\mathrm{△CSQ}\,\)

⇒　中学の図形証明問題(合同･相似)の解き方と証明の書き方ポイント

平行線の錯角と対頂角から明らかなので証明は省略します。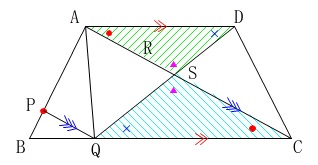平行線の錯角が等しいことだけでも良いですよ。

②
条件が加わります。
　\(\,\mathrm{AP:PB=3:1\,,\,AD:QC=2:3}\,\)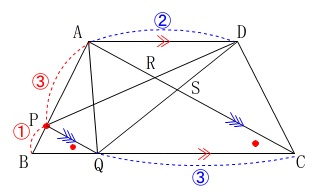\(\,\mathrm{AC}\,\)∥\(\,\mathrm{PQ}\,\)なので、
　\(\,\mathrm{△BPQ}\,\)　∽　\(\,\mathrm{△BAC}\,\)
ここで
　\(\hspace{4pt}\mathrm{BP:PA}=\color{red}{①}:\color{red}{③}\)
なので
　\(\hspace{4pt}\mathrm{BQ:QC}=\color{blue}{①}:\color{blue}{③}\)
また、\(\,\mathrm{AD:QC=\color{blue}{②}:\color{blue}{③}}\,\)だから
\(\,\mathrm{QC}\,\)の比が一致していることにも注目です。
（同じ色で表しています。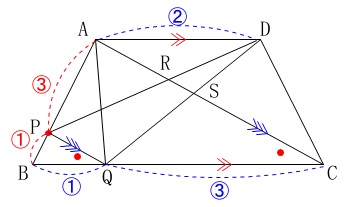）さらに\(\,\mathrm{△ASD}\,\)∽\(\,\mathrm{△CSQ}\,\)であることから
　\(\hspace{4pt}\mathrm{DS:QS}=\color{magenta}{②}:\color{magenta}{③}\)
　\(\hspace{4pt}\mathrm{AS:CS}=\color{green}{②}:\color{green}{③}\)
これから
　\(\hspace{4pt}\mathrm{PQ:RS}=⑤:②\)
これらを図示すると少しは見えてくるでしょう。
（分かることを図示することが攻略のコツです。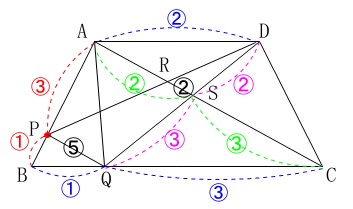）問題は\(\,\mathrm{△DRS}\,\)の面積が台形\(\,\mathrm{ABCD}\,\)の何倍か、です。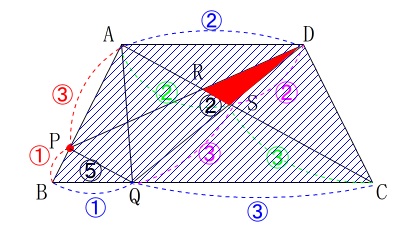比で計算を進めても良いですが、
長さが与えられていないので勝手に長さを１つ決めて進めます。

基準にするだけなので「１」でも良いですが、
（分数をできるだけ避けていきたいので）
比の与えられ方から適当な公倍数を選び\(\,\mathrm{AC=\color{red}{20}}\,\)とします。
（この数値は\(\,40\,\)でも何でも良いです。）
このとき線分比から
　\(\hspace{4pt}\mathrm{AS}=\color{red}{8}\,,\,\mathrm{CS}=\color{red}{12}\)
\(\,\mathrm{AC:PQ=4:1}\,\)になるので\(\,\mathrm{PQ=\color{red}{5}}\,\)となり、
また\(\,\mathrm{PQ:RS=⑤:②}\,\)なので
　\(\hspace{4pt}\mathrm{PQ}=\color{red}{5}\,,\,\mathrm{RS}=\color{red}{2}\)これで線分\(\,\mathrm{AC}\,\)の中で比が出ます。
　\(\hspace{4pt}\mathrm{AR:RS:CS}=\color{red}{6}:\color{red}{2}:\color{red}{12}\)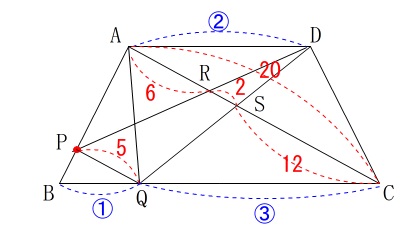ここまでくれば後は台形からの面積比を計算するのみです。

今度は台形\(\,\mathrm{ABCD}\,\)の面積を\(\,\color{blue}{S}\,\)にします。

\(\,\mathrm{AD}\,\)∥\(\,\mathrm{BC}\,\)の台形なので高さは同じとみて、
　\(\begin{eqnarray}\mathrm{△ADC:△ABC}&=&\mathrm{AD:BC}\\
&=&\color{blue}{②}:(\,\color{blue}{①}+\color{blue}{③}\,)\\
&=&1:2
\end{eqnarray}\)
だから\(\,\mathrm{△ADC}\,\)の面積は台形\(\,\mathrm{ABCD}\,\)の\(\,\displaystyle \frac{1}{3}\,\)となるので
　\(\hspace{4pt}\displaystyle \mathrm{△ADC}=\frac{1}{3}\times \color{blue}{S}\)

また、\(\,\mathrm{△DRS}\,\)の面積は底辺\(\,\mathrm{AC}\,\)の比から\(\,\mathrm{△ADC}\,\)と比べると
　\(\begin{eqnarray}
\mathrm{△DRS}&=&\frac{\color{red}{2}}{\color{red}{6}+\color{red}{2}+\color{red}{12}}\times \mathrm{△ADC}\\
&=&\frac{1}{10}\times \mathrm{△ADC}
\end{eqnarray}\)

よって、
　\(\begin{eqnarray}
\mathrm{△DRS}&=&\frac{1}{10}\times \frac{1}{3}\times \color{blue}{S}\\
&=&\underline{\underline{　\frac{1}{30}　}}\times S
\end{eqnarray}\)

答え　\(\displaystyle \underline{\underline{　\frac{1}{30}\,（倍）}}\)

線分\(\,\mathrm{AC}\,\)を分ける比が必要だと気がつけば、
自ずと相似比利用の方針は決まってくるでしょう。

第５問

正四面体の動点問題です。

〔条件〕
正四面体の１辺は\(\,6\,\mathrm{cm}\,\)。
各点は図の通りで\(\,\mathrm{M}\,\)は\(\,\mathrm{AC}\,\)の中点。
点\(\,\mathrm{P}\,\)は毎秒\(\,\mathrm{1\,cm}\,\)で\(\,\mathrm{A\rightarrow B\rightarrow C}\,\)と動く。
点\(\,\mathrm{Q}\,\)は毎秒\(\,\mathrm{1\,cm}\,\)で\(\,\mathrm{C\rightarrow D\rightarrow A}\,\)と動く。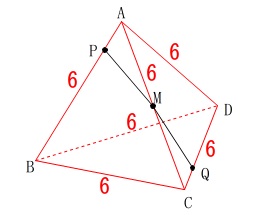正四面体の各面は正三角形です。

〔問１〕線分と線分の和が最も小さくなるときですが、
言うまでもありませんね。
　\(\hspace{4pt}\mathrm{MP+MQ}=\ell\)

\(\,\ell\,\)の値が最も小さくなるのは何秒後か、が問題です。

会員の方は迷わなかったでしょう。
\(\,\mathrm{△ABC}\,\)と\(\,\mathrm{△ACD}\,\)の部分の展開図を書くとひし形になります。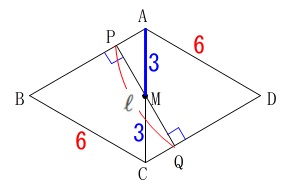線分の和\(\,\ell\,\)が最も短くなるのは、
\(\,\mathrm{M}\,\)から\(\,\mathrm{AB\,,\,DC}\,\)に引いた垂線の和になります。
※
２つの点は同じ速さで移動するので\(\,\mathrm{PMQ}\,\)は直線になりますが、
最小になるのは平行四辺形の高さとなるとき（垂線）です。

このとき\(\,\mathrm{△MAP}\,\)は三角定規になるので
　\(\begin{eqnarray}
\mathrm{AP:AM}&=&1:2\\
\mathrm{AP}:\color{blue}{3}&=&1:2\\
\mathrm{AP}&=&\frac{3}{2}
\end{eqnarray}\)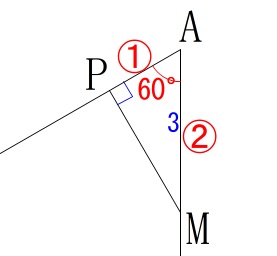速さは\(\,1\,\)なので線分\(\,\mathrm{AP}\,\)の長さは時間と同じになります。
（線分\(\,\mathrm{AB}\,\)上にいる間は、です。）

答え　\(\displaystyle \underline{\underline{　\frac{3}{2}　}}\,(\,秒後\,)\)

〔問２〕体積を求めます。

点\(\,\mathrm{P}\,\)が\(\,\mathrm{A}\,\)を出発してから８秒後のときの、
立体（三角すい）\(\,\mathrm{Q-APM}\,\)の体積です。点\(\,\mathrm{P}\,\)が出発してから\(\,8\,\)秒後に固定されるので、
各点の位置を確認しておきましょう。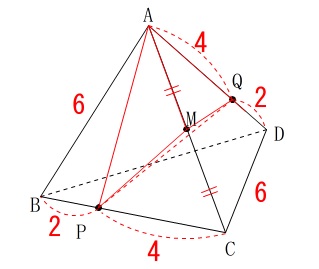ちょっとずるいですが、
答えを先に出させて頂きます。
　\(\begin{eqnarray}
V&=&\frac{\sqrt{2}}{12}\times 6^3\times \frac{1}{2}\times \frac{4}{6}\times \frac{4}{6}\\
&=&4\sqrt{2}
\end{eqnarray}\)

正四面体の体積から底面の縮小、高さの縮小で求めておきました。
（単なる計算ミス確認用です。）

正四面体の体積の公式は覚えておくようにはお勧めしていません。
というのも公式を覚えて使うよりも、
高さを求める（公式を導く）事を問われる内容の問が多いので覚えても良いですが、
四面体の体積においては「求め方」を覚えておくことをお勧めしています。
（高さの求め方も後で説明します。）

もちろん覚えている人は使って良いです。（公式ですから。）

求める立体は三角すいです。
底面を\(\,\mathrm{△APM}\,\)とするか\(\,\mathrm{△AQM}\,\)とするか分かれますが、
頂点が\(\,\mathrm{AD}\,\)上にある方を選んだ方が良いです。

問題が示している通り\(\,\mathrm{△APM}\,\)を底面とする方ですね。
理由は高さとなる垂線が中線上に下りるからです。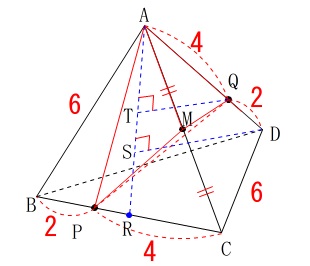\(\,\mathrm{△AQM}\,\)を底面とするなら頂点が\(\,\mathrm{AB}\,\)上にある場合です。

それでは底面となる\(\,\mathrm{△APM}\,\)の面積\(\,S\,\)、
高さとなる\(\,\mathrm{QT}\,\)の長さ\(\,h\,\)を求めて、
三角すいの体積\(\,V\,\)を求めましょう。

底面積となる\(\,\mathrm{△APM}\,\)の面積\(\,S\,\)は、
線分\(\,\mathrm{BM}\,\)が正三角形の中線なので分かり易いです。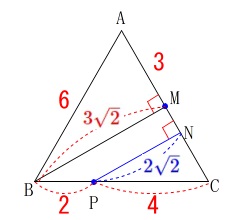\(\,\mathrm{△ABM}\,\)は三角定規と同じ比だから
　\(\hspace{4pt}\mathrm{BM}=\color{red}{3\sqrt{2}}\)
点\(\,\mathrm{P}\,\)から\(\,\mathrm{AC}\,\)に下ろした垂線の長さは\(\,\mathrm{BP\,,\,PC}\,\)の比から
　\(\begin{eqnarray}
\mathrm{BM:PN}&=&(\color{red}{2}+\color{red}{4}):\color{red}{4}\\
3\sqrt{3}:\mathrm{PN}&=&3:2\\
\mathrm{PN}&=&\color{blue}{2\sqrt{2}}
\end{eqnarray}\)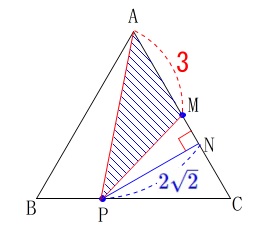このことから底面積となる\(\,\mathrm{△APM}\,\)の面積\(\,S\,\)は
　\(\begin{eqnarray}
S&=&\frac{1}{2}\times \mathrm{AM}\times \mathrm{PN}\\
&=&\frac{1}{2}\times 3\times 2\sqrt{3}\\
&=&\color{magenta}{3\sqrt{3}}
\end{eqnarray}\)

次は三角すいの高さとなる\(\,h\,\)です。

先に書いておいた通りで、
線分\(\,\mathrm{AD}\,\)上の点から面\(\,\mathrm{ABC}\,\)に垂線を下ろすと、
\(\,\mathrm{△ABC}\,\)の\(\,\mathrm{A}\,\)から\(\,\mathrm{BC}\,\)に引いた中線上に下ります。
（説明がくどくなりますが大切なポイントなので確認しておいて下さい。）ここで求める三角すいの高さは線分\(\,\mathrm{QT}\,(\,h\,)\,\)になります。

頂点\(\,\mathrm{D}\,\)から\(\,\mathrm{△ABC}\,\)に下ろした垂線は\(\,\mathrm{△ABC}\,\)の重心で交わるので、
点\(\,\mathrm{S}\,\)は\(\,\mathrm{△ABC}\,\)の重心になることから長さがある程度分かってきます。

正四面体なので中線の長さは等く\(\,\mathrm{AR=RF=\color{red}{3\sqrt{3}}}\,\)であることから、
重心は中線を\(\,2:1\,\)に分けるので
　\(\hspace{4pt}\mathrm{AS}=\color{blue}{2\sqrt{3}}\)

\(\,\mathrm{△ARD}\,\)を抜き出してみてみます。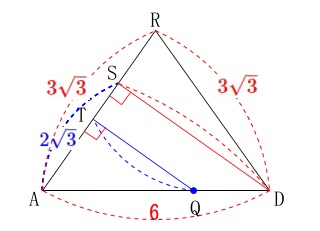直角三角形\(\,\mathrm{ADS}\,\)において三平方の定理から
　\(\begin{eqnarray}
\mathrm{AS^2+SD^2}&=&\mathrm{AD^2}\\
(2\sqrt{3})^2+\mathrm{SD^2}&=&6^2\\
\mathrm{SD^2}&=&36-12\\
&=&24\\
&=&\pm 2\sqrt{6}
\end{eqnarray}\)
長さなので
　\(\hspace{4pt}\mathrm{SD}=\color{red}{2\sqrt{6}}\)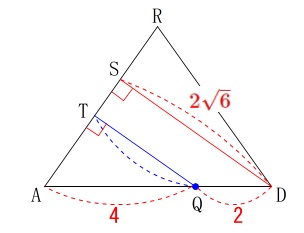線分\(\,\mathrm{AQ}\,\)と\(\,\mathrm{QD}\,\)の比から\(\,\mathrm{QT}=h\,\)は
　\(\begin{eqnarray}
\mathrm{SD:QT}&=&(\color{red}{4}+\color{red}{2}):\color{red}{4}\\
2\sqrt{6}:h&=&3:2\\
3\,h&=&2\sqrt{6}\times 2\\
h&=&\color{magenta}{\frac{4\sqrt{6}}{3}}
\end{eqnarray}\)
（これが求める立体の高さです。）

よって求める立体\(\,\mathrm{Q-APM}\,\)の体積\(\,V\,\)は
　\(\begin{eqnarray}
V&=&\frac{1}{3}\times S\times h\\
&=&\frac{1}{3}\times \color{magenta}{3\sqrt{3}}\times \color{magenta}{\frac{4\sqrt{6}}{3}}\\
&=&\underline{\underline{　4\sqrt{2}　}}(\mathrm{cm^3})
\end{eqnarray}\)

正四面体は対称性が多くあるのでよく問題に取り上げられます。
高さや垂線がどこに下りるかを見る問題が多いので、
この問題でも練習しておくと良いです。

ちなみに正四面体の体積の公式は、
各頂点から下りる垂線の長さを求める事がポイントになります。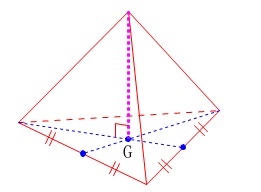底面と見る三角形（正三角形）の重心に下りるので覚えてきましょう。

以上です。

数学の解法は１つではないのでここで上げた方法でなくても良いですよ。

⇒　東京都公立高校入試数学の過去問と解答解説

東京都の問題は簡単とはいえませんが、
特別「変」と思える問題はありません。

他県の受験生も総復習に過去問に取り組むとかなり役に立つと思いますよ。