2023年(令和5年)度秋田県公立高校入試の数学の問題と解説（後半）

2023年(令和5年)度秋田県公立高校入試の数学の問題【後半】の解説です。
後半は第３問データの活用、第４問平面図形、第５問関数となります。
分量として時間配分的にどうかわかりませんが配点での後半としております。
第５問は選択問題となるので実際の試験では注意しておいて下さい。

2023年(令和5年)度秋田県公立高校入試の数学の問題

令和５年度秋田県公立高校入試の数学の問題です。

⇒　2023年(令和5年)度秋田県公立高校入試の数学の問題（後半）ＰＤＦ

ここでは第３問以降を載せておきました。
問題全体は前半のページにあるので確認して下さい。

2023年(令和5年)度秋田県公立高校入試の数学の解説【後半】

前半が長かったので後半はできるだけ簡単に説明しておきます。
基本的な用語の確認はしっかりやっておいて下さい。

第３問データの活用

問題文の読み取りはお任せしますが、
短いように見えてもヒストグラムなどはたくさんの情報を持っています。
データの読み取りは時間がかかるので意識しておくと良いです。

(1)
最頻値と中央値の読み取りです。

ヒストグラムで一番飛び出ているのが最頻値を含む階級、
中央値は３１人のデータなので１６番目のデータを含む階級にあります。

⇒　代表値とは？度数分布表の平均値,中央値の求め方と最頻値の答え方

問題は「最頻値が中央値よりも小さい」ヒストグラムを選びます。
最頻値は分かり易いので中央値に注目ですね。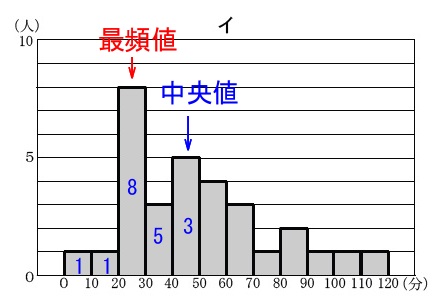左から小さい階級が並んでいるので、
最頻値を含む階級が中央値を含む階級より左にあるものです。
答え　\(\,\underline{　イ　}\,\)

全部を調べても良いですが、
１つ選べば良いので最頻値を含む階級が小さいものから調べると早いです。

(2)
「範囲」と「第１四分位数」を求めます。

３１人のクラスなのに３０人のデータとは？
という疑問はさておき、
小さい順に並べてくれているので助かりますね。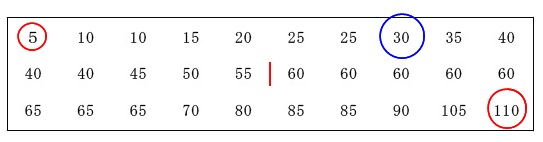データでは用語の意味を覚えていないと基本問題がとれません。

「範囲」は最大値から最小値を引けば出てきます。
　\(\hspace{10pt}110-5\\
=\underline{　105　}\)

次は「第１四分位数」です。
簡単にいうと第１四分位数は中央値より小さい側半分の中央値です。
ここでは３０人分のデータなので中央値は１５番目と１６番目の平均値になりますが、
１５個で分けられるので左１５個のデータの中央値を求めれば良いです。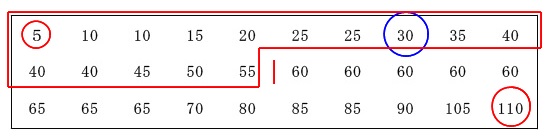つまり左から（小さい方から）８番目の値が第１四分位数です。

答え　\(\underline{　30　}\)

(3)
箱ひげ図の読み取りです。

①
正しいものを選びます。
可能性はあってもダメな場合が含まれる場合は正しいとはいいませんので、
必ずいえることでなければなりません。

着目する数値に印を入れておきます。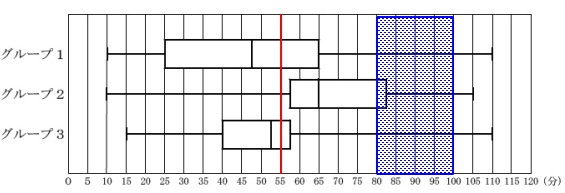
アとイは人数に関することなので四分位数ごとに人数を入れておくと分かり易いです。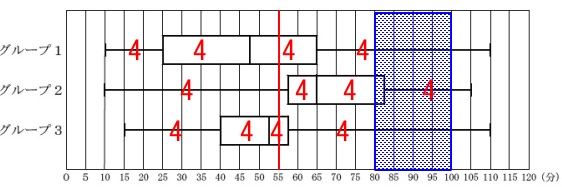４人ずつ四分位数ごとに入っていると考えれば、
アは正しいですが、イは違います。

ウはグループ１，３が必ずいるとはいえません。
（分布がひげの端に偏っているかもしれません。）

エはすべてのグループで最大値は１０５以上なので正しい。

答え　\(\,\underline{　ア\,,\,エ　}\,\)

箱ひげ図の読み取りは割と時間がかかりますので、
箱ひげ図の書き方を練習しておくと良いです。

②
散らばりの大きいグループを選び理由を書きます。

「散らばりぐあいが大きい」という意味は分かりにくいですが、
イメージでいうと図のようにデータが広い範囲で、
集中せずに存在していることをいいます。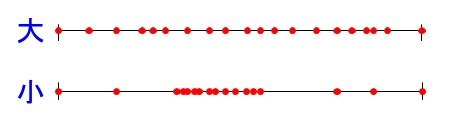計算で求める事はできますが、
高校に進んでからしっかり学んで下さい。

ここでは範囲と四分位範囲から判断します。

「範囲」「四分位範囲」ともに大きいので、
グループ１の散らばりぐあいが最も大きい。

答え　\(\,\underline{　ア　}\,\)

第４問平面図形

\(\,\large{4}\,\)
平面図形です。

合同の証明と逆と反例という用語の確認、
および図形の性質と方程式との融合があります。
(1)
合同の証明です。
　\(\hspace{10pt}\mathrm{△ACE}\)　≡　\(\mathrm{△BCF}\)

いつも通り図の中で終わらせておきましょう。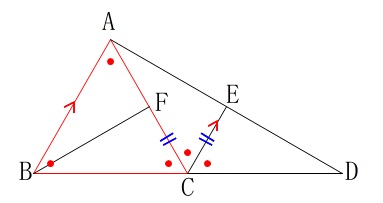　\(\,\mathrm{△ABC}\,\)が正三角形なので
　\(\hspace{10pt}\mathrm{AC=BC}　･･･①\)
　\(\hspace{10pt}\mathrm{∠ABC=∠BCA=∠BAC}=60°\)
また\(\,\mathrm{AB}\,\)∥\(\,\mathrm{EC}\,\)なので同位角と錯角が等しいことと合わせて
　\(\hspace{10pt}\mathrm{∠ACE=∠BAC=∠BCF}　･･･\color{red}{②}\)
仮定から
　\(\hspace{10pt}\mathrm{CE=CF}　･･･③\)

合同条件がそろいました。
「２辺とその間の角がそれぞれ等しい。」

合同条件がそろえば証明の書き方は好きにしていいです。

⇒　中学２年 平行と合同と証明の書き方ポイントまとめ

錯角から\(\,\color{red}{②}\,\)を言っていますが、
角度６０°が３つ並んでいることからでもいえます。

(2)
命題と逆についての真偽を述べます。

この命題は正しいです。
正しいときは「真（しん）」と言います。

逆とは、仮定と結論を入れかえたものです。
※
仮定と結論が見分けにくい命題もありますが、
「ならば」を自分で入れてしっくりくる前の部分が「仮定」だと思えば良いです。

詳しく知りたい人は高校の数学で本格的に習います。
⇒　命題と反例
（リンク先は当会の高校数学サイトです。）

ア
逆は命題の結論を仮定に、仮定を結論にすれば良いだけなので
　\(\color{black}{\fbox{　\(a+b=9\,\)ならば、\(a=3\,,\,b=6　\,　\)}}\)

必ず成り立つとはいえないときは正しくありません。
この逆は正しくありません。
「偽（ぎ）」といいます。

偽である場合は成り立たない例をあげます。
その例を「反例」と言いますが１つで良いです。

イ
どんなときに成り立ったない例をあげます。

反例：\(\color{black}{\fbox{　\(\,a=5\,,\,b=4\,\)　}}\)

１つで良いので何でも良いですよ。
（ただし、\(\,a\,,\,b\,\)は自然数という前提があります。）

(3)
直角三角形の斜辺の長さを求めます。

三平方の定理を利用しますが、
斜辺になるのがどの辺かわかりにくいです。

「辺\(\,\mathrm{AB}\,\)は辺\(\,\mathrm{BC}\,\)より\(\,\mathrm{2\,cm}\,\)長く」
　\(\hspace{4pt}\mathrm{AB}\,＞\,\mathrm{BC}\)
「辺\(\,\mathrm{BC}\,\)は辺\(\,\mathrm{CA}\,\)より\(\,\mathrm{7\,cm}\,\)長い」
　\(\hspace{4pt}\mathrm{BC}\,＞\,\mathrm{CA}\)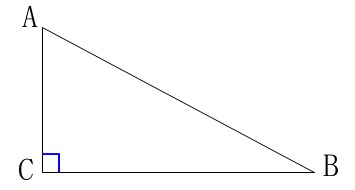一番長いのは辺\(\,\mathrm{AB}\,\)なので斜辺は\(\,\mathrm{AB}\,\)です。

求める\(\,\mathrm{AB}\,\)を\(\,x\,\)とするか、
最も短い\(\,\mathrm{AC}\,\)を\(\,x\,\)とするかは好きにしていいです。

注意が必要なので両方やってきます。

辺\(\,\mathrm{AB}\,\)を\(\,\color{red}{x}\,\)とすると、
　\(\hspace{4pt}\mathrm{BC}=\color{red}{x-2}\,,\,\mathrm{CA}=\color{red}{x-9}\)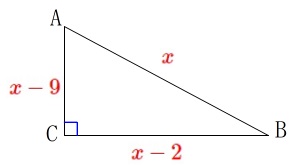三平方の定理から
　\(\begin{eqnarray}
\mathrm{CA^2+BC^2}&=&\mathrm{AB^2}\\
(x-9)^2+(x-2)^2&=&x^2\\
x^2-22x+85&=&0\\
(x-5)(x-17)&=&0\\
x&=&5\,,\,17
\end{eqnarray}\)

\(\,x=5\,\)のときは\(\,\mathrm{CA}\,\)の長さがマイナスになるのでダメです。

答え　\(\,\underline{　17　}\mathrm{cm}\,\)

この場合の注意点は長さ\(\,\mathrm{BC\,,\,CA}\,\)の表し方と、
辺の長さの条件です。

最も短い辺\(\,\mathrm{CA}\,\)を\(\,\color{blue}{x}\,\)とすると、
　\(\hspace{4pt}\mathrm{BC}=\color{blue}{x+2}\,,\,\mathrm{CA}=\color{blue}{x+9}\)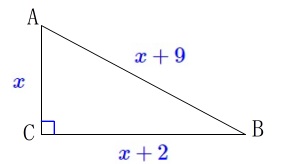三平方の定理から
　\(\begin{eqnarray}
\mathrm{CA^2+BC^2}&=&\mathrm{AB^2}\\
x^2+(x+2)^2&=&(x+9)^2\\
x^2-4x-32&=&0\\
(x+4)(x-8)&=&0\\
x&=&-4\,,\,8
\end{eqnarray}\)

長さなので\(\,x=8\,\)ですが、
求めるのは斜辺\(\,\mathrm{AB}\,\)なので
　\(\hspace{4pt}\mathrm{AB}=x+9=\underline{　17　}\mathrm{cm}\)

この場合は長さの表し方は分かり易いでしょう。
注意点は最後の答えの部分で求めるものが\(\,x\,\)ではないことです。

２次方程式の左辺が因数分解できるので方程式自体は問題ないでしょう。

第５問関数（図形的な性質との融合）

\(\,\large{5}\,\)
問題が２つあります。
指示された問題を解くので気をつけて下さい。

\(\,Ⅰ\,\)
２つの関数と定点があるので確認しておきましょう。
　㋐：\(\hspace{4pt}y=x^2\)
　㋑：\(\hspace{4pt}y=a\,x^2\,(\,0\,＜\,a\,＜\,1\,)\)
点\(\,\mathrm{A\,,\,B}\,\)は㋐上の点で、
　\(\hspace{4pt}\mathrm{A}\,\,(\,-1\,,\,1\,)\,,\,\mathrm{B}\,(\,2\,,\,4\,)\)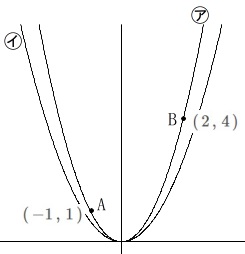(1)
２点を\(\,\mathrm{A\,,\,B}\,\)通る直線を求めます。

求める過程も書きますが余り気にせずいつもやっていることを書けば良いです。

２点
　\(\hspace{4pt}\mathrm{A}\,(\,-1\,,\,1\,)\)
　\(\hspace{4pt}\mathrm{B}\,(\,2\,,\,4\,)\)
を通る直線の傾き（変化の割合）は
　\(\hspace{4pt}\displaystyle \frac{4-1}{2-(-1)}\,=\,1\)
求める直線は
　\(\hspace{4pt}y=x+b\)
とおけて点\(\,\mathrm{B}\,\)を通るので
　\(\begin{eqnarray}
4&=&2+b\\
b&=&2
\end{eqnarray}\)
よって求める直線の式は
　\(\hspace{10pt}\underline{　y=x+2　}\)

もちろん点\(\,\mathrm{A}\,\)を通るとみても同じ\(\,y\,\)切片が出ます。

求める直線を\(\,y=ax+b\,\)とおいて
連立方程式を解いても良いですが、
傾きから出した方が早い、と思います。

(2)
線分の長さを求めます。

関数㋑において\(\displaystyle \,a=\frac{2}{3}\,\)のとき、
\(\,x\,\)座標が\(\,3\,\)のときの㋑上の点を\(\,\mathrm{C}\,\)とします。
　㋑：\(\hspace{4pt}\displaystyle y=\frac{2}{3}\,x^2\)
　\(\,\mathrm{C}：(\,3\,,\,6\,)\,\)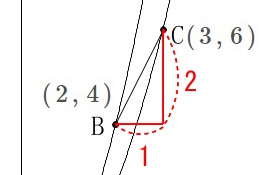点\(\,\mathrm{B}\,\)の座標は\(\,(\,2\,,\,4\,)\,\)なので、
線分\(\,\mathrm{BC}\,\)の長さは２点間の距離で三平方の定理から
　\(\begin{eqnarray}
\mathrm{BC}&=&\sqrt{1^2+2^2}\\
&=&\underline{　\sqrt{5}　}\,\mathrm{cm}
\end{eqnarray}\)

この問(2)では\(\,a\,\)が特定されていますが、
(3)ではまた未定となります。

(3)
条件によってできる四角形の面積が\(\,12\,\)になるときの\(\,a\,\)の値を求めます。

点\(\,\mathrm{P}\,\)の条件は㋐上で\(\,y\,\)の値が\(\,1\,\)なので、（\(\,x\,\)座標は正）
　\(\hspace{4pt}\mathrm{P}\,(\,1\,,\,1\,)\)
点\(\,\mathrm{Q}\,\)は\(\,y\,\)座標が\(\,4\,\)で点\(\,\mathrm{B}\,\)と同じなので、
四角形\(\,\mathrm{APBQ}\,\)は台形です。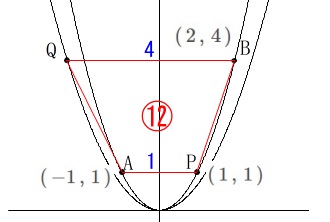具体的な面積があるので方法はいくつか出てくると思います。

ここでは点\(\,\mathrm{Q}\,\)の\(\,x\,\)座標を\(\,t\,\)とおいて機械的に解いておきます。
点\(\,\mathrm{Q}\,\)の\(\,x\,\)座標を\(\,t\,\)とすると\(\,y\,\)座標は\(\,4\,\)なので
　\(\hspace{4pt}\mathrm{Q}\,(\,t\,,\,4\,)\)

このとき\(\,\mathrm{BQ}\,\)の長さは\(\,x\,\)座標の差で
　\(\hspace{4pt}\mathrm{BQ}\,=\,\color{red}{2-t}\)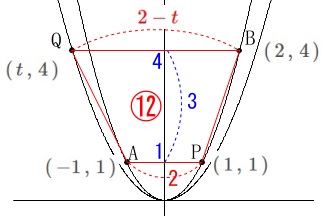台形の高さは\(\,y\,\)座標の差で\(\,\color{blue}{3}\,\)なので
　\(\begin{eqnarray}
\frac{(\,\color{red}{2-t}\,)+\color{red}{2}}{2}\times \color{blue}{3}&=&12\\
4-t&=&8\\
t&=&-4
\end{eqnarray}\)

よって点\(\,\mathrm{Q}\,\)の座標は\(\,(\,-4\,,\,4\,)\,\)となり、
これは関数㋑\(\,y=ax^2\,\)上の点なので
　\(\begin{eqnarray}
4&=&a\times (-4)^2\\
a&=&\underline{\underline{　\frac{1}{4}　}}
\end{eqnarray}\)

\(\,y\,\)軸で台形を分けると右側は具体的に求まります。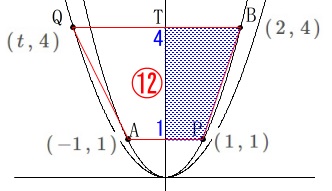\(\,\mathrm{QT}\,\)の長さを求めても良いですが、
座標を文字で設定した方が楽なので少し慣れておくと良いですね。
（座標か長さかで変わってくるので符号には気をつけておきましょう。）

\(\,Ⅱ\,\)
関数です。
選択問題で受験生はどちらかしか解きませんが、
これを見ている人は両方見ていると思うので条件の読み取りと、
ポイントだけを抑えて解説は\(\,Ⅰ\,\)より簡単に済ませます。

２次関数㋐と１次関数㋑があります。
　㋐：\(\hspace{4pt}\displaystyle y=\frac{1}{2}\,x^2\)
　㋑：\(\hspace{4pt}y=-x+4\)
２点\(\,\mathrm{A\,,\,B}\,\)は定点です。
　\(\hspace{4pt}\mathrm{A}\,(\,-4\,,\,8\,)\)
　\(\hspace{4pt}\mathrm{B}\,(\,2\,,\,2\,)\)
２点とも㋐㋑上の点（交点）であることを確認しておきましょう。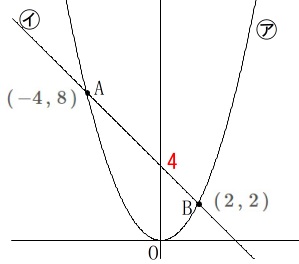点\(\,\mathrm{P}\,\)は㋐上の点で\(\,x\,\)座標が\(\,t\,\)です。
　\(\hspace{4pt}\displaystyle \mathrm{P}\,\left(\,t\,,\,\frac{1}{2}\,t^2\,\right)\)
点\(\,\mathrm{Q}\,\)は点\(\,\mathrm{P}\,\)と\(\,x\,\)座標が同じで㋑上の点です。
　\(\hspace{4pt}\displaystyle \mathrm{Q}\,(\,t\,,\,-t+4\,)\)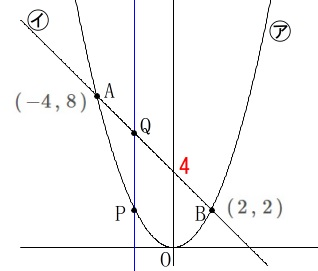ここからは問題ごとに条件が変わります。

(1)
点\(\,\mathrm{P}\,\)の\(\,x\,\)座標が\(\,-2\,\)のとき２点\(\,\mathrm{A\,,\,P}\,\)を通る直線の式を求めます。

求める直線は\(\,t=-2\,\)なので２点
　\(\hspace{4pt}(\,-4\,,\,8\,)\)
　\(\hspace{4pt}(-2\,,\,2\,)\)
を通るので
　\(\hspace{4pt}\underline{　y=-3x-4　}\)

直線の式を求める事は説明いらないと感じるくらい当たり前のことです。
ただ、これを解答にすると減点されると思うので、
\(\,Ⅰ\,\)で説明しているくらいは求める過程を書いた方が良いです。

⇒　変化の割合とは？1次関数の求め方と直線の方程式との違い

１つの関数の問題の中で何本も直線の式を求めることは良くあります。
少し時間をかけても短時間でも求められるように練習しておいた方が良いですね。

(2)
点\(\,\mathrm{P}\,\)は固定されていません。
　\(\hspace{4pt}\displaystyle \mathrm{P}\,\left(\,t\,,\,\frac{1}{2}\,t^2\,\right)\,\)
\(\,t\,\)の範囲は\(\,-4\,＜\,t\,＜\,2\,\)です。

①
\(\,\mathrm{AQ}=\color{red}{5\sqrt{2}}\,\)の\(\,\mathrm{P}\,\)の\(\,x\,\)座標\(\,t\,\)を求めます。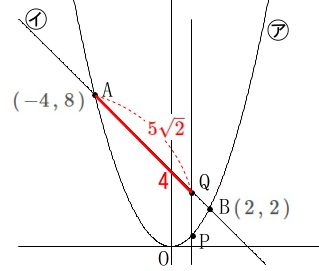点\(\,\mathrm{P}\,\)が\(\,\mathrm{A\,,\,B}\,\)の間にあることと\(\,\mathrm{AB}\,\)の長さからだいたいの位置は分かりますが、
機械的に求めておきます。

点\(\,\mathrm{Q}\,\)の座標は\(\,(\,t\,,\,-t+4\,)\,\)です。
２点\(\,\mathrm{AQ}\,\)の距離が\(\,5\sqrt{2}\,\)なので
　\(\begin{eqnarray}
(t+4)^2+(\color{red}{4+t})^2&=&(5\sqrt{2})^2\\
2(t^2+8t+16)&=&50\\
t^2+8t+16&=&25\\
t^2+8t-9&=&0\\
(t-1)(t+9)&=&0\\
t&=&1\,,\,-9
\end{eqnarray}\)
\(\,-4\,＜\,t\,＜\,2\,\)なので
　\(\hspace{10pt}t=\underline{　1　}\)

２点\(\,\mathrm{A\,,\,Q}\,\)は
　\(\hspace{4pt}\mathrm{A}\,(\,-4\,,\,8\,)\)
　\(\hspace{4pt}\mathrm{Q}\,(\,t\,,\,-t+4\,)\)
なので
　\((\,x\,座標の差\,)=t+(-4)=t+4\)
　\((\,y\,座標の差\,)=(-t+4)-8=\color{red}{-t-4}\)
とした人も三平方の定理で平方するので同じです。

(3)
条件に点\(\,\mathrm{R}\,,\,\mathrm{S}\,\)が加わり、
四角形\(\,\mathrm{PQSR}\,\)の面積が\(\,30\,\)になるときの\(\,t\,\)の値を求めます。

点\(\,\mathrm{R}\,,\,\mathrm{S}\)の位置を読み取れれば問題ないでしょう。
「点\(\,\mathrm{R}\,\)は㋑上の点」です。
条件は\(\,x\,\)座標は\(\,2\,\)より大きく
　\(\hspace{4pt}\mathrm{BR=BQ}\)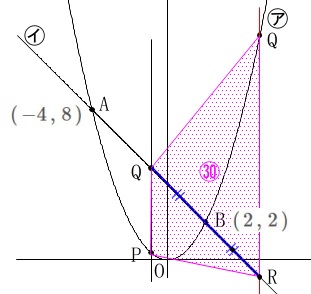点\(\,\mathrm{R}\,,\,\mathrm{S}\,\)は\(\,x\,\)座標が同じなので四角形\(\,\mathrm{PQSR}\,\)は台形となります。
具体的な面積があるので色々考えたくなりますが、
それぞれの座標を\(\,t\,\)で表し機械的に処理しましょう。

最初にある条件から
　\(\hspace{4pt}\displaystyle \mathrm{P}\,\left(\,t\,,\,\frac{1}{2}\,t^2\,\right)\)
　\(\hspace{4pt}\displaystyle \mathrm{Q}\,(\,t\,,\,-t+4\,)\)
条件\(\,\mathrm{BR=BQ}\,\)なので
　\(\hspace{4pt}\mathrm{R}\,(\,4-t\,,\,t\,)\)
　\(\hspace{4pt}\displaystyle \mathrm{S}\,\left(\,4-t\,,\,\frac{1}{2}\,(4-t)^2\right)\)※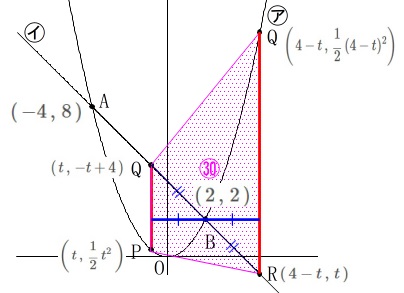
点\(\,\mathrm{Q\,,\,R}\,\)の\(\,x\,\)座標の表し方ですが、
\(\,\mathrm{B}\,\)と\(\,\mathrm{Q}\,\)の\(\,x\,\)座標の差の分\(\,\mathrm{R}\,\)の\(\,x\,\)座標は\(\,\mathrm{B}\,\)より大きい。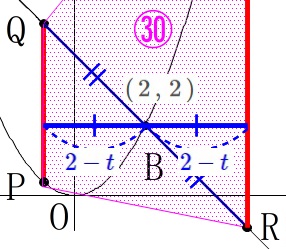\(\,\mathrm{B}\,\)より\(\,\color{blue}{2-t}\,\)大きくなるので、
点\(\,\mathrm{Q\,,\,R}\,\)の\(\,x\,\)座標は
　\(\hspace{4pt}2+(2-t)=4-t\)

この座標をみた時点では台形の面積にするとすごくややこしくなりそうです。
ただ、
突っ走るしかないときもあります。

一気に進めても良いのですが部分的に長さを出しておきます。
　\(\begin{eqnarray}\displaystyle \mathrm{PQ}&=&(-t+4)-\frac{1}{2}\,t^2\\
&=&-\frac{1}{2}\,t^2-t+4
\end{eqnarray}\)
　\(\begin{eqnarray}
\mathrm{RS}&=&\frac{1}{2}(4-t)^2-t\\
&=&\frac{1}{2}(t^2-8t+16)-t\\
&=&\frac{1}{2}\,t^2-4t+8-t\\
&=&\frac{1}{2}\,t^2-5t+8
\end{eqnarray}\)
このとき上底と下底の和は
　\(\begin{eqnarray}
\color{red}{\mathrm{PQ+RS}}&=&\left(-\frac{1}{2}\,t^2-t+4\,\right)+\left(\,\frac{1}{2}\,t^2-5t+8\,\right)\\
&=&\color{red}{-6t+12}
\end{eqnarray}\)
高さとなる\(\,\mathrm{P\,,\,R}\,\)の\(\,x\,\)座標の差\(\,h\,\)は
　\(\hspace{4pt}\color{blue}{h}=\color{blue}{2(2-t)}\)
台形の面積が\(\,30\,\)なので
　\(\begin{eqnarray}
30&=&\frac{\color{red}{\mathrm{PQ+RS}}}{2}\times \color{blue}{h}\\
&=&\frac{\color{red}{-6t+12}}{2}\times \color{blue}{2(2-t)}\\
&=&6(-t+2)(2-t)\\
5&=&t^2-4t+4\\
0&=&t^2-4t-1
\end{eqnarray}\)

因数分解できないので解の公式です。
　\(\hspace{4pt}\displaystyle t=2\pm \sqrt{5}\)
\(\,t\,\)の範囲に条件があるので絞れます。
　\(\hspace{4pt}t=\underline{　2-\sqrt{5}　}\)

２次方程式の処理は自分でしておいて下さい。

⇒　２次方程式の解の公式二通りの求め方と便利な公式と文章題の解き方

上手い解法を見つけても、
泥くさく解いても同じ５点です。

以上です。

⇒　2023年(令和5年)度秋田県公立高校入試の数学の問題と解説（前半）

配点の（ほぼ）半分で前半と後半に分けました。

⇒　秋田県の公立高校入試数学の過去問と解説

偏りの少ない出題範囲のバランスの良さから傾向は大きくは変わらないと思います。
実際の試験で時間配分をどうするかはご自身で判断するしかありませんが、
前半の広い範囲の基礎を確実に抑えているかどうかで後半に対応できるかが決まりそうですね。