２０２３年(令和５年)度群馬県公立高校入試【前期選抜】の数学の問題と解説です。
前期入試の問題ですので問題数も少なく基本問題中心なのでそれ程詳しい説明も必要ないでしょう。
シンプルで数値もきれいな問題なので基本をしっかり抑えてきた人にはそれ程時間もかからないです。
２０２３年(令和５年)度群馬県公立高校入試【前期選抜】の数学の問題
問題は大問で４問あります。
⇒ ２０２３年(令和５年)度群馬県公立高校入試【前期選抜】の数学の問題ＰＤＦ
シンプルに基本を問われますがある程度の作業は必要です。
２０２３年(令和５年)度群馬県公立高校入試【前期選抜】の数学の解説
会員に向けてですが、
『覚え太郎』と基本レポートを軽く一周してから取り組むと良いです。
集中すれば制限時間の半分くらいあれば終わると思います。
第１問
\(\,\large{1}\,\)
小問が７問あります。
(1)計算問題６題です
①
\(\hspace{10pt}-6+4\\
=\underline{ -2 }\)
正負の数の加減は数直線上でみれば明らかですね。
②
\(\hspace{10pt}5\times (-3)^2\\
=5\times 9\\
=\underline{ 45 }\)
計算順序、符号に注意すれば問題なし。
③
\(\hspace{10pt}2\times (-2a)\\
=\underline{ -4a }\)
ただの数値も文字式も計算方法は同じです。
④
\(\hspace{10pt}3x+4y-(x-y)\\
=3x+4y-x+y\\
=\underline{ 2x+5y }\)
急いで２行目を省略しないようにしましょう。
制限時間短くして焦らせたのは誰？
違う違う。
焦らせているのではなく集中して解いていけばそれくらいの時間以内で終わるってだけです。
⑤
\(\hspace{10pt}(12a-8b)\div 4\\
=\underline{ 3a-2b }\)
係数が割り切れるのがすぐに分かるから分数にしていません。
⑥
\(\hspace{10pt}\displaystyle \frac{9}{\sqrt{3}}+\sqrt{12}\\
\displaystyle =\frac{9\sqrt{3}}{3}+2\sqrt{3}\\
=3\sqrt{3}+2\sqrt{3}\\
=\underline{ 5\sqrt{3} }\)
無理数計算は慣れの違いで暗算できる段階が変わるので、
２行目を省略した人もいるでしょう。
分母の有理化、素因数部分はていねいにやった方がミスは確実に減ります。
(2)
文字式の展開です。
\(\hspace{10pt}(x-1)(y+3)\\
=\underline{ xy+3x-y-3 }\)
展開の順序によっては
\(\hspace{10pt}(x-1)(y+3)\\
=xy-y+3x-3\)
とした人もいるでしょう。
後々を考えると前から分配しておきたいですがどちらでも良いです。
（答えとしては前者が適しています。）
(3)
因数分解です。
\(\hspace{10pt}x^2-2x\color{red}{-15}\)
定数項に着目しましょう。
かけて\(\,15\,\)になるのは
\(\color{black}{\fbox{\(\,1\times 15\,\)}}\)、\(\color{black}{\fbox{\(\,3\times 5\,\)}}\)
なので符号を考えて
\(\hspace{10pt}x^2-2x-15\\
=\underline{ (x+3)(x-5) }\)
(4)
回転移動なので中心は移動しません。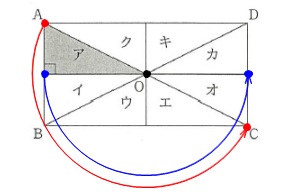
回転する図形は三角形ですが、
一つひとつの点が移動して成り立ちます。
答え \(\,\underline{ オ }\,\)
\(\,180°\,\)の回転なので時計回りでも同じです。
(5)
反比例の関数を求めます。
\(\hspace{10pt}\displaystyle y=\frac{a}{x}\)
比例定数を決めましょう。
\(\begin{eqnarray}
-3&=&\frac{a}{-4}\\
a&=&12
\end{eqnarray}\)
答え \(\hspace{4pt}\displaystyle \underline{\underline{ y=\frac{12}{x} }}\)
比例定数は
\(\begin{eqnarray}a&=&x\,y\\
&=&(-4)\times (-3)\\
&=&12
\end{eqnarray}\)
でも求まりますが問題の求めているのは「\(\,y\,\)を\(\,x\,\)の式で」なので、
\(\hspace{4pt}xy=12\,\)としないように注意しましょう。
(5)
連立方程式を解きます。
\( \begin{cases}
\hspace{4pt} 3x+2y=-1 ･･･①\\
\hspace{4pt} y=x-3 ･･･②
\end{cases}\)
加減法でも良いですが代入法の方が楽そうです。
\(\,②\,\)を\(\,①\,\)に代入して
\(\begin{eqnarray}
3x+2(x-3)&=&-1\\
3x+2x-6&=&-1\\
5x&=&5\\
x&=&1
\end{eqnarray}\)
②に戻すと
\(\begin{eqnarray}
y&=&x-3\\
&=&(1)-3\\
&=&-2
\end{eqnarray}\)
答え \(\,\underline{ x=1\,,\,y=-2 }\,\)
\(\,①\,\)に戻して満たすか確認すれば計算ミスの確認ができます。
\(\hspace{4pt}3(1)+2(-2)=-1\)
(7)
角度を求めます。
求めるのは内角ですが、
多角形は和が一定なので外角で進めます。
五角形の４つの外角の和が
\(\hspace{10pt}80°+80°+60°+70°=290°\)
なのでもう一つの外角は
\(\hspace{10pt}360°-290°=\color{red}{70°}\)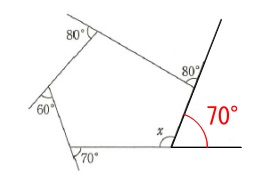
よって求める\(\,x\,\)の角度は
\(\hspace{10pt}∠x=180°-70°=\underline{ 110° }\)
外角の和は\(\,360°\,\)と一定なのでそれ以上大きな計算がでません。
もちろん内角の和から計算しても答えは同じです。
第２問
\(\,\large{2}\,\)
\(\,\large{1}\,\)同様に小問集合で\(\,4\,\)問あります。
(1)
グラフから「傾き」と「\(\,y\,\)切片」の符号をみます。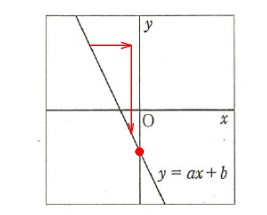
傾き\(\,a\,\)は負で\(\,y\,\)切片\(\,b\,\)も負です。
\(\hspace{10pt}a\,＜\,0\,,\,b\,＜\,0\)
これから和と積は
\(\hspace{4pt}a+b\,＜\,0\,,\,ab\,＞\,0\,\)
答え \(\,\underline{ ウ }\,\)
一般的に成り立つことなので例えば、
グラフの条件が同じになる
\(\hspace{10pt}y=-2x-3\)
などから計算しても答えは探せます。
(2)
回転体の体積を求めます。
※
長さの単位は\(\,\mathrm{cm}\,\)です。
簡単に見取り図を書けば分かりますが円すいです。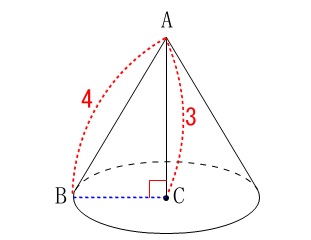
底面の円の面積が必要になります。
三平方の定理から
\(\begin{eqnarray}
\mathrm{BC^2+AC^2}&=&\mathrm{AB^2}\\
\mathrm{BC^2}+3^2&=&4^2\\
\mathrm{BC^2}&=&7\\
\mathrm{BC}&=&\pm \sqrt{7}
\end{eqnarray}\)
長さなので\(\hspace{4pt}\mathrm{BC}=\sqrt{7}\)。
これが底面の円の半径だから求める回転体の体積\(\,V\,\)は
\(\begin{eqnarray}
V&=&\frac{1}{3}\times \pi\,(\sqrt{7})^2\times 3\\
&=&\underline{ 7\,\pi }\,(\mathrm{cm^3})
\end{eqnarray}\)
すい体なので\(\displaystyle \,\frac{1}{3}\,\)をかけるのを忘れないようにしましょう。
(3)
相対度数分布表の読み取りです。
度数合計や比較する階級は問題を読んで下さい。
相対度数は同じなので度数合計が多い方が度数が多いのはすぐに分かりますが、
度数の違いも求めるので計算しなければなりません。
\(\,\mathrm{A}\,\)中学校：\(\hspace{4pt}80\times 0.15\,=\,12\,(\,人\,)\)
\(\,\mathrm{B}\,\)中学校：\(\hspace{4pt}100\times 0.15\,=\,15\,(\,人\,)\)
答え \(\,\underline{ \mathrm{B} }\,\)中学校の方が\(\,\underline{ 3 }\,\)人多い。
⇒ 度数分布表とは？階級の幅と階級値および累積度数とヒストグラム
相対度数についても追記していたと思うので確認しておいて下さい。
データは用語の意味を覚えておかないとどうしようもないです。
(4)
１次方程式です。
定価を\(\,x\,\)として合計金額を計算すると、
\(\,\mathrm{A}\,\)店は１割引なので
\(\hspace{10pt}\displaystyle 30\,x\times \frac{90}{100}\,\left(=30\,x\times \frac{9}{10}\right)\)
\(\,\mathrm{B}\,\)店は\(\,1\,\)枚が無料になるので\(\,29\,\)枚分で
\(\hspace{10pt}29\,x\)
\(\,\mathrm{A}\,\)店の方が\(\,1200\,\)円安かったので（\(\,\mathrm{B}\,\)店の金額が大きい）
\(\begin{eqnarray}
30\,x\times \frac{90}{100}+1200&=&29\,x\\
27\,x+1200&=&29\,x\\
x&=&\underline{ 600 }(\,円\,)
\end{eqnarray}\)
定価を求めるので答えは整数で出てくるはず。
１割をどう取るかはどっちでも良いので後は日本語を加えて解答とすれば良いです。
等しくするために加えるか引く１２００円はどちらかは分かりますよね。
第３問
\(\,\large{3}\,\)
１次関数です。
グラフが与えられているので図\(\,\mathrm{Ⅰ}\,\)から考えことはありません。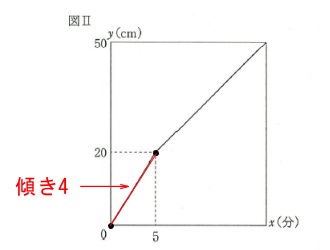
(1)
入れはじめてから５分までは傾きが\(\,\displaystyle \frac{20}{5}=4\,\)なので
関数は\(\,y=4\,x\,\)となっています。
３分後\(\,(x=3)\,\)の水面の高さ\(\,y\,\)は
\(\hspace{10pt}y=4\times (3)=\underline{ 12 }\,(\,\mathrm{cm}\,)\)
入れ初めから5分後までは比例なので
\(\hspace{10pt}\displaystyle 20\times \frac{3}{5}=12\,(\,\mathrm{cm}\,)\)
でも良いです。
(2)
今度は入れはじめてからの時間を求めます。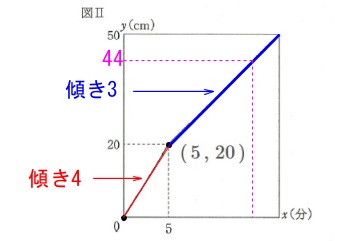
５分後からは水面の上がる速さが\(\displaystyle \frac{3}{4}\,\)倍に変わっています。
つまり速さは毎分\(\,\mathrm{3\,cm}\,\)になっているので、
\(\,5\,\)分後\(\,\mathrm{20\,cm}\,\)なので\(\,(\,5\,,\,20\,)\,\)を通ることから
関数は\(\,y=3x+5\,\)と表せます。
直線、特に１次関数の求め方は一日かけてでも必ず覚えておきましょう。
水面の高さが\(\,y=44\,\)になるのは入れはじめてから
\(\begin{eqnarray}
44&=&3\,x+5\\
x&=&\underline{ 13 }\,(\,分後\,)
\end{eqnarray}\)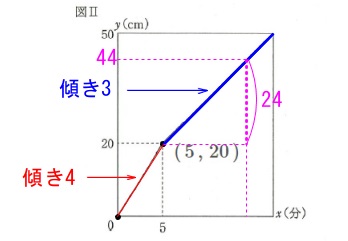
入れはじめて\(\,5\,\)分後からの速さが毎分\(\,3\,\mathrm{cm}\,\)と分かれば、
\(\,5\,\)分後の\(\,\mathrm{20\,cm}\,\)から\(\,\mathrm{24\,cm}\,\)上昇すれば良いので
\(\hspace{4pt}\displaystyle \frac{24}{3}=8\,(\,分後\,)\)
の入れはじめてから\(\,13\,\)分後だと求める事もできます。
ここでは整数で計算できるのでどちらでも良いですが、
関数で処理する方がいろいろと対応し易いです。
第４問
\(\,\large{4}\,\)
平面図形です。
条件は問題で読み取れば良いですが、
ここでもまとめと駅ます。
条件
線分\(\,\mathrm{AB}\,\)は円\(\,\mathrm{O}\,\)の直径。
\(\hspace{4pt}\mathrm{BC=CA}\)
\(\hspace{4pt}\mathrm{∠BCA}=90^{\circ}\)
四角形\(\,\mathrm{BDEC}\,\)は正方形。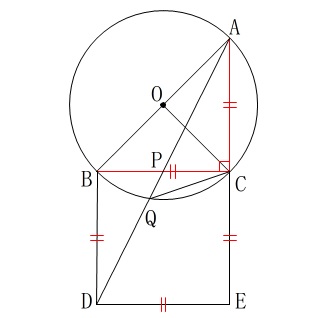
正方形や直角二等辺三角形があるので分かり易いです。
(1)
角度を求めます。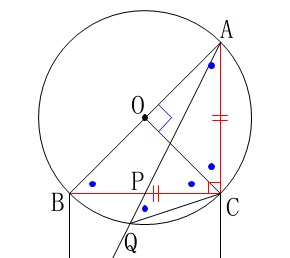
三角形\(\,\mathrm{ABC}\,\)が直角二等辺三角形なので底角が等しく、
円周角が等しいことから
\(\hspace{10pt}\mathrm{∠AQC=∠ABC}=\underline{ 45 }^{\circ}\)
\(\,\mathrm{△AOC}\,\)も直角二等辺三角形で\(\,\mathrm{∠AOC=90°}\,\)なので、
弧\(\,\mathrm{AC}\,\)の円周角は
\(\hspace{10pt}\mathrm{∠AQC}=\underline{ 45 }°\)
という方向でも大して差はありません。
分かることを書き出して行けば自ずと出てきます。
(2)
相似の証明です。
\(\,\mathrm{△ABP}\,\)∽\(\,\mathrm{△CQP}\,\)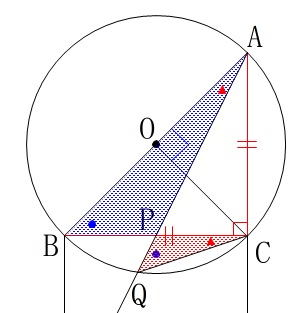
円周角が等しいことを２回をいうか、
円周角と対頂角が等しいことををいえば良いので証明は省略しておきます。
いずれにしても「２組の角がそれぞれ等しい。」が相似条件です。
⇒ 中学の図形証明問題(合同･相似)の解き方と証明の書き方ポイント
図の中で示せないことは文章では示せません。
(3)
条件が加わり、長さを求めます。
\(\hspace{10pt}\mathrm{BD}=2\)
（長さの単位は\(\,\mathrm{cm}\,\)ですが省略します。）
他の条件はそのまま引き継いでいます。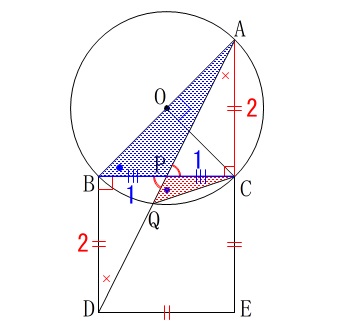
合同な三角形までは図に示しておきました。
\(\,\mathrm{△DBP}\,\)≡\(\,\mathrm{△ACP}\,\)
このことから
\(\hspace{10pt}\mathrm{BP=CP}=\color{blue}{1}\)
ここで(2)の相似を使いたいですね。
必要な辺の長さを求めておきましょう。
直角二等辺三角形の斜辺なので
\(\hspace{10pt}\mathrm{AB}=\color{magenta}{2\sqrt{2}}\)
三平方の定理から
\(\begin{eqnarray}
\mathrm{AP^2}&=&\mathrm{AC^2+CQ^2}\\
&=&2^2+1^2\\
&=&5\\
\mathrm{AP}&=&\pm \sqrt{5}
\end{eqnarray}\)
長さだから正の数で
\(\hspace{10pt}\mathrm{AP}=\color{blue}{\sqrt{5}}\)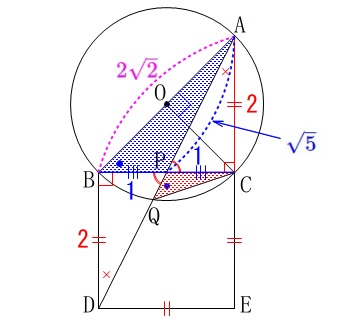
(2)から
\(\,\mathrm{△ABP}\,\)∽\(\,\mathrm{△CQP}\,\)
なので
\(\begin{eqnarray}
\mathrm{AB:AP}&=&\mathrm{CQ:CP}\\
\color{magenta}{2\sqrt{2}}:\color{blue}{\sqrt{5}}&=&\mathrm{CQ}:1\\
\sqrt{5}\times \mathrm{CQ}&=&2\sqrt{2}\\
\mathrm{CQ}&=&\frac{2\sqrt{2}}{\sqrt{5}}\\
&=&\underline{\underline{ \frac{2\sqrt{10}}{5} }}(\,\mathrm{cm}\,)
\end{eqnarray}\)
以上です。
レポートでやっているいつも通りの手順で作業をすれば問題ないでしょうが、
解説が不足しているかもしれません。
気になるところがあればご連絡ください。
後期選抜の問題もあるのでみておくと良いです。
ここは解説ページですので対策は各自にお任せしますが、
どちらかといえば後期の問題に慣れておくことをお勧めします。
クラブ活動で忙しい！
塾に通っているのに数学が苦手！
数学の勉強時間を減らしたい！
数学の勉強方法が分からない！
その悩み、『覚え太郎』が解決します！！！
