2023年(令和５年)度群馬県公立高校入試数学【後期】の問題と解説

2023年(令和５年)度群馬県公立高校入試【後期選抜】数学の問題と解説です。
例年通り分野の偏りはないので中学数学全体からの出題になっています。
軽めですが規則性の問題もあるので基本の確認にすると良いですね。
解説は過去の解説よりはあっさりとしておきますのでさらっと読んで下さい。

2023年(令和５年)度群馬県公立高校入試数学【後期】の問題

令和５年度後期選抜の問題\(\,\mathrm{PDF}\,\)です。

⇒　2023年(令和５年)度群馬県公立高校入試数学【後期】の問題ＰＤＦ

大問６問で構成されています。

2023年(令和５年)度群馬県公立高校入試数学【後期】の解説

平均点などは別ページで確認してください。
群馬県の過去問解説まとめページに記載してあります。

早速進めて行きましょう。

第１問小問集合

\(\,\large{1}\,\)
(1)計算問題です。
ポイントは前期選抜と同じなので確認しておいてください。
①
　\(\hspace{10pt}2-(-4)\\
=2+4\,=\underline{　6　}\)
②
　\(\hspace{10pt}\displaystyle 6a^2\times \frac{1}{3}a\\
=\underline{　2a^3　}\)
③
　\(\hspace{10pt}\displaystyle -2(3x-y)+2x\\
=-6x+2y+2x\\
=\underline{　-4x+2y　}\)

(2)方程式を解きます。
①
　\(\begin{eqnarray}
6x-1&=&4x-9\\
2x&=&-8\\
x&=&\underline{　-4　}
\end{eqnarray}\)
移項には気をつけてください。

②　\(\hspace{4pt}x^2+5x+3=0\)
方程式の右辺が\(\,0\,\)で左辺が因数分解できないので解の公式です。
　\(\begin{eqnarray}
x&=&\frac{-5\pm \sqrt{5^2-4\cdot 1\cdot 3}}{2\times 1}\\
&=&\frac{-5\pm \sqrt{25-12}}{2}\\
&=&\underline{\underline{　\frac{-5\pm \sqrt{13}}{2}　}}
\end{eqnarray}\)

※
解の公式の利用計算中の「\(\,\cdot\,\)」は掛け算の意味です。

(3)
数の大小ですのでやることは決まっています。
絶対値はアから順に
　\(\hspace{4pt}\displaystyle 3.0　\,,\,　5.0　\,,\,　2.5　\,,\,　2.1\)

最も小さいのは\(\,\underline{　エ　}\,\)。

⇒　正の数負の数の大小を比較する数直線利用の練習問題と絶対値の意味

絶対値の意味は知っていることが前提です。
その後に数の世界統一ですね。

(4)比例定数の決定ですね。
　\(\begin{eqnarray}
-12&=&a\times (-2)^2\\
4a&=&-12\\
a&=&\underline{　-3　}
\end{eqnarray}\)

比例でも反比例でも「比例定数」というので忘れないで下さい。

(5)
角度を求めます。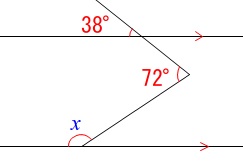平行線で作られる角なので、
同位角、錯角が等しいことを利用する方向で考えれば間違いありません。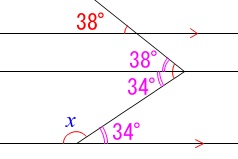すべての角度が分かるので答えが見えてくるまで書き出すと良いです。
　\(\begin{eqnarray}
∠x+34°&=&180°\\
∠x&=&\underline{　146°　}
\end{eqnarray}\)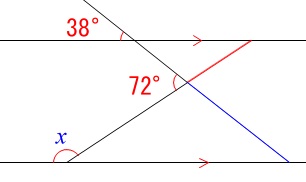線分の延長でも良いですよ。
方法は何でもいいので分かる角度を書き出して行くことですね。

(6)
会員ならサービス問題です。
　\(\begin{eqnarray}
a&=&2+\sqrt{5}\\
a-2&=&\sqrt{5}
\end{eqnarray}\)
両辺を平方すると
　\(\begin{eqnarray}
(a-2)^2&=&5\\
a^2+4a+4=&\underline{　5　}
\end{eqnarray}\)

あからさまな与式（求値式）から進めると
　\(\hspace{10pt}a^2-4a+4=(a-2)^2　･･･①\)
ここで条件式は
　\(\begin{eqnarray}
a&=&2+\sqrt{5}\\
a-2&=&\sqrt{5}　･･･②
\end{eqnarray}\)
\(\,②\,\)を\(\,①\,\)に代入すると
　\(\hspace{10pt}(a-2)^2=(\sqrt{5})^2=\underline{　5　}\)

もちろん、直接代入しても決して厳しい計算ではありません。
　\(\begin{eqnarray}
a^2-4a+4&=&(2+\sqrt{5})^2-4(2+\sqrt{5})+4\\
&=&4+4\sqrt{5}+5-8-4\sqrt{5}+4\\
&=&5
\end{eqnarray}\)
求値としては間違いではありませんが、
単なる計算問題として出題しているとは思えません。

(7)
確率を求めるので樹形図です。
元に戻さないので全部で１２通りしかありません。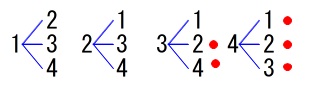\(\,32\,\)以上になるのは\(\,5\,\)通りなので
　\(\hspace{10pt}\displaystyle \underline{\underline{　\frac{5}{12}　}}\)

(8)
「すべて」とありますが立方体の１辺に垂直な面は２つあります。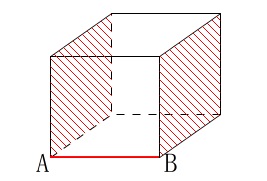１つはアであることは容易に分かるでしょう。
もう一つも展開図を組み立てて立方体のどの位置に来るかをみていけば良いだけです。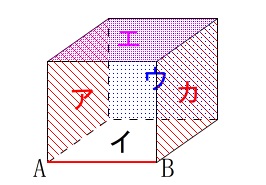イとウとエとオでぐるっと回るので、
手前の面がオで、アの向かいにある平行な面はカです。

答え　\(\,\underline{　ア\,,\,カ　}\,\)

面アに平行な面オを探すのは頂点をみていけば良いのですが、
長くなるので簡単に説明すると、
頂点は二マスの対角線移動で立方体の反対になります。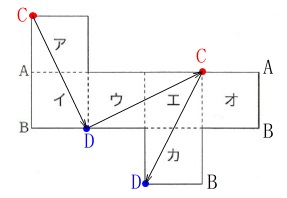例えば\(\,\mathrm{\color{red}{C}}\,\)の対角線の先は\(\,\mathrm{\color{blue}{D}}\,\)です。
２回繰り返すと元に戻るので、
それぞれの頂点がどこと重なるのかが分かります。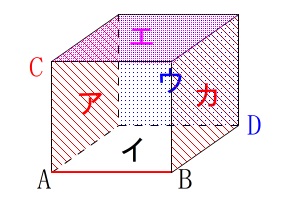そんなに時間をかけなくても良いので、
頂点に記号をつけて移動させてみて下さい。
展開図のすべての点がどこで重なるか分かります。
（会員は『超え太郎』－空間図形No.２８です。）

(9)この問も正しいといえるものを「すべて」選びます。
ここは探すのでなく、すべてみていく必要があります。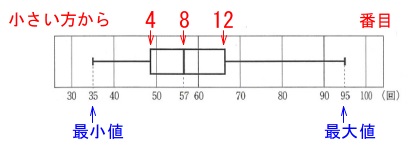箱ひげ図は最近出題しているところが多いので、
繰り返しになるので詳しい説明は必要ないでしょう。
データを小さい順に並べたとき、
　\(○○○\color{blue}{●}○○○\color{red}{●}○○○\color{magenta}{●}○○○\)
第１四分位数は\(\,\color{blue}{●}\,\)、第３四分位数は\(\,\color{magenta}{●}\,\)の値です。

四分位数で区切られるのは値ではなく度数です。
例えば前後の\(\,7\,\)番目、\(\,9\,\)番目の値も同じ可能性はありますが、
中央値となる\(\,\color{red}{8}\,\)番目の値は\(\,57\,\)回です。
ア
最小値は\(\,35\,\)回ですが\(\,2\,\)番目の値も\(\,35\,\)回かもしれません。×
イ
最大値は間違いなく\(\,95\,\)回です。○
ウ
平均値は箱ひげ図からは読み取ることはできません。×
（\(\,57\,\)回は中央値です。）
※
平均値を表すときは「＋」を箱ひげ図の中に印すことはあります。
『覚え太郎』－「箱ひげ図」で確認しておいて下さい。
エ
６回以下の人は少なくとも\(\,8\,\)人はいますが、
\(\,9\,\)人目は\(\,61\,\)回以上でも同じ箱ひげ図になります。×
例　\(○○○●○○○\,,\,\color{red}{57}\,,\,62\,,\,62\,,\,○●○○○\)
オ
第３四分位数が\(\,60\,\)より大きいので少なくとも\(\,4\,\)人はいます。○

答え　\(\,\underline{　イ\,,\,オ　}\,\)

第２問関数の基本性質の確認

\(\,\large{2}\,\)
関数の性質なので簡単にグラフを書いて考えると良いです。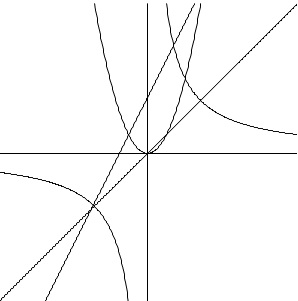定数は定まっていませんが、
\(\,a\,,\,b\,\)が\(\,0\,\)でなければ一般的にいえるはずです。
(1)
「変化の割合」は比例と１次関数は一定です。
　\(\hspace{4pt}\displaystyle （\,変化の割合\,）=\frac{　(\,y\,の増加量\,)　}{　(\,x\,の増加量\,)　}\)
①
　\(\hspace{10pt}y=ax+b\)\(\,\underline{　○　}\,\)
②
　\(\hspace{10pt}y=ax^2\)\(\,\underline{　×　}\,\)
グラフ上の２点の取り方で変化の割合は違います。

(2)
今度は関数から特徴を考えます。
「すべて」選ぶので順に見ていきましょう。
ア
１次関数は\(\,y\,\)軸対称ではありません。×
イ
\(\,y\,\)軸と交点を持たないのは反比例だけです。○
ウ
\(\,x=1\,\)をそれぞれの関数に代入してみれば分かります。
\(\,b\,\)が\(\,0\,\)でないので\(\,y=ax+b\,\)は\(\,y=a\,\)ではありません。×
エ
みる範囲は\(\,y\,\)軸より右です。
\(\,a＞0\,\)のとき（上のグラフはすべて\(\,a＞0\,\)です。）
反比例のグラフだけは\(\,x\,\)が増加（右に移動）すると\(\,y\,\)は減少します。○

答え　\(\,\underline{　イ\,,\,エ　}\,\)

おおよそ一般的に成り立つことを聞いてくれているので直感的でも良いですが、
グラフを描いて考えることを問題は求めていると思います。

第３問規則性とその利用

\(\,\large{3}\,\)
簡単な規則性と連立方程式です。
　\(a\,,\,5\,,\,b\,,\,|\,\,a\,,\,5\,,\,b\,,\,|\,a\,,\,5\,,\,b\,,\,|\,a\,,\,5\,,\,\cdots \)

\(\,(\,a\,,\,5\,,\,b\,)\,\)の３つの数の繰り返しになっています。
(1)
　\(\hspace{10pt}20=3\times 6+2\)
なので\(\,(\,a\,,\,5\,,\,b\,)\,\)を\(\,6\,\)回繰り返したあとの二つ目の数です。

答え　\(\,\underline{　5　}\,\)

(2)
条件が２つあることと文字が２つなので連立方程式ですね。
７番目までの和は\(\hspace{4pt}7=3\times \color{red}{2}+1\)なので、
\(\,(\,a\,,\,5\,,\,b\,)\,\)２セットに\(\,a\,\)を加えることになります。
　\(\hspace{10pt}\color{red}{2}(a+5+b)+a\\
=3a+2b+10\)
これが\(\,18\,\)なので
　\(\hspace{10pt}3a+2b+10=18　･･･①\)

５０番目までの和は\(\hspace{4pt}50=3\times \color{blue}{16}+2\)なので
\(\,(\,a\,,\,5\,,\,b\,)\,\)１６セットに\(\,a+5\,\)を加えることになります。
　\(\hspace{10pt}\color{blue}{16}(a+5+b)+a+5\\
=17a+16b+85\)
これが\(\,121\,\)なので
　\(\hspace{10pt}17a+16b+85=121　･･･②\)

\(\,①\,,\,②\,\)から連立方程式を解いて
　\(\hspace{10pt}\underline{　a=4\,,\,b=-2　}\)

連立方程式の処理はたくさん練習していいると思うので省略します。

⇒　加減法とは？連立方程式の解き方とポイント

ここでは代入法より加減法ですね。
代入法の場合は\(\,①\,\)から\(\,\color{blue}{2b}=\color{red}{8-3a}\,\)を\(\,②\,\)に代入すると良いです。
　\(\begin{eqnarray}
17a+16b&=&36\\
17a+8(\,\color{blue}{2b}\,)&=&36\\
17a+8(\color{red}{8-3a})&=&36\\
17a+64-24a&=&36\\
-7a&=&-28\\
a&=&4
\end{eqnarray}\)

普通に加減法で良いと思います。

第４問平面図形（平行四辺形）と作図

\(\,\large{4}\,\)
平面図形（平行四辺形）の問題で合同と反例です。
(1)
合同の証明です。

⇒　中学の図形証明問題(合同･相似)の解き方と証明の書き方ポイント

証明はルールに外れていなければどうでも良いので、
好きなようにまとめて下さい。

「平行四辺形」とあれば定義と定理の４つは必ず思い出しておきましょう。
平行四辺形になる条件は５つあるので確認も忘れずに。

(2)
逆の反例を示す作図です。

「反例」とは〔ことがら〕（命題）が必ず正しいとはいえない１つの例のことです。
ここでは(1)の〔ことがら〕の逆の反例です。

確かに(1)の場合は四角形は平行四辺形になります。
ですが合同になる三角形は回転だけではなく、
対称移動でもできるので
　\(\hspace{4pt}\mathrm{AB=CB}\)
　\(\hspace{4pt}\mathrm{DA=DC}\)
の場合も\(\,\mathrm{BD}\,\)を共通とする合同な三角形ができるのでそれが反例になります。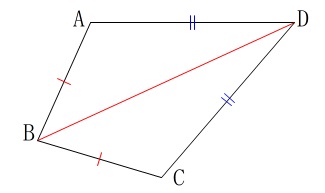作図は対称移動なので点\(\,\mathrm{A}\,\)から\(\,\mathrm{BD}\,\)に垂線を引いても良いのですが、
円２つで済むのでそちらを解答例にしておきます。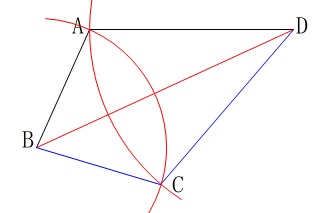垂線を引く場合も手順が増えるだけで間違いではありませんよ。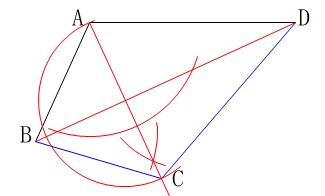作図はできるだけシンプルに、
というのはありますけど気にしないでおきましょう。

第５問時間と移動距離の関係を表す関数

\(\,\large{5}\,\)
関数の問題ですが\(\,\large{2}\,\)とは違い具体的な利用になります。

図\(\,\mathrm{Ⅰ}\,\)、\(\,\mathrm{Ⅱ}\,\)の絵とグラフ\(\,\mathrm{Ⅲ}\,\)があります。
絵で状況を理解できたら与えられた関数とグラフから考えれば良いです。

状況を簡単に説明すると、
電車が\(\,\mathrm{P}\,\)地点を加速しながら出発します。
出発してからの時間\(\,x\,\)と移動距離\(\,y\,\)との関係は
　\(\hspace{4pt}\displaystyle y=\frac{1}{4}\,x^2\)
電車が出発するとき、少し後ろから一定の速さで一也さんが同じ方向に移動しています。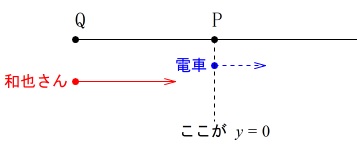後は問題に合わせて関数とグラフ利用で進めましょう。
(1)
出発してから\(\,6\,\)秒後、つまり\(\,x=6\,\)のときの移動距離\(\,y\,\)です。
　\(\begin{eqnarray}\displaystyle
y&=&\frac{1}{4}\times (\,6\,)^2\\
&=&\underline{　9　}\,(\,\mathrm{m}\,)
\end{eqnarray}\)

(2)
状況は先に説明した通りです。
①
グラフの\(\,y\,\)座標は\(\,\mathrm{P}\,\)地点からの距離を示しています。
グラフが上にある部分は移動距離が大きいので前にいることになります。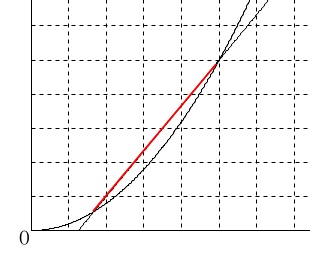答え　\(\,\underline{　イ　}\,\)

②
地点\(\,\mathrm{Q}\,\)は電車が出発するときの和也さんの位置です。
グラフでいうと和也さんの移動を表す関数の\(\,y\,\)切片を求めれば良いということです。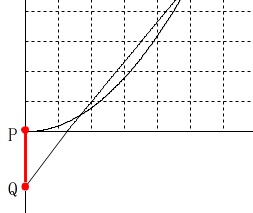つまり問題は和也さんの移動を表す関数を求める事になるので１次関数を求めましょう。

和也さんの速さは\(\,\displaystyle \frac{10}{3}\,\)なので、
　\(\hspace{4pt}\displaystyle y=\frac{10}{3}\,x+b\)
とおけます。
電車が出発して\(\,10\,\)秒後に同じ地点にいたので、
電車の移動距離を表す関数から
　\(\begin{eqnarray}\displaystyle
y&=&\frac{1}{4}\times (10)^2\\
&=&25
\end{eqnarray}\)
つまり\(\,\,(\,10\,,\,25\,)\,\)が交点の１つなので
　\(\begin{eqnarray}
25&=&\frac{10}{3}\times (10)+b\\
75&=&100+3b\\
b&=&-\frac{25}{3}
\end{eqnarray}\)
この絶対値は点\(\,\mathrm{Q}\,\)から点\(\,\mathrm{P}\,\)までの距離を意味します。

答え　\(\displaystyle \underline{\underline{　\frac{25}{3}　}}\,(\,\mathrm{m}\,)\)

１次関数は傾きと、通る１点があれば求まります。

⇒　1次関数の交点の座標とグラフから直線の方程式を求める方法

傾きも切片も求めることになるので、
２点を通る１次関数は短時間で求められるほど練習はしておいた方が良いです。

③
和也さんが\(\,\mathrm{P}\,\)（\(\,\,y=0\,\,\)）を通るのは\(\,②\,\)の関数から
　\(\begin{eqnarray}
0&=&\frac{10}{3}\,x-\frac{25}{3}\\
10x&=&25\\
x&=&\frac{25}{10}=\frac{5}{2}\,(\,秒後\,)
\end{eqnarray}\)

このとき電車は
　\(\hspace{4pt}\displaystyle y=\frac{1}{4}\times \left(\,\frac{5}{2}\,\right)^2 =\frac{25}{16}\,(\,\mathrm{m}\,)\)
移動しています。

答え　\(\displaystyle \underline{\underline{　\frac{25}{16}　}}\,(\,\mathrm{m}\,)\)

距離なので２つの関数の差を考えますが、
　\(\hspace{4pt}\displaystyle \frac{1}{4}\,x^2-\left(\frac{10}{3}\,x-\frac{25}{3}\right)\)
地点\(\,\mathrm{P}\,\)を\(\,y=0\,\)としているので和也さんの移動距離は考えなくても求まります。
ただし、和也さんが地点\(\,\mathrm{P}\,\)を通る時間\(\,x\,\)は求めなくてはなりません。

第６問平面図形（円の性質と部分面積）

\(\,\large{6}\,\)
平面図形ですがややこしそうな円があります。
こういうときは問題の順に条件を整理していきましょう。
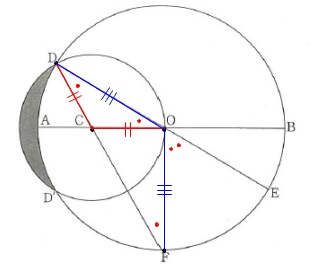分かり易いところを示していきました。

(1)
円の半径は常に一定なので二等辺三角形ができます。
底角が等しくなる事と円周角の定理から説明できます。

図から読み取れることから説明の中をうめていきます。

線分\(\,\mathrm{OF}\,\)を補助することがポイントですが問題で示してくれているので大丈夫でしょう。

(2)
長さと角度の条件が加わります。
　\(\hspace{10pt}\mathrm{AB}=12\,,\,∠\mathrm{BOF}=90°\)
※長さの単位は\(\,\mathrm{cm}\,\)ですが省略します。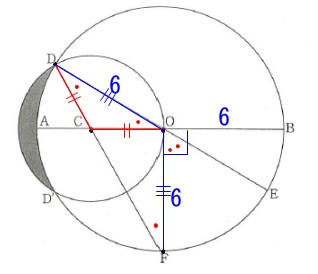線分\(\,\mathrm{AB}\,\)は直径なので半径が\(\,\color{blue}{6}\,\)であることで示しています。
①
対頂角は等しいので\(\,\mathrm{∠BOE=∠AOD}\,\)となります。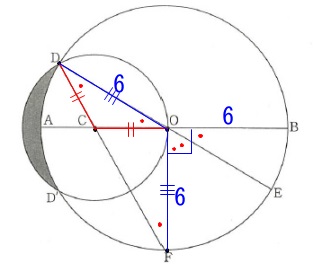(1)で説明しているので分かるでしょう。
\(\,\mathrm{∠BOE}\,\)は\(\,\mathrm{∠BOF=90°}\,\)を三等分しています。
　\(\hspace{4pt}\mathrm{∠BOE=∠AOD=∠CFO=\color{red}{∠EDF}}=\underline{　30°　}\)
②
①の角度が分かったところで三角定規と正三角形が見えてきますが、
先ずは\(\,\mathrm{CO}\,\)を求めておきましょう。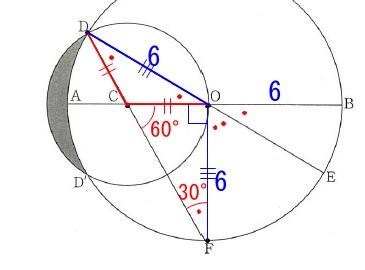\(\,\mathrm{△COF}\,\)は三角定規になるので
　\(\begin{eqnarray}\displaystyle
\mathrm{CO:FO}&=&1:\sqrt{3}\\
\mathrm{CO}:6&=&1:\sqrt{3}\\
\sqrt{3}\,\mathrm{CO}&=&6\\
\mathrm{CO}&=&\frac{6}{\sqrt{3}}=\underline{　2\sqrt{3}　}(\,\mathrm{cm}\,)
\end{eqnarray}\)
ここまではそれ程方針は変わらないでしょう。

③
下弦の月のような部分面積です。
これは方針が分かれると思いますので色々試してみて下さい。

ここでは中心\(\,\mathrm{C}\,\)、半径\(\,\mathrm{CO}\,\)の円から部分的に引いていきます。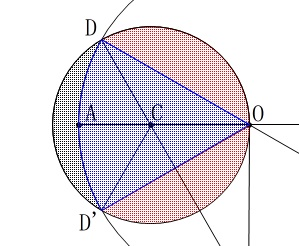青の部分のおうぎ形と赤い部分の面積を引きます。

流れとしては順序が違いますが必要な長さがあるので求めておきます。
②で求めている長さが円の半径で
　\(\hspace{10pt}\mathrm{CO}=\color{red}{2\sqrt{3}}\)
点\(\,\mathrm{C}\,\)から\(\,\mathrm{OD}\,\)に垂線を下ろしてできる下図の\(\,\mathrm{△OCT}\,\)は三角定規なので
　\(\hspace{10pt}\mathrm{CT}=\color{blue}{\sqrt{3}}\)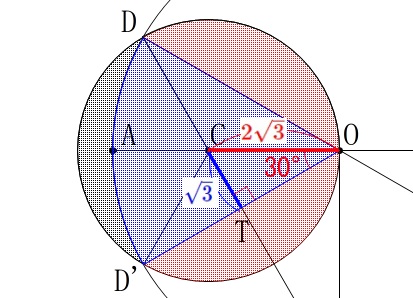これは赤い部分の面積を求める際に必要になると気が付くでしょう。

では面積を計算していきましょう。
点\(\,\mathrm{C}\,\)中心で半径\(\,\mathrm{CO}\,\)の円の面積\(\,\color{red}{S_1}\,\)は
　\(\hspace{10pt}\color{red}{S_1}=\pi\,(\,2\sqrt{3}\,)^2=\color{red}{12\,\pi}\)
青い部分は半径\(\,\color{blue}{6}\,\)で中心角が\(\,60°\,\)のおうぎ形です。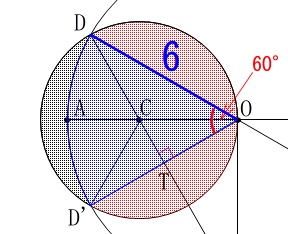青い部分の面積を\(\,\color{blue}{S_2}\,\)とすると
　\(\begin{eqnarray}\displaystyle
\color{blue}{S_2}&=&\pi\,(\,6\,)^2\times \frac{60}{360}\\
&=&\color{blue}{6\,\pi}
\end{eqnarray}\)
赤い部分の面積は半径\(\,\mathrm{CO}\,\)中心角\(\,\mathrm{120°}\,\)のおうぎ形から、
底辺\(\,\color{blue}{6}\,\)高さ\(\,\color{blue}{\sqrt{3}}\,\)の三角形を引きます。
（三角形は\(\,\mathrm{△COD\,,\,△COD’}\,\)どちらで考えても同じです。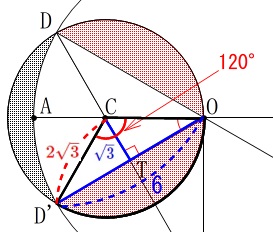）赤い部分の面積の１つを\(\,\color{magenta}{S_3}\,\)とすると
　\(\begin{eqnarray}
\color{magenta}{S_3}&=&\pi\,\,(\color{red}{2\sqrt{3}}\,)^2\times \frac{120}{360}-\frac{1}{2}\times \color{blue}{6}\times \color{blue}{\sqrt{3}}\\
&=&\color{magenta}{4\,\pi-3\sqrt{3}}
\end{eqnarray}\)
赤い部分は2つあるので求める面積\(\,S\,\)は
　\(\begin{eqnarray}
S&=&\color{red}{S_1}-\color{blue}{S_2}-2\color{magenta}{S_3}\\
&=&\color{red}{12\,\pi}-\color{blue}{6\,\pi}-2(\color{magenta}{4\,\pi-3\sqrt{3}})\\
&=&12\,\pi-6\,\pi-8\,\pi+6\sqrt{3}\\
&=&\underline{　6\sqrt{3}-2\,\pi　}\,(\,\mathrm{cm^2}\,)
\end{eqnarray}\)

点\(\,\mathrm{C}\,\)は円の中心で\(\,\mathrm{△CDD’}\,\)が二等辺三角形となるので、
\(\,\mathrm{△ODD’}\,\)が正三角形です。
（\(\,\mathrm{∠DCO=∠120°}\,\)なので円周角が正三角形の１角で\(\,60°\,\)。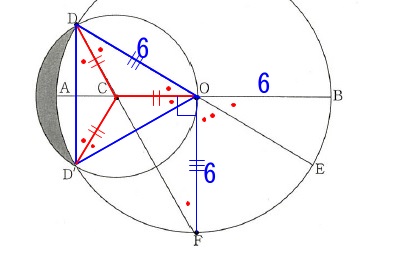）これを利用しても同じような方法で答えにたどり着けると思います。

一気に答えにたどり着ける公式があるとは限りません。
一歩一歩分かることをつなげて、
答えまでたどり着こうとするかどうかを問いかける問題ですね。

以上です。
さらっと済ませてしまいましたので間違いがあればご指摘下さい。

⇒　群馬県公立高校入試の数学の過去問題と解答解説

基礎的な内容は前期選抜の解説で詳しくしてあります。
ここで対策を細かくするつもりはありませんが、
前期を制限時間の半分くらいで終わらせるくらい基礎を徹底することが対策になります。

クラブ活動で忙しい！
塾に通っているのに数学が苦手！
数学の勉強時間を減らしたい！
数学の勉強方法が分からない！

その悩み、『覚え太郎』が解決します！！！