2023年(令和5年)度福岡県公立高校入試の数学の問題と解説

２０２３年(令和５年)度福岡県公立高校入試の数学の問題と解説です。
第１問の小問集合から第６問の空間図形問題まで良い問題がそろっています。
テンションが下がる第３問以外はシンプルなので一気に進めますが、
解答用紙への留意点などありますので受験生はあらかじめ知っておくと良いです。

2023年(令和5年)度福岡県公立高校入試の数学の問題

令和５年度の数学の問題です。

⇒　2023年(令和5年)度福岡県公立高校入試の数学の問題ＰＤＦ

解答用紙への留意点が問題用紙の２ページにありますので確認しておきましょう。

2023年(令和5年)度福岡県公立高校入試の数学の解説

６０点満点で１問の配点は見た目より大きいのでミスには気をつけておきたいですね。

第１問

\(\large{\color{black}{\fbox{1}}}\)
(1)
　\(\hspace{10pt}9+4\times (-3)\\
=9-12\\
=\underline{　-3　}\)

計算順序と符号にすれば問題ないでしょう。

(2)
　\(\hspace{10pt}2(5a+4b)-(a-6b)\\
=10a+8b-a+6b\\
=\underline{　9a+14b　}\)

時間が欲しいという気持ちは分からないでもないですが、
暗算は極力避けて２行目を入れた方が結果として早いです。

(3)
　\(\hspace{10pt}\displaystyle \frac{18}{\sqrt{3}}-\sqrt{27}\\
\displaystyle =\frac{18\sqrt{3}}{3}-3\sqrt{3}\\
\displaystyle =6\sqrt{3}-3\sqrt{3}\\
=\underline{　3\sqrt{3}　}\)

分母の有理化と素因数分解を省略していますが、
無理数計算に自信のない人は必ずやっておきましょう。

(4)
２次方程式を解きます。

　\(\begin{eqnarray}
(x-5)(x+4)&=&3x-8\\
x^2-x-20&=&3x-8\\
x^2-4x-12&=&0\\
(x+2)(x-6)&=&0\\
x&=&\underline{　-2\,,\,6　}
\end{eqnarray}\)

２次「方程式を解く」ことと「解を求める」ことは同じことですよ。
左辺が因数分解されていて気持ちよく解ける方法がありそうですが、
展開して左辺にすべての項を集めて処理する基本通りで良いです。

(5)
さいころ２つの出目の積が偶数になる確率です。

樹形図でも表でも良いです。
整数の積が偶数になるより奇数になる方が少ないので、
積が奇数になる方を見ていきます。
　\(\begin{array}{|c|c|c|c|c|c|c|} \hline
& 1 & \,2\, & 3 & \,4\, & 5 & \,6\,\\ \hline
\,1\, & × & & × & & × & \\ \hline
2 & & 　 & & 　 & & 　\\ \hline
3 & × & & × & & × & \\ \hline
4 & & & & & & \\ \hline
5 & × & & × & & × & \\ \hline
6 & & & & & & \\ \hline
\end{array}\)

３６通り中１２通りが奇数になるので、
積が偶数になるのは２４通りなので確率は
　\(\hspace{10pt}\displaystyle \frac{24}{36}=\underline{\underline{　\frac{3}{4}　}}\)

余事象を考えて確率を出したなら
　\(\hspace{10pt}\displaystyle 1-\frac{1}{4}=\frac{3}{4}\)
としたと思いますがどっちでも良いです。

ここで確認しておいて欲しいのは（大したことではないですが）
奇数と偶数の積は
　\(（\color{red}{奇数}）\times （\color{red}{奇数}）=（\color{red}{奇数}）\)
　\(（\color{red}{奇数}）\times （\color{blue}{偶数}）=（\color{blue}{偶数}）\)
　\(（\color{blue}{偶数}）\times （\color{red}{奇数}）=（\color{blue}{偶数}）\)
　\(（\color{blue}{偶数}）\times （\color{blue}{偶数}）=（\color{blue}{偶数}）\)
ということです。

(6)
１次関数における\(\,y\,\)の増加量を求めます。
　\(\hspace{10pt}y=-2x+7\)
　\(\hspace{4pt}x:-1 \rightarrow 4\)

変化の割合（傾き）を利用しようが２点から求めようがどっちでも良いです。
２点から求めると
　\(\hspace{4pt}(\,-1\,,\,\color{blue}{9}\,)\)
　\(\hspace{4pt}(\,4\,,\,\color{red}{-1}\,)\)
\(\,y\,\)の増加量は\(\,9\,\)から\(\,-1\,\)まで変化したので
　\(\hspace{10pt}\color{red}{-1}-(\color{blue}{9})=\underline{　-10　}\)
減っているのは分かるので符号の間違いも起こりにくいでしょう。

傾きを利用すると
　\(\hspace{10pt}(\,y\,の増加量\,)=(\,傾き\,)\times (\,x\,の増加量\,)\)
なので\(\,x\,\)の増加量が\(\,5\,\)だから
　\(\hspace{10pt}\displaystyle -2\times 5\,=\,-10\)
でも良いです。

変化の割合は
　\(\hspace{10pt}\displaystyle (\,変化の割合\,)=\frac{　(\,y\,の増加量\,)　}{　(\,x\,の増加量\,)　}\)

この形が基本なのでどっちでも良いですが、
２点を書き出すという作業は何より優先しておくと良いです。

(7)
関数のグラフを書きます。
　\(\hspace{10pt}\displaystyle y=-\frac{4}{x}\)

反比例ですが比例定数が負なのでグラフの位置に注意しますが、
グラフを書くときの基本通り点をとっていくことで間違えはしないでしょう。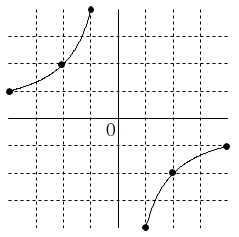

(8)
標本調査なので比例式でおおよその数値を推定します。

求める人数をおおよそ\(\,x\,\)人とすると
　\(\begin{eqnarray}
450:x&=&40:32\\
40x&=&450\times 32\\
x&=&\underline{　360　}
\end{eqnarray}\)

(9)
角度を求めます。
条件から分かる角度をどんどん書き込んで行きましょう。

条件（問題文から分かること）
　・線分\(\,\mathrm{AB}\,\)は直径
　・\(\,\mathrm{AC}\,\)∥\(\,\mathrm{OE}\,\)
　・\(\,\mathrm{∠CAB=56°}\,\)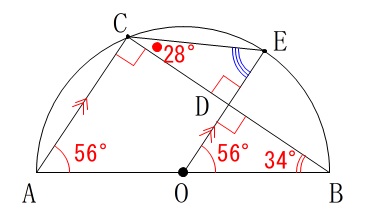直径に対する円周角、平行線の同位角から
　\(\hspace{10pt}\mathrm{∠ACB=∠ODB}=90°\)
　\(\hspace{10pt}\mathrm{∠CAB=∠EOB}=56°\)
また中心角\(\,\mathrm{∠EOB}\,\)に対する円周角から
　\(\hspace{10pt}\mathrm{∠BCE}=28°\)
となるので三角形の内角の和から
　\(\begin{eqnarray}
\mathrm{∠DEC+∠DCE}+90°&=&180°\\
\mathrm{∠DEC}+28°&=&90°\\
\mathrm{∠DEC}&=&\underline{　62°　}
\end{eqnarray}\)

もちろん
　\(\begin{eqnarray}
\mathrm{∠DCE+∠DEC}&=&\mathrm{∠ODC}\\
28°＋\mathrm{∠DEC}&=&90°\\
\mathrm{∠DEC}&=&\underline{　62°　}
\end{eqnarray}\)
でも良いですよ。

※
「\(\,\mathrm{∠CBA=34°}\,\)は使わないじゃないか」と思うかもしれませんが、
実際問題を解く時点では分かる角度を書き出していくので、
その過程をそのまま図にしておきました。
きれいな解答を求めるなら自分で解くときに消せば良いです。
（消すことの方が無駄に思えますけど。）

他にも単純に考えれば遠回りかもしれませんが、
\(\,\mathrm{∠AOD}\,\)を出しておいて四角形\(\,\mathrm{AOEC}\,\)の内角からでもでます。

方法は１つではないと言うことがわかってくれればそれでいいです。

第２問

\(\large{\color{black}{\fbox{2}}}\)
比例計算と方程式です。
(1)
\(\,20\,\)％引きだと定価の\(\,80\,\)％になるので
定価（\(\,100\,\)％）を\(\,x\,\)として比例式で出しておくと
　\(\begin{eqnarray}
100:x&=&80:a\\
80x&=&100\,a\\
x&=&\frac{100}{80}\,a\\
&=&\underline{\underline{　\frac{5}{4}\,a　}}
\end{eqnarray}\)

当会お勧めの比例計算に慣れている人なら
　\(\hspace{10pt}\displaystyle a\times \frac{100}{80}=\underline{\underline{　\frac{5}{4}\,a　}}\)
と時計回りの計算で瞬時に答えが出ていたでしょう。

⇒　比例式の応用 文章題への利用と便利な比の使い方

当会で紹介してからずいぶん日が経ちますので、
同じ方法で説明してくれるところも最近は増えてきていると思います。

(2)
あめは足りるかどうかの説明ですが、
方程式を解く必要があります。

そのためにあめの個数を\(\,x\,\)とするか、
生徒の人数を\(\,x\,\)とするかどちらかで方程式を立てます。

ポイントは方程式を立てるとき変わっていないものを「＝」で結ぶということです。

①
あめの個数を\(\,x\,\)とすると、
変わっていないのは人数です。
（あめの個数も変わっていませんけど。）

「あめを６個ずつ分けると８個余り」
ということから８個引いておけば人数で割り切れるので
　\(\hspace{10pt}\displaystyle \frac{x-8}{5}\)
これが生徒の人数です。
「あめを７個ずつ分けると１０個たりない」
ということから１０個足しておけば人数で割り切れるので
　\(\hspace{10pt}\displaystyle \frac{x+10}{7}\)
これも生徒の人数です。

生徒の人数は等しいので
　\(\begin{eqnarray}
\frac{x-8}{5}&=&\frac{x+10}{7}\\
7(x-8)&=&5(x+10)\\
7x-56&=&5x+50\\
2x&=&106\\
x&=&\color{red}{53}　(個)
\end{eqnarray}\)
このとき生徒の人数は
　\(\hspace{10pt}\displaystyle \frac{\color{red}{53}-8}{5}=\frac{\color{red}{53}+10}{7}=\color{blue}{9}\)
よって、６個ずつ配るとすると
　\(\hspace{10pt}\displaystyle 6\times \color{blue}{9}=54　(個)\)
必要なので「\(\,\underline{　足りない。　}\,\)」が答えです。

②
生徒の人数を\(\,x\,\)とすると、
あめの個数は変わらないので
　\(\begin{eqnarray}
5x+8&=&7x-10\\
x&=&\color{blue}{9}　(人)
\end{eqnarray}\)
このときあめの個数は
　\(\hspace{10pt}\displaystyle 5\times 9+8=7\times 9-10=\color{red}{53}　(個)\)

よって、６個ずつ配ると
　\(\hspace{10pt}\displaystyle 6\times 9=54　(個)\)
必要なので「足りない。」が答えです。

どちらでも良いですが、個人的には②が先でした。
（見直しで①もやってみましたが分数よりは、先に②です。）
※
「じゃあ、解説も②を先にやれよ。」、という突っ込みはいりません。
どちらも整数だけど人数の方が少ないはず、
だから人数を\(\,x\,\)とする方が楽？だからじゃないですかね。
（人ごとみたいだけど。）

第３問

\(\large{\color{black}{\fbox{3}}}\)
箱ひげ図の読み取りです。

なぜテンションが下がるかというと、
国語の問題？って程に日本語が多いからです。
（第４問もそうですが意図があり、わざとだと思います。）

３つ全部を読みとっても時間がかかるだけなので、
問題に合わせて進めて行きます。

ちなみに箱ひげ図から元のデータを完全に復元することはできない、
とさらっと考えていけば良いです。

(1)
データ\(\,\mathrm{A}\,\)の範囲と四分位範囲を答えます。

データ\(\,\mathrm{A}\,\)の四分位数を見ておきましょう。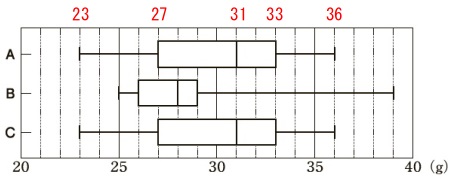「範囲」は最大値から最小値を引けば良いので、
　\(\hspace{10pt}\displaystyle 36-23=\underline{　13　}\)

「四分位範囲」は第３四分位数から第１四分位数をひけば良いので
　\(\hspace{10pt}\displaystyle 33-27=\underline{　6　}\)

ここは用語の確認なので意味はしっかり覚えておきましょう。

(2)
箱ひげ図からいえることの根拠を読み取ります。
「３０\(\,\mathrm{g}\,\)以上の個数は、\(\,\mathrm{A}\,\)が１５個以上、\(\,\mathrm{B}\,\)が７個以下」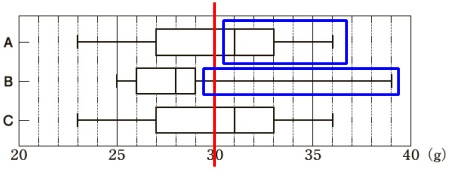\(\,\mathrm{A}\,\)の箱ひげ図から中央値（第２四分位数）が\(\,31\,\)なので、
\(\,30\,\mathrm{g}\,\)以上の個数は少なくとも\(\,15\,\)個以上はあります。

全体の個数は\(\,30\,\)個なので中央値\(\,31\,\)以上は少なくとも半分の\(\,15\,\)はあります。
データの個数が偶数なので中央値となる\(\,31\,\)はないかもしれませんが、
少なくとも半分以上は\(\,30\,\mathrm{g}\,\)以上だとはいえます。

答え　\(\,\underline{　ウ　中央値　\,,\,　31　\mathrm{g}　}\,\)

\(\,\mathrm{B}\,\)の箱ひげ図の第３四分位数\(\,29\,\)は上から\(\,8\,\)番目のデータを含みます。
\(\,29\,\mathrm{g}\,\)が何個あっても第３四分位数は\(\,29\,\)になりますが、
\(\,\mathrm{30\,g}\,\)以上の個数は多くても\(\,7\,\)個以下です。

答え　\(\,\underline{　オ　第３四分位数　\,,\,　29　\mathrm{g}　}\,\)

データの個数が偶数なので中央値が本当にあるのかはわかりませんが、
第１四分位数と第３四分位数は同じ値のデータが複数合っても存在します。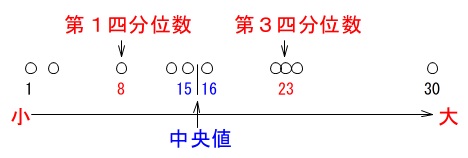この場合だと中央値は小さい順に並べたとき１５番目と１６番目の平均値になります。
（同じ値であっても平均値は同じ。）
第１四分位数は８番目で、第３四分位数は２３番目ですが、
同じ値が何個あっても変わりません。

(3)
箱ひげ図とヒストグラムの比較です。

箱ひげ図からヒストグラムはかけませんが、
分布はおおよそ比較できます。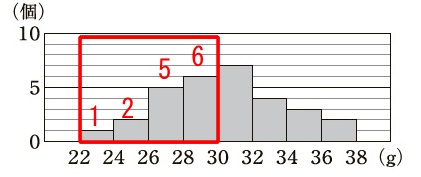先ずは\(\,\mathrm{A}\,\)のデータにおける累積度数です。
　\(\hspace{10pt}\underline{　14　}\)

⇒　度数分布表とは？階級の幅と階級値および累積度数とヒストグラム

用語の確認なので足し算を間違えないようにして下さい。

次に\(\,\mathrm{C}\,\)のデータをヒストグラムにするとどれか選びます。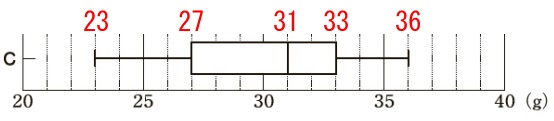各四分位数は確認しておいて下さい。

１つだけが適合するらしいので不適なものを削除していきましょう。

順番に見ていっても良いですが、
明らかに分かるものから削除していけば時間の節約にはなりますね。
ここでは順番に説明しておきます。

アのヒストグラム。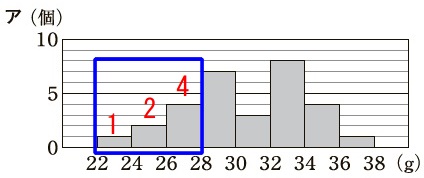第１四分位数が\(\,27\,\mathrm{g}\,\)なので、
\(\,28\,\mathrm{g}\,\)未満の累積度数は\(\,8\,\)以上のはずです。×
（データは全部で\(\,30\,\)個だというのは忘れないように。）
※
度数\(\,8\,\)という数字の意味は(1)(2)を見直しておいて下さい。

イのヒストグラム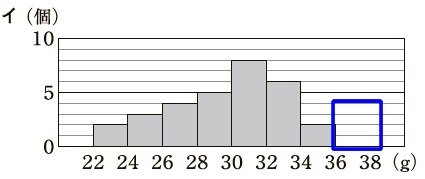箱ひげ図から最大値は\(\,36\,\mathrm{g}\,\)だから、
\(\,36\,\mathrm{g}\,\)以上\(\,38\,\mathrm{g}\,\)未満の階級の度数\(\,0\,\)はおかしい。×
（これはすぐに除外できたと思います。）

ウのヒストグラム。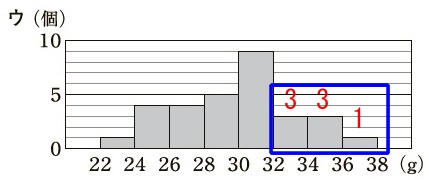第３四分位数は\(\,33\,\)なので、
\(\,\mathrm{32\,g}\,\)以上の度数は\(\,8\,\)なくてはおかしい。×

答え　\(\underline{　エ　}\)

細かくはわかりませんがエにおかしなところはありません。

箱ひげ図は度数で詳しく比較できませんが、
おおよその分布を見ることができます。

で、「重いいちご」とは？

第４問

\(\large{\color{black}{\fbox{4}}}\)
関数です。

時間が\(\,x\,\)で、道のりが\(\,y\,\)になることを意識していれば、
難しくはないのでさくっと終わらせましょう。

バスと自転車とタクシーが出てきます。
バスは出発してからの加速（速さが増す）を考えますが、
自転車とタクシーは一定の速さになってからなので考えなくて良いです。

位置関係については問題で確認しておいて下さい。

とりあえず\(\,\mathrm{P}\,\)地点からのバスと自転車の移動を表す関数を表しておきます。バス：\(\hspace{4pt}\displaystyle y=\frac{1}{4}\,x^2\,\)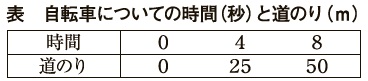自転車：\(\hspace{4pt}\displaystyle y=\frac{25}{4}\,x\)
これらが書かれた関数のグラフが図です。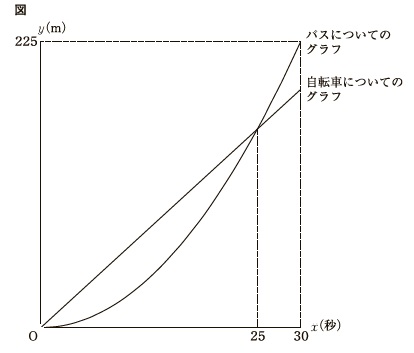この図が考え方の元になるので利用します。　

(1)
傾きの表す意味です。
　\(\hspace{10pt}\displaystyle (傾き)=\frac{　(\,y\,の増加量\,)　}{　(\,x\,の増加量\,)　}\)

変化の割合のことですが\(\,x\,,\,y\,\)の意味を考えると
　\(\hspace{10pt}\displaystyle \frac{　(\,道のり\,)　}{　(\,時間\,)　}=\underline{\underline{　(\,\color{red}{速さ}\,)　}}\)
であることは分かります。

\(\,x\,\)の変化は\(\,0\,\rightarrow \,6\,\)なので、
\(\,6\,\)秒後までの平均の速さです。

バスは加速するので速さが時間とともに変化します。
だから２点を結んだ直線の傾きは「平均の速さ」を表すことになります。

答え　\(\,\underline{　ウ　}\,\)

(2)
関数から\(\,\mathrm{P}\,\)地点から\(\,\mathrm{100\,m}\,\)東までのバスと自転車の時間を求めれば良いです。
ただし、求めるものを間違えないようにしましょう。

\(\,\mathrm{P}\,\)地点を出発してからの時間を考えます。
バス：
　\(\begin{eqnarray}
\frac{1}{4}\,x^2&=&100\\
x^2&=&400\\
x&=&\color{red}{20}\,(\,x\,＞\,0\,)
\end{eqnarray}\)
バスは\(\,20\,\)秒後に\(\,\mathrm{Q}\,\)を通過します。

自転車：
　\(\begin{eqnarray}
\frac{25}{4}\,x&=&100\\
25x&=&400\\
x&=&\color{blue}{16}
\end{eqnarray}\)
自転車は\(\,16\,\)秒後に\(\,\mathrm{Q}\,\)を通過します。

よって、自転車が\(\,\mathrm{Q}\,\)を通過した後バスは
　\(\hspace{10pt}20-16=\underline{　4　}\,(秒後)\)
に\(\,\mathrm{Q}\,\)を通過します。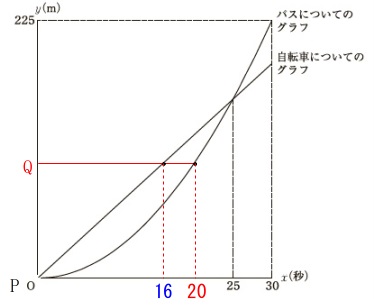地点\(\,\mathrm{Q}\,\)では自転車の方が先を行っていることは確認できました。
（問題に「\(\,25\,\)秒後に追いつく」とあります。）

(3)
タクシーの速さは秒速\(\,\mathrm{10\,m}\,\)です。

バスが出発して\(\,10\,\)秒後に\(\,\mathrm{P}\,\)地点を通過するということは。
タクシーは
　\(\hspace{10pt}10\times 10=100\,\mathrm{m}\)
\(\,\mathrm{P}\,\)地点より西にいたということになります。
このことからタクシーを表す関数は
　\(\hspace{10pt}y=10\,x-100\)

このことからタクシーが自転車に追いつくのは
　\(\begin{eqnarray}
\frac{25}{4}\,x&=&10\,x-100\\
25\,x&=&10\,x-400\\
15\,x&=&400\\
x&=&\frac{400}{15}=\underline{\underline{　\frac{80}{3}　}}\,(\,秒後\,)
\end{eqnarray}\)

バスが自転車に追いつくのは\(\,25\,\)秒なので
　\(\hspace{10pt}\displaystyle 25=\frac{75}{3}\)
だから
　\(\hspace{10pt}\displaystyle \frac{80}{3}\,＞\,\frac{75}{3}=25\)

よって、\(\,25\,\)より\(\,\underline{　大きい　}\,\)（時間がよりかかる）ので、
バスより先に追いつくことは\(\,\underline{　できない　}\,\)。

それぞれの関数を表すことができれば基本問題です。
数の大小比較は数の世界を統一、って会員にはいうまでもありませんね。

先に進みます。

第５問

\(\large{\color{black}{\fbox{5}}}\)
平面図形の問題です。

合同と相似の証明があります。
条件を追いかけていけば良いようにまとまっているので、
問題の順に進めて行きましょう。

(1)
正方形の周上の点に条件がついていいます。
　\(\hspace{10pt}\mathrm{BE=CF}\)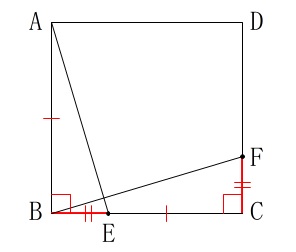
これは問題全体に通じる条件です。

証明は図の中で証明を終わらせておきましょう。
すでに示しているので合同条件を書くだけです。

答え　\(\,\underline{　２組の辺とその間の角　}\,\)がそれぞれ等しい。

合同な図形の対応する辺は等しいので、
　\(\hspace{10pt}\mathrm{AE=BF}\)
がいえます。
このことをいうための合同の証明です。

(2)
点は(1)と異なるとは書いてありますが条件は変わっていないので、
証明に必要な合同条件は同じです。

答え　\(\,\underline{　イ　}\,\)

(3)
相似の証明です。
　\(\,\mathrm{△ABE}\,\)∽\(\,\mathrm{△AGB}\,\)

これも図の中で証明を終わらせましょう。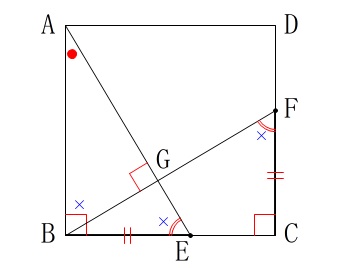合同であることは分かっています。
　\(\,\mathrm{△ABE}\,\)≡\(\,\mathrm{△BCF}\,\)
このことから
　\(\hspace{10pt}\mathrm{\color{blue}{∠AEB=∠BFC}}\)
正方形の対辺は平行なので錯角が等しく
　\(\hspace{10pt}\mathrm{\color{blue}{∠BFC=∠ABG}}\)
つまり
　\(\hspace{10pt}\mathrm{\color{blue}{∠AEB=∠ABG}}　･･･①\)
共通の角なので
　\(\hspace{10pt}\mathrm{\color{red}{∠BAE=∠GAB}}　･･･②\)
\(\,①\,②\,\)より２組の角がそれぞれ等しい。
よって、
　\(\,\mathrm{△ABE}\,\)∽\(\,\mathrm{△AGB}\,\)

気がついていると思いますが相似な三角形は他にもありますね。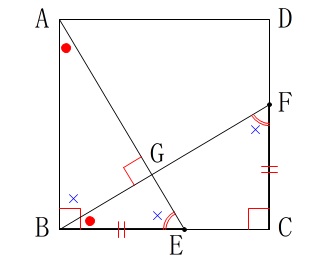これを踏まえて(4)を考えましょう。

(4)
ようやく長さが登場です。
といっても比だけで具体的な長さではないので、
適当に長さを設定しても答えは出せるはずです。
　\(\hspace{10pt}\mathrm{BE:EC}=3:1\)
このとき四角形\(\,\mathrm{GECF}\,\)の面積が正方形\(\,\mathrm{ABCD}\,\)の何倍かを求めます。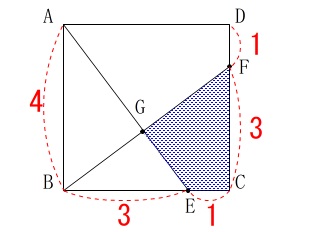与えられたのは比ですが正方形の１辺を\(\,\color{red}{4}\,\)としておきます。

相似がたくさんあるのですべての長さ（の比）がでますが、
辺\(\,\mathrm{BG\,,\,GE}\,\)が分かれば\(\,\mathrm{△AEG}\,\)の面積からなんとかなりそうです。
（\(\,\mathrm{BG}\,\)だけでも答えは出ます。）

あれやこれやと説明してもややこしくなるので、
三平方の定理で簡単に説明しておきます。

確認ですが
　\(\,\mathrm{△ABE}\,\)≡\(\,\mathrm{△BCF}\,\)
　\(\,\mathrm{△ABE}\,\)∽\(\,\mathrm{△AGB}\,\)∽\(\,\mathrm{△BGE}\,\)
で、すべて直角三角形です。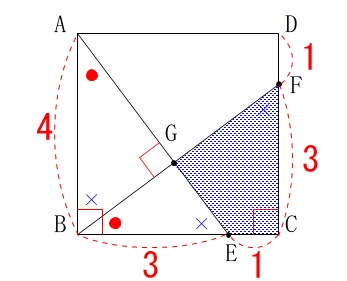\(\,\mathrm{△ABE}\,\)に三平方の定理を用いて
　\(\begin{eqnarray}
\mathrm{AE^2}&=&\mathrm{AB^2+BE^2}\\
\mathrm{AE^2}&=&4^2+3^2\\
&=&25\\
\mathrm{AE}&=&\pm 5
\end{eqnarray}\)
長さなので
　\(\hspace{10pt}\mathrm{AE}=\color{blue}{5}\)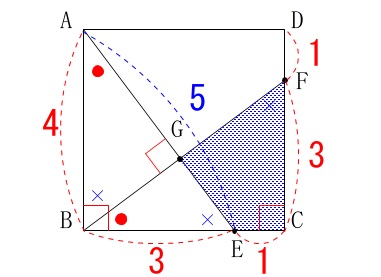また合同な三角形でもあるので
　\(\hspace{10pt}\mathrm{AE=BF}=\color{blue}{5}\)
（これはなくても答えは出ます。）

直角三角形なので底辺と高さを求めて行けば良いですね。
　\(\,\mathrm{△ABE}\,\)∽\(\,\mathrm{△BGE}\,\)
だから
　\(\begin{eqnarray}
\mathrm{AB:AE}&=&\mathrm{BG:BE}\\
4:5&=&\mathrm{BG}:3\\
\mathrm{BG}&=&\color{magenta}{\frac{12}{5}}
\end{eqnarray}\)
また
　\(\begin{eqnarray}
\mathrm{BE:AE}&=&\mathrm{GE:BE}\\
3:5&=&\mathrm{GE}:3\\
\mathrm{GE}&=&\color{magenta}{\frac{9}{5}}
\end{eqnarray}\)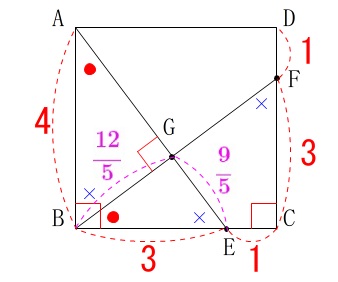これから
　\(\begin{eqnarray}
\mathrm{△BGE}&=&\frac{1}{2}\times \mathrm{GE}\times \mathrm{BG}\\
&=&\frac{1}{2}\times \color{magenta}{\frac{12}{5}}\times \color{magenta}{\frac{9}{5}}\\
&=&\frac{54}{25}
\end{eqnarray}\)
直角三角形\(\,\mathrm{BCF}\,\)の面積は
　\(\hspace{4pt}\displaystyle \frac{1}{2}\times 3\times 4=6\)
なので四角形\(\,\mathrm{GECF}\,\)の面積\(\,S\,\)は
　\(\begin{eqnarray}
S&=&6-\frac{54}{25}\\
&=&\frac{150-54}{25}\\
&=&\color{blue}{\frac{96}{25}}
\end{eqnarray}\)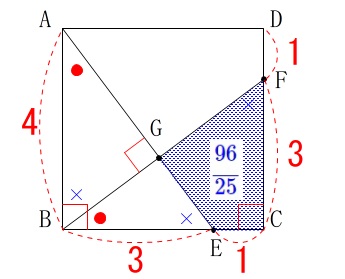よって、正方形の面積は\(\,\color{red}{16}\,\)なので
　\(\hspace{10pt}\displaystyle \frac{96}{25}\div 16 =\underline{\underline{　\frac{6}{25}　}}\,(\,倍\,)\)
※
この割り算の順序がわかりにくい人は簡単な整数で考えてみてください。
\(\,\color{blue}{5}\,\)は\(\,\color{red}{1}\,\)の何倍か？
　\(\hspace{10pt}\color{blue}{5}\div \color{red}{1}\,=\,5\,(倍)\)
とするように、
\(\,\color{blue}{a}\,\)は\(\,\color{red}{b}\,\)の何倍か？
　\(\hspace{10pt}\displaystyle \color{blue}{a}\div \color{red}{b}=\frac{a}{b}\,(倍)\)
と「\(\,a\,\)は」を「\(\,b\,\)の」で割れば良いです。
「四角形\(\,\mathrm{GECF}\,\)は」「正方形\(\,\mathrm{ABCD}\,\)の」何倍か？
　\(\hspace{10pt}\displaystyle \frac{96}{25}\div 16=\frac{6}{25}\,(倍)\)

\(\,\mathrm{△BGE}\,\)の面積は辺の比で進めた人も割といたでしょう。
　\(\hspace{10pt}\displaystyle \mathrm{GF}=5-\frac{12}{5}=\color{magenta}{\frac{13}{5}}\)
なので
　\(\hspace{4pt}\mathrm{BG:GF}=12:13\)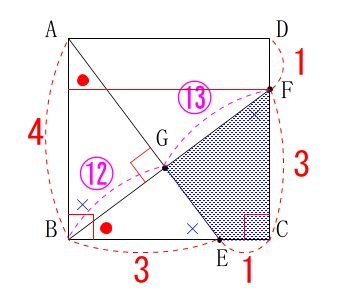\(\,\mathrm{△BCF}\,\)の面積が\(\,6\,\)なので、
　\(\begin{eqnarray}
\mathrm{△BGE}&=&\mathrm{△BCF}\times \frac{12}{12+13}\times \frac{3}{1+3}\\
&=&6\times \frac{12}{25}\times \frac{3}{4}\\
&=&\frac{54}{25}
\end{eqnarray}\)
どっちでも良いですよ。

※（この先の一部は見なくて良いです。\(\color{black}{\fbox{5}}\)に進んでください。）
正方形\(\,\mathrm{ABCD}\,\)から比だけで進めると
\(\,\mathrm{△BCF}\,\)の面積が正方形\(\,\mathrm{ABCD}\,\)の
　\(\hspace{4pt}\displaystyle \frac{1}{2}\times 4\times 3\div 16=\frac{3}{8}\,(\,倍\,)\)
なので（上の図の赤線で切った長方形に注目）
　\(\hspace{10pt}\displaystyle \frac{3}{8}\times \left\{\color{red}{1}-\frac{12}{12+13}\times \frac{3}{1+3}\right\}\\
\displaystyle =\frac{3}{8}\times \frac{16}{25}=\frac{6}{25}\,(\,倍\,)\)
（\(\,\mathrm{△BCF}\,\)の比を\(\,\mathrm{△BGE}\,\)との比で\(\,\color{red}{1}\,\)とみています。）
何をやっているかわかる人は『超え太郎』をお守りにしているレベルの人ですね。
詳しい説明は不要でしょう。すみません、先に進みます。

第６問

\(\large{\color{black}{\fbox{6}}}\)
空間図形です。

空間図形は平面図形が基本になりますが序盤は立体特有の性質です。

与えられる立体は、
「半径\(\,\color{red}{4}\,\)の円を底面とし、母線の長さが\(\,\color{blue}{6}\,\)」
の円すいです。※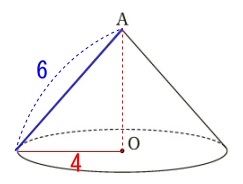
長さの単位は\(\,\mathrm{cm}\,\)ですが省略します。

母線って何だっけ？という状態の人は『覚え太郎』を徹底的にやってください。
数学が苦手なのではなく、準備不足なだけです。
何で今まで数学で苦労してたのか自分で不思議に思うくらい変われるはずです。

(1)
円すいの「表面積」です。

展開図のおうぎ形の中心角は適当で良いですよ。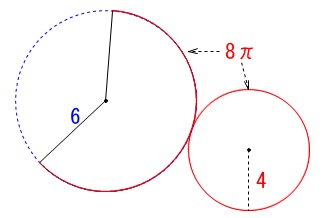面積計算は今では普通に出回っていると思うので、
説明も必要無いくらいでしょう。

⇒　円錐(すい)の表面積や四角錐,五角錐の体積の求め方

おうぎ形の面積は円を基本に比例計算で良いですが、
公式を使って手早く求めておきましょう。
　\(\hspace{10pt}\displaystyle \frac{1}{2}\times 8\,\pi\times 6=\color{magenta}{24\,\pi}\)
底面の円の面積は半径が\(\,4\,\)なので\(\,\color{blue}{16\,\pi}\,\)。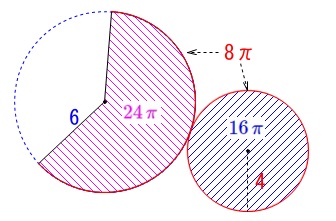よって求める表明積を\(\,S\,\)とすると
　\(\begin{eqnarray}
S&=&\color{magenta}{24\,\pi}+\color{blue}{16\,\pi}\\
&=&\underline{　40\,\pi　}\,(\,\mathrm{cm^2}\,)
\end{eqnarray}\)

おうぎ形の部分の面積を比例計算する場合、
円周が\(\,\color{blue}{12\,\pi}\,\)に対して弧の長さが\(\,\color{red}{8\,\pi}\,\)なので、
中心角を求めなくても良いですよ。
　\(\hspace{10pt}\displaystyle \pi\,(6)^2\times \frac{8\,\pi}{12\,\pi}\\
\displaystyle =36\,\pi\times \frac{2}{3}\\
=24\,\pi\)

弧（円周）が\(\,12\,\pi\,\)のとき円の面積が\(\,36\,\pi\,\)で、
弧が\(\,8\,\pi\,\)のときおうぎ形の面積は？という比例計算です。

(2)
円すいの体積が円柱の何倍か、です。

これは円すいだけでなくて三角すいでも四角すいでもすべて同じで、
（底面の形に関係なく）
　\(\displaystyle (\,すい体の体積\,)=\color{red}{\frac{1}{3}}\times (\,柱体の体積\,)\)
となります。

つまり高さが同じ容器に入れると高さは\(\displaystyle \,\frac{1}{3}\,\)になるということです。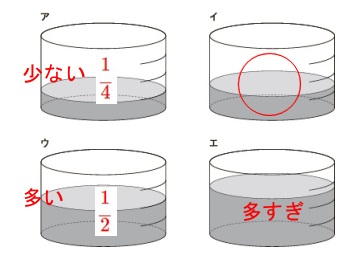答え　\(\,\underline{　イ　}\,\)

底から水面までの高さは円すいの高さの\(\displaystyle \,\frac{1}{3}\,\)なので、
円すいの高さを三平方の定理で求めれば良いですね。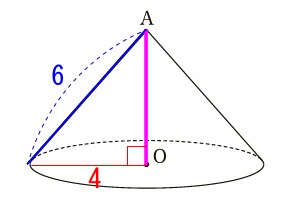円すいの高さは長さなので正で、
　\(\begin{eqnarray}
\mathrm{OA^2}+4^2&=&6^2\\
\mathrm{OA^2}&=&20\\
\mathrm{OA}&=&2\sqrt{5}\,(\,＞\,0\,)
\end{eqnarray}\)

よって求める水面までの高さは
　\(\hspace{10pt}\displaystyle \frac{1}{3}\times 2\sqrt{5}=\underline{\underline{　\frac{2\sqrt{5}}{3}　}}(\,\mathrm{cm}\,)\)

(3)
立体の中にある線分の長さを求めます。

条件は問(1)(2)にあるものに
　\(\hspace{10pt}\displaystyle \mathrm{∠BOC}=120°\)
　\(\hspace{10pt}\mathrm{AC=DC}\)
が加わります。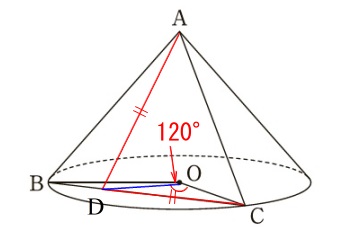このときの線分\(\,\mathrm{OD}\,\)を求めます。

立体のままではとらえにくいので、
いつものように平面を抜き出して考えましょう。

抜き出すのは\(\,\mathrm{△ABC\,,\,△OBC\,,\,△ADO}\,\)の３つです。
やってみれば必要な部分が見えてくるのでどこからみていくかは好きにして良いです。
ここでは問題に書かれている条件の順に進めましょう。

　\(\hspace{10pt}\displaystyle \mathrm{∠BOC}=120°\)
この条件から\(\,\mathrm{△OBC}\,\)を抜き出すと、
辺\(\,\mathrm{BC}\,\)の長さが分かります。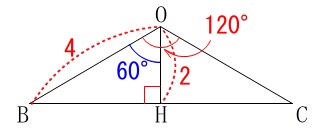点\(\,\mathrm{O}\,\)から\(\,\mathrm{BC}\,\)に垂線を下ろして交点を\(\,\mathrm{H}\,\)とすると、
\(\,\mathrm{△OBH}\,\)は三角定規なので\(\,\mathrm{BH}\,\)、と\(\,\mathrm{BC}\,\)の長さが分かります。
　\(\hspace{10pt}\mathrm{BH}=\color{blue}{2\sqrt{3}}\,,\,\mathrm{BC}=4\sqrt{3}\)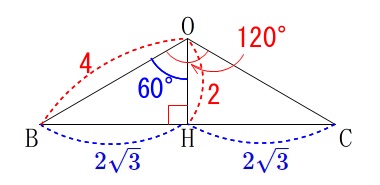次の条件は
　\(\hspace{10pt}\mathrm{AC=DC}\)
になるので\(\,\mathrm{△ABC}\,\)を抜き出すと相似な三角形が見えてきます。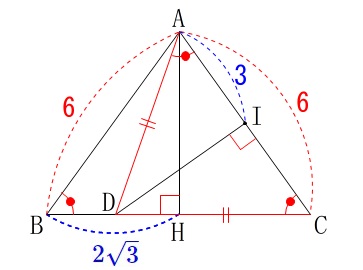二等辺三角形が２つあって底角が等しいから、
　\(\,\mathrm{△ABC}\,\)∽\(\,\mathrm{△DCA}\,\)
また点\(\,\mathrm{D}\,\)から\(\,\mathrm{AC}\,\)に垂線を引いて\(\,\mathrm{AC}\,\)との交点を\(\,\mathrm{I}\,\)とすると、
　\(\,\mathrm{△ABH}\,\)∽\(\,\mathrm{△DAI}\,\)
となるので
　\(\begin{eqnarray}
\mathrm{AB:BH}&=&\mathrm{DA:AI}\\
\color{red}{6}:\color{blue}{2\sqrt{3}}&=&\mathrm{DA}:\color{blue}{3}\\
2\sqrt{3}\times \mathrm{DA}&=&6\times 3\\
\mathrm{DA}&=&\frac{6\times 3}{2\sqrt{3}}\\
&=&\color{magenta}{3\sqrt{3}}
\end{eqnarray}\)

円すいの高さは
　\(\hspace{10pt}\displaystyle \mathrm{OA}=2\sqrt{5}\)
なので三平方の定理を利用して\(\,\mathrm{OD}\,\)の長さが求まります。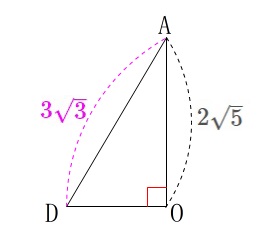　\(\begin{eqnarray}
\mathrm{OD^2+AO^2}&=&\mathrm{AD^2}\\
\mathrm{OD^2}+(2\sqrt{5})^2&=&(\color{magenta}{3\sqrt{3}})^2\\
\mathrm{OD^2}+20&=&27\\
\mathrm{OD^2}&=&7\\
\mathrm{OD}&=&\pm \sqrt{7}
\end{eqnarray}\)
長さだから
　\(\hspace{10pt}\displaystyle \mathrm{OD}=\underline{　\sqrt{7}　}(\,\mathrm{cm}\,)\)

これは一気に方向性が見えているわけではなく、
角度を求めるときと同じで分かる長さから求めているだけです。

\(\,\mathrm{△ABC}\,\)の中での情報を処理する段階がポイントかもしれませんね。

条件は何を伝えてくれているのか見ていくと良いです。
問題に不要な条件はないのですよ。
※
場合によっては使わなくても良い条件はたまにありますが、
それは『超え太郎』クラスの上の知識がある場合です。

以上です。
※
入力ミス等に気がついたときはご連絡頂けると幸いです。

⇒　福岡県公立高校入試数学過去問の解答解説

解いて見て毎年思うことですが、
福岡県の公立入試の数学は重っ苦しい難問ではありません。
数学に必要な基本知識と数学問題を解くときに必要な作業を、
上手く組み合わせた良い問題です。

偏りも少ないので他県の受験生も入試対策の仕上げに利用すると良いです。