2023年(令和5年)度滋賀県公立高校入試の数学の問題と解説

2023年(令和5年)度滋賀県公立高校入試の数学の問題と解説です。
大問は４つと少なく見えますがボリュームは十分。
問題の出され方はシンプルなので取り組みやすく見えて、実は差がつきやすいです。
滋賀県にしては作図が比較的楽な分、他の図形問題に比重が置かれている印象です。

2023年（令和5年）度滋賀県公立高校入試の数学の問題

令和５年度の数学の問題です。

⇒　2023年（令和5年）度滋賀県公立高校入試の数学の問題ＰＤＦ

\(\color{black}{\fbox{1}}\)から\(\color{black}{\fbox{4}}\)までの大問４つ。
解答用紙も問題の最後にあるので参考にして下さい。

2023年（令和5年）度滋賀県公立高校入試の数学の解説

全体を通じて計算力を試すようなややこしい数値計算はないですが、
数学の基礎をしっかりおさえておかないと時間が足りないと感じるかもしれません。

第１問小問集合

\(\large{\color{black}{\fbox{1}}}\)
シンプルな基礎確認問題です。
(1)
　\(\hspace{10pt}13+3\times (-2)\\
=13-6\\
=\underline{　7　}\)

掛け算が先です。
(2)
　\(\hspace{10pt}\displaystyle \frac{1}{3}\,a-\frac{5}{4}\,a\\
\displaystyle =\frac{4a-15a}{12}\\
\displaystyle =\underline{\underline{　-\frac{11}{12}\,a　}}\)

通分して分子の計算に集中ですね。
符号の（\(\,-\,\)）や\(\,a\,\)は分子にあっても良いです。
(3)
等式の変形です。
　\(\begin{eqnarray}
3x+7y&=&21\\
3x&=&21-7y\\
x&=&\underline{\underline{　\frac{21-7y}{3}　}}
\end{eqnarray}\)

項を分けて
\(\hspace{10pt}\displaystyle x=7-\frac{7}{3}\,y\)
でも良いですよ。
（\(\,y\,\)の項が先でも良いです。）
(4)
連立方程式を解きます。
どの二組でも同じですが定数を利用しましょう。
　\( \begin{cases}
\hspace{4pt} 2x+y=-1　･･･①\\
\hspace{4pt} 5x+3y=-1　･･･②
\end{cases}\)
\(\,①\,\)の両辺を３倍して一文字\(\,y\,\)を消去します。
\(\hspace{14pt}6x+3y=-3\\
\underline{-)\,5x+3y=-1　}\\
\hspace{18pt}x\hspace{23pt}=-2\)
\(\,①\,\)に戻して（\(\,②\,\)でも同じです。）
　\(\begin{eqnarray}
2(-2)+y&=&-1\\
y&=&3
\end{eqnarray}\)
答え\(\hspace{10pt}\underline{　x=-2\,,\,y=3　}\)
(5)
無理数計算です。
　\(\hspace{10pt}\displaystyle \frac{9}{\sqrt{3}}-\sqrt{12}\\
\displaystyle =\frac{9\sqrt{3}}{3}-2\sqrt{3}\\
=3\sqrt{3}-2\sqrt{3}\\
=\underline{　\sqrt{3}　}\)

分母の有理化と素因数分解を無理数計算で確認するのは、
都道府県によらず定番です。
暗算は避けて確実に取りましょう。
(6)
因数分解です。
　\(\hspace{10pt}x^2-2x-24\\
=\underline{　(x+4)(x-6)　}\)

定数項に着目して
\(\hspace{4pt}1\times 24\,,\,2\times 12\,,\,3\times 8\,,\,4\times 6\)
の中から１次の係数あわせです。
(7)
回転体の体積です。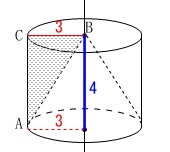円柱から円すいを引けば良いだけですが、
円すいの体積は円柱の\(\,\displaystyle \frac{1}{3}\,\)になることから、
求める体積は円柱の\(\,\displaystyle \frac{2}{3}\,\)です。
　\(\hspace{10pt}\displaystyle \pi\,(\,3\,)^2\times 4\times \frac{2}{3}\\
\displaystyle =\underline{　24\,\pi　}\)
円柱の体積は
\(\hspace{10pt}\displaystyle \pi\,(\,3\,)^2\times 4=36\,\pi\)
円すいの体積は
\(\hspace{10pt}\displaystyle \frac{1}{3}\times \pi\,(\,3\,)^2\times 4=12\,\pi\)
なので
\(\hspace{10pt}36\,\pi-12\,\pi=24\,\pi\)
の計算をまとめてやっただけです。

⇒　表面積や体積の求め方(三角柱,四角柱,円柱,球や半球)

公式として覚えておかないと体積は求められないものが多いです。
(8)
四分位数を求める問題です。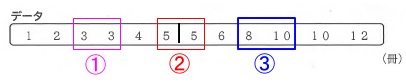第３四分位数はデータの右半分６個の中央値です。
答え\(\hspace{10pt}\underline{　9　}(点)\)

⇒　代表値とは？度数分布表の平均値,中央値の求め方と最頻値の答え方

中央値って何？とならないように小学校で学んだ代表値は忘れないように。
(9)
確率です。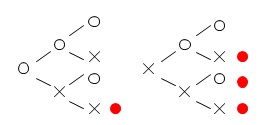あれこれ考えるより樹形図が一番早いです。
３枚の硬貨なので出方は８通りで、そのうち４通りが裏が２枚以上。

答え\(\hspace{10pt}\displaystyle \frac{4}{8}=\underline{\underline{　\frac{1}{2}　}}\)

「２枚以上が裏」なので３枚とも裏もありますよ。

第２問作図と図形総合

\(\large{\color{black}{\fbox{2}}}\)
線分、面積、立体とあります。
(1)
正三角形の作図です。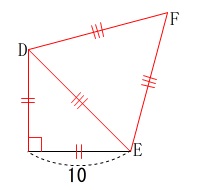１辺１０の直角二等辺三角形を描いて、
斜辺\(\,10\sqrt{2}\,\)を１辺とする正三角形を描けばできあがりです。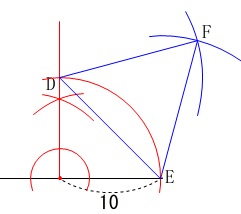線分を延長することも作図の手順の１つです。

この問題の場合は単に正三角形を描くのではないので、
解答には記号\(\,\mathrm{D,E,F}\,\)も入れておくことを忘れないように。
(2)
弧の長さを求めますが、展開図だけで解決します。
底面の円の直径が\(\,\color{red}{5}\,\)なので、
弧\(\,\mathrm{BB’}\,\)の長さは\(\,\color{red}{5\,\pi}\,\)です。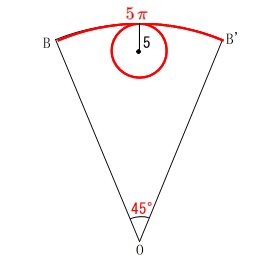中心角が\(\,45°\,\)らしいので、
半径\(\,\mathrm{OB}\,\)を\(\,\color{blue}{r}\,\)とすると
　\(\begin{eqnarray}
2\,\pi\,\color{blue}{r}\times \frac{45}{360}&=&5\,\pi\\
\color{blue}{r}&=&\color{blue}{20}
\end{eqnarray}\)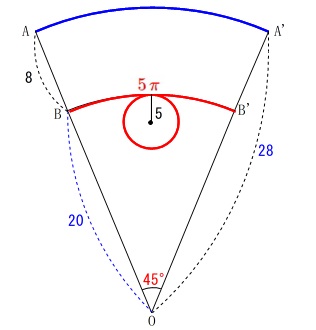弧\(\,\mathrm{AA’}\,\)の長さは半径\(\,\color{blue}{28}\,\)、中心角\(\,45°\,\)なので
　\(\begin{eqnarray}
(弧\mathrm{AA’})&=&2\,\pi\,(28)\times \frac{45}{360}\\
&=&\underline{　7\,\pi　}\,(\,\mathrm{cm}\,)
\end{eqnarray}\)

比例式でも良いです。
　\(\begin{eqnarray}
(弧\mathrm{BB’}):(弧\mathrm{AA’})&=&\mathrm{OB:OA}\\
5\,\pi:(弧\mathrm{AA’})&=&20:28\\
20\times (弧\mathrm{AA’})&=&5\,\pi\times 28\\
(弧\mathrm{AA’})&=&7\,\pi\,(\,\mathrm{cm}\,)
\end{eqnarray}\)

図を書けるスペースを空けてくれていることがありがたいです。
(3)
切り取る正方形の長さを求めます。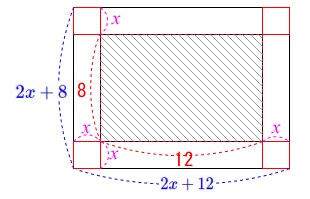切り取る正方形の１辺を\(\,x\,\)とすると、
元の長方形は、
縦の長さが\(\,\color{blue}{2x+8}\,\)、横の長さは\(\,\color{blue}{2x+12}\,\)になり、
中の斜線部分の長方形の面積の２倍だから
　\(\begin{eqnarray}
(2x+8)(2x+12)&=&2\times 8\times 12\\
2(x+4)2(x+6)&=&2\times 8\times 12\\
(x+4)(x+6)&=&48\\
z^2+10x+24&=&48\\
x^2+10x-24&=&0\\
(x+12)(x-2)&=&0\\
x&=&-12\,,\,2
\end{eqnarray}\)
正方形の１辺の長さだから\(\,x\,＞\,0\,\)より
\(\hspace{10pt}x=\underline{　2　}(\,\mathrm{cm}\,)\)

図７は、容器の形を表しただけで平面図形問題です。
(4)
長さが与えられるので体積でも求めるのかと思いましたが、
ねじれの位置にある辺を答えるだけでした。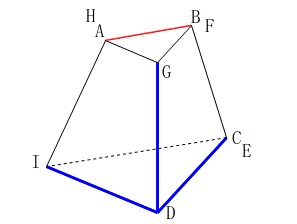\(\,\mathrm{△DCI}\,\)を底面と見て展開図を組み立てると、
重なる点が分かり易いです。
答え\(\hspace{4pt}\underline{　辺\,\mathrm{DG}\,,\,辺\,\mathrm{DE}\,(\,\mathrm{DC}\,)\,,\,辺\,\mathrm{DI}　}\,\)

⇒　空間図形の位置関係問題(平行,ねじれの位置,垂直な面,平行な面)

辺\(\,\mathrm{AI}\,\)とねじれの位置にある辺だと少し違った説明が必要になっていました。

第３問関数

\(\large{\color{black}{\fbox{3}}}\)
原点を頂点とする２次関数について考えます。
条件を整理しておきましょう。
\(\hspace{10pt}\displaystyle y=2\,x^2　･･･①\)
\(\hspace{10pt}\displaystyle y=-\,x^2　･･･②\)
点\(\,\mathrm{P}\,\)は\(\,x\,\)軸上の点だから\(\,t\,＞\,0\,\)として
点\(\,\mathrm{P}\,(\,t\,,\,0\,)\,\)
点\(\,\mathrm{P}\,\)と\(\,x\,\)座標が同じになるので
\(\hspace{10pt}\mathrm{A}\,(\,t\,,\,2\,t^2\,)\,,\,\mathrm{B}\,(\,t\,,\,-\,t^2\,)\)
点\(\,\mathrm{C}\,\)は\(\,y\,\)軸について点\(\,\mathrm{A}\,\)と対称なので
\(\hspace{10pt}\mathrm{C}\,(\,-\,t\,,\,2\,t^2\,)\)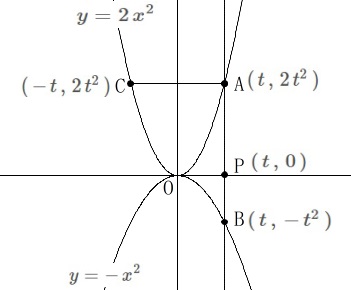(1)(2)は問題の条件を見ていなくても求まります。
(1)
関数\(\,y=-\,x^2\,\)について変化の割合を求めます。
\(\hspace{10pt}(\,1\,,\,-1\,)\)
\(\hspace{10pt}(\,3\,,\,-9\,)\)
なので変化の割合は
　\(\begin{eqnarray}
(変化の割合)&=&\frac{　(\,y\,の増加量\,)　}{　(\,x\,の増加量\,)　}\\
&=&\frac{-9-(-1)}{3-1}\\
&=&\underline{　-4　}
\end{eqnarray}\)
(2)
関数\(\,y=a\,x^2\,\)の比例定数を求めます。
点\(\,(\,2\,,\,2\,)\,\)を通るとき代入して成り立つから
　\(\begin{eqnarray}
2&=&a\times (\,2\,)^2\\
a&=&\underline{\underline{　\frac{1}{2}　}}
\end{eqnarray}\)
(3)
座標は\(\,t\,\)で表せています。
\(\hspace{10pt}\mathrm{A}\,(\,t\,,\,2\,t^2\,)\,,\,\mathrm{B}\,(\,t\,,\,-\,t^2\,)\)
\(\hspace{10pt}\mathrm{C}\,(\,-\,t\,,\,2\,t^2\,)\)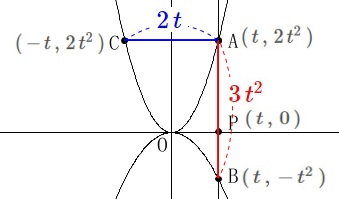
線分\(\,\mathrm{AB}\,\)は\(\,y\,\)座標の差なので
\(\hspace{4pt}\mathrm{AB}=2\,t^2-(\,-t^2\,)=\color{red}{3\,t^2}\)
線分\(\,\mathrm{AC}\,\)は\(\,x\,\)座標の差なので
\(\hspace{4pt}\mathrm{AC}=t-(\,-t\,)=\color{blue}{2\,t}\)
この２つの線分の和が\(\,\color{magenta}{1}\,\)なので
　\(\begin{eqnarray}
\mathrm{AB+AC}&=&1\\
\color{red}{3\,t^2}+\color{blue}{2\,t}&=&\color{magenta}{1}\\
3\,t^2+2\,t-1&=&0
\end{eqnarray}\)

ここからは解答時間の差が出ます。
　\(\begin{eqnarray}
x&=&\frac{-2\pm \sqrt{2^2-4\cdot 3\cdot (-1)}}{2\times 3}\\
&=&\frac{-2\pm \sqrt{4+12}}{6}\\
&=&\frac{-2\pm \sqrt{16}}{6}\\
&=&\frac{-2\pm 4}{6}\\
&=&\frac{-2+4}{6}\,,\,\frac{-2-4}{6}\\
&=&\frac{1}{3}\,,\,-1
\end{eqnarray}\)
条件から\(\,t\,＞\,0\,\)なので
\(\hspace{10pt}\displaystyle t=\underline{\underline{　\frac{1}{3}　}}\)
※
ルートの中の「\(\,\cdot\,\)」は掛け算の意味です。

もう少し楽をするための努力をしてきた人は
　\(\begin{eqnarray}
x&=&\frac{-1\pm \sqrt{1^2-3\cdot (1)}}{3}\\
&=&\frac{-1\pm \sqrt{1+3}}{3}\\
&=&\frac{-1\pm 2}{3}\\
&=&\frac{-1+2}{3}\,,\,\frac{-1-2}{3}\\
&=&\frac{1}{3}\,,\,-1
\end{eqnarray}\)

⇒　２次方程式の解の公式二通りの求め方と便利な公式と文章題の解き方

高校進学後の予習をした人は
　\(\begin{eqnarray}
3\,t^2+2\,t-1&=&0\\
(\,3t-1\,)(\,t+1\,)&=&0\\
t&=&\frac{1}{3}\,,\,-1
\end{eqnarray}\)
としたでしょう。

どれでも良いです。
問題がシンプルなのでミスをしないことが一番大切です。
(4)
変域が同じになるように傾きと\(\,y\,\)切片を求めます。
定義域（\(\,x\,\)の変域）が\(\,-1\,≦\,x\,≦\,3\,\)のとき
関数\(\,y=2\,x^2\,\)の値域（\(\,y\,\)の変域）は
\(\hspace{10pt}0\,≦\,y\,≦\,18\)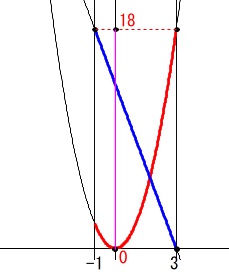傾き\(\,b\,\)が\(\,b\,＜\,0\,\)だから、
\(\,x\,\)が増加すると\(\,y\,\)は減少するので
\(\,x\,\)が\(\,-1\,\)のとき\(\,y\,\)が最大値\(\,18\,\)、（\(\,(\,-1\,,\,18\,)\,\)を通る。）
\(\,x\,\)が\(\,3\,\)のとき\(\,y\,\)が最小値\(\,0\,\)、（\(\,(\,3\,,\,0\,)\,\)を通る。）
を満たす直線の式を求めれば良い。
\(\hspace{10pt}\displaystyle y=-\frac{9}{2}+\frac{27}{2}\)
これから\(\,y=b\,x+c\,\)に係数を合わせて
\(\hspace{10pt}\displaystyle \underline{\underline{　b=-\frac{9}{2}\,,\,c=\frac{27}{2}　}}\)

この場合連立方程式を先に立てるかもしれません。
　\( \begin{cases}
\hspace{4pt} -b+c=18\\
\hspace{4pt} 3b+c=0
\end{cases}\)
係数を決めるだけなのでこちらでもそれ程変わりませんね。

第４問平面図形

\(\large{\color{black}{\fbox{4}}}\)
図形の証明と面積です。
(1)
角の二等分線定理の証明です。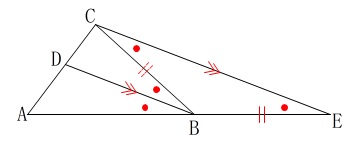本当なら補助線を引くことがこの証明のポイントになるのですが、
問題が補助線を引いてくれているので分かり易いでしょう。

\(\,\mathrm{∠B}\,\)の二等分線なので
\(\hspace{10pt}\mathrm{\color{red}{∠ABD}=\color{red}{∠CBD}}\)
平行線の同位角と錯角は等しくなるから
\(\hspace{10pt}\mathrm{\color{red}{∠CBD}=\color{blue}{∠BCE}}\)
\(\hspace{10pt}\mathrm{\color{red}{∠ABD}=\color{blue}{∠BEC}}\)
このことから
\(\hspace{10pt}\mathrm{\color{blue}{∠BCE}=\color{blue}{∠BEC}}\)
底角が等しいので\(\,\mathrm{△BCE}\,\)は二等辺三角形となり、
\(\hspace{10pt}\mathrm{BC=BE}\)
よって、\(\,\mathrm{△ABD}\,\)∽\(\,\mathrm{△AEC}\,\)なので
　\(\begin{eqnarray}
\mathrm{BA:BC}&=&\mathrm{BA:BE}\\
&=&\mathrm{AD:DC}
\end{eqnarray}\)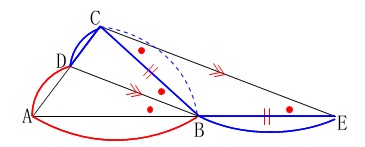証明より結果を利用したい定理です。
(2)
三角定規が見えます。
①
面積比です。
具体的な面積も出せるので、相似でもどちらでも良いですよ。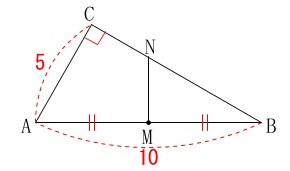\(\,\mathrm{△ABC}\,\)は三角定規なので、
\(\hspace{10pt}\mathrm{BC}=\color{blue}{5\sqrt{3}}\)
また、\(\,\mathrm{M}\,\)は\(\,\mathrm{AB}\,\)の中点で
\(\hspace{10pt}\mathrm{AM=BM}=\color{red}{5}\)
　\(\,\mathrm{△ABC}\,\)∽\(\,\mathrm{△NBM}\,\)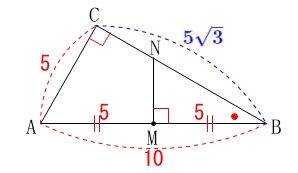具体的な面積で比を出すと相似比から
　\(\begin{eqnarray}
\mathrm{AC:BC}&=&\mathrm{NM:BM}\\
\color{red}{5}:\color{blue}{5\sqrt{3}}&=&\mathrm{NM}:\color{red}{5}\\
\mathrm{NM}&=&\frac{5\times 5}{5\sqrt{3}}\\
&=&\frac{5}{\sqrt{3}}=\color{magenta}{\frac{5\sqrt{3}}{3}}
\end{eqnarray}\)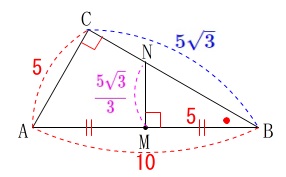　\(\begin{eqnarray}
\mathrm{△ABC:△NBM}&=&\left(\frac{1}{2}\times \color{red}{5}\times \color{blue}{5\sqrt{3}}\right):\left(\frac{1}{2}\times \color{magenta}{\frac{5\sqrt{3}}{3}}\times \color{red}{5}\right)\\
&=&1:\frac{1}{3}\\
&=&\underline{　3:1　}
\end{eqnarray}\)

相似比で済ますなら
相似比が
\(\hspace{10pt}\mathrm{BC:BM}=5\sqrt{3}:5=\sqrt{3}:1\)
なので面積比は
　\(\begin{eqnarray}
\mathrm{△ABC:△NBM}&=&(\,\sqrt{3}\,)^2:1^2\\
&=&\underline{　3:1　}
\end{eqnarray}\)

相似比利用の方が\(\,\mathrm{MN}\,\)を出さなくていいので早いです。
相似比が\(\,\color{red}{a}:\color{blue}{b}\,\)のとき、面積比は\(\,\color{red}{a^2}:\color{blue}{b^2}\,\)です。
②
長さの条件は①と同じですが、
おうぎ形と三角定規しか見えていません。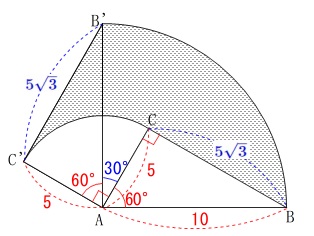おうぎ形\(\,\mathrm{ABB’}\,\)と直角三角形\(\,\mathrm{AB’C’}\,\)の面積の和から、
直角三角形\(\,\mathrm{ABC}\,\)とおうぎ形\(\,\mathrm{ACC’}\,\)を引きましょう。

一度にやると「ややこしく見える」ので部分的に求めて行きます。
　\(\begin{eqnarray}
(おうぎ形\mathrm{ABB’})&=&\pi\,(\,10\,)^2\times \frac{90}{360}\\
&=&\color{red}{25\,\pi}
\end{eqnarray}\)
　\(\begin{eqnarray}
\mathrm{△ABC}&=&\frac{1}{2}\times 5\times 5\sqrt{3}\\
&=&\color{red}{\frac{25\sqrt{3}}{2}}
\end{eqnarray}\)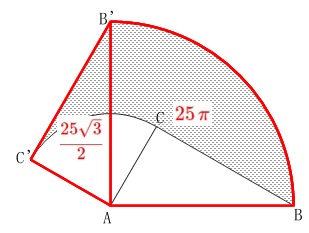白い部分の面積は、
　\(\begin{eqnarray}
\mathrm{△ABC}&=&\frac{1}{2}\times 5\times 5\sqrt{3}\\
&=&\color{blue}{\frac{25\sqrt{3}}{2}}
\end{eqnarray}\)
　\(\begin{eqnarray}
(おうぎ形\mathrm{ACC’})&=&\pi\,(\,5\,)^2\times \frac{90}{360}\\
&=&\color{blue}{\frac{25}{4}\,\pi}
\end{eqnarray}\)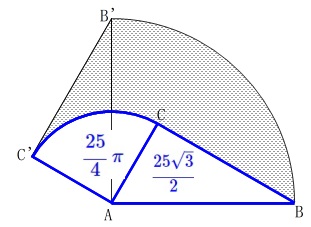
求める面積\(\,S\,\)は
　\(\begin{eqnarray}
S&=&\left(\,\color{red}{25\,\pi}+\color{red}{\frac{25\sqrt{3}}{2}}\,\right)-\left(\,\color{blue}{\frac{25\sqrt{3}}{2}}+\color{blue}{\frac{25}{4}\,\pi}\,\right)\\
&=&\color{red}{25\,\pi}-\color{blue}{\frac{25}{4}\,\pi}\\
&=&\underline{\underline{　\frac{75}{4}\,\pi　}}
\end{eqnarray}\)

「\(\,\mathrm{△ABC}\,\)は関係ない？」
と思う人は考えることが好きですね。
図形的な意味を見ていくと同じ面積を表す部分があるのです。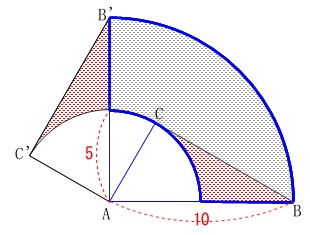四分円から四分円を引けば出てきます。
　\(\begin{eqnarray}
S&=&\frac{1}{4}\times \pi\,(\,10\,)^2-\frac{1}{4}\times \pi\,(\,5\,)^2\\
&=&\underline{\underline{　\frac{75}{4}\,\pi　}}
\end{eqnarray}\)

回転図形には同じ面積になる部分が出てくるので、
方向性としては非常に良いです。

少し解説不足かなと思えますが以上です。

⇒　滋賀県公立高校入試数学の問題と解説

過去問を見てわかる通り滋賀県の数学は手強いです。
しかし、基礎をしっかりおさえて作業を繰り返し応用すれば、
一つひとつの問題が深めの総復習になりますよ。