2022年(令和4年)度広島県公立高校入試の数学の問題と解説

2022年(令和4年)度広島県公立高校入試の数学の問題と解説です。
大問６問で構成された基本重視の問題です。
基本事項をおさえた上で数学で必要な作業を繰り返せば難問はありません。
文章題での読み取りに時間が多少必要なので、
他の問題で時間をかせいでおくと良いです。

2022年(令和4年)度広島県公立高校入試の数学の問題

令和４年度広島県公立高校入試の数学の問題です。

⇒　令和４年度広島県公立高校入試の数学の問題

大問６問の構成は例年通りです。

2022年(令和4年)度広島県公立高校入試の数学の解説

問題は\(\color{black}{\fbox{1}}\)から\(\color{black}{\fbox{6}}\)まであります。
時間は足りると思いますが、
基本問題を落とさないように注意しておきましょう。

第１問基本確認の小問集合

\(\color{black}{\fbox{1}}\)
(1)から(8)まであります。
基本問題ですが配点が割と高めなので、
ミスをしないように確実に取りましょう。

(1)
　\(\hspace{10pt}3-\color{red}{24\div (-4)}\\
=3\color{red}{+8}\\
=\underline{　11　}\)

符号に注意です。

(2)
　\(\hspace{10pt}3(4x+y)-5(x-2y)\\
=12x+3y-5x\color{red}{+10y}\\
=\underline{　7x+13y　}\)

２行目は暗算はしない方が確実です。
時間配分から暗算しても良いですが、
２巡目は確認すると良いですね。

(3)
　\(\hspace{10pt}\sqrt{45}-\sqrt{5}+\sqrt{20}\\
=\sqrt{3^2\times 5}-\sqrt{5}+\sqrt{2^2\times 5}\\
=3\sqrt{5}-\sqrt{5}+2\sqrt{5}\\
=\underline{　4\sqrt{5}　}\)

２行目のルートの中の素因数分解を暗算してミスする場合が多いです。

(4)
　\(\hspace{10pt}x^2y+4y\\
=y(x^2-4)\\
=\underline{　y(x+2)(x-2)　}\)

因数分解の第一歩は共通因数の抜き出しからです。

⇒　中学3年の因数分解公式まとめと典型的な応用問題の解き方

中学数学で使う因数分解の公式は少ないので覚えておきましょう。

(5)
ねじれの位置とは、
平行でもなく、交わりもしない、ということです。答え　\(\underline{　\,辺\,\mathrm{CF}\,,辺\,\mathrm{DF}\,,辺\,\mathrm{EF}　}\,\)

⇒　空間図形の位置関係問題(平行,ねじれの位置,垂直な面,平行な面)
　
延長して交わるものもねじれの位置とはなりませんが、
ここでは気にしなくて良いですね。

(6)
反比例の関数の比例定数を求めます。
　\(\hspace{10pt}\displaystyle y=\frac{a}{x}\)
点\(\,\mathrm{A\,(\,-3\,,\,2\,)}\,\)を通るとき
　\(\begin{eqnarray}\displaystyle
2&=&\frac{a}{-3}\\
a&=&\underline{　-6　}
\end{eqnarray}\)

反比例の関数は\(\,xy=a\,\)となるので
　\(\hspace{10pt}a=13\times 2=\underline{　-6　}\)
でも良いです。

⇒　比例と反比例の関数の比例定数を決める問題の解き方と座標の求め方

「比例定数」は比例\(\,y=ax\,\)のときだけ使う言葉ではないので注意が必要です。

(7)
角度を求める問題ですが、
合同の発見が先です。

３組の辺がそれぞれ等しいから
　\(\,\mathrm{△ABD}\,\)　≡　\(\,\mathrm{△CBD}\,\)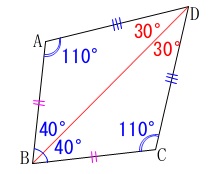三角形の内角の和から
　\(\hspace{4pt}\mathrm{∠ADB=∠CDB}=\color{red}{30^{\circ}}\)
なので
　\(\hspace{10pt}\mathrm{∠ADC}=\underline{　60　(度)　}\)

(8)
相対度数を求めます。
　\(\hspace{4pt}\displaystyle (\,相対度数\,)=\frac{　(\,階級の度数\,)　}{　(\,度数合計\,)　}\)

\(\,40\,\)以上\(\,50\,\)未満の階級の度数は\(\,\color{blue}{14}\,\)、
度数合計は\(\,\color{red}{40}\,\)なので
　\(\hspace{10pt}\displaystyle \frac{\color{blue}{14}}{\color{red}{40}}=\underline{　0.35　}\)

確率は分数ですが相対度数は小数で表すのが普通です。

⇒　度数分布表とは？階級の幅と階級値および累積度数とヒストグラム

資料の活用分野は教科書の内容が課程によってコロコロ変わりますが、
基本的なことは同じなので度数分布表は読み取れるようになっておきましょう。

第２問連立方程式と線分の長さと箱ひげ図

\(\color{black}{\fbox{2}}\)
(1)(2)(3)とありますがそれぞれ別問題です。

(1)
連立方程式の文章問題です。

混ぜ方が条件にあるので表で確認しておきます。
　\(\begin{array}{|c|c|c|} \hline
　ミルクティー　 & 　紅茶２　 & 　牛乳１　\\ \hline
　コーヒー牛乳　 & コーヒー１　&　牛乳１　\\ \hline
\end{array}\)

基本通り求めたいものを文字でおいて進めます。
　紅茶を\(\,x\,\)、コーヒーを\(\,y\,\)、牛乳と混ぜる。
（量の単位は\(\,\mathrm{mL}\,\)です。）
とすると
　\(\hspace{4pt}\displaystyle 紅茶\,x:\,牛乳\,\frac{1}{2}\,x\rightarrow ミルクティー\frac{3}{2}\,x\)
　\(\hspace{4pt}コーヒー\,y:牛乳\,y\rightarrow コーヒー牛乳\,2y\)
とになります。

条件は牛乳が全部で\(\,\mathrm{350}\,\)使い、
ミルクティーとコーヒー牛乳の量が同じなので
　\(\begin{cases}
\hspace{4pt}\displaystyle \frac{1}{2}\,x+y=350\\
\hspace{4pt}\displaystyle \frac{3}{2}\,x=2y
\end{cases}\)
これを解くと
　\(\hspace{4pt}x=280\,,\,y=210\)

答え　紅茶　\(\,\mathrm{\underline{　280\,(\,mL\,)}　}\,\)　コーヒー　\(\,\mathrm{\underline{　210\,(\,mL\,)}　}\,\)

連立方程式を解く方法はお任せします。

⇒　連立方程式の問題と解き方(加減法と代入法の選び方)

求めたいのは紅茶とコーヒーですが、
分数をさけたいので少し変形した形で文字設定することもできます。

紅茶に混ぜる牛乳を\(\,x\,\)とすると紅茶は\(\,2x\,\)、
コーヒーに混ぜる牛乳を\(\,y\,\)とするとコーヒーは\(\,y\,\)、
混ぜることになるので、
　\(\begin{cases}
\hspace{4pt}\displaystyle x+y=350\\
\hspace{4pt}\displaystyle 3x=2y
\end{cases}\)

これを解くと\(\,x=140\,,\,y=210\,\)と出てきます。
ただし、求めるのは紅茶とコーヒーなので、
　\(\hspace{4pt}2x=280\,,\,y=210\)
が答えになるので注意しておきましょう。

どちらでも良いですが、
答えが出たら条件に合っているか、確認はしましょう。

(2)
正四角すいの立体を扱いますが、
展開図における平面図形の問題です。

条件は問題文から読み取ってください。
点\(\,\mathrm{A}\,\)から点\(\,\mathrm{P}\,\)に糸をはるとき、
最も短くなるときの長さだと思えば良いです。

折れた線分が最も短くなるのは直線になるときです。
展開図で見れば明らかですよ。四角形\(\,\mathrm{OABC}\,\)はひし形なので相似も見えてきますが、
正三角形の\(\,60°\,\)を使って三平方の定理を利用したところです。
\(\,\mathrm{A}\,\)から直線\(\,\mathrm{OC}\,\)に垂線\(\,\mathrm{AT}\,\)を引くと、
三角定規の比から
　\(\hspace{4pt}\mathrm{OT}=\color{blue}{2}\,,\,\mathrm{AT}=\color{magenta}{2\sqrt{3}}\)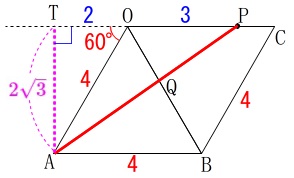よって、
三平方の定理から
　\(\begin{eqnarray}\displaystyle
\mathrm{AP^2}&=&\mathrm{AT^2+PT^2}\\
&=&(\color{magenta}{2\sqrt{3}})^2+\color{blue}{5}^2\\
&=&12+25\\
&=&37\\
\mathrm{AP}&=&\pm \sqrt{37}
\end{eqnarray}\)
長さなので\(\,\mathrm{AP\,＞\,0}\,\)だから
　\(\hspace{10pt}\mathrm{AP}=\underline{　\sqrt{37}　}\,(\,\mathrm{cm}\,)\)

このとき最小です。

(3)
箱ひげ図の問題です。

３年分のデータがありますが、
それぞれ３０日（個）のデータを箱ひげ図にしてあります。ざっくりですが問題になる数値に印を入れてあります。
①
２０１９年の第２四分位数（中央値）が１０００匹より左にあるので正しい。○
②
２０１９年も最大値が７０００匹より小さいので間違い。×
③
第１四分位数が３０００匹より小さく、
第３四分位数が１００００匹より大きいので断言はできない。×
（例えば第１四分位数と同じ日が１０日あったとしてもこの箱ひげ図はかける。）
④
２０２１年は少なくとも１５日はあります。
２０１９年は多くとも７日なので２倍はあります。○

答え　\(\,\underline{　①\,,\,④　}\,\)

四分位範囲は度数で区切っている事を忘れずに、
いくつか箱ひげ図を書いて練習すると良いですよ。
簡単に言えば中央値とその左右で中央値を探していく練習です。

第３問関数（文字設定）

\(\color{black}{\fbox{3}}\)
関数の問題ですが文字設定になれましょうか。
　関数は\(\hspace{4pt}\displaystyle y=\frac{1}{4}\,x^2\)と直線\(\,y=-3\,\)です。

問題の条件を図の中で確認しておきましょう。点\(\,\mathrm{A\,,\,B}\,\)はともに\(\,y=-3\,\)上の点です。

(1)
点\(\,\mathrm{A}\,\)の\(\,x\,\)座標が\(\,4\,\)のとき
\(\,\mathrm{△OBA}\,\)の面積が\(\,9\,\)になるのは、
高さが\(\,3\,\)なので底辺\(\,\mathrm{AB}\,\)の長さが\(\,6\,\)になるときです。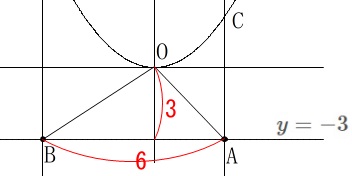底辺が\(\,6\,\)とすぐにでない人は底辺を\(\,\color{red}{a}\,\)とすると、
　\(\begin{eqnarray}\displaystyle
\frac{1}{2}\times a\times 3&=&9\\
3\,a&=&18\\
a&=&6
\end{eqnarray}\)
と三角形の面積計算から出せば良いですよ。
（無理な暗算はしないことです。）

点\(\,\mathrm{A}\,\)の\(\,x\,\)座標が\(\,4\,\)なので\(\,\mathrm{B}\,\)のx座標は\(\,-2\,\)ですね。

答え　\(\,x=\underline{　-2　}\,\)

ここでも文字設定は使えます。
点\(\,\mathrm{B}\,\)の座標を\(\,(\,t\,,\,-3\,)\,\)とすると
　\(\hspace{4pt}\mathrm{AB}=\color{red}{4-t}\)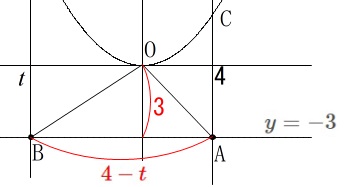高さは\(\,\color{red}{3}\,\)なので
　\(\begin{eqnarray}\displaystyle
\frac{1}{2}\times \mathrm{AB}\times 3&=&9\\
\frac{1}{2}\times (4-t)\times 3&=&9\\
t&=&\underline{　-2　}
\end{eqnarray}\)
点\(\,\mathrm{B}\,\)の\(\,x\,\)座標が負であることに適しています。

計算が雑ですが１次方程式です。

(2)
四角形\(\,\mathrm{DBAC}\,\)が正方形になるときの点\(\,\mathrm{A}\,\)の座標を全て求めます。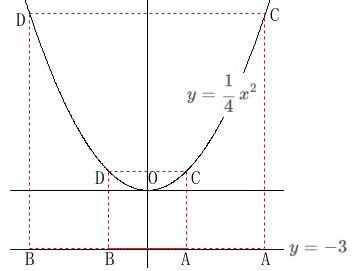結果からいうと２つあります。

いくつもできそうですが計算すると２つだと分かりますので見ていきましょう。
文字設定で進めます。

今度は点\(\,\mathrm{A}\,\)も定まってはいません。
ただし、点\(\,\mathrm{B}\,\)の\(\,y\,\)座標が\(\,\mathrm{A}\,\)と同じでることは変わりませんよ。

四角形\(\,\mathrm{BDAC}\,\)が正方形になるためには、
「長方形」かつ「ひし形」なので
平行四辺形でもなくてはならないので点\(\,\mathrm{C\,,\,D}\,\)は同じ\(\,y\,\)座標となります。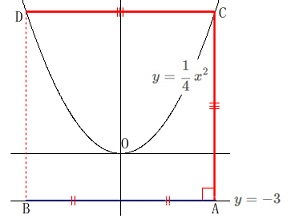つまり\(\,\mathrm{DC}\,\)は\(\,\mathrm{AB}\,\)に平行になります。

点\(\,\mathrm{A}\,\)の座標を\((\,t\,,\,-3\,)\)とすると、
（\(\,x\,\)座標は正なので\(\,t\,＞\,0\,\)）
点\(\,\mathrm{B}\,\)は\(\,y\,\)軸で対称になるので
（でなければ\(\,\mathrm{C\,,\,D}\,\)が同じ\(\,y\,\)座標にならない。）
　\(\hspace{4pt}\mathrm{B}\,(\,-t\,,\,-3)\,\)
このとき\(\,\mathrm{C\,,\,D}\,\)は放物線上の点なので、
　\(\hspace{4pt}\displaystyle \mathrm{C}\,\left(\,t\,,\,\frac{1}{4}\,t^2\,\right)\,\)
　\(\hspace{4pt}\displaystyle \mathrm{D}\,\left(\,\,-t\,,\,\frac{1}{4}\,t^2,\right)\,\)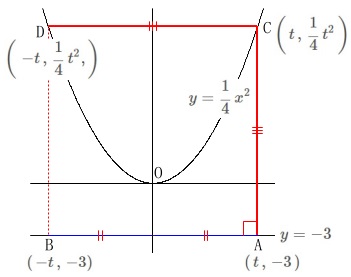正方形を満たす条件は
　\(\begin{eqnarray}\displaystyle
\mathrm{AB}&=&\mathrm{AC}\\
t-(-t)&=&\frac{1}{4}\,t^2-(-3)\\
2t&=&\frac{1}{4}\,t^2+3\\
8t&=&t^2+12\\
t^2-8t+12&=&0\\
(t-2)(t-6)&=&0\\
t&=&2\,,\,6
\end{eqnarray}\)
条件に適していますね。

答え　\(\,x=\underline{　2\,,\,6　}\,\)

第４問半円と平行線（相似の証明）

\(\color{black}{\fbox{4}}\)
相似の証明です。
　\(\,\mathrm{△AEC}\,\)　∽　\(\,\mathrm{△ABD}\,\)

問題文にある条件から相似条件を探しましょう。

問題文にある条件
　線分\(\,\mathrm{AB}\,\)を直径とする半円
　点\(\,\mathrm{O}\,\)は線分\(\,\mathrm{AB}\,\)の中点（円の中心）
　\(\,\mathrm{AC}\,\)∥\(\,\mathrm{OD}\,\)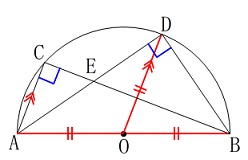直径に対する円周角が\(\,90°\,\)で等しいことはすぐに気がつくでしょう。

平行線の錯角や同位角が等しいこと、
半径は常に等しいことから、
\(\,\mathrm{△OAD}\,\)が二等辺三角形であることから底角が等しくなるを図に示します。相似条件が出そろいました。

まとめておいてください。
書き方は好きにしていいです。

⇒　中学の図形証明問題(合同･相似)の解き方と証明の書き方ポイント

図の中で証明を終わらせておく、
というのがポイントです。

第５問１次関数の文章題

\(\color{black}{\fbox{5}}\)
長い長い日本語が書かれた１次関数の問題です。

数学に必要な言葉は少しで、
グラフも与えてくれていますのでちゃちゃっと終わらせます。

要は、
ドローンは同じ速さ（分速\(\,\mathrm{1.2\,km}\,\)）で\(\,\mathrm{12\,km}\,\)を往復する。
荷物を載せないときは表１と図１、
荷物を運ぶときは表２と図２のバッテリー消費だということですね。
※
荷物は\(\,5\,\mathrm{kg}\,\)のときしか考えないので関係ありません。

読み取りしても良いのですが、
会話の中で通る点を与えてくれているので必要ありません。

荷物を載せないとき
　\(\hspace{4pt}(\,0\,,\,100\,)\)
　\(\hspace{4pt}(\,4\,,\,92\,)\)
の２点を通るので
　\(\hspace{10pt}y=-2\,x+100\)

荷物を載せるとき
　\(\hspace{4pt}(\,0\,,\,100\,)\)
　\(\hspace{4pt}(\,4\,,\,82\,)\)
の２点を通るので
　\(\hspace{10pt}\displaystyle y=-\frac{9}{2}\,x+100\)

関数はこの２つですが荷物を載せるのが先か後かで、
バッテリーの消費状態は変わるので必要なのは傾きです。

(1)
２点を通る直線の式を表せば良いのですでにでています。
　\(\hspace{10pt}\underline{　y=-2\,x+100　}\)

(2)
移動距離と速さの関係から\(\,10\,\)分間で荷物を届けて、
\(\,10\,\)分間で戻ってきます。

これをグラフにすると、
届けるときの傾きは\(\displaystyle \,-\frac{9}{2}\,\)、
戻るときの傾きは\(\,-2\,\)です。

つまり、バッテリーの消費は、
荷物を積んで移動した\(\,10\,\)分間で\(\,45\,\)％、
荷物を積まずに移動した\(\,10\,\)分間で\(\,20\,\)％、
ということです。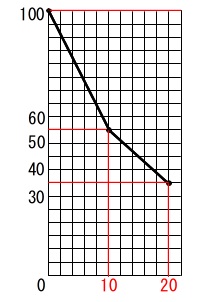\(\,20\,\)分間で消費したバッテリーは\(\,65\,\)％で、
残量\(\,30\,\)％以上なので利用できる。

第６問確率

\(\color{black}{\fbox{6}}\)
(1)と(2)でルールが変わるので注意しましょう。

カードは\(\color{black}{\fbox{1}}\)、\(\color{black}{\fbox{2}}\)、\(\color{black}{\fbox{3}}\)、\(\color{black}{\fbox{4}}\)が１枚ずつ。
移動は四角形\(\,\mathrm{ABCD}\,\)の頂点を反時計回り。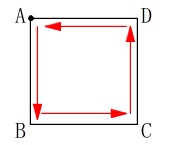出発点は\(\,\mathrm{A}\,\)です。

太郎さん、次郎さんの順にカードを取り出すのは同じです。
(1)
〈ルール〉
①　取り出したカードの数字だけ反時計回りに移動する。
②　取り出したカードを袋に戻す。
③　①で移動した点から取り出した数字だけ反時計回りに移動する。
④　\(\,\mathrm{Ⅰ}\,\)から\(\,\mathrm{Ⅳ}\,\)の状態で勝敗を決める。
　\(\begin{array}{|c|c|c|c|} \hline
&　①の位置　&　③の位置　& 勝敗 \\ \hline
Ⅰ & \mathrm{B} & \mathrm{B} & 引き分け\\ \hline
Ⅱ & \mathrm{B} & \mathrm{A\,,\,C\,,\,D\,} &　太郎さんの勝ち　\\ \hline
Ⅲ & \mathrm{A\,,\,C\,,\,D\,} & \mathrm{B} & 次郎さんの勝ち\\ \hline
Ⅳ & \mathrm{A\,,\,C\,,\,D\,} & \mathrm{A\,,\,C\,,\,D\,} & 引き分け\\ \hline
\end{array}\)
問題文に「例えば」とある部分は、
どういう動きをするかを確認できます。
この手の問題では必ず試しておくことですよ。

太郎さんが点\(\,\mathrm{B}\,\)の位置に移動するのは、
\(\color{black}{\fbox{1}}\)のカードを取り出したときだけです。
答え　\(\hspace{4pt}\displaystyle \underline{　\frac{1}{4}　}\)

このルールではどちらが勝つかは確率が同じです。
問題に書いてあるので必要ありませんが確かめておきます。

樹形図の方が簡単ですが表で見ていくことにします。

赤が太郎さんが引いた数字、
青が次郎さんが引いた数字だとみてください。
枠内の記号は太郎さんが移動した点と次郎さんが移動した点を書き込みます。
　\(\begin{array}{|c|c|c|c|c|} \hline
&　 \color{red}{1}　 &　 \color{red}{2}　 &　 \color{red}{3}　 & 　\color{red}{4}　 \\ \hline
　\color{blue}{1}　 & \mathrm{\color{red}{B\,C}} & \mathrm{C\,D} & \mathrm{D\,A} & \mathrm{\color{blue}{A\,B}}\\ \hline
\color{blue}{2} & \mathrm{\color{red}{B\,D}} & \mathrm{C\,A} & \mathrm{\color{blue}{D\,B}} & \mathrm{A\,C}\\ \hline
\color{blue}{3} & \mathrm{\color{red}{B\,A}} & \mathrm{\color{blue}{C\,B}} & \mathrm{D\,C} & \mathrm{A\,D}\\ \hline
\color{blue}{4} & \mathrm{B\,B} & \mathrm{C\,C} & \mathrm{D\,D} & \mathrm{A\,A}\\ \hline
\end{array}\)

太郎さんが勝つのは前の文字が\(\,\mathrm{B}\,\)、
後ろの文字が\(\,\mathrm{A\,,\,C\,,\,D}\,\)の組合わせなので確率は\(\,\displaystyle \frac{3}{16}\,\)、
次郎さんが勝つのは前の文字が\(\,\mathrm{A\,,\,C\,,\,D}\,\)、
後ろの文字が\(\,\mathrm{B}\,\)の組合わせなので確率は\(\,\displaystyle \frac{3}{16}\,\)で同じです。
（\(\,\mathrm{B}\,\)だけに着目すると探しやすいです。）

樹形図だと太郎さんが\(\,\mathrm{B}\,\)に移動するのは\(\color{black}{\fbox{1}}\)を引いたときだけなので、
やってみると確率は出しやすいと思いますよ。

次はルールが少し変わります。

(2)
(1)のルールの\(\,②\,\)が
\(\,②’\,\)「取り出したカードを戻さない」に変わります。
〈ルール〉
①　取り出したカードの数字だけ反時計回りに移動する。
②’　取り出したカードを袋に戻さない。
③　①で移動した点から取り出した数字だけ反時計回りに移動する。
④　\(\,\mathrm{Ⅰ}\,\)から\(\,\mathrm{Ⅳ}\,\)の状態で勝敗を決める。
　\(\begin{array}{|c|c|c|c|} \hline
&　①の位置　&　③の位置　& 勝敗 \\ \hline
Ⅰ & \mathrm{B} & \mathrm{B} & 引き分け\\ \hline
Ⅱ & \mathrm{B} & \mathrm{A\,,\,C\,,\,D\,} &　太郎さんの勝ち　\\ \hline
Ⅲ & \mathrm{A\,,\,C\,,\,D\,} & \mathrm{B} & 次郎さんの勝ち\\ \hline
Ⅳ & \mathrm{A\,,\,C\,,\,D\,} & \mathrm{A\,,\,C\,,\,D\,} & 引き分け\\ \hline
\end{array}\)
勝敗の条件は変わらないので見方は同じですが、
取り出したカードを戻さないので、
（同じ数字は出てこない。）
表では表れない部分ができます。
　\(\begin{array}{|c|c|c|c|c|} \hline
&　 \color{red}{1}　 &　 \color{red}{2}　 &　 \color{red}{3}　 & 　\color{red}{4}　 \\ \hline
　\color{blue}{1}　 & × & \mathrm{C\,D} & \mathrm{D\,A} & \mathrm{\color{blue}{A\,B}}\\ \hline
\color{blue}{2} & \mathrm{\color{red}{B\,D}} & × & \mathrm{\color{blue}{D\,B}} & \mathrm{A\,C}\\ \hline
\color{blue}{3} & \mathrm{\color{red}{B\,A}} & \mathrm{\color{blue}{C\,B}} & × & \mathrm{A\,D}\\ \hline
\color{blue}{4} & \mathrm{B\,B} & \mathrm{C\,C} & \mathrm{D\,D} & ×\\ \hline
\end{array}\)

先に取り出した人（太郎さん）が勝つ確率は
　\(\hspace{10pt}\,\displaystyle \frac{2}{12}=\frac{1}{6}\)
後に取り出した人（次郎さん）が勝つ確率は
　\(\hspace{10pt}\,\displaystyle \frac{3}{12}=\frac{1}{4}\)

答え　\(\,\underline{　ウ　}\,\)

(1)(2)ともに\(\,\mathrm{A}\,\)を\(\,0\,\)として
\(\,\mathrm{B\,,\,C\,,\,D}\,\)に数字を付けて、
２人の数字の和で考えることもできます。
一人目の数字の状態は見ておく必要がありますが、
樹形図で確認していくと分かり易いですよ。

以上です。

⇒　広島県公立高校入試数学の問題と解説

数年分見直して、自分でやってみてください。
数学の基本をどれだけ重視しているかがよく分かります。