令和4年度(2022年)滋賀県公立高校入試【数学】の問題と解説です。
偏りの少ない問題構成ですが比較的図形色の濃い問題になっています。
応用問題もありますがヒントもくれているので、
基礎の習得はもちろん大切ですが、作業をしっかりすることで対応できます。
令和4年(2022年)度滋賀県公立高校入試【数学】の問題
滋賀県公表の令和4年(2022年)度滋賀県公立高校入試【数学】の問題です。
⇒ 令和4年(2022年)度滋賀県公立高校入試【数学】の問題PDF
解答用紙、正答例もそのまま載せておきますので、
注意書き等にも目を通しておくと本番で役に立つこともあります。
令和4年(2022年)度滋賀県公立高校入試【数学】の解説
例年同様大問4つで構成されていて、
傾向は変わっていませんので早速解説に入ります。
第1問
\(\color{black}{\fbox{\(\,\large{1}\,\)}}\)
式の計算から確率、関数、データなど、
(1)から(9)までの小問があります。
(1)
\(\hspace{10pt}12-6\div (-3)\\
=12-(-2)\\
=\underline{ 14 }\)
掛け算割り算が先です。
(2)
\(\hspace{10pt}\displaystyle \frac{1}{2}\,a-\frac{4}{3}\,a\\
\displaystyle =\frac{3a-8a}{6}\\
\displaystyle =\underline{\underline{ -\frac{5}{6}\,a }}\)
通分して分子の計算に集中ですね。
(3)
代入問題です。
\(\hspace{4pt}\mathrm{A}=4x-1\,,\,\mathrm{B}=-2x+3\)
\(\hspace{10pt}\mathrm{-4A+3B+2A}\\
=-2\mathrm{A}+3\mathrm{B}\\
=-2(4x-1)+3(-2x+3)\\
=-8x+2-6x+9\\
=\underline{ -14\,x+11 }\)
⇒ 式の計算(中学2年) 文字式に数値を代入する問題を解くときのポイント
代入するときのコツは確認しておきましょう。
(4)
\(\hspace{10pt}-15a^2b\div 3ab^2\times (-2b)^2\\
\displaystyle =-\frac{15a^2b\times 4b^2}{3ab^2}\\
=\underline{ -20\,a\,b }\)
全体の符号を考えて割り算部分を分母に回しました。
(5)
\(\hspace{10pt}(\sqrt{2}-\sqrt{3})^2+\sqrt{6}\\
=2-2\sqrt{6}+3+\sqrt{6}\\
=\underline{ 5-\sqrt{6} }\)
どこまで暗算するかは人それぞれですが、
ミスはもったいないのでできるだけ暗算はさけておきましょう。
(6)
2次方程式を解きます。
\(\hspace{10pt}x^2=x+12\)
因数分解から試します。
\(\begin{eqnarray}\displaystyle
x^2-x-12&=&0\\
(x+3)(x-4)&=&0\\
x&=&\underline{ -3\,,\,4 }
\end{eqnarray}\)
因数分解できない場合は解の公式です。
(7)
関数の変域問題です。
\(\hspace{4pt}y=-3\,x^2\,\hspace{4pt}(\,-4\,≦\,x\,≦\,3\,)\)
における\(\,y\,\)の変域です。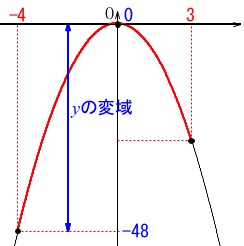
答え \(\underline{ -48\,≦\,y\,≦\,0 }\)
簡単にで良いのでグラフを書いて見ます。
\(\,x=-3\,\)の\(\,y\,\)値は変域には関係ありません。
(8)
2枚のカードを引く確率です。
2の倍数ではなく、3の倍数でもない?
積なので2の倍数や3の倍数があってはダメですね。
同時に2枚引くのと1枚ずつ2回引くのは同じと考えて、
1枚目と2枚目で場合を考えましょう。
(赤、青どちらが1枚目でも同じです。)
樹形図で良いですが表で見ます。
\(\begin{array}{|c|c|c|c|c|} \hline
& \,\color{red}{3}\, & \,\color{red}{4}\, & \,\color{red}{5}\, & \,\color{red}{6}\, & \,\color{red}{7}\,\\ \hline
\,\color{blue}{3}\, & × & & & & \\ \hline
\,\color{blue}{4}\, & & × & & & \\ \hline
\,\color{blue}{5}\, & & & × & & ○\\ \hline
\,\color{blue}{6}\, & & & & × & \\ \hline
\,\color{blue}{7}\, & & & & ○ & ×\\ \hline
\end{array}\)
同時に引くので同じ数はありません。
\(\hspace{4pt}\displaystyle \frac{2}{20}=\underline{\underline{ \frac{1}{10} }}\)
次いきます。
(9)
度数分布表の読み取りからの計算問題です。
1つの階級(\(\,10\,\)以上\(\,20\,\)未満)の相対度数が等しい。
相対度数は
\(\hspace{4pt}\displaystyle \frac{ 度数 }{ 度数合計 }\)
なので\(\,\mathrm{B}\,\)中学校の度数を\(\,x\,\)とすると
\(\begin{eqnarray}\displaystyle
\frac{66}{220}&=&\frac{x}{60}\\
220\,x&=&66\times 60\\
x&=&\frac{66\times 60}{220}\\
&=&\underline{ 18 }
\end{eqnarray}\)
相対度数を計算する必要はありませんが、
計算しても別に構いません。
第2問
\(\color{black}{\fbox{\(\,\large{2}\,\)}}\)
1次関数のグラフについての問題です。
コンピューターを使おうが手書きであろうが、
関係ありませんのでクラフから読み取りをしましょう。
(1)
グラフが図1の状態にあるとき
傾き\(\,a\,\)と\(\,3a+b\,\)の値をざっくり見ます。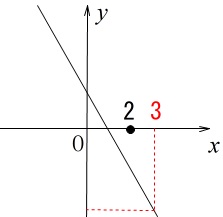 右下がりのグラフなので傾き\(\,a\,\)は負、
右下がりのグラフなので傾き\(\,a\,\)は負、
\(\,x=3\,\)のとき\(\,3a+b\,\)なので明らかに負となっています。
答え \(\,a \underline{ 負の値 } 3a+b \underline{ 負の値 }\,\)
(2)
2つの直線で傾きと切片を変化させます。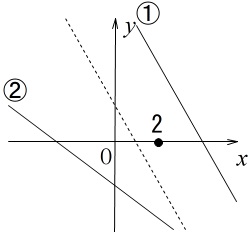 ①は図1のグラフを平行移動しているので傾きは同じです。
①は図1のグラフを平行移動しているので傾きは同じです。
問題に書いてあるように\(\,y\,\)軸の正の方向への平行移動なので、
切片\(\,b\,\)は大きくしています。
②は傾きが負のままなのでわかりにくいかもしれませんが、
下がり方が少なくなっているので傾き\(\,a\,\)は大きくなり、
(例えば傾き\(\,-3\,\)から\(\,-1\,\)となるのは大きくなっています。)
切片は下に移動しているので\(\,b\,\)は小さくなっています。
どのように変えたかなので、
答え \(\,aの値は \underline{ 大きくする } bの値は \underline{ 小さくする }\,\)
(3)
図形を座標上で考える問題です。
4点があり、
3点\(\,\mathrm{B\,,\,C\,,\,D}\,\)は固定されていて、
\(\,\mathrm{B}\,(\,1\,,\,2\,)\,,\,\mathrm{C}\,(\,4\,,\,0\,)\,,\,\mathrm{D}\,(\,-3\,,\,-2\,)\,\)
点\(\,\mathrm{A}\,\)だけが\(\,y=-x\,\)上を動きます。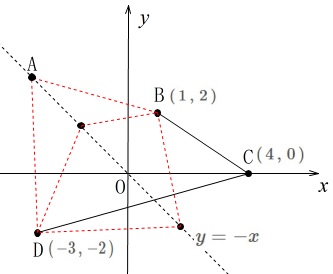 4点でできる図形が三角形になるのは、
4点でできる図形が三角形になるのは、
点\(\,\mathrm{A}\,\)が直線\(\,\mathrm{BD}\,\)か、\(\,\mathrm{CB}\,\)上にあるときです。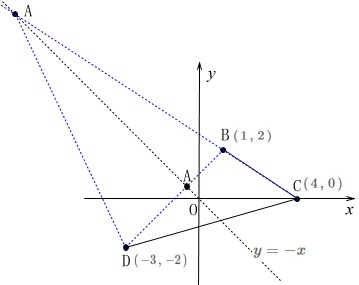 このとき、
このとき、
\(\,\mathrm{△BDC=S\,,\,△ADC=T}\,\)となります。
具体的な面積も出せますが必要ありません。
ただし、点\(\,\mathrm{A}\,\)が直線\(\,\mathrm{BC}\,\)上にあるときの座標は求めておきます。
直線\(\,\mathrm{BC}\,\)は2点
\(\hspace{4pt}\mathrm{B}\,(\,1\,,\,2\,)\,,\,\mathrm{C}\,(\,4\,,\,0\,)\)
を通る直線なので、
\(\hspace{10pt}\displaystyle y=-\frac{2}{3}\,x+\frac{8}{3}\)
直線(1次関数)の求め方は確認しておいて下さい。
直線\(\,y=-x\,\)との交点は
\(\hspace{10pt}\mathrm{A}\,\color{red}{(\,-8\,,\,8\,)}\)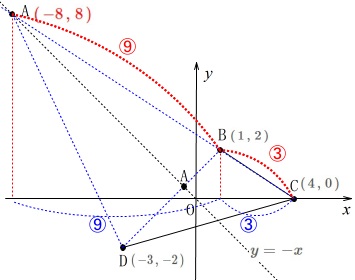 \(\,x\,\)座標の差分から比を考えて
\(\,x\,\)座標の差分から比を考えて
(\(\,y\,\)座標の差分でも同じです。)
\(\hspace{10pt}\mathrm{BC:AB}=\color{red}{3}:\color{red}{9}\)
よって
\(\begin{eqnarray}\displaystyle
\mathrm{△BDC:△ADC}&=&\mathrm{S:T}\\
&=&\color{red}{3}:(\color{red}{3}+\color{red}{9})\\
&=&3:12\\
&=&\underline{ 1:4 }
\end{eqnarray}\)
※
点\(\,\mathrm{A}\,\)が\(\,\mathrm{BD}\,\)上にあるときの座標は必要無いことと、
面積比は\(\,\mathrm{BC:AB}\,\)でないことに注意すれば問題ないでしょう。
(面積比は\(\,\mathrm{BC:AC}\,\)です。)
(4)
今度は点\(\,\mathrm{A}\,\)も固定されます。
\(\hspace{10pt}\mathrm{A}\,(\,2\,,\,-2\,)\)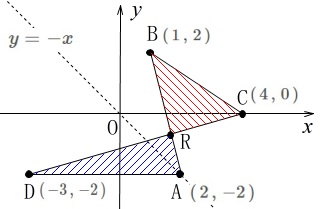 このとき
このとき
\(\hspace{10pt}\mathrm{△RAD=△RBC}\)
となることを説明します。
これは等積移動で簡単に説明できますね。
直線\(\,\mathrm{BD}\,\)は2点\(\,(\,-3\,,\,-2\,)\,,\,(\,1\,,\,2\,)\,\)を通るので、
\(\hspace{10pt}y=x+1\)
直線\(\,\mathrm{AC}\,\)は2点\(\,(\,2,,\,-2\,)\,,\,(\,4\,,\,0\,)\,\)を通るので、
\(\hspace{10pt}y=x-4\)
2本の直線は傾きが等しく平行です。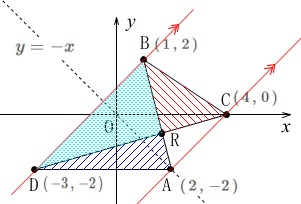 このとき
このとき
\(\hspace{10pt}\mathrm{△BAD=△BCD}\)
\(\,\mathrm{△BDR}\,\)を共通に持つ三角形なので、
\(\hspace{10pt}\mathrm{△RAD=△RBC}\)
交点\(\,\mathrm{R}\,\)の座標も出るので、
具体的な面積で等しいことを説明しても良いです。
※
会員は面積計算が短時間で出せると思うのでどちらでも良いです。
解答上では交点\(\,\mathrm{R}\,\)の座標を求めて、
「面積が~、で等しい。」
とでも書いておけば良いですよ。
(採点者を悩ませるかもしれませんが高校の先生なら大丈夫でしょう。)
次いきましょう。
第3問
\(\color{black}{\fbox{\(\,\large{3}\,\)}}\)
方程式、連立方程式です。
と見せかけての立体の対角線問題もあります。
(1)
先ずは方程式です。
変化していないのはルールパンの数なので、
ロールパンを表す文字式を等号で結びます。
\(\,x\,\)人に配るとするとロールパンの数は
「4個ずつ配ると9個余る」は\(\,4x+9\,\)
「6個ずつ配ると5個足りない」は\(\,6x-5\,\)
と表せるので、(過不足を考えて)
\(\begin{eqnarray}\displaystyle
4x+9&=&6x-5\\
2x&=&14\\
x&=&\underline{ 7 }\,(\,人\,)
\end{eqnarray}\)
(2)
連立方程式ですが、
ロールパン6個を1セットとしておきます。
作るのに必要とする小麦粉とバターの量を表にすると
\(\begin{array}{|c|c|c|} \hline
& 小麦粉 & バター \\ \hline
食パン1斤 & 300 & 10 \\ \hline
ロールパン1セット & 150 & 10 \\ \hline
\end{array}\)
※単位は\(\,\mathrm{g}\,\)です。
小麦粉は\(\,1500\,\)、バターは\(\,80\,\)を使い切るので、
食パン\(\,x\,\)斤、ロールパン\(\,y\,\)セット作るとすると
\( \begin{cases}
\hspace{4pt} 300x+150y=1500\\
\hspace{4pt} 10x+10y=80
\end{cases}\)
これから
\(\hspace{10pt}x=2\,,\,y=6\)
となりますがロールパンはセット数なので注意しておきましょう。
答え \(\,食パン\underline{ 2 }斤\,,\,ロールパン\underline{ 36 }個\,\)
(3)
対角線の長さを求めます。
(1)(2)はつながっているようで、関係はありません。
図3の対角線\(\,\mathrm{FH}\,\)の長さを求めれば良いだけなので、
切り替えましょう。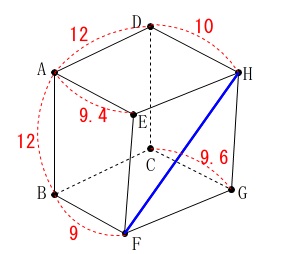 ※
※
長さの単位は\(\,\mathrm{cm}\,\)です。
難しく考えなくて良いですよ。
平行四辺形になるのは直方体を平面で切っただけです。
直方体の対角線ですよ。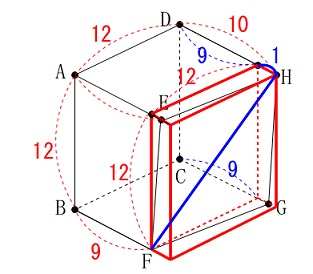 一番長い辺と短い辺に着目すれば直方体ができます。
一番長い辺と短い辺に着目すれば直方体ができます。
その直方体の対角線なので
\(\begin{eqnarray}\displaystyle
\mathrm{FH^2}&=&12^2+1^2+12^2\\
&=&144+1+144\\
&=&289\\
&=&17^2
\end{eqnarray}\)
\(\,\mathrm{FH>0}\,\)なので
\(\hspace{10pt}\mathrm{FH}=\underline{ 17 }\,(\,\mathrm{cm}\,)\)
素因数分解が素数の積なので、
覚えてなければ少じ時間がかかるかもしれませんね。
次いきます。
第4問
\(\color{black}{\fbox{\(\,\large{4}\,\)}}\)
この問題は、
「先生のアドバイス」がなければ大学入試でも得点差が出るでしょうね。
ただ、ここでは問題をよく読めば難しくはありません。
(1)
2つの点が移動する距離の合計です。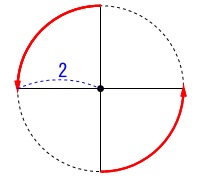 「距離」ですがここでは直線ではなく、
「距離」ですがここでは直線ではなく、
図の形状から弧の長さを意味しているようですね。
陸上競技のトラックと同じです。
(『距離』についてはあいまいなところもあるので「長さ」として欲しいところです。)
\(\,\mathrm{B\,,\,C}\,\)それぞれ半径\(\,\color{blue}{2}\,\mathrm{m}\,\)の円周上を\(\,90°\,\)移動するので、
合計は2つの移動の和になるから
\(\hspace{10pt}\displaystyle 2\,\pi\,(\,\color{blue}{2}\,)\times \frac{90}{360}\times \color{red}{2}\\
=\underline{ 2\,\pi }\,(\,\mathrm{m}\,)\)
(2)
辺の長さが等しいことの証明です。
先ずは合同の証明ですが、
図3の条件を図の中で確認していきましょう。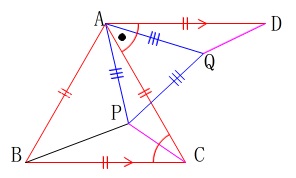 問題にある条件を書き込むと図のようになります。
問題にある条件を書き込むと図のようになります。
四角形\(\,\mathrm{ABCD}\,\)はひし形ですが使わないかな?
辺の長さは明らかなので説明しませんが、
\(\,\mathrm{AD}\,\)∥\(\,\mathrm{BC}\,\)
から錯角が等しくなるので
\(\hspace{4pt}\mathrm{∠ACB=∠CAD}\)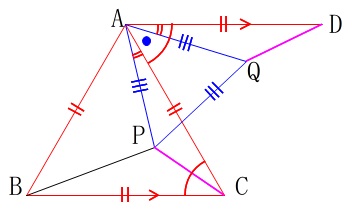 正三角形の1つの角から共通の\(\,\mathrm{\color{blue}{∠CAQ}}\,\)を引くことになるので
正三角形の1つの角から共通の\(\,\mathrm{\color{blue}{∠CAQ}}\,\)を引くことになるので
\(\hspace{4pt}\mathrm{\color{red}{∠PAC}=\color{red}{∠QAD}}\)
よって、
「2組の辺とその間の角がそれぞれ等しい。」
という合同条件がそろいます。
\(\,\mathrm{△PAC}\,\)≡\(\,\mathrm{△QAD}\,\)
合同な図形の対応する辺は等しいので、
\(\hspace{10pt}\mathrm{CP=DQ}\)
大した証明では無いので書き方は好きにして下さい。
⇒ 中学の図形証明問題(合同・相似)の解き方と証明の書き方ポイント
合同は相似でもあるので証明は同じ方法です。
(どちらかというと相似の方が条件が少ない。)
(3)
点\(\,\mathrm{A\,,\,B\,,\,C}\,\)が動く距離の合計
\(\hspace{4pt}\mathrm{AP+BP+CP=BP+PQ+QD}\)
が最も短くなるときの値を求めます。
(3)重心となることを利用する方法
正三角形なので直感的に点\(\,\mathrm{P}\,\)が重心のときで
(重心が中線を\(\,\color{magenta}{2}:\color{magenta}{1}\,\)に分けることから)
\(\begin{eqnarray}\displaystyle
\mathrm{AP}&=&\frac{2}{3}\times \mathrm{\color{blue}{AM}}\\
&=&\frac{2}{3}\times \color{blue}{2\sqrt{3}}\\
\end{eqnarray}\)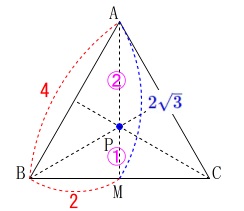 求める長さは3つ分になるから
求める長さは3つ分になるから
\(\hspace{10pt}\mathrm{AP+BP+CP}\\
\displaystyle =3\times \frac{2}{3}\times \color{blue}{2\sqrt{3}}\\
=\underline{ 4\sqrt{3} }\,(\,\mathrm{cm}\,)\)
としても正解です。
というのも、問題の続きを読んで聞くと、
「先生のアドバイス2」
に書いてあります。
※
あきらめずに取り組んでみると良いことあります。
(あきらめるにしても問題読む時間くらいは取りたい。)
(3)平行四辺形の対角線として求める方法
直感的でない?方法で解くとすれば、
平行四辺形(ひし形)の対角線を求める方法があります。
\(\hspace{4pt}\mathrm{AP+BP+CP=BP+PQ+QD}\)
なので折れ線としている
\(\hspace{10pt}\mathrm{BP+PQ+QD}\)
が直線になるときなので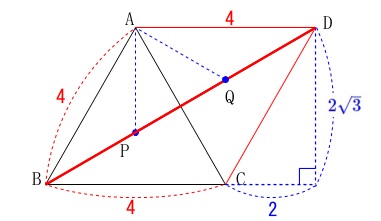 求める値は三平方の定理から
求める値は三平方の定理から
\(\begin{eqnarray}\displaystyle
\mathrm{BD^2}&=&(\color{red}{4}+\color{blue}{2})^2+(\color{blue}{2\sqrt{3}})^2\\
&=&6^2+(2\sqrt{3})^2\\
&=&36+12\\
&=&48
\end{eqnarray}\)
\(\,\mathrm{BD\,>\,0}\,\)なので
\(\hspace{10pt}\mathrm{BD}=\underline{ 4\sqrt{3} }\,(\,\mathrm{cm}\,)\)
問題の誘導からするとこちらですね。
どっちでも良いです。
(4)
作図です。
先生のアドバイスでは、
『3つの角の大きさがすべて\(\,120°\,\)となるとき』
とあるので\(\,120°\,\)の作図ですね。
目的は
\(\,\mathrm{∠BRC=∠BRT=∠CRT=120^{\circ}}\,\)
となる\(\,\mathrm{R}\,\)を示すことです。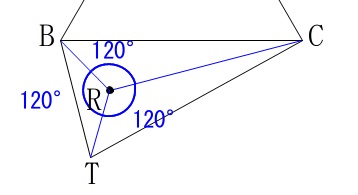 \(\,\mathrm{△ABC}\,\)は正三角形なので、
\(\,\mathrm{△ABC}\,\)は正三角形なので、
点\(\,\mathrm{P}\,\)は\(\,\mathrm{△ABC}\,\)の重心になりますが、
3点\(\,\mathrm{A\,,\,B\,,\,C}\,\)から等しい距離にあるので円の中心でもあります。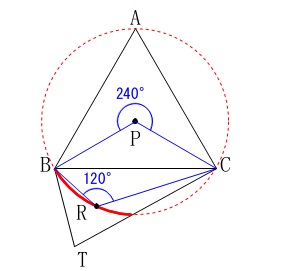 ※
※
問題の図4は印刷すると点\(\,\mathrm{P}\,\)が中心からずれていますので注意。
(印刷設定かな?)
弧\(\,\mathrm{BAC}\,\)に対する中心角が\(\,240°\,\)なので、
図の赤の太線上にあれば円周角\(\,120°\,\)になるので、
点\(\,\mathrm{R}\,\)は赤の太線上にあるはずです。
(線分\(\,\mathrm{BC}\,\)の条件と先生のアドバイス②から点\(\,\mathrm{R}\,\)は\(\,\mathrm{△BTC}\,\)の内部。)
後は\(\,\mathrm{∠CRT}\,\)を\(\,120°\,\)とすれば良いので、
\(\,\mathrm{△CBT}\,\)は二等辺三角形だから、
頂角を2等分するので点\(\,\mathrm{C}\,\)から\(\,\mathrm{BT}\,\)に垂線を引けば作図が完成します。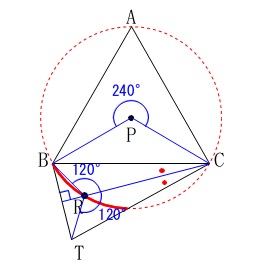
垂線は\(\,\mathrm{∠BCT}\,\)の二等分線でも良いですし、
普通に垂線でも良いですし、
ひし形の対角線でも良いですね。
ひし形を使うと作図が楽なのでひし形にします。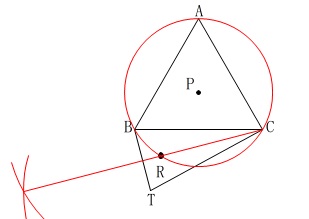 赤線が解答となる作図です。
赤線が解答となる作図です。
もちろん角の二等分線や垂線でも正解ですのでお好きな作図でどうぞ。
あ、解答欄の都合でひし形が描けないので垂線か二等分線が良いです。w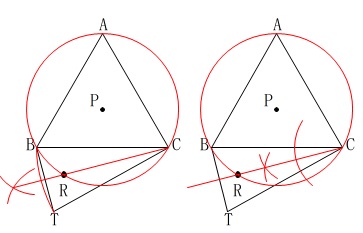 解答用紙でも点\(\,\mathrm{P}\,\)が中心からずれるので印刷設定かな?
解答用紙でも点\(\,\mathrm{P}\,\)が中心からずれるので印刷設定かな?
まあいいや、気にしないでおきます。
ここは傾向と対策をするところではありませんが、
滋賀県の県立入試では作図を図形総合として出題する傾向かもしれません。
作図は図形的な基礎知識がなければできませんからね。
かなり応用されているように見えますが図形総合問題ですよ。
急いで書き上げたので少し説明が足りないような気もしますが以上です。
※
間違いなど気がついたらご指摘頂けると幸いです。
昨年度の問題でも作図の正答率が低かったです。
図形をきっちり仕上げておくか、
作図を捨てるか、あなたはどうしますか?
私なら『覚え太郎』『超え太郎』を何度も復習します。
オリジナル作図問題集『さくっと!』もあるしね。
