2022年（令和4年）度和歌山県公立高校入試【数学】の問題と解説

２０２２年（令和４年）度和歌山県公立高校入試【数学】の問題と解説です。
大問が４問（昨年度は５問）と変わりましたが、
基本重視の問題構成は例年通りです。
偏りの少ないバランスの良い問題構成になっていますので、
過去問としての傾向を見るのも良いですが、
基本の定着確認をしておきましょう。

2022年（令和4年）度和歌山県公立高校入試【数学】の問題

令和４年度の和歌山県公立高校入試の数学の問題です。

⇒　２０２２年（令和４年）度の和歌山県公立高校入試【数学】の問題ＰＤＦ

和歌山県が公開してくれている問題をそのまま載せておきます。

2022年（令和4年）度和歌山県公立高校入試【数学】の解説

冒頭でも書いておきましたが、
問題構成は大問４問となりました。

ただし、これは傾向の変化とは言えないので例年通りと見ておきましょう。
内容的には基本重視で偏りの少ない、
取り組み方で差もしっかり出る問題となっています。

第１問

\(\color{black}{\fbox{\(\,\large{1}\,\)}}\)
式の計算、方程式、関数、図形と総合的な基本小問集合です。
〔問１〕
式の計算が(1)から(5)まであります。

(1)
　\(\hspace{10pt}-9+4\\
=\underline{　-5　}\)

正の数負の数の加減は数直線上で見るとわかりやすいです。
足し算は右に、引き算は左に移動します。

(2)
　\(\hspace{10pt}\displaystyle \frac{10}{3}+2\div \left(\,-\frac{3}{4}\,\right)\\
\displaystyle =\frac{10}{3}-2\times \frac{4}{3}\\
\displaystyle =\frac{10}{3}-\frac{8}{3}\\
\displaystyle =\underline{\underline{　\frac{2}{3}　}}\)

符号に注意して、
割り算を逆数の掛け算と処理すれば文字式でも同じです。

(3)
　\(\hspace{10pt}(3a+5b)+2(2a-b)\\
=3a+5b+4a-2b\\
=\underline{　7a+3b　}\)

ミスはもったいないので、
２行目はできるだけ暗算をさけたいところです。

(4)
　\(\hspace{10pt}\sqrt{48}-\sqrt{3}+\sqrt{12}\\
=4\sqrt{3}-\sqrt{3}+2\sqrt{3}\\
=\underline{　5\sqrt{3}　}\)

素因数分解を省略していますが、
たいした時間は必要としないので、
できるだけ暗算せずに確実に進めましょう。

(5)
　\(\hspace{10pt}(a+3)^2-(a+4)(a-4)\\
=(a^2+6a+9)-(a^2-16)\\
=a^2+6a+9-a^2+16\\
=\underline{　6a+25　}\)

２行目３行目は特に符号注意ですね。

〔問２〕
２次方程式を解きます。
　\(\begin{eqnarray}\displaystyle
x^2+5x-14&=&0\\
(x+7)(x-2)&=&0\\
x&=&\underline{　-7\,,\,2　}
\end{eqnarray}\)

方程式を解くことと解を求めることは同じです。

２次方程式を解くときは因数分解から試し、
因数分解できないときは解の公式です。

⇒　２次方程式を解の公式で解く問題の見分け方と例題

文章題では求めるものが整数であることが多いので、
因数分解は先に試すと良いですよ。

〔問３〕
全体が自然数となる自然数\(\,n\,\)を求めます。
　\(\hspace{10pt}\displaystyle \sqrt{\frac{20}{n}}\)

限られた範囲（\(\,1\,≦\,n\,≦\,20\,\)）になるので、
すべて試しても答えは出ますが、
全体が自然数になるのはルートの中が平方数である場合だけです。
　\(\hspace{10pt}20=2^2\times 5\)
であることから、
　\(\hspace{10pt}\displaystyle \frac{20}{n}=\frac{2^2\times 5}{n}\)

\(\,n=5\,\)のとき、
　\(\hspace{4pt}\displaystyle \sqrt{\frac{2^2\times \color{red}{5}}{\color{red}{5}}}=\sqrt{2^2}=2\,\)
全体が自然数になることは分かりますが、
\(\,n=2^2\times 5\,\)のときも、
　\(\hspace{4pt}\displaystyle \sqrt{\frac{2^2\times 5}{2^2\times 5}}=1\)
となり全体は自然数になることを見落とさないようにしましょう。

答え　\(\hspace{4pt}n=\underline{　5\,,\,20　}\)

⇒　ルートのついた無理数を整数や自然数に変える方法と問題の解き方

かけて平方数にする場合と割って平方数にする場合があります。
どちらも考え方は同じですね。

〔問４〕
関数の決定と代入問題です。

関数は反比例なので
　\(\hspace{4pt}\displaystyle y=\frac{a}{x}\)
とおけて\(\,x=5\,,\,y=4\,\)を満たすので比例定数\(\,a\,\)は
　\(\begin{eqnarray}\displaystyle
4&=&\frac{a}{5}\\
a&=&20
\end{eqnarray}\)
関数は
　\(\hspace{10pt}\displaystyle y=\frac{20}{x}\)

よって\(\,x=-10\,\)のとき
　\(\begin{eqnarray}\displaystyle
y&=&\frac{20}{-10}\\
&=&\underline{　-2　}
\end{eqnarray}\)

もちろん
　\(\hspace{10pt}x\,y=a\)
だから
　\(\hspace{10pt}a=5\times 4=20\)
としても良いです。

比例定数を求めず
　\(\hspace{10pt}\displaystyle 5\times 4=(-10)\times y\)
としても\(\,y\,\)の値を求める事はできますが、
関数を決定してからにしておきましょう。

〔問５〕
角度を求めます。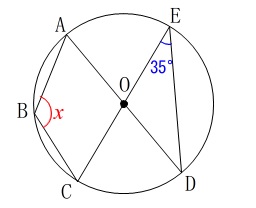分かる角度を次々と書き込んで行けば自ずと出ますが、
いくつか線分を足すと分かり易いです。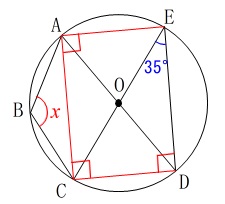線分\(\,\mathrm{AD}\,\)と\(\,\mathrm{CE}\,\)は直径なので、
　\(\hspace{10pt}\mathrm{∠ACD=∠CDE}=90^{\circ}\)
四角形\(\,\mathrm{ACDE}\,\)は長方形です。
（別に長方形という条件はなくても良いです。）
半径が等しいから二等辺三角形がたくさんありますね。

後は円周角の定理から出せるでしょう。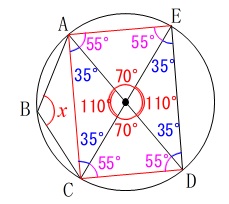すべて固定されて角度も決まっています。

\(\,∠x\,\)の中心角\(\,\mathrm{∠AOC=250°}\,\)なので
　\(\hspace{4pt}∠x=\underline{　125^{\circ}　}\)

中心角を小さい方と見てしまうと、
明らかに大きさが違うので気がつくでしょう。

〔問６〕
回転体の体積を求めます。

中心角９０°のおうぎ形なので、
回転体は半球になります。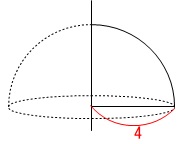球の半分なので求める体積\(\,V\,\)は
　\(\begin{eqnarray}\displaystyle
V&=&\frac{1}{2}\times \frac{4}{3}\,\pi\,(\,4\,)^3\\
&=&\underline{\underline{　\frac{128}{3}\,\pi　}}\,(\,\mathrm{cm^3}\,)
\end{eqnarray}\)

⇒　表面積や体積の求め方(三角柱,四角柱,円柱,球や半球)

球の体積を求める公式は、
中学生では求められないので覚えておくしかありません。

第２問

\(\color{black}{\fbox{\(\,\large{2}\,\)}}\)
確率、規則性、方程式、データの読み取り文章問題がいくとかあります。

〔問１〕
確率です。

「方法」は問題文から読み取って下さい。
簡単に説明すると
　\(\,\mathrm{A\,,\,B\,,\,C\,,\,D}\,\)の順番で玉を取り出し、
　取り出した数字の順に走る順番にする。

取り出し方をすべて樹形図にすれば答えは確実に出ますが、
少し説明しておきます。
（２４通りの取り出し方があることだけを確認しておいて下さい。）

第一走者が\(\,\mathrm{A}\,\)になるのは、
\(\,\mathrm{A}\,\)が「１」を取り出したときで、
第四走者が\(\,\mathrm{D}\,\)になるのは、
\(\,\mathrm{B\,,\,C}\,\)が「２」と「３」どちらかを取り出すときなので
（どちらが２、３でも構わない。）
　\(\begin{array}{|c|c|c|c|c|} \hline
\,\mathrm{A}\,&\,\mathrm{B} \,& \,\mathrm{C} \,& \,\mathrm{D} \,\\ \hline
\, 1\,& \,2\, & \,3\, &\,4\, \\ \hline
\,1\, & \,3\, & \,2\, & 4 \\ \hline
\end{array}\)
の二通りだけです。

よって、
　\(\hspace{4pt}\displaystyle \frac{2}{24}=\underline{\underline{　\frac{1}{12}　}}\)

確率の積を計算できるなら、
\(\,\mathrm{A}\,\)から順に玉を取り出すとして
\(\,\mathrm{A}\,\)が「１」、\(\,\mathrm{B}\,\)が「２」か「３」、\(\,\mathrm{C}\,\)が\(\,\mathrm{B}\,\)のあとの残りの「２」か「３」
（\(\,\mathrm{D}\,\)は必然的に「４」です。）
よって、
　\(\hspace{10pt}\displaystyle \frac{1}{4}\times \frac{2}{3}\times \frac{1}{2}=\frac{1}{12}\)
とすることもできますが、
樹形図で確実に取りに行きましょう。

〔問２〕
簡単な規則性の問題です。

図で見ると色もないからわかりにくいので、
表の方が規則性が見やすいです。
　\(\begin{array}{|c|c|c|c|c|c|c|c|c|c|} \hline
\,順番 \,& \color{blue}{1} & 2 & 3 & 4 & \color{red}{5} & \color{blue}{6} & 7 & 8 & 9 & \color{red}{10} & \color{blue}{11} & \cdots \\ \hline
色 & \color{blue}{青} & 黄 & 黒 & 緑 & \color{red}{赤} & \color{blue}{青} & 黄 & 黒 & 緑 & \color{red}{赤} & \color{blue}{青} & \cdots \\ \hline
\end{array}\)
赤は５の倍数なので周期が５と分かりました。
(1)
２７番目は「２５の次の次」なので、
答え　\(\hspace{4pt}\underline{　黄　}(\,色\,)\)
(2)
\(\,124\,\)番目は\(\,125\,\)番目の１つ前です。

１２５番目の赤が２５番目の赤でなので
　\(\hspace{4pt}\displaystyle \frac{125}{5}=25\)
１２４番目までに黒は
　\(\hspace{4pt}\underline{　25　}個\)

赤の前にある色は、赤と同じ数だけありますよね。
※
１２０番目の赤を考えても良いですよ。
そのときは１つ足すことを忘れないで下さい。

〔問３〕
方程式を立て、解く問題です。
連立方程式でも良いですが１次方程式で良いですね。

　「エビフライ弁当は唐揚げ弁当より５０円高い。」

基準が唐揚げ弁当なので唐揚げ弁当の定価を\(\,x\,\)とします。
　唐揚げ弁当１個\(\,x\,\)円
　エビフライ弁当１個\(\,(\,x+50\,)\,\)円

それぞれ２０個販売します。
エビフライ弁当は２０個\(\,(\,x+50\,)\,\)円で、
唐揚げ弁当は
　\(\,x\,\)円で１０個、
　５割引（半額）\(\displaystyle \frac{x}{2}\,x\,\)円で１０個販売、
売上合計が１５０００円なので
　\(\begin{eqnarray}\displaystyle
20(x+50)+10x+10\times \frac{x}{2}&=&15000\\
20x+1000+10x+5x&=&15000\\
35x&=&14000\\
x&=&400
\end{eqnarray}\)

答え　唐揚げ弁当　\(\,\underline{　400　}\,\)円　エビフライ弁当　\(\,\underline{　450　}\,\)円

連立方程式だと
　唐揚げ弁当１個\(\,x\,\)円
　エビフライ弁当１個\(\,y\,\)円
として
　\( \begin{cases}
\hspace{4pt} y=x+50\\
\hspace{4pt}\displaystyle 10x+10\times \frac{x}{2}+20y=15000
\end{cases}\)

となります。
※
比例計算（掛け算）の順序が逆になっている部分がありますが気にしなくて良いです。
そもそも、何の事か分からないでしょう？ｗ
普段なら
　「\(\,\color{red}{1}\,\)個\(\,\color{blue}{x}\,\)円、\(\,\color{red}{10}\,\)個販売」
の場合
　\(\hspace{4pt}\displaystyle \color{blue}{x}\times \frac{\color{red}{10}}{\color{red}{1}}\)
の回し方をします。

〔問４〕
箱ひげ図とヒストグラムの読み取りです。

読み取ってからだと時間がかかりすぎるので、
問題に合わせて進めて行きます。
(1)
（\(\,\mathrm{Ⅰ}\,\)）
四分位範囲は
　\((第３四分位数)-(第１四分位数)\)
なので箱の横幅が大きさになります。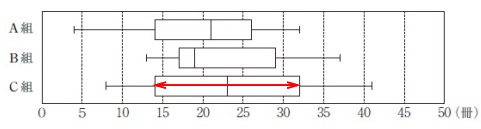一番大きいのは\(\,\mathrm{C}\,\)組です。

正しくない。\(\,\underline{　イ　}\,\)

（\(\,\mathrm{Ⅱ}\,\)）
中央値で分けるとおおよそ全体の半数となるので、
クラスの人数から考えれば良いです。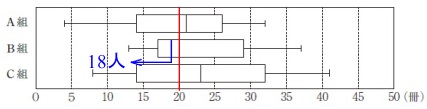\(\,20\,\)冊以下人数は、
中央値が\(\,20\,\)より小さい\(\,\mathrm{B}\,\)組が少なくとも\(\,18\,\)人はいるので正しい。
　\(\hspace{4pt}\underline{　ア　}\)

（\(\,\mathrm{Ⅲ}\,\)）
各四分位数になるのが何人目になるのか考えれば分かります。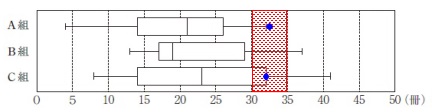\(\,\mathrm{A}\,\)組は最大値となる人が必ずいます。
\(\,\mathrm{C}\,\)組は第３四分位数になる人が必ずいます。
しかし、\(\,\mathrm{B}\,\)組はいるかもしれませんが、
２９冊、または３７冊借りた人がたくさんいた場合でも
同じ箱ひげ図になるので必ずではありません。
　\(\hspace{4pt}\underline{　ウ　}\)

(2)
Ｃ組の箱ひげ図となるヒストグラムを選びます。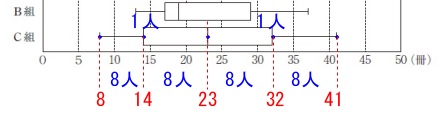ざっくりですが人数は四分位範囲で分けることができるので、
最小値、中央値、最大値を見ていくと絞れます。

最小値が\(\,8\,\)、最大値が\(\,41\,\)なのでエは違います。
箱ひげ図の中央値が\(\,23\,\)なのでアのヒストグラムは中央値が違います。
（小さい方から\(\,17\,\)人目\(\,18\,\)人目の平均になるから(17.5)）

これでイかウに絞れました。
次に第１四分位数を見ると１５冊以下の人は９人はいるはずなので、
答え　\(\,\underline{　ウ　}\,\)

ここでは四分位数などの用語の説明をしておりませんが、
データ（資料）については用語の意味が分からないと問題を解くことができません。

逆に用語の意味さえしっかり押さえておけば、
少しの作業で答えが出せます。

⇒　代表値とは？度数分布表の平均値,中央値の求め方と最頻値の答え方

代表値などはこれからも必要になりますよ。

(3)
標本調査についてです。

すべてを調べる事が難しいときに代表的に選んで推測するのが、
標本調査なので「無作為」に選ばなくてはいけません。
（限定的な条件はつけてはならない。）

３年生だけに限定するのは適切ではありません。

解答としては「無作為」という用語が含まれていれば何でも良いです。
（「３年生だけ」という事が限定的であるという意味で使っていればです。）

第３問

\(\color{black}{\fbox{\(\,\large{3}\,\)}}\)
関数です。
全体に与えられている条件は
　\(\hspace{4pt}\displaystyle y=\frac{1}{4}\,x^2　･･･①\)
　点\(\,\mathrm{A\,(\,-2\,,\,1\,)}\,\)
で変わらないので忘れないようにしましょう。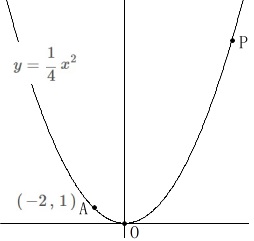
〔問１〕
変化の割合を求めます。
\(\hspace{10pt}\displaystyle (\,変化の割合\,)=\frac{　(\,y\,の増加量\,)　}{　(\,x\,の増加量\,)　}\)

　\(\hspace{4pt}x:-2\,\rightarrow 0\)
このとき\(\,y\,\)の値は
　\(\hspace{4pt}y:1\,\rightarrow 0\)
となるので変化の割合は
　\(\hspace{4pt}\displaystyle \frac{0-1}{0-(-2)}=\underline{\underline{　-\frac{1}{2}　}}\)

変化の割合は直線の傾きでもありますよ。

〔問２〕
変域問題です。
グラフを見ていけばおおよその見当はつきますし、
グラフが適当であれば直感的でも間違いありません。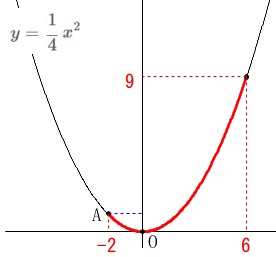\(\,y\,\)の変域は\(\,0\,\)以上で、
最大値\(\,9\,\)となるのは\(\,x=6\,\)のときしかありません。

答え　ア　\(\,\underline{　6　}\,\)　イ　\(\,\underline{　0　}\,\)

計算を省略していますが\(\,y=9\,\)となる\(\,x\,\)は
　\(\begin{eqnarray}\displaystyle
9&=&\frac{1}{4}\,x^2\\
36&=&x^2
\end{eqnarray}\)
を解いて\(\,-2\,\)以上の\(\,x\,\)を求めています。

〔問３〕
条件は\(\,\mathrm{△OPB}\,\)が二等辺三角形になることです。
\(\,\mathrm{P}\,\)は\(\,①\,\)上の点での\(\,x\,\)座標が\(\,-4\,\)なので
　\(\hspace{10pt}\mathrm{P}\,(\,-4\,,\,4\,)\)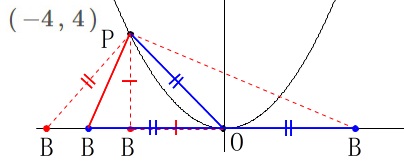２点\(\,\mathrm{O\,,\,P}\,\)は固定されていますが４通りあります。
わかりにくいかもしれないので少し説明を加えておきます。
　\(\hspace{10pt}\mathrm{PB=PO}\)
　\(\hspace{10pt}\mathrm{PB=BO}\)
　\(\hspace{10pt}\mathrm{PO=OB}\)（二通り）
の４通りです。

\(\,\mathrm{P}\,\)の座標から\(\,\mathrm{OP=\color{blue}{4\sqrt{2}}}\,\)なので、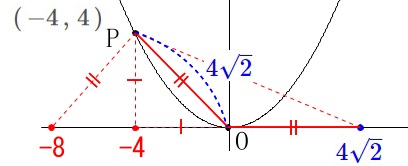\(\,x\,\)座標が最も大きくなるのは\(\,\mathrm{PO=OB}\)のときで、
（\(\,x\,\)座標が大きい方の）
　\(\hspace{10pt}\mathrm{B}\,\underline{　(\,4\sqrt{2}\,,\,0\,)　}\)
\(\,x\,\)座標が最も小さくなるのは\(\,\mathrm{PB=PO}\)のときで
　\(\hspace{10pt}\mathrm{B}\,\underline{　(\,-8\,,\,0\,)　}\)

座標上で二等辺三角形を見ているので、
わかりにくいかもしれませんがじっくり見ておいて下さい。

〔問４〕
四角形の面積を２等分する直線の式を求めますが、
条件があるので座標上で確認しておきましょう。
　点\(\,\mathrm{C\,(\,4\,,\,4\,)}\,\)
　\(\,\mathrm{△OPD:△ODC=3:2}\,\)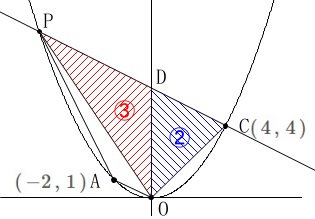底辺を\(\,\mathrm{OD}\,\)と見ると、
面積比は\(\,x\,\)座標の差を比とすることができるので、
点\(\,\mathrm{P}\,\)の\(\,x\,\)座標は\(\,-6\,\)なので
　点\(\,\mathrm{P\,(\,-6\,,\,9\,)}\,\)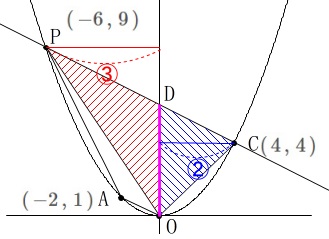このとき、
\(\,\mathrm{A}\,\)を通り四角形\(\,\mathrm{OAPC}\,\)の面積を２等分する直線を求めます。

\(\,\mathrm{P}\,\)は固定されたのでどうとでもなりそうですが、
大まかに方針は３つあります。

一つ目は、（おすすめできませんが）
「分からない！答えだけでも書いておくか」、ということで
なんとなく点\(\,\mathrm{D}\,\)を通るときと決めつけて、
直線\(\,\mathrm{PC}\,\)の式を先ずは求めます。
　\(\hspace{10pt}\displaystyle y=-\frac{1}{2}\,x+6\)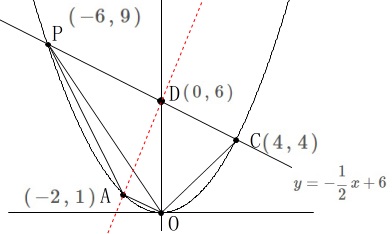点\(\,\mathrm{D}\,(\,0\,,\,6\,)\,\)が切片なので
２点\(\,\mathrm{A\,,\,D}\,\)を通る直線が　
　\(\hspace{10pt}\displaystyle \underline{\underline{　y=\frac{5}{2}\,x+6　}}\)
これは何の根拠もありません。
単なる解答欄の穴埋めです。
ただし、おおよその検討をつける目的で試して見たらたまたま２等分していた、
ということであれば答えにして大丈夫です。

次に、問題の流れを気にせず、
四角形\(\,\mathrm{OAPC}\,\)の面積\(\,S\,\)を求め、
　\(\hspace{10pt}S=\color{red}{36}\)
（頂点が固定されているので具体的に求まります。）
直線\(\,\mathrm{PC}\,\)上の点\(\,\mathrm{Q}\,\)を座標設定して、
\(\,\mathrm{△PAQ}\,\)の面積が\(\,\color{red}{36}\,\)の半分\(\,\color{blue}{18}\,\)になるように\(\,\mathrm{Q}\,\)を定め、
直線\(\,\mathrm{AQ}\,\)の式を求める方法です。

これは会員でも公式カードを使いこなせるようになっていないと、
説明が長くなるので解説しません。ｗ
それでも具体的な面積\(\,36\,\)が出ていれば、
\(\,\mathrm{△ODC}\,\)の面積が\(\,12\,\)なので\(\,\mathrm{△OAD}\,\)が\(\,6\,\)だから、
直線\(\,\mathrm{AD}\,\)が２等分するということはすぐに気がつくと思いますけど。

ここでは問題の意図と思われる、（推測です。）
台形の面積を等分する解説だけにしておきます。

直線\(\,\mathrm{AO}\,\)は
　\(\hspace{10pt}\displaystyle y=-\frac{1}{2}\,x\)
で直線\(\,\mathrm{PC}\,\)と平行です。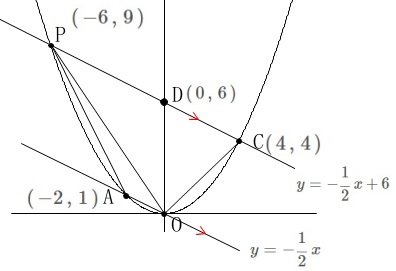このとき四角形\(\,\mathrm{OAPC}\,\)は台形です。

ここからも方針は分かれそうですが、
長さを比で表して進めます。

\(\,x\,\)座標の差から
　\(\hspace{4pt}\displaystyle \mathrm{OA:CP}=\color{red}{2}:\color{red}{10}\)
（具体的な長さでも\(\,1:5\,\)でも良いですよ。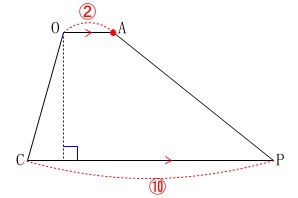）さて、点\(\,\mathrm{A}\,\)を通り２等分するにはどうしましょう。

図形的に考えるより、
高さを文字\(\,\color{blue}{h}\,\)でおいて（具体的な高さも求めようと思えば求まりますが）
機械的に解決できるように底辺を分割します。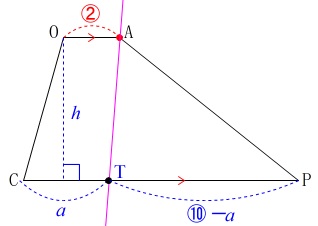比を長さとみて\(\,\mathrm{CP}\,\)を
　\(\hspace{4pt}\mathrm{CT:TP}=a:10-a\)
のとき２等分するとします。
（\(\,a:b\,\)でもいいですが、\(\,a+b=10\,\)なので省略しました。）

このとき台形\(\,\mathrm{OATC}\,\)と\(\,\mathrm{△ATP}\,\)の面積が等しくなるので
　\(\begin{eqnarray}
(\,台形\,\mathrm{OATC}\,)&=&\mathrm{△ATP}\\
\frac{2+a}{2}\times \color{blue}{h}&=&\frac{1}{2}\times (10-a)\times \color{blue}{h}\\
\frac{2+a}{2}&=&\frac{1}{2}\times (10-a)\\
2+a&=&10-a\\
2a&=&8\\
a&=&4
\end{eqnarray}\)

つまり
　\(\hspace{4pt}\mathrm{CT:TP}=4:6\)
になるとき２等分します。
（\(\,2:3\,\)でも良いですが\(\,x\,\)座標で見やすくしています。）

\(\,x\,\)座標で考えると\(\,\mathrm{T}\,\)は\(\,y\,\)軸上の点になるので、
点\(\,\mathrm{A}\,\)と点\(\,\mathrm{D}\,\)を通る直線が四角形を２等分すると分かりました。よって、
２点
　\(\mathrm{A}\,(\,-2\,,\,1\,)\,\)
　\(\mathrm{D}\,(\,0\,,\,6\,)\,\)
を通る直線が四角形\(\,\mathrm{OAPC}\,\)を２等分するので
　\(\hspace{4pt}\displaystyle \underline{\underline{　y=\frac{5}{2}\,x+6　}}\)

⇒　変化の割合とは？1次関数の求め方と直線の方程式との違い

直線の式は１問の中でも何度も求める事になりますので、
できるだけ短時間で求められるようになっておいた方が良いですよ。
（途中過程でも直線の式を求めない入試問題は考えられない。）

他にもいろいろと方法を用意された問題です。
ここでは台形の分割の考えかただけでも見ておいて下さい。

第４問

\(\color{black}{\fbox{\(\,\large{4}\,\)}}\)
平面図形です。

全体を通じてある条件は
　１辺\(\,\mathrm{6\,cm}\,\)の正方形です。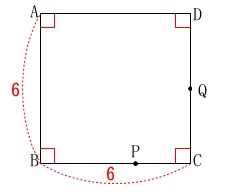後は問題によって変わりますので順に見ていきます。

〔問１〕
角度と面積を求めます。
条件
　\(\hspace{4pt}\mathrm{∠APB}=\color{red}{60°}\,,\,\mathrm{∠AQD}=\color{blue}{70°}\)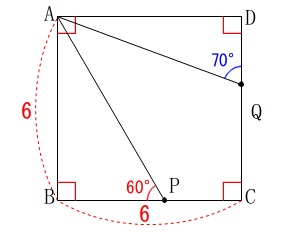
(1)
先ずは角度です。
\(\,\mathrm{∠PAQ}\,\)を求めます。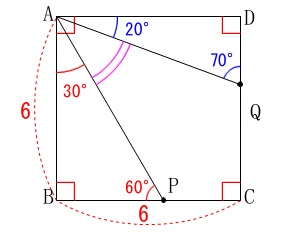三角形の内角の和から求めれば良いでしょう。
　\(\begin{eqnarray}\mathrm{∠PAQ}&=&90°-(\color{red}{30°}+\color{blue}{20°})\\
&=&\underline{　40^{\circ}　}
\end{eqnarray}\)

四角形\(\,\mathrm{APCQ}\,\)の内角からでも良いですよ。
分かる角度を次々に書き込んでいけばすべての角度が固定されています。

(2)
次は面積です。
\(\,\mathrm{△ABP}\,\)の面積を求めます。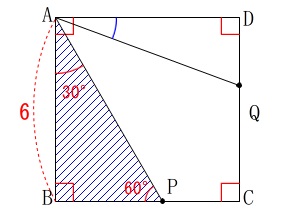\(\,\mathrm{△ABP}\,\)は三角定規なので
　\(\begin{eqnarray}\displaystyle
\mathrm{BP:AB}&=&\color{red}{1}:\color{red}{\sqrt{3}}\\
\mathrm{BP}:6&=&1:\sqrt{3}\\
\sqrt{3}\times \mathrm{BP}&=&6\\
\mathrm{BP}&=&\frac{6}{\sqrt{3}}\\
&=&\color{blue}{2\sqrt{3}}
\end{eqnarray}\)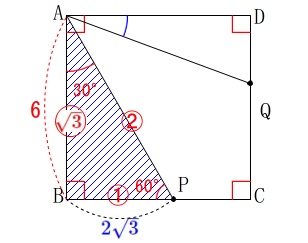よって、
　\(\begin{eqnarray}\displaystyle
\mathrm{△ABP}&=&\frac{1}{2}\times \mathrm{BP}\times \mathrm{AB}\\
&=&\frac{1}{2}\times \color{blue}{2\sqrt{3}}\times \color{red}{6}\\
&=&\underline{　6\sqrt{3}　}\,(\,\mathrm{cm^2}\,)
\end{eqnarray}\)

〔問２〕
証明です。
条件
　\(\,\mathrm{BP=CQ}\,\)
（問題全体の正方形の条件は変わっていませんよ。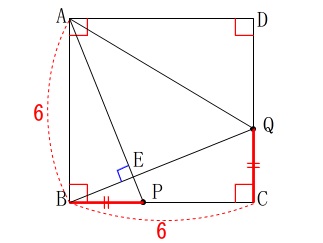）このとき
　\(\hspace{4pt}\mathrm{∠AEB}=90°\)
を証明します。

合同か相似か？
両方使いましょう。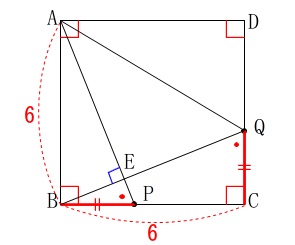条件
　\(\,\mathrm{BP=CQ}\,\)
から\(\,\mathrm{△ABP}\,\)と\(\,\mathrm{△BCQ}\,\)において
正方形という条件があるので
　\(\,\mathrm{AB=BC}\,,\,\mathrm{∠ABP=∠BCQ}=90^{\circ}\)
と合わせて合同条件
　「二組の辺とその間の角が等しい。」
がそろうので合同が言えます。

このとき\(\,\mathrm{△BPE}\,\)と\(\,\mathrm{△BQC}\,\)は、
\(\,\mathrm{∠PBE=∠QBC}\,\)を共通としていて
「二組の角がそれぞれ等しい。」
と相似条件がそろうので
　\(\,\mathrm{△BPE}\,\)∽\(\,\mathrm{△BQC}\,\)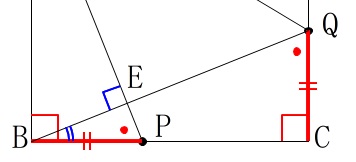
よって、
　\(\hspace{4pt}\mathrm{∠BEP=∠AEP}=90^{\circ}\)

証明の書き方はお任せします。

⇒　中学の図形証明問題(合同･相似)の解き方と証明の書き方ポイント

三角形の内角の和を利用しても良いですが、
合同と相似の両方の証明で示しておきました。

〔問３〕
３点\(\,\mathrm{A\,,\,P\,,\,Q}\,\)を通る円の半径を求めます。
条件
　\(\,\mathrm{BP=PC\,,\,∠BAP=∠CPQ}\,\)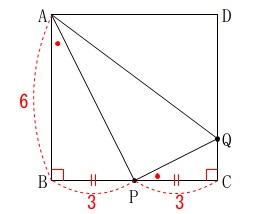正方形の条件は変わっていません。

証明の必要はないでしょう。
　\(\,\mathrm{△ABP}\,\)∽\(\,\mathrm{△PCQ}\,\)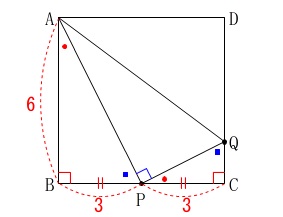なので三角形の内角の和から
　\(\hspace{4pt}\mathrm{∠APQ}=90^{\circ}\)

これは線分\(\,\mathrm{AQ}\,\)が、
３点\(\,\mathrm{A\,,\,P\,,\,Q}\,\)を通る円の直径となっていることを示しています。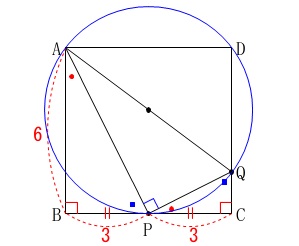つまり、
求める円の半径は線分\(\,\mathrm{AQ}\,\)の半分の長さです。

線分\(\,\mathrm{AQ}\,\)の長さを求めましょう。

点\(\,\mathrm{P}\,\)は\(\,\mathrm{BC}\,\)の中点なので
　\(\hspace{4pt}\mathrm{BP=PC}=\color{red}{3}\)

ここから\(\,\mathrm{AQ}\,\)の長さを求める方向を２つやっておきます。
どちらも三平方の定理利用なのでどちらでも良いです。

①三平方の定理から（\(\,\mathrm{△APQ}\,\)に適用します。）
　\(\hspace{4pt}\mathrm{AP}=\color{blue}{3\sqrt{5}}\)
\(\,\mathrm{△ABP}\,\)∽\(\,\mathrm{△PCQ}\,\)で相似比\(\,2：1\,\)から　
　\(\hspace{4pt}\displaystyle \mathrm{PQ}=\color{blue}{\frac{3\sqrt{5}}{2}}\)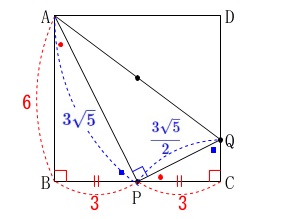さらに三平方の定理から
　\(\begin{eqnarray}
\mathrm{AQ^2}&=&\mathrm{AP^2+PQ^2}\\
&=&(\color{blue}{3\sqrt{5}})^2+\left(\color{blue}{\frac{3\sqrt{5}}{2}}\right)^2\\
&=&45+\frac{45}{4}\\
&=&\frac{225}{4}\\
\mathrm{AQ}&=&\pm \frac{15}{2}
\end{eqnarray}\)
長さなので\(\,\mathrm{AQ\,＞\,0}\,\)だから
　\(\hspace{4pt}\displaystyle \mathrm{AQ}=\frac{15}{2}\)

よって求める半径は
　\(\hspace{10pt}\displaystyle \underline{\underline{　\frac{15}{4}　}}\)

②\(\,\mathrm{△ABP}\,\)∽\(\,\mathrm{△PCQ}\,\)で相似比\(\,2：1\,\)から
　\(\hspace{10pt}\displaystyle \mathrm{CQ}=\color{blue}{\frac{3}{2}}\)
このとき\(\,\mathrm{DQ=DC-CQ}\,\)なので
　\(\hspace{10pt}\displaystyle \mathrm{DQ}=\color{magenta}{\frac{9}{2}}\)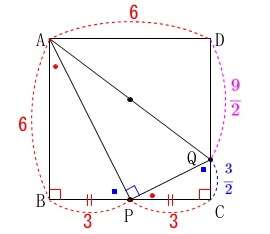三平方の定理から（\(\,\mathrm{△ADQ}\,\)に適用します。）
　\(\begin{eqnarray}\displaystyle
\mathrm{AQ^2}&=&\mathrm{AD^2+DQ^2}\\
&=&\color{red}{6}^2+\left(\,\color{magenta}{\frac{9}{2}}\,\right)^2\\
&=&36+\frac{81}{4}\\
&=&\frac{225}{4}
\end{eqnarray}\)
\(\,\mathrm{AQ\,＞\,0}\,\)だから
　\(\hspace{10pt}\displaystyle \mathrm{AQ}=\frac{15}{2}\)
よって、求める半径は
　\(\hspace{10pt}\displaystyle \underline{\underline{　\frac{15}{4}　}}\)

どちらでも良いので思いついた方向で突っ走った方が早いです。

以上です。

どれも解法や方向性が１つとは決められていません。
ここで示した解法の他にもいろいろとあります。
割と自由度のある問題なので、
基本をしっかり抑えて、
自分で手を動かせばある程度は見えて来ますよ。

⇒　和歌山県公立高校入試の数学の過去問題と解答解説

過去数年分見てくと傾向は見えてきます。
対策はお任せしますが、
応用に時間をかけるよりも基本の繰り返しの方が重要です。