２０２３年(令和５年)度青森県公立高校入試の数学問題と解説です。
問題の構成と難易度に大きな変化はありません。
第５問の整数問題でもそれ程差がつくとは思えないので、
ミスに注意して基本通りの試験の受け方をしていれば問題ないでしょう。
数学を苦手にしている人は例年の配点を見て対策すると良いですよ。
2023年(令和5年)度青森県公立高校入試【数学】の問題
問題は大問５つです。
⇒ 2023年(令和5年)度秋田県公立高校入試の数学の問題ＰＤＦ
注意書きは例年大きくは変わらないので受験生は読んでおくと良いです。
2023年(令和5年)度青森県公立高校入試【数学】の解説
問題の表紙に書いてある通り試験は４５分です。
数学を苦手にしている人にとっては十分過ぎる時間とはいえないでしょう。
用語はもちろんですが試験の受け方の基本も抑えて取り組むと良いです。
対策ページではないのでさっさと解説していきます。
第１問
\(\color{black}{\large{\fbox{1}}}\)
第１問は基本の小問集合です。
(1)
ア
正の数負の数の計算です。
\(\hspace{10pt}4-10\\
=\underline{ -6 }\)
引き算では数直線上で左に移動します。
⇒ 正の数負の数の加法減法と分数計算問題でミスを減らすポイント
ミスしたくないところですが、
うっかりすることは皆あるので確実に取りましょう。
イ
もう一度正の数負の数の計算です。
\(\hspace{10pt}(-2)^2\times 3+(-15)\div (-5)\\
=4\times 3+3\\
=12+3=\underline{ 15 }\)
暗算でもできる計算部分はあると思いますが符号には注意しておきましょう。
⇒ 正の数負の数の計算で加減乗除の混じった計算のポイントと練習問題
ウ
文字式の引き算です。
連立方程式の処理で慣れていると思いますが、
引く文字式は全体なので符号に注意しましょう。
\(\hspace{20pt}6x^2-x-5\\
\underline{ -)2x^2+x-6 }\\
\hspace{20pt}4x^2-2x+1\)
普通に文字式として計算すると
\(\hspace{10pt}(6x^2-x-5)-(2x^2+x-6)\\
=6x^2-x-5-2x^2-x+6\\
=\underline{ 4x^2-2x+1 }\)
ということですので検算でもしておくと良いですね。
エ
今度は文字式の割り算です。
\(\hspace{10pt}\displaystyle (6x^2y+4xy^2)\div 2xy\\
=\underline{ 3x+2y }\)
これは係数が割り切れるので暗算でも良いですが、
ややこしいときは分数として処理するといつも上手くいきます。
\(\hspace{10pt}\displaystyle (6x^2y+4xy^2)\div 2xy\\
\displaystyle =\frac{6x^2y+4xy^2}{2xy}\\
\displaystyle =\frac{6x^2y}{2xy}+\frac{4xy^2}{2xy}\\
=3x+2y\)
暗算でも良い部分はありますがミスの無いよう確実に取りましょう。
ていねいにやりすぎても時間がかかるので見直しのときでも良いです。
オ
無理数の計算です。
\(\hspace{10pt}\displaystyle \sqrt{\frac{3}{2}}-\frac{\sqrt{54}}{2}\\
\displaystyle =\frac{\sqrt{3}\times \sqrt{2}}{\sqrt{2}\times \sqrt{2}}-\frac{\sqrt{54}}{2}\\
\displaystyle =\frac{\sqrt{6}-3\sqrt{6}}{2}\\
\displaystyle =-\frac{2\sqrt{6}}{2}=\underline{\underline{ -\sqrt{6} }}\)
分母の有理化は慣れていれば暗算でも良いですが、
不安があればていねいにやった方が良いですよ。
分数計算は分母を１つに（通分）して分子の計算に集中するのはいつも通りです。
(2)
文字式の意味を考えます。
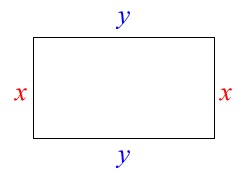問題に「長方形」などの図形を表す言葉を見たら図は書くと良いです。
縦が\(\,\color{red}{x}\,\)、横が\(\,\color{blue}{y}\,\)なので、
\(\hspace{4pt}2(x+y)\,\)は長方形の「周の長さ」を意味しています。
(3)
相対度数と累積相対度数を求めます。
相対度数は全体に対するその階級の割合、
\(\hspace{4pt}\displaystyle ( 相対度数 )=\frac{ (\,階級の度数\,) }{ (\,度数合計\,) }\)
累積相対度数は小さい方からその階級までの相対度数の和になります。
\(\begin{array}{|c|c|c|} \hline
階級 & 度数 & 相対度数 \\ \hline
16～20 & 4 & 0.20 \\ \hline
20～24 & 6 & \color{red}{0.30} \\ \hline
24～28 & 1 & 0.05 \\ \hline
28～32 & 7 & 0.35 \\ \hline
32～36 & 2 & 0.10 \\ \hline
合計 & 20 & 1.00 \\ \hline
\end{array}\)
\(\,\mathrm{20\,m}\,\)以上\(\,\mathrm{24\,m}\,\)未満の階級の相対度数は
\(\hspace{10pt}\underline{ 0.30 } または \underline{ 0.3 }\)
この階級だけを見れば割り切れるので\(\,0.3\,\)とした人も多いでしょう。
ただ、累積を考えると迷ったかもしれません。
\(\,\mathrm{28\,m}\,\)未満の累積相対度数は表の上から３番目までの和になるので
\(\hspace{4pt}0.20+0.30+0.05=\underline{ 0.55 }\)
用語の意味を理解していれば問題ないでしょう。
⇒ 度数分布表とは？階級の幅と階級値および累積度数とヒストグラム
相対度数や累積相対度数についても加筆しているので見ておくと良いです。
(4)
因数分解です。
因数分解の手順は決まっているので説明は傾きます。
\(\hspace{10pt}3x^2-6x-45\\
=3(x^2-2x-15)\\
=\underline{ 3(x+3)(x-5) }\)
めったにない特殊なケース以外は複雑な因数分解でも基本手順は同じです。
（特殊なのは高校以上でかなりやっかいな部類の因数分解です。）
(5)
１次関数の傾きと切片（\(\,y\,\)切片）を求めます。
\(\hspace{10pt}y=ax+b\)
傾きから求めましょう。
「\(\,x\,\)の値が\(\,\color{red}{2}\,\)増加すると\(\,y\,\)の値が\(\,\color{blue}{4}\,\)増加する。」
\(\begin{eqnarray}
a&=&\frac{\color{blue}{4}}{\color{red}{2}}\\
&=&\underline{ 2 }
\end{eqnarray}\)
傾きが分かったので元の関数は
\(\hspace{10pt}y=2x+b\)
となり、\(\,x=1\,\)のとき\(\,y=-3\,\)である条件から
\(\begin{eqnarray}
-3&=&2(1)+b\\
b&=&\underline{ -5 }
\end{eqnarray}\)
１次関数は直線なので２点を通る条件から求める練習をしておけば良いです。
ていうか、何度もしておいた方が良いです。
(6)
角度を求める問題です。
平行線があるので同位角、錯角から分かる角度を書き込んで行けば良いですね。
\(\begin{eqnarray}
25°+∠x&=&72°\\
∠x&=&72°-25°\\
&=&\underline{ 47° }
\end{eqnarray}\)
求め方は「三角形の内角の和が\(\,180°\,\)」からでも良いです。
(7)
四角形の１辺の長さを求めます。
\(\,75°\,\)の使い道は直角二等辺三角形を作れば良いことを条件が教えてくれています。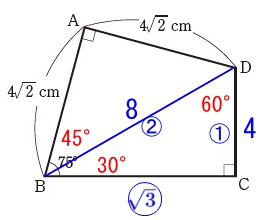
三角定規が2つくっついた形なので比例式で良いです。
先ずは直角二等辺三角形から\(\,\mathrm{BD}\,\)を求めておきます。
\(\begin{eqnarray}
\mathrm{AB:BD}&=&1:\sqrt{2}\\
4\sqrt{2}:\mathrm{BD}&=&1:\sqrt{2}\\
\mathrm{BD}&=&\color{blue}{8}
\end{eqnarray}\)
\(\,\mathrm{BD}\,\)からでも良いですが\(\,\mathrm{DC=4}\,\)はすぐに分かるので計算が楽です。
\(\begin{eqnarray}
\mathrm{DC:BC}&=&1:\sqrt{3}\\
4:\mathrm{BC}&=&1:\sqrt{3}\\
\mathrm{BC}&=&\underline{ 4\sqrt{3} (\,\mathrm{cm}\,)}
\end{eqnarray}\)
気づくとか、慣れとか言う前に対角線を引いてみる、
という基本的な作業からですね。
(8)
箱ひげ図が表す意味です。
適切でないものを１つ選ぶので、
微妙なものよりより明らかに違う違うものを探しましょう。
答え \(\,\underline{ ウ }\,\)
範囲（レンジ）は最大値から最小値を引いたものです。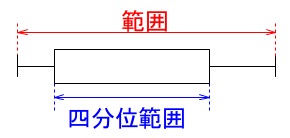
箱の長さは四分位範囲です。
第１問はここまでです。
基本ばかりですがここまでの配点は確認しておきましょう。
第２問
\(\large{\color{black}{\fbox{2}}}\)
(1)
\(\,90°\,\)回転の作図です。
垂線が引ければ問題ありませんが、
線分を直線にする、２点を結ぶ、なども作図のひとつですから忘れないようにしましょう。
垂線を先に引いて円を書く（回転）、という手順でも良いです。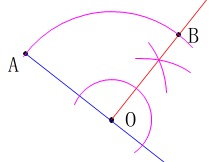
半径をいろいろ変えるのが手間ですけどね。
間違ってはいないのでどっちでも良いです。
(2)
５枚のカードから３枚取り出してできる３桁の整数です。
\(\color{black}{\fbox{1}}\) \(\color{black}{\fbox{2}}\) \(\color{black}{\fbox{3}}\) \(\color{black}{\fbox{4}}\) \(\color{black}{\fbox{5}}\)
［問題］は「３５０以上になる確率を求めなさい。」、です。
確率の問題ですので樹形図を書き出せば確実にとれます。
難しくはありませんが時間との闘いになるかもしれませんね。
１枚ずつ続けて３回取り出すので取り出したカードは戻していません。
「例えば」とあるので３桁の整数がどうやってできるか見ておきましょう。
１回目に取り出したカードは百の位、
２回目に取り出したカードは十の位、
３回目に取り出したカードは一の位になります。
１回目に\(\,\color{red}{1}\,\)のとき、
\(\hspace{10pt}\color{red}{1}\,\color{blue}{○}\,\color{magenta}{○}\)
となります。
続いて２回目に\(\,\color{blue}{2}\,\)のとき、
\(\hspace{10pt}\color{red}{1}\,\color{blue}{2}\,\color{magenta}{○}\)
さらに３回目に\(\,\color{magenta}{3}\,\)のとき、
\(\hspace{10pt}\color{red}{1}\,\color{blue}{2}\,\color{magenta}{3}\)
と整数ができます。
１回目に\(\,\color{red}{1}\,\)のときだけでも樹形図を書いてみると良いですが、
\(\,\color{blue}{2}\,\)回目\(\,\color{magenta}{3}\,\)回目の数によって\(\,12\,\)通りの整数ができます。
１回目は\(\,1\,\)を取り出し、残りは４つ。
\(\color{black}{\fbox{2}}\) \(\color{black}{\fbox{3}}\) \(\color{black}{\fbox{4}}\) \(\color{black}{\fbox{5}}\)
２回目で残りの４つから１つ、
３回目は１回目２回目で取り出していない３つの中から選ぶことになるからです。
\(\hspace{10pt}4\times 3\,=\,12\)
百の位は\(\,1\,\)とは限らず５つあるので３桁の整数はその５倍できるので
\(\hspace{10pt}5\times 4\times 3=\underline{ 60 }\,\)通り。
百の位が\(\,1\,\)と\(\,2\,\)のときは［問題］の条件を満たさないので
百の位に着目して考えてみよう、ということで\(\color{black}{\fbox{\(\,\mathrm{X}\,\)}}\)には百が入ります。
\(\color{black}{\fbox{\(\,\mathrm{X}\,\)}}\) \(\,\underline{ 百 }\,\)
百の位が\(\,3\,\)で条件を満たすのは十の位が\(\,5\,\)のときだけなので、
一の位には残りの\(\,1\,,\,2\,,\,4\,\)の\(\,\underline{ 3 }\,\)通りがあります。
百の位が\(\,\underline{ 4 }\,,\,\underline{ 5 }\,\)のときはすべて条件を満たします。
百の位が\(\,4\,\)のとき十の位一の位は何でも良いので残りの枚数から
\(\hspace{10pt}4\times 3\,=\,12\)
百の位が\(\,5\,\)のときも同じく\(\,12\,\)通りあるので、
問題の条件を満たす\(\,350\,\)以上の整数は全部で
\(\hspace{10pt}3+12+12\,=\,27\,\)通り。
よって求める確率は
\(\hspace{10pt}\displaystyle \frac{27}{60}=\underline{\underline{ \frac{9}{20} }}\)
樹形図を書いていくうちに全部で\(\,60\,\)通りになることに気がつけば、
大きい方から書き出して数えればそれ程時間はかかりませんよ。
説明が長いですが実際には短時間で答えは出ていると思います。
樹形図を書き出してもそれ程時間はかかりませんから。
問\(\,\large{ア}\,\)に入れる数や位を読み取れば問題ないでしょう。
第３問
\(\large{\color{black}{\fbox{3}}}\)
正方形の図形問題ですが基本的なので簡単に済ませます。
(1)
長さと体積を求めます。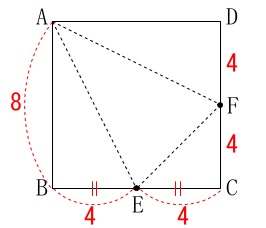
中点\(\,\mathrm{E\,,\,F}\,\)から分かる長さを書き込んであります。
ア
線分\(\,\mathrm{AE}\,\)は直角三角形の斜辺なので三平方の定理から
\(\begin{eqnarray}
\mathrm{AE^2}&=&\mathrm{AB^2+BE^2}\\
&=&8^2+4^2\\
&=&80\\
\mathrm{AE}&=&\pm 4\sqrt{5}
\end{eqnarray}\)
長さなので
\(\hspace{10pt}\mathrm{AE}=\underline{ 4\sqrt{5} }(\mathrm{cm})\)
イ
三角錐を作ったとき\(\,\mathrm{B\,,\,D}\,\)が\(\,\mathrm{C}\,\)に重なることから、
底面を\(\,\mathrm{△CFE}\,\)と見ると高さは\(\,\mathrm{AB}\,\)になります。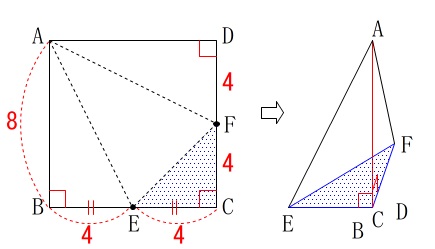
面に垂直である直線は、
平面上のどの線分とも垂直になるので逆に\(\,\mathrm{AB}\,\)が高さとなることは分かりますね。
（ア）
三角錐の体積\(\,V\,\)は底面が直角二等辺三角形\(\,\mathrm{CFE}\,\)なので
\(\begin{eqnarray}
V&=&\frac{1}{3}\times \color{blue}{\mathrm{△CFE}}\times \color{red}{\mathrm{AB}}\\
&=&\frac{1}{3}\times \color{blue}{\frac{1}{2}\times 4\times 4}\times \color{red}{8}\\
&=&\underline{\underline{ \frac{64}{3} }}(\mathrm{cm^3})
\end{eqnarray}\)
（イ）
（ア）とは底面を変えてみますので三角錐を転がします。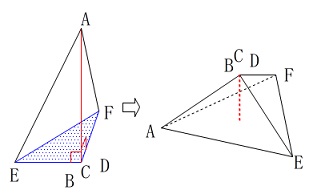
このとき体積\(\,V\,\)は変わらないことに注目です。
底面の\(\,\mathrm{△AEF}\,\)の面積は二等辺三角形なので、
垂線を引いて自分で求めておけるようにして下さい。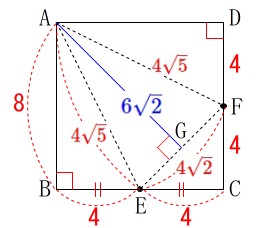
この段階ができないとこの手の問題は解けません。
ということで少し説明を省略しますが、
求める高さを\(\,\color{red}{h}\,\)とすると
\(\begin{eqnarray}
V&=&\frac{1}{3}\times \color{magenta}{\mathrm{△AEF}}\times \color{red}{h}\\
\frac{64}{3}&=&\frac{1}{3}\times \color{magenta}{\frac{1}{2}\times 4\sqrt{2}\times 6\sqrt{2}}\times \color{red}{h}\\
64&=&24\,\color{red}{h}\\
\color{red}{h}&=&\underline{\underline{ \frac{8}{3} }}(\mathrm{cm})
\end{eqnarray}\)
転がしても元の体積は変わらない、というのがポイントです。
(2)
正方形が２つあります。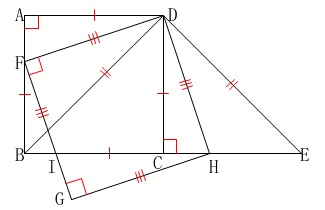
簡単にですが条件を書き込むと図のようになります。
\(\,\mathrm{△DBE}\,\)だけでなく、
\(\,\mathrm{△ABD\,,\,△CBD\,,\,△CED}\,\)も直角二等辺三角形です。
ア
\(\,\mathrm{△DFB}\,\)と\(\,\mathrm{△DHE}\,\)が合同であることの証明です。
四角形\(\,\mathrm{DFGH}\,\)が正方形だから
\(\hspace{10pt}\mathrm{DF=DH} ･･･②\)
がいえるので直角三角形の合同条件から
\(\hspace{10pt}\mathrm{△DAF}\,\)≡\(\,\mathrm{△DCH}\,\)
このことが問題に書いてあるので証明は簡単ですが、
長さの等しいこと
\(\hspace{10pt}\mathrm{FB=HE}\)
ではなく、間の角が等しい方向で証明が進んでいえるので
\(\hspace{10pt}\mathrm{∠FDB=∠HDE} ･･･③\)
①②③から
「\(\underline{ ２組の辺とその間の角 }\)がそれぞれ等しい。」
という合同条件になるので３辺がそれぞれ等しいという合同条件は選択できません。
自分で証明するときはどちらでも良いですけど、
流れにのって証明すれば良いので問題の方が進みやすいでしょう。
イ
長さが与えられて\(\,\mathrm{△FBI}\,\)の面積を求めます。
アで見たように、
\(\,\mathrm{△DAF}\,\)≡\(\,\mathrm{△DCH}\,\)
なので
\(\hspace{10pt}\mathrm{AF=CH}=2\)
また
\(\hspace{10pt}\mathrm{FB}=\mathrm{AB-AF}=3\)
詳しく説明すると長くなるので省略しますが
\(\hspace{10pt}\mathrm{△DAF}\,\)∽\(\,\mathrm{△FBI}\,\)
※
角度に注目するとすぐに分かります。
このとき相似比は\(\,5:3\,\)なので、
\(\hspace{10pt}\displaystyle \mathrm{△DAF}=\frac{1}{2}\times 5\times 2=5\)
であることから
\(\begin{eqnarray}
\mathrm{△DAF:△FBI}&=&5^2:3^2\\
5:\mathrm{△FBI}&=&25:9\\
\mathrm{△FBI}&=&\underline{\underline{ \frac{9}{5} }}\,(\mathrm{cm^2})
\end{eqnarray}\)
相似な図形の面積比は、
相似比の２乗になることは忘れないようにしましょう。
第４問
\(\large{\color{black}{\fbox{4}}}\)
関数です。
条件は
\(\hspace{10pt}y=ax^2 (\,a\,＞\,0\,) ･･･①\)
点\(\,\mathrm{A}\,\)の\(\,x\,\)座標は\(\,2\,\)、
\(\,\mathrm{B}\,\)は\(\,x\,\)軸上の点で\(\,x\,\)座標は\(\,\mathrm{A}\,\)と同じ。
点\(\,\mathrm{B}\,\)の\(\,x\,\)座標も\(\,2\,\)です。
これは全体に通じる条件なので忘れないようにしましょう。
※
長さの単位は\(\,\mathrm{cm}\,\)ですが省略しています。
(1)
比例定数が決まっている場合と、
比例定数が決まっていない問題です。
問題の条件では決まっていない方が通常なので後で間違えないようにしたいところですが、
ここでは比例定数を求める形の問題になっているので余り気にしなくて良いですね。
ア
比例定数が決まっている問題です。
\(\hspace{10pt}\displaystyle y=\frac{1}{2}\,x^2\)
点\(\,\mathrm{A}\,\)の\(\,x\,\)座標は\(\,\color{red}{2}\,\)なので\(\,y\,\)座標は
\(\begin{eqnarray}
y&=&\frac{1}{2}\times \,(\,\color{red}{2}\,)^2\\
&=&\underline{ 2 }
\end{eqnarray}\)
イ
比例定数を求める問題です。
\(\,\mathrm{A\,,\,B}\,\)の距離は\(\,x\,\)座標が同じなので\(\,y\,\)座標の差が距離になります。
点\(\,\mathrm{A}\,\)の座標は\(\,a\,\)用いて表すと
\(\hspace{10pt}(\,2\,,\,\color{red}{4a}\,)\)
なので\(\,\mathrm{B}\,\)の\(\,y\,\)座標が\(\,\color{blue}{0}\,\)であることから
\(\begin{eqnarray}
\color{red}{4a}-\color{blue}{0}&=&6\\
a&=&\underline{\underline{ \frac{3}{2} }}
\end{eqnarray}\)
比例\(\,y=ax\,\)だけでなく\(\,y=ax^2\,\)でも\(\,a\,\)は比例定数ですよ。
(2)
条件に図形と点が加わります。
正方形\(\,\mathrm{ABCD}\,\)
点\(\,\mathrm{E}\,\)は\(\,①\,\)上の点で\(\,x\,\)座標は\(\,-1\,\)
他の条件は全体で同じです。
ア
直線\(\,\mathrm{BD}\,\)は正方形\(\,\mathrm{ABCD}\,\)の対角線になっています。
正方形の対角線は\(\,45°\,\)を作ることと\(\,\mathrm{BC}\,\)が\(\,x\,\)軸と重なっていることから、
傾きは\(\,1\,\)になるので
\(\hspace{10pt}y=x+b\)
点\(\,\mathrm{B}\,\)は\(\,(\,2\,,\,0\,)\,\)だから、
\(\begin{eqnarray}
0&=&2+b\\
b&=&-2
\end{eqnarray}\)
\(\hspace{10pt}\underline{ y=x-2 }\)
\(\,y\,\)切片を求めて１次関数の形で答えにしていますが、
両切片を求めてから
\(\hspace{10pt}x-y=2\)
でもいいと思います。
イ
\(\,\mathrm{△BDE}\,\)の面積が\(\,80\,\)となるときの\(\,①\,\)の比例定数を求めます。
座標がないと考えにくいので\(\,a\,\)を使って座標を書き出します。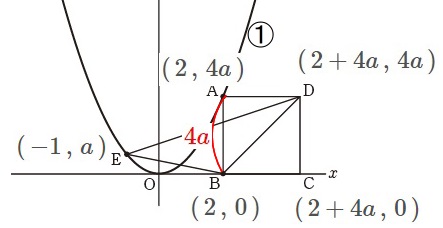
正方形\(\,\mathrm{ABCD}\,\)の\(\,1\,\)辺が\(\,\color{red}{4a}\,\)なので座標はそれぞれ
\(\hspace{4pt}\mathrm{B}\,(\,2\,,\,0\,)\,\)
\(\hspace{4pt}\mathrm{A}\,(\,2\,,\,4a\,)\,\)
\(\hspace{4pt}\mathrm{C}\,(\,2+4a\,,\,0\,)\,\)
\(\hspace{4pt}\mathrm{D}\,(\,2+4a\,,\,4a\,)\,\)
\(\hspace{4pt}\mathrm{E}\,(\,-1\,,\,a\,)\,\)
となります。
(2)イ図形的に計算する方法
ここからは簡単で長方形から三角形を引けば面積は表せます。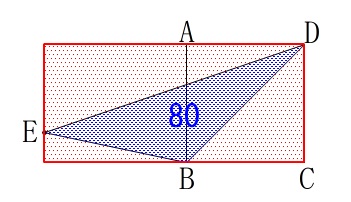
長方形の面積から３つの三角形の面積を引きますが、
長さは\(\,a\,\)を使った文字式になるので長さを書き込んで行きます。
長方形の横の長さは\(\,\mathrm{E}\,\)と\(\,\mathrm{D}\,\)の\(\,x\,\)座標の差から
\(\hspace{10pt}2+4a-(-1)=\,\color{red}{4a+3}\)
縦の長さは\(\,\mathrm{A}\,\)と\(\,\mathrm{B}\,\)の\(\,y\,\)座標の差から
\(\hspace{10pt}4a-0\,=\,\color{blue}{4a}\)
また座標からそれぞれの辺の長さは図のようになります。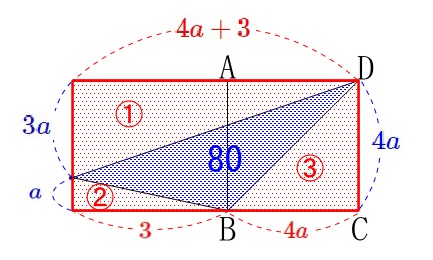
これから計算すると、
長方形の面積が
\(\hspace{10pt}(4a+3)\times 4a=16a^2+12a\)
３つの直角三角形の面積が
\(\hspace{10pt}\displaystyle \color{red}{①}=\frac{1}{2}\times (4a+3)\times (3a)\)
\(\hspace{10pt}\displaystyle \color{red}{②}=\frac{1}{2}\times 3\times a\)
\(\hspace{10pt}\displaystyle \color{red}{③}=\frac{1}{2}\times 4a\times 4a\)
なので
\(\begin{eqnarray}
(16a^2+12a)-(①+②+③)&=&80\\
16a^2+12a-(14a^2+6a)&=&80\\
2a^2+6a&=&80\\
a^2+3a-40&=&0\\
(a+8)(a-5)&=&0\\
a&=&-8\,,\,5
\end{eqnarray}\)
条件から\(\,a＞0\,\)なので
\(\hspace{10pt}a=\underline{ 5 }\)
ただ、会員のみんなには\(\,\mathrm{B}\,\)を原点に移してから計算して欲しいです。
というか『超え太郎』に取り組んできた会員は平行移動してから計算していると思います。
（平行移動していると信じたい？）
「公式を使って」ということではなく、
公式を使うためにどういう手順で説明していたかカードで順になっていたはずだから。
全体を\(\,x\,\)軸方向に\(\,-2\,\)だけ平行移動します。
点\(\,\mathrm{B}\,\)は原点に移動するので
\(\hspace{4pt}\mathrm{B’}\,(\,0\,,\,0\,)\,\)
他の点の移動もすませると
\(\hspace{4pt}\mathrm{A’}\,(\,0\,,\,4a\,)\,\)
\(\hspace{4pt}\mathrm{C’}\,(\,4a\,,\,0\,)\,\)
\(\hspace{4pt}\mathrm{D’}\,(\,4a\,,\,4a\,)\,\)
\(\hspace{4pt}\mathrm{E’}\,(\,-3\,,\,a\,)\,\)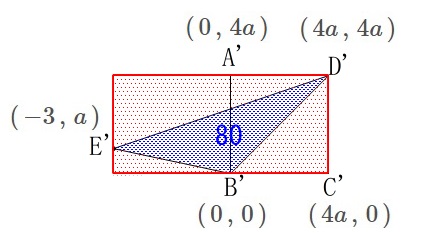
こう見ると先ほど面積計算で使った長さは分かり易いでしょう。
もちろん、平行移動が先に浮かんだ会員は
\(\hspace{4pt}\mathrm{B’}\,(\,0\,,\,0\,)\,\)
\(\hspace{4pt}\mathrm{D’}\,(\,4a\,,\,4a\,)\,\)
\(\hspace{4pt}\mathrm{E’}\,(\,-3\,,\,a\,)\,\)
だけから
\(\begin{eqnarray}
\left|\frac{4a\times a-4a\times (-3)}{2}\right|&=&80\\
|4a^2+12a|&=&160\\
|a^2+3a|&=&40\\
a^2+3a-40&=&0
\end{eqnarray}\)
としているでしょう。
※
絶対値に関しては\(\,a\,\)が正だから外しやすい。
使って良いので使い倒して下さい。
(2)イ普通に誘導に乗って等積移動する方法
ところで、この問題を普通にアの誘導から考えれば、
点\(\,\mathrm{E}\,\)を通り傾きが\(\,1\,\)の直線を利用して等積移動するでしょう。
点\(\,\mathrm{E}\,(\,-1\,,\,a\,)\,\)を通り傾きが\(\,1\,\)の直線は
\(\hspace{10pt}y=x+1+a\)
この直線上で\(\,x=2\,\)のときの座標は
\(\hspace{10pt}\color{red}{(\,2\,,\,3+a\,)}\)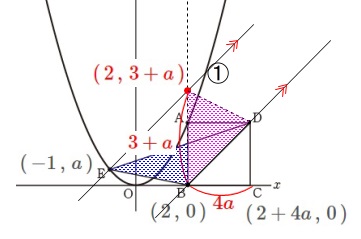
このことから
\(\,\mathrm{△BED}\,\)の面積が\(\,80\,\)になるのは
底辺を\(\,y\,\)軸に平行な線分\(\,3+a\,\)、
高さを\(\,x\,\)座標の差\(\,4a\,\)と見て
\(\begin{eqnarray}
\frac{1}{2}\times (3+a)\times 4a&=&80\\
4a^2+12a&=&160\\
a^2+3a-40&=&0\\
(a+8)(a-5)&=&0\\
a&=&-8\,,\,5
\end{eqnarray}\)
条件から\(\,a\,＞\,0\,\)なので
\(\hspace{10pt}a=\underline{ 5 }\)
直線の切片が利用できるわけではないですが、
底辺を\(\,\mathrm{BD}\,\)と見て等積移動させるのがポイントです。
（問題の求めているのはこちらかな？）
いずれにしても\(\,\mathrm{B}\,\)の\(\,x\,\)座標は大活躍ですね。
第５問
\(\large{\color{black}{\fbox{5}}}\)
連立方程式と整数の文章問題です。
関数にも見えますが個数の問題なので整数ですよ。
日本語が多く\(\color{black}{\fbox{2}}\)同様に穴埋めがあります。
順に埋めていけばそれ程ややこしい問題でもないでしょう。
【問題】と〔条件〕があり、(1)と(2)で条件は変わりますが【問題】は同じです。
【問題】の要点をまとめると、
・りんご１個の値段は１２０円
・なし１個の値段は１５０円
・４０円の箱に詰めて合計で６７００円にする。
(1)
〔条件〕は「りんごとなし合わせて５０個」です。
ここは文字１つで済ますか文字２つ使って連立方程式にするかなので簡単にすませます。
〔マユさん〕
りんごを\(\,a\,\)個とすると合わせて５０個なので、
なしは\(\,\underline{ 50-a }\,\)個と表すことができます。
りんご分の金額は\(\,\color{red}{120\times a}\,\)円、
なしの分の金額は\(\,\color{blue}{150\times (50-a)}\,\)円なので、
箱代と合わせて方程式を立てて解くと
\(\begin{eqnarray}
\color{red}{120a}+\color{blue}{150(50-a)}+40&=&6700\\
a&=&28
\end{eqnarray}\)
〔リクさん〕
りんごを\(\,a\,\)個、なしを\(\,b\,\)個とすると、
合わせて５０個なので
\(\hspace{10pt}\underline{ a+b=20 }\)
合計金額から方程式を立てると
\(\hspace{10pt}\underline{ 120a+150b+40=6700 }\)
これらを連立したものが答えです。
\( \begin{cases}
\hspace{4pt} a+b=50\\
\hspace{4pt} 120a+150b+40=6700
\end{cases}\)
当然ですが解となる個数は同じです。
(2)
〔条件〕が変わります。
〔条件\(\,\mathrm{A}\,\)〕りんごとなしはどちらも\(\,18\,\)個以上。
〔条件\(\,\mathrm{B}\,\)〕りんごとなしは合計\(\,50\,\)個より多く。
文字式で表しておきたいところですが、
〔解答〕の中で\(\,x\,,\,yを\,\)使って表されているので従います。
〔解答〕
りんごの個数を\(\,x+18\,\)、なしの個数を\(\,y+18\,\)とする。
ア 箱代や合計金額は変わらないので
\(\hspace{4pt}\underline{ 120(x+18)+150(y+18)+40 }=6700\)
イ
この方程式の係数を見やすくすると
\(\hspace{10pt}4a+5y=60\)
これは直線を表す式で条件を満たす整数\(\,x\,,\,y\,\)は\(\,4\,\)組あります。
直感的に求めるならグラフから格子点となる点を見つけます。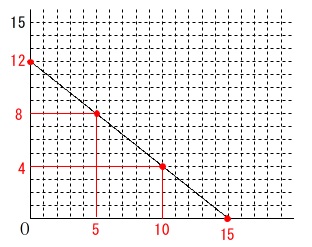
整数なので\(\,x\,\)が\(\,0\,\)のとき、\(\,y\,\)が\(\,0\,\)のとき、
条件を満たすので直線の切片からもグラフはかけます。
もちろん式を変形して、
\(\hspace{10pt}\displaystyle y=-\frac{4}{5}\,x+12\)
からでも同じです。
このグラフと\(\,x\,,\,y\,\)が両方整数となる点（格子点）を探すだけです。
\(\hspace{4pt}(\,x\,,\,y\,)=\underline{ (0\,,\,12),(5\,,\,8),(10\,,\,4),(15\,,\,0) }\)
整理された直線の式は
\(\hspace{10pt}\displaystyle y=-\frac{4}{5}\,x+12\)
なので\(\,x\,,\,y\,\)は個数なのでともに整数だから
\(\hspace{4pt}\,\color{red}{x\,は\,5\,の倍数}\)
でなければ\(\,y\,\)が整数にならないので順に探していっても良いです。
ここで出てきた\(\,x\,,\,y\,\)をりんごとなしの個数に変えると、
（両方に\(\,18\,\)ずつ足します。）
\(\begin{eqnarray}
(\,x\,,\,y\,) &\rightarrow &(\,りんご\,,\,なし\,)\\
(\,0\,,\,12\,) &\rightarrow &(\,18\,,\,30\,)\\
(\,5\,,\,8\,) &\rightarrow &(\,23\,,\,26\,)\\
(\,10\,,\,4\,) &\rightarrow &(\,28\,,\,22\,)\\
(\,15\,,\,0\,) &\rightarrow &(\,33\,,\,18\,)\end{eqnarray}\)
この中で〔条件\(\,\mathrm{B}\,\)〕を満たすのは
\(\hspace{10pt}(\,x\,,\,y\,)=(\,15\,,\,0\,)\)
だけなので、
りんご \(\,\underline{ 33 }\,\)個 なし\(\,\underline{ 18 }\,\)個
\(\,(\,x\,,\,y\,)=(\,10\,,\,4\,)\)のときは合計\(\,50\,\)個です。
〔条件\(\,\mathrm{B}\,\)〕は「５０個より多く」なので満たしていません。
この問題のポイントは問題の流れを利用するということと、
地道にコツコツ調べることも数学、
だということです。
〔解答〕の手順ではなく、
りんごとなしをそれぞれ\(\,a\,,\,b\,\)個としても、
（整数の組は出しにくいですが、）
最後の答えは同じになることを確認しても良いですね。
以上です。
青森県の過去問を数年分見ればわかると思いますが、
過度な難問はなく、偏りのある出題でもありません。
ただ、高得点を目標にするならどのくらいの作業が必要かは知っておくと良いです。
当然ですが偏りのない基礎をしっかり固めることが一番の対策になりますね。
クラブ活動で忙しい！
塾に通っているのに数学が苦手！
数学の勉強時間を減らしたい！
数学の勉強方法が分からない！
その悩み、『覚え太郎』が解決します！！！
