2023年(令和5年)度三重県公立高校入試後期【数学】の問題と解説

2023年(令和5年)度三重県公立高校入試後期選抜【数学】の問題と解説です。
前期と比べると、と言うほどは変わりはなく基本中心の問題構成ですが、
多少計算ミスを誘う問題が並ぶので暗算しすぎないようにすれば高得点は狙えるでしょう。
三重県は毎年偏った問題にはならないことを再認識してください。

2023年(令和5年)度三重県公立高校入試後期選抜【数学】の問題

令和５年度の後期選抜試験の数学問題です。

⇒　2023年(令和5年)度三重県公立高校入試後期選抜【数学】の問題PDF

偏りの無い問題構成は毎年変わりありません。

2023年(令和5年)度三重県公立高校入試後期選抜【数学】の解説

大問７つは前期も同じですが、
前期より若干計算ミスを起こしやすい問題なので、
気をつけないと大きな差になりますよ。
（対策ページではないのでクドくはいいません。）

前期の問題を解説しているときに「後期で詳しく解説する」と書いたのですが、
問題を解いてみて気が変わりました。
しつこい解説はやめておきます。
※
三重県の問題はクセが少なく基本中心、偏りの無い問題構成です。
令和５年度の問題も会員には何度も解説してきたことなので、
復習をしっかりすれば問題ありません。

第１問小問集合

\(\large{\color{black}{\fbox{1}}}\)
早速見ていきます。
(1)
　\(\hspace{10pt}4-(-3)\\
=4+3\\
=\underline{　7　}\)

時間のことを考えると暗算したくなりますが、
問題にスペースくれているので確実に。
(2)
　\(\hspace{10pt}6(2x-5y)\\
=\underline{　12x-30y　}\)

これは暗算も何も展開するだけです。
(3)
　\(\hspace{10pt}\displaystyle \color{red}{\frac{5}{\sqrt{5}}}+\color{blue}{\sqrt{20}}\\
\displaystyle =\color{red}{\frac{5\sqrt{5}}{5}}+\color{blue}{2\sqrt{5}}\\
=\sqrt{5}+2\sqrt{5}\\
=\underline{　3\sqrt{5}　}\)

練習量にもよるのですが３行目はなくても、
分母の有理化と素因数分解はやった方が良いです。
(4)
　\(\hspace{10pt}x^2-5x+4\\
=\underline{　(x-4)(x-1)　}\)

「因数分解しなさい。」というのだから因数分解できるんです。
定数項に着目ですね。
(5)
２次方程式を解きます。
　\(\hspace{10pt}3x^2-7x+1=0\)
因数分解できないので解の公式です。
　\(\begin{eqnarray}
x&=&\frac{-(-7)\pm \sqrt{(-7)^2-4\cdot 3\cdot (1)}}{2\times 3}\\
&=&\frac{7\pm \sqrt{49-12}}{6}\\
&=&\underline{\underline{　\frac{7\pm \sqrt{37}}{6}　}}
\end{eqnarray}\)
※
ルートの中の「\(\,\cdot\,\)」は掛け算の意味です。
(6)
分母が３の分数が整数になるということは分子が３の倍数です。
かつ、ルートの中が平方数になれば整数になるので、
　\(\hspace{10pt}40\,n=2^3\times 5\times n=2^2\times \color{red}{2\times 5}\times n\)
と素因数分解すると平方数になっていない部分と、
分子が\(\,\color{blue}{３の倍数になる}\,\)ことを考えて
　\(\hspace{10pt}n=\color{red}{2\times 5\times k^2}\times \color{blue}{3^2}\)
となっていれば
　\(\hspace{10pt}\displaystyle \frac{\sqrt{40\,n}}{3}\\
\displaystyle =\frac{\sqrt{2^2\times 2^2\times 5^2\times 3^2\times k^2}}{3}\\
\displaystyle =\frac{2\times 2\times 5\times 3\times k}{3}\\
=20\,k\)
となり\(\,k\,\)が整数であれば全体が整数になります。
最小の自然数\(\,n\,\)は\(\,k=1\,\)のときで
　\(\hspace{10pt}n=\underline{　90　}\)
※
\(\,k\,\)は整数ですが\(\,k=0\,\)では\(\,n\,\)が自然数になりません。

先ずはルートを外すことを考えると、
　\(\hspace{10pt}40=2^2\times \color{red}{2\times 5}\times n\)
\(\,n\,\)は\(\,\color{red}{2\times 5}\,\)を因数に持って、
さらに\(\,3\,\)の倍数にならなければいけないので\(\,9\,\)も因数に持つ。
だから\(\,n=2\times 5\times 9=90\,\)でも最小の自然数が求まります。
(7)
「比例」なので\(\hspace{4pt}y=a\,x\)とおく。
\(\,x=10\,\)のとき\(\,y=-2\,\)なので
　\(\begin{eqnarray}
-2&=&a\times (10)\\
a&=&-\frac{1}{5}　(比例定数)
\end{eqnarray}\)
関数は\(\displaystyle \,y=-\frac{1}{5}\,x\,\)と決まります。
\(\displaystyle \,y=\frac{2}{3}\,\)となるのは
　\(\begin{eqnarray}
\frac{2}{3}&=&-\frac{1}{5}\,x\\
x&=&\underline{\underline{　-\frac{10}{3}　}}
\end{eqnarray}\)

関数の決定が先です。（１行目に注目。）
(8)
角度を求めます。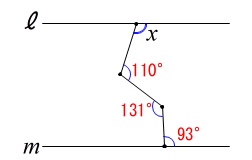平行線の同位角、錯角が等しくなる事を利用したいので、
平行線を引きまくれば良いです。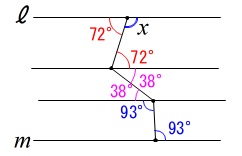下から順に角度を書き込んで行けば出ます。
　\(\begin{eqnarray}
∠x&=&180°-72°\\
&=&\underline{　108°　}
\end{eqnarray}\)

二桁の引き算があります。
暗算してミスするのはもったいないですよ。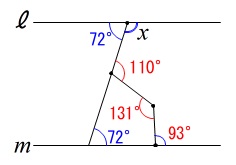四角形の内角の和からでも良いです。
他の延長線引いて求める方法をもありますが、
平行線を引いて錯角利用だけで十分でしょう。
(9)
ねじれの位置についてです。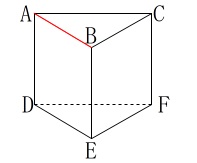直線\(\,\mathrm{AB}\,\)と交わりもなく、平行でもない直線を見つけますが、
逆に交わりを持つ直線や平行な直線を消せば分かり易いです。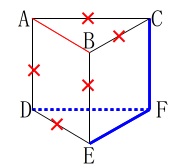問題では消せないので\(\,\color{red}{×}\,\)で示しました。
\(\,直線\mathrm{CF}\,,\,\mathrm{EF}\,,\,\mathrm{FD}\,\)がねじれの位置にあります。
答え\(\hspace{10pt}\underline{　オ　キ　ク　}\)

⇒　空間図形の位置関係問題(平行,ねじれの位置,垂直な面,平行な面)

立体の線や面の位置関係は計算では出せません。
(10)
ヒストグラムにおける最頻値です。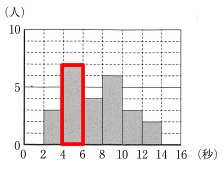階級はすぐに分かります。
ヒストグラムや度数分布表における最頻値はその階級の中央値です。
　\(\hspace{10pt}\underline{　5　}(秒)\)

⇒　代表値とは？度数分布表の平均値,中央値の求め方と最頻値の答え方

小学校の内容になりますが「代表値」はいらなくなるわけではありません。
(10)
円の作図です。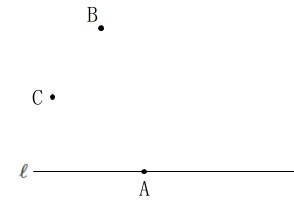条件は２つあります。
「直線\(\,\ell\,\)と点\(\,\mathrm{A}\,\)で接する。」
「中心が２点\(\,\mathrm{B\,,\,C}\,\)から等しい距離にある。」

円は中心と半径が必要です。
作図の手順は条件の順で良いです。
中心は点\(\,\mathrm{A}\,\)を通り\(\,\ell\,\)に垂直な直線上にあります。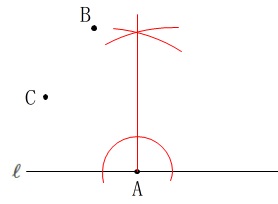２点から等しい距離にあるのは垂直二等分線です。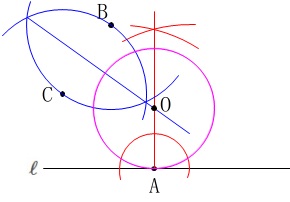交点\(\,\mathrm{O}\,\)が中心で、
線分\(\,\mathrm{OA}\,\)が半径の円を書けば終わりです。
（点\(\,\mathrm{O}\,\)を書く必要はありません。）

第２問箱ひげ図

\(\large{\color{black}{\fbox{2}}}\)
箱ひげ図の読み取りです。
問題の図１図２は自分で見てもらうとして問題に合わせて進めます。
(1)
四分位数です。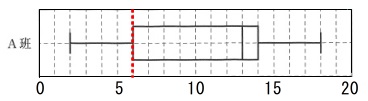第１四分位数は箱の左端になります。
答え\(\hspace{10pt}\underline{　6　}点\)
(2)
箱ひげ図とデータの照らしあわせです。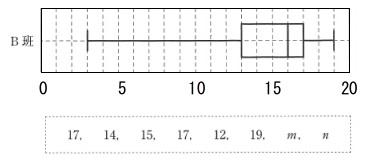条件は\(\,m\,＜\,n\,\)です。
箱ひげ図の最小値から\(\,m\,\)が最小値となります。
\(\hspace{10pt}m=\underline{　3　}\)

\(\,n\,\)はすぐに求まらないので、
\(\,n\,\)を除いた７人のデータを小さい順に並べて箱ひげ図を書きに行きます。
\(\hspace{10pt}3\,,\,12\,,\,14\,,\,\color{red}{15}\,,\,\color{red}{17}\,,\,17\,,\,19\)
\(\,\mathrm{B}\,\)班\(\,8\,\)人の中央値が\(\,16\,\)なので\(\,\color{red}{4}\,\)人目と\(\,\color{red}{5}\,\)人目は決まり。
\(\,n\,\)は中央値より大きい方に並ぶはず。
（\(\,\color{red}{15}\,\)以下だと中央値が箱ひげ図と合わせない。）
第３四分位数が\(\,\color{blue}{17}\,\)なので\(\,n\,\)は\(\,17\,\)となれば一致します。
\(\hspace{10pt}3\,,\,12\,,\,14\,,\,15\,,\,17\,,\,\color{blue}{17}\,,\,\color{blue}{17}\,,\,19\)
\(\hspace{10pt}n=\underline{　17　}\)

すぐに分かるわけではないので、
データを与えて四分位数を比べていくと良いです。
（８つのデータの四分位数はメンドウだけど。）
\(\hspace{10pt}○\,\color{magenta}{●}\,\color{magenta}{●}\,\color{red}{●}\,\color{red}{●}\,\color{blue}{●}\,\color{blue}{●}\,○\)
四分位数はそれぞれの色分けしたデータの平均値ですよ。
(3)
\(\,\mathrm{C}\,\)班は\(\,\mathrm{10}\,\)人です。
１０人のデータを小さい方から並べて、
第１四分位数は\(\,\color{magenta}{3}\,\)番目、
第２四分位数（中央値）は小さい方から\(\,\color{red}{5}\,\)番目と\(\,\color{red}{6}\,\)番目の値の平均値、
第３四分位数は\(\,\color{blue}{8}\,\)番目の値になります。
\(\hspace{10pt}○\,○\,\color{magenta}{●}\,○\,\color{red}{●}\,\color{red}{●}\,○\,\color{blue}{●}\,○\,○\)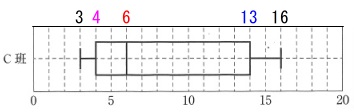最小値と最大値は分かっていますが他はわからないので、
四分位数を一致させるように\(\,\color{red}{5}\,\)番目と\(\,\color{red}{6}\,\)番目のデータを探します。
（第１四分位数は\(\,\color{magenta}{4}\,\)、中央値は\(\,\color{red}{6}\,\)、第３四分位数は\(\,\color{blue}{13}\,\)）
\(\hspace{10pt}3\,○\,\color{magenta}{4}\,○\,\color{red}{●}\,\color{red}{●}\,○\,\color{blue}{13}\,○\,16\)

第２四分位数（中央値）が\(\,\color{red}{6}\,\)なので、
\(\,5\,\)番目と\(\,6\,\)番目の平均が\(\,\color{red}{6}\,\)にならなければダメです。
つまり、２つの数の和が１２。

６番目が第３四分位数\(\,\color{blue}{13}\,\)以下と見て、
\(\,5\,\)番目と\(\,6\,\)番目の組は
（第１四分位数\(\,4\,\)以上になることを考えて）
\(\hspace{10pt}(\,6\,,\,6\,)\,(\,5\,,\,7\,)\,(\,4\,,\,8\,)\)
の３組しかありません。
答え\(\hspace{10pt}\underline{　6\,,\,7\,,\,8　}\)

第１四分位数\(\,\color{magenta}{4}\,\)以上、第３四分位数\(\,\color{blue}{13}\,\)以下で、
和が\(\,12\,\)なのでかなり絞ることができます。
（全て書き出してもそれ程多くない。）
(4)
箱ひげ図では読み取れないことがあります。
それがよく問題にされますね。
①
\(\,\mathrm{A}\,\)班と\(\,\mathrm{B}\,\)班の「範囲」は同じか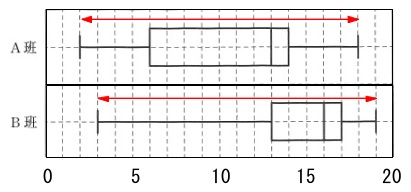？同じです。
答え\(\underline{　ア　}\)

「範囲」は最大値と最小値の差です。
②
全ての班に\(\,14\,\)点の人はいるか？

図\(\,2\,\)から\(\,\mathrm{B}\,\)班にはいますね。
しかし、(3)を見なおしてみてください。\(\hspace{10pt}3\,○\,\color{magenta}{4}\,○\,\color{red}{●}\,\color{red}{●}\,○\,\color{blue}{13}\,○\,16\)

\(\,\mathrm{C}\,\)班は\(\,14\,\)点の人はいなくても同じ箱ひげ図になります。
（例えば、\(\hspace{4pt}3\,○\,\color{magenta}{4}\,○\,\color{red}{●}\,\color{red}{●}\,○\,\color{blue}{13}\,13\,16\)）
ただし、\(\,14\,\)点の人がいても同じ箱ひげ図になるのでいないとも言えない。
（例えば、\(\hspace{4pt}3\,○\,\color{magenta}{4}\,○\,\color{red}{●}\,\color{red}{●}\,○\,\color{blue}{13}\,14\,16\)）
\(\,\mathrm{A}\,\)班についても同じです。（調べて見てください。）
答え\(\underline{　ウ　}\)
※
\(\,\mathrm{A}\,\)班の例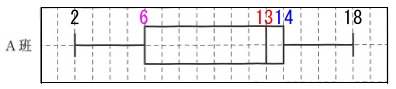\(\hspace{10pt}2\hspace{4pt}\color{magenta}{6}\hspace{4pt}\color{magenta}{6}\hspace{4pt}\color{red}{13}\hspace{4pt}\color{red}{13}\hspace{4pt}\color{blue}{13}\hspace{4pt}\color{blue}{15}\hspace{4pt}18\)
と
\(\hspace{10pt}2\hspace{4pt}\color{magenta}{6}\hspace{4pt}\color{magenta}{6}\hspace{4pt}\color{red}{13}\hspace{4pt}\color{red}{13}\hspace{4pt}\color{blue}{14}\hspace{4pt}\color{blue}{14}\hspace{4pt}18\)
同じ箱ひげ図になりませんか？

第３問連立方程式

\(\large{\color{black}{\fbox{3}}}\)
連立方程式の基本問題です。
(1)
「小学生と中学生合わせて\(\,120\,\)人」
　\(\color{black}{\fbox{ \(x\,+\,y\) }}\)\(\,=120\,\)
「小学生の\(\,35\,\)％と中学生の\(\,20\,\)％合わせて\(\,30\,\)人」
　\(\color{black}{\fbox{\(\displaystyle 　\frac{35}{100}\,x\,+\frac{20}{100}\,y　\)}}\)\(\,=30\,\)
または
　\(\color{black}{\fbox{ 　\(\displaystyle0.35\,x+0.20\,y\)　}}\)\(\,=30\,\)
（どちらでも良いですが％は\(\,100\,\)基準の方が楽です。）
(2)
(1)で立てた連立方程式を解くだけです。
　\(\hspace{10pt}x=40\,,\,y=80\)
答え\(\hspace{10pt}小学生\underline{　40　}人、中学生\underline{　80　}人\)

⇒　小数や分数が係数にある連立方程式をはやく解く解き方のコツ

今さらとは思いますが復習しておきましょう。

第４問確率

\(\large{\color{black}{\fbox{4}}}\)
確率です。
それぞれが持っているカード枚数は問題で確認しておいてください。
のぞみさんが袋に入れる枚数は決まっています。
(1)
けいたさんがグー\(\,1\,\)枚、チョキ\(\,2\,\)枚、パー\(\,1\,\)枚の場合。
複数枚あるカードを区別して樹形図でも良いですが、
ここでは表で見ておきます。（けいたさんが赤字）
　\(\begin{array}{|c|c|c|c|c|} \hline
& \color{red}{G} & \color{red}{C} & \color{red}{C} & \color{red}{P} \\ \hline
G & & & & ○ \\ \hline
G & & & & ○ \\ \hline
C & ○ & & & \\ \hline
P & & ○ & ○ & \\ \hline
\end{array}\)
けいたさんが勝つ確率は
\(\hspace{10pt}\displaystyle \underline{　\frac{5}{16}　}\)
(2)
けいたさんの枚数が変わります。（のぞみさんは変わりません。）
グー\(\,1\,\)枚、チョキ\(\,3\,\)枚、パー\(\,a\,\)枚。
これはパーの枚数を増やしていくと見えてくるのでは？
ということで\(\,a=1\,\)から見ていきます。
（\(\,○\,\)はけいたさんの勝ち、\(\,×\,\)はのぞみさんの勝ち）
\((\,\mathrm{ⅰ}\,)\,a=1\)
　\(\begin{array}{|c|c|c|c|c|c|} \hline
& \color{red}{G} & \color{red}{C} & \color{red}{C} & \color{red}{C} & \color{red}{P} \\ \hline
G & & × & × & × & ○ \\ \hline
G & & × & × & × & ○ \\ \hline
C & ○ & & & & × \\ \hline
P & × & ○ & ○ & ○ & \\ \hline
\end{array}\)
空白は「あいこ」です。
けいたさんの勝つ確率は\(\displaystyle \,\frac{6}{20}\)
のぞみさんの勝つ確率は\(\displaystyle \,\frac{8}{20}\)
あいこの確率は\(\displaystyle \,\frac{6}{20}\)
（分子合計が\(\,20\,\)になるか確認しています。）
\((\,\mathrm{ⅰ}\,)\,a=2\)
　\(\begin{array}{|c|c|c|c|c|c|c|} \hline
& \color{red}{G} & \color{red}{C} & \color{red}{C} & \color{red}{C} & \color{red}{P} & \color{red}{P}\\ \hline
G & & × & × & × & ○ & ○\\ \hline
G & & × & × & × & ○ & ○\\ \hline
C & ○ & & & & × & ×\\ \hline
P & × & ○ & ○ & ○ & & \\ \hline
\end{array}\)
けいたさんの勝つ確率は\(\displaystyle \,\frac{8}{24}\)
のぞみさんの勝つ確率は\(\displaystyle \,\frac{9}{24}\)
あいこの確率は\(\displaystyle \,\frac{7}{24}\)
（分子合計が\(\,24\,\)になるか確認しています。）
確率が近づいてきました。
\((\,\mathrm{ⅰ}\,)\,a=3\)
　\(\begin{array}{|c|c|c|c|c|c|c|} \hline
& \color{red}{G} & \color{red}{C} & \color{red}{C} & \color{red}{C} & \color{red}{P} & \color{red}{P} & \color{red}{P}\\ \hline
G & & × & × & × & ○ & ○ & ○\\ \hline
G & & × & × & × & ○ & ○ & ○ \\ \hline
C & ○ & & & & × & × & × \\ \hline
P & × & ○ & ○ & ○ & & & \\ \hline
\end{array}\)
けいたさんの勝つ確率は\(\displaystyle \,\frac{10}{28}\)
のぞみさんの勝つ確率は\(\displaystyle \,\frac{10}{28}\)
あいこの確率は\(\displaystyle \,\frac{8}{28}\)
（分子合計が\(\,28\,\)になるか確認しています。）
等しくなりました。
答え\(\hspace{10pt}\underline{　a=3　}\)

文字式使って計算で出そうと思えば出せるかもしれませんが、
場合を考える問題だと思います。
ちなみにパーだけが増えると問題を読み取ったとき、
　\(\begin{array}{|c|c|c|c|c|c|c} \hline
& \color{red}{G} & \color{red}{C} & \color{red}{C} & \color{red}{C} & \color{red}{P} & 　 & 　\\ \hline
G & & & & & & & \\ \hline
G & & & & & & & \\ \hline
C & & & & & & & \\ \hline
P & & & & & & & \\ \hline
\end{array}\)
のような表がかけるスペースが下に作ってあるのだと感じました。

大問１問確率にあててくる場合、
作業なくして答えは出ないと思って良いです。

第５問関数

\(\large{\color{black}{\fbox{5}}}\)
見た瞬間に分かるように関数です。
条件を一通り見ておきます。
\(\hspace{10pt}\displaystyle y=\frac{1}{4}\,x^2　･･･㋐\)
\(\hspace{10pt}\displaystyle y=a\,x+b　･･･㋑\)
交点\(\,\mathrm{A}\,\)の\(\,x\,\)座標は\(\,-6\,\)、\(\,\mathrm{B}\,\)の\(\,x\,\)座標は\(\,2\,\)。
点\(\,\mathrm{C}\,\)は\(\,㋐\,\)上の点で\(\,x\,\)座標が\(\,4\,\)。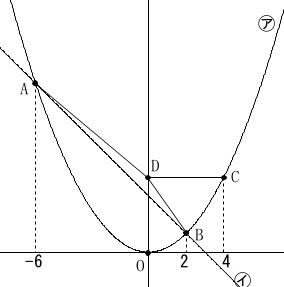一気に分かることが増えますが、
問に沿っていきます。
(1)
点\(\,\mathrm{B}\,\)は\(\,㋐\,\)上の点で\(\,x\,\)座標が\(\,2\,\)なので
　\(\begin{eqnarray}
y&=&\frac{1}{4}\times (2)^2\\
&=&1
\end{eqnarray}\)
\(\hspace{10pt}\mathrm{B}\,\underline{　(\,2\,,\,1\,)　}\)
(2)
直線\(\,㋑\,\)の傾きと\(\,y\,\)切片を求めます。
（直線㋑の式を求めなさい、ということです。）
\(\,㋐\,\)上の点\(\,\mathrm{A}\,\)の座標は\(\,x\,\)座標が\(\,-6\,\)と分かっているので
\(\hspace{10pt}\mathrm{A}\,(\,-6\,,\,9\,)\)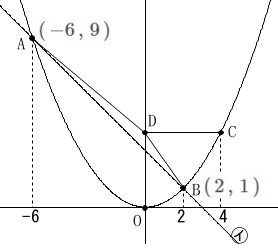２点\(\,\mathrm{A\,,\,B}\,\)を通る直線は
\(\hspace{10pt}y=-x+3\)
答え\(\hspace{4pt}\underline{　a=-1　}\,,\,\underline{　b=3　}\)

⇒　変化の割合とは？1次関数の求め方と直線の方程式との違い

直線は傾きから求めて行けば早いです。
(3)
\(\,\mathrm{△ABD}\,\)の面積です。
\(\hspace{10pt}\mathrm{C}\,(\,4\,,\,4\,)\)
\(\hspace{10pt}\mathrm{D}\,(\,0\,,\,4\,)\)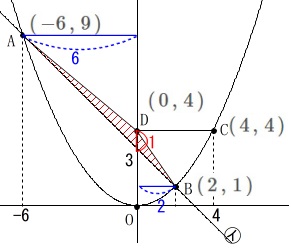底辺を点\(\,\mathrm{D}\,\)と\(\,㋑\,\)の\(\,y\,\)切片までの\(\,\color{red}{1}\,\)として、
（(2)で\(\,㋑\,\)は\(\,y=-x+3\,\)と分かっています。）
高さは２点\(\,\mathrm{A\,,\,B}\,\)の\(\,x\,\)座標の絶対値なので、
　\(\begin{eqnarray}
\mathrm{△ABD}&=&\frac{1}{2}\times \color{red}{1}\times (\,\color{blue}{6}+\color{blue}{2}\,)\\
&=&\underline{　4　}\,(\,\mathrm{cm^2}\,)
\end{eqnarray}\)
底辺が同じだから一度に計算していますが、
２つの三角形の面積を足しているのと同じです。

(4)
点\(\,\mathrm{E}\,\)は\(\,㋑\,\)上の点です。
条件は\(\,\mathrm{△CDE}\,\)が「\(\,\mathrm{ＣＤ=ＣＥ}\,\)」の二等辺三角形になること。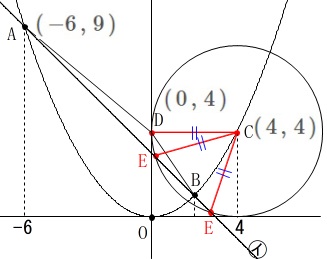図形的には点\(\,\mathrm{C}\,\)を中心として、
半径を\(\,\mathrm{DC}\,\)とする円と\(\,㋑\,\)との交点が点\(\,\mathrm{E}\,\)です。

ここでは三平方の定理を利用して機械的に処理します。
\(\,㋑\,\)上の点\(\,\mathrm{E}\,\)を\(\,(\,t\,,\,-t+3\,)\,\)と置いて、
点\(\,\mathrm{C}\,\)との距離\(\,\mathrm{CE}\,\)を\(\,\mathrm{DC=4}\,\)として方程式を立てます。
\(\hspace{10pt}\mathrm{C}\,(\,4\,,\,4\,)\)
\(\hspace{10pt}\mathrm{E}\,(\,t\,,\,-t+3\,)\)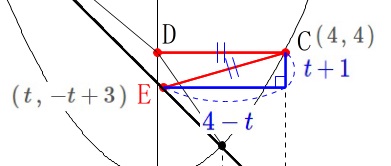２点\(\,\mathrm{C\,,\,E}\,\)の距離は直角三角形から
\(\begin{eqnarray}\displaystyle \mathrm{CE}&=&\sqrt{(4-t)^2+\{4-(-t+3)\}^2}\\
&=&\sqrt{(t-4)^2+(t+1)^2}\\
&=&\sqrt{t^2-8t+16+t^2+2t+1}\\
&=&\sqrt{2t^2-6t+17}
\end{eqnarray}\)
これが\(\,\mathrm{DC}\,\)と等しいことから両辺平方しても成り立つので
　\(\begin{eqnarray}
\mathrm{CE^2}&=&\mathrm{DC^2}\\
2t^2-6t+17&=&16\\
2t^2-6t+1&=&0\\
t&=&\frac{-(-6)\pm \sqrt{(6)^2-4\cdot 2\cdot 1}}{2\times 2}\\
&=&\frac{6\pm \sqrt{36-8}}{4}\\
&=&\frac{6\pm \sqrt{28}}{4}\\
&=&\frac{6\pm 2\sqrt{7}}{4}\\
&=&\underline{\underline{　\frac{3\pm \sqrt{7}}{2}　}}
\end{eqnarray}\)

点\(\,\mathrm{E}\,\)の\(\,x\,\)座標を求めるのでこれが答えです。
※
２次方程式は１次の係数が偶数なので
　\(\begin{eqnarray}
t&=&\frac{3\pm \sqrt{9-2}}{2}\\
&=&\frac{3\pm \sqrt{7}}{2}
\end{eqnarray}\)
知っているなら使って良いです。

⇒　２次方程式の解の公式二通りの求め方と便利な公式と文章題の解き方

解の公式は「覚えて使う」で良いですよ。

第６問平面図形

\(\large{\color{black}{\fbox{6}}}\)
平面図形で相似と線分の長さですが条件をしっかり読み取れば軽めです。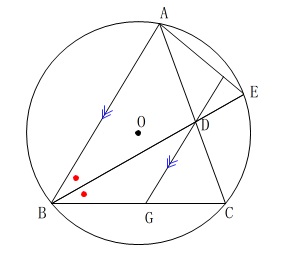(1)
先ずは相似の証明です。
\(\hspace{10pt}\mathrm{△ABD}\,\)∽\(\,\mathrm{△DAF}\,\)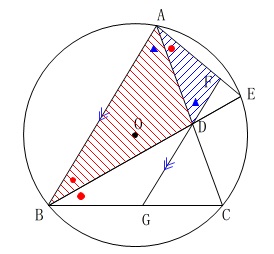円周角と平行線の錯角が等しくなる事から証明は終わりです。
線分\(\,\mathrm{BE}\,\)は\(\,\mathrm{∠ABC}\,\)の二等分線なので、
「仮定」として\(\,\mathrm{∠ABD=∠CBD}\,\)は言って良いです。

（証明）に必要な条件と流れ。
　\(\,\mathrm{△ABD}\,\)と\(\,\mathrm{△DAF}\,\)において
\(\hspace{10pt}\mathrm{\color{red}{∠ABD}=\color{blue}{∠CBD}}　(仮定)　･･･①\)
\(\hspace{10pt}\mathrm{\color{blue}{∠CBD}=\color{red}{∠DAF}}　(同一弧の円周角)　･･･②\)
\(\,①②\,\)から
\(\hspace{10pt}\mathrm{\color{red}{∠ABD}=\color{red}{∠DAF}}　･･･③\)
また
\(\hspace{10pt}\mathrm{∠BAD=∠ADF}　（平行線の錯角)･･･④\)
\(\,③④\,\)から相似条件は「２組の角がそれぞれ等しい。」です。

⇒　中学の図形証明問題(合同･相似)の解き方と証明の書き方ポイント

後は自分で書きやすいようにまとめれば良いです。

(2)
長さの条件が加わります。
\(\hspace{10pt}\mathrm{AD}=6\,,\,\mathrm{DF}=3\,,\,\mathrm{BC}=10\)※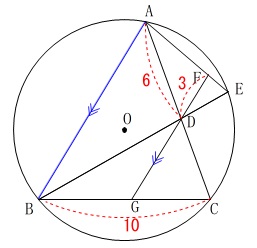
長さの単位は\(\,\mathrm{cm}\,\)です。
①
線分\(\,\mathrm{AB}\,\)の長さは(1)で証明した相似から求まります。
\(\hspace{10pt}\mathrm{△ABD}\,\)∽\(\,\mathrm{△DAF}\,\)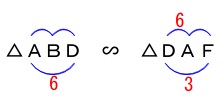　\(\begin{eqnarray}
\mathrm{AB:DA}&=&\mathrm{AD:DF}\\
\mathrm{AB}:6&=&6:3\\
\mathrm{AB}&=&\underline{　12　}\,(\,\mathrm{cm\,})
\end{eqnarray}\)
②
三重県では良く利用されていた気がします。

6-(2)②定理を利用した方法

内角の二等分線定理です。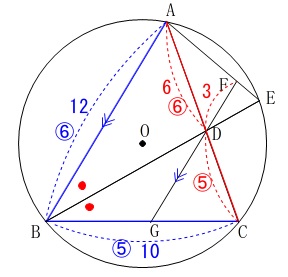\(\begin{eqnarray}
\mathrm{AB:BC}&=&\mathrm{AD:DC}\\
12:10&=&\color{red}{⑥}:\color{red}{⑤}
\end{eqnarray}\)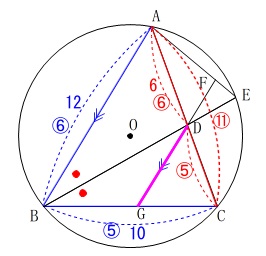\(\,\mathrm{△CDG}\,\)∽\(\,\mathrm{△CAB}\,\)なので、
　\(\begin{eqnarray}
\mathrm{DG}&=&\frac{\color{red}{5}}{\color{red}{6}+\color{red}{5}}\times \mathrm{\color{blue}{AB}}\\
&=&\frac{5}{11}\times \color{blue}{12}\\
&=&\underline{\underline{　\frac{60}{11}　}}\,(\,\mathrm{cm}\,)
\end{eqnarray}\)
※
角の二等分線定理の証明は会員は知っているとは思いますが、
結果だけを利用しても良いですよ。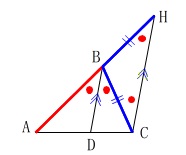\(\begin{eqnarray}
\mathrm{AB:BC}&=&\mathrm{AB:BH}\\
&=&\mathrm{AD:DC}
\end{eqnarray}\)
補助線引ければ簡単でしょう？

⑥-(2)②（別解）ひし形を利用した相似比利用の方法

本来ならこの別解を先に説明するべきですが、
三重県に限らず角の二等分線は割と出題されるのでこちらを別解とします。

直線\(\,\mathrm{BG}\,\)に平行な直線\(\,\mathrm{DK}\,\)を引くと、
四角形\(\,\mathrm{BGDK}\,\)はひし形になります。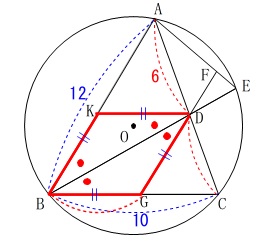求める線分\(\,\mathrm{DG}\,\)の長さを\(\,a\,\)とすると,
\(\hspace{10pt}\mathrm{DG=BG=DK=BK}=\color{red}{a}\)
\(\hspace{10pt}\mathrm{AK}=\color{red}{12-a}\)
\(\hspace{10pt}\mathrm{CG}=\color{red}{10-a}\)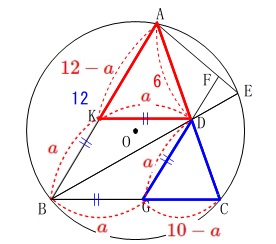\(\,\mathrm{△AKD}\,\)∽\(\,\mathrm{△DGC}\,\)なので
　\(\begin{eqnarray}
\mathrm{AK:KD}&=&\mathrm{DG:GC}\\
(12-a):a&=&a:(10-a)\\
a^2&=&(12-a)(10-a)\\
a^2&=&a^2-22a+120\\
22a&=&120\\
a&=&\frac{120}{22}\\
&=&\underline{\underline{　\frac{60}{11}　}}\,(\,\mathrm{cm}\,)
\end{eqnarray}\)
２次方程式？と思わせて１次方程式なのが良いですね。

ちなみに先の定理利用の方法だと計算は数秒です。
\(\hspace{10pt}\displaystyle 12\times \frac{5}{11}=\frac{60}{11}\)

第７問空間図形

\(\large{\color{black}{\fbox{7}}}\)
立体（円すい）の体積と線分の長さを求めます。
※
長さの単位は\(\,\mathrm{cm}\,\)です。
(1)
体積なので高さが必要です。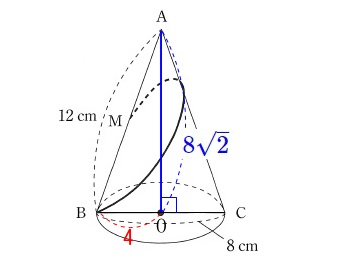底面の円の半径は\(\,\color{red}{4}\,\)なので高さは三平方の定理から
　\(\begin{eqnarray}
\mathrm{AO^2+BO^2}&=&\mathrm{AB^2}\\
\mathrm{AO^2}+4^2&=&12^2\\
\mathrm{AO^2}&=&128\\
\mathrm{AO}&=&\pm 8\sqrt{2}
\end{eqnarray}\)
長さだから
\(\hspace{10pt}\mathrm{AO}=\color{blue}{8\sqrt{2}}\)

求める円すいの体積Vは
　\(\begin{eqnarray}
V&=&\frac{1}{3}\times \pi\,(\,\color{red}{4}\,)^2\times \color{blue}{8\sqrt{2}}\\
&=&\underline{\underline{　\frac{128\sqrt{2}}{3}\,\pi\,　}}(\,\mathrm{cm^3}\,)
\end{eqnarray}\)

(2)
「最も短くなる」長さを求めるので直線です。
立体のまま考えるのではなくて展開図で直線です。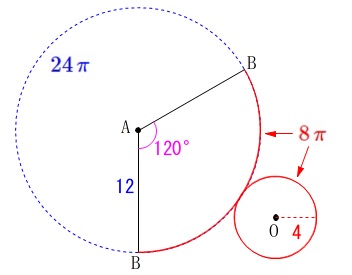底面の円周は\(\,\color{red}{8\,\pi}\,\)なので、
側面のおうぎ形の弧も\(\,\color{red}{8\,\pi}\,\)です。
母線の\(\,\color{blue}{12}\,\)を半径とする円周は\(\,\color{blue}{24\,\pi}\,\)なので、
おうぎ形の中心角は
\(\hspace{10pt}\displaystyle 360°\times \frac{8\,\pi}{24\,\pi}=\color{magenta}{120°}\)
となっています。

点\(\,\mathrm{M}\,\)は\(\,\mathrm{AB}\,\)の中点なので、
点\(\,\mathrm{B}\,\)と直線でつなぎます。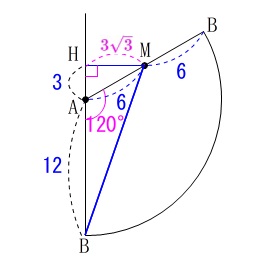線分\(\,\mathrm{BM}\,\)が求める長さです。

点\(\,\mathrm{M}\,\)から直線\(\,\mathrm{AB}\,\)に垂線を下ろして交点を\(\,\mathrm{H}\,\)とすると、
三角定規ができるので
\(\hspace{10pt}\mathrm{AH}=\color{blue}{3}\,,\,\mathrm{MH}=\color{magenta}{3\sqrt{3}}\)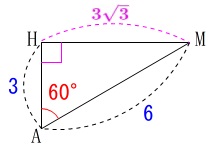\(\,\mathrm{△BHM}\,\)において三平方の定理から
　\(\begin{eqnarray}
\mathrm{BM^2}&=&\mathrm{BH^2+HM^2}\\
&=&(3+12)^2+(3\sqrt{3})^2\\
&=&225+27\\
&=&252\\
\mathrm{BM}&=&\pm 6\sqrt{7}
\end{eqnarray}\)
長さなので正の数だから
\(\hspace{10pt}\mathrm{BM}=\underline{　6\sqrt{7}　}\,(\,\mathrm{cm}\,)\)

この問題も対策を質問してくれた人は迷わず方針が立ったと思います。
計算ミスは、分かりません。

もう一手間かかる問題が神奈川県で同年に出されていました。

⇒　2023年（令和5年）度神奈川県公立高校入試数学の問題と解説

問\(\,6\,\)ですがどちらも考え方は同じです。

終わりですね、以上です。

⇒　三重県公立高校入試の数学の問題と解説

繰り返します。
三重県の公立入試では前期後期ともハチャメチャな難問は出てきません。
簡単とも言えませんが基本重視の応用を利かせた良い問題が並びます。