2023年(令和5年)度高知県公立高校入試Ａ日程の数学の問題と解説

2023年(令和5年)度高知県公立高校入試Ａ日程の数学の問題と解説です。
大問６つは昨年度と同様で、基本中心に応用を効かせるというのも変わりありません。
大問中の誘導関係はそれ程強力ではないので切替をしっかりやれば単独問題としてあつかえます。
逆に、条件をしっかり見ておかなければ全体で利用できません。

2023年(令和5年)度高知県公立高校入試Ａ日程の数学の問題

令和５年度Ａ日程高知県公立高校入試（学力検査）の数学の問題です。

⇒　令和５年度高知県公立高校入試Ａ日程の数学の問題PDF

大問は昨年度同様６つあります。

2023年(令和5年)度高知県公立高校入試Ａ日程の数学の解説

全体を通じて誘導の少ない単発問題とみてとらえることができる問題構成ですが、
条件をしっかり読み取っておかなければ方針を立てるのに苦労するかもしれません。
無駄な日本語が少ない分、シンプルに数学の基礎を広く問われますので、
どれだけ基礎を作ってきたかの差が出ると思います。

あれこれ考えず作業も含め基本的な解法でどんどん進めて見ていきましょう。

第１問小問集合

\(\color{black}{\fbox{1}}\)
(1)計算です。
①
　\(\hspace{10pt}-5+1-(-12)\\
=-5+1+12\\
=\underline{　8　}\)

（かっこ）を無くすことからですね。
②
　\(\hspace{10pt}\displaystyle \frac{3x+y)}{2}-\frac{x+y}{3}\\
\displaystyle =\frac{3(3x+y)-2(x+y)}{6}\\
\displaystyle =\frac{9x+3y-2x-2y}{6}\\
\displaystyle =\underline{\underline{　\frac{7x+y}{6}　}}\)

通分して分子の計算に集中です。
③
　\(\hspace{10pt}\displaystyle -ab^2\div \color{red}{\frac{2}{3}a^2b}\times (-4b)\\
\displaystyle =\frac{ab^2\times \color{red}{3}\times 4b}{\color{red}{2a^2b}}\\
\displaystyle =\underline{\underline{　\frac{6\,b^2}{a}　}}\)

符号の確認からですが、
割り算部分の逆数では分母分子を間違えないように注意です。
④
　\(\hspace{10pt}\displaystyle \frac{8}{\sqrt{12}}+\sqrt{50}\div \sqrt{6}\\
\displaystyle =\frac{8}{2\sqrt{3}}+\frac{5\sqrt{2}}{\sqrt{6}}\\
\displaystyle =\frac{4}{\sqrt{3}}+\frac{5}{\sqrt{3}}\\
\displaystyle =\frac{4\sqrt{3}}{3}+\frac{5\sqrt{3}}{3}\\
\displaystyle =\frac{4\sqrt{3}+5\sqrt{3}}{3}\\
\displaystyle =\frac{9\sqrt{3}}{3}\\
\displaystyle =\underline{　3\sqrt{3}　}\)

素因数分解をていねいにしておけば３行目からは
　\(\hspace{10pt}\displaystyle \frac{4}{\sqrt{3}}+\frac{5}{\sqrt{3}}\\
\displaystyle =\frac{9}{\sqrt{3}}\\
\displaystyle =\frac{9\sqrt{3}}{3}\\
\displaystyle =3\sqrt{3}\)
でも良いです。

無理数の計算では過ぎた暗算をしない方が良いですね。
（無理数計算に限った話ではありませんけど。）
(2)
平均値を求めるつもりで等式を立てれば良いだけです。

自転車通学\(\,23\,\)人の総時間は\(\,\color{red}{23\,a}\,\)分、
徒歩通学\(\,7\,\)人の総時間は\(\,\color{blue}{7\,b}\,\)分、
全体\(\,30\,\)人の平均は\(\,\color{magenta}{14}\,\)分なので、
\(\hspace{10pt}\displaystyle \frac{\color{red}{23\,a}+\color{blue}{7\,b}}{30}=\color{magenta}{14}\)

これを\(\,b\,\)について解くと
　\(\begin{eqnarray}
\frac{\color{red}{23\,a}+\color{blue}{7\,b}}{30}&=&\color{magenta}{14}\\
23\,a+7\,b&=&14\times 30\\
7\,b&=&14\times 30-23\,a\\
b&=&\frac{14\times 30-23\,a}{7}　←\,なくても良い。\\
b&=&\underline{\underline{　60-\frac{23\,a}{7}　}}
\end{eqnarray}\)

もちろん
\(\hspace{10pt}\displaystyle b=60-\frac{23}{7}\,\color{red}{a}\)
でも良いですよ。
（\(\,\color{red}{a}\,\)はしっかり分子側と見せておきましょう。）

\(\hspace{10pt}\displaystyle b=\frac{420-23\,a}{7}\)
でも良いとは思いますが、掛け算よりも約分を優先しました。
(3)
平行四辺形の成立条件の確認です。
ア
２組の対角がそれぞれ等しいので平行四辺形になります。○
イ
台形が反例としてあります。×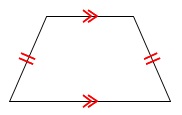
ウ
ひし形以外の四角形が反例になります。×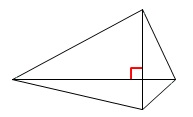
エ
平行四辺形の定理の１つです。
逆もなり立ちます。○

答え\(\hspace{10pt}\underline{　ア\,,\,エ　}\)

平行四辺形の成立条件は５つあります。
（会員は『覚え太郎』図形編\(\,\mathrm{No.45}\,\)で確認しておきましょう。）
(4)
因数分解です。
手順通りやれば公式１つ利用で終わりです。
　\(\hspace{10pt}8a^2b-18b\\
=2b\,(\,4a^2-9\,)\\
=2b\,\{\,(\,2a\,)^2-(\,3\,)^2\}\\
=\underline{　2b(2a+3)(2a-3)　}\)

第１の手順となる共通因数を抜き出せば、
後は気がつくでしょう。

⇒　中学3年の因数分解公式まとめと典型的な応用問題の解き方

展開は地道にやれば必ずできますが、
因数分解の公式が必要無いということはありません。
(5)
「交点」を通るという条件です。

連立方程式
　\( \begin{cases}
\hspace{4pt} 3x+2y+16=0\\
\hspace{4pt} 2x-y+6=0
\end{cases}\)
を解いて\(\,x=-4\,,\,y=-2\,\)が交点の座標です。

これをもう一つの方程式に代入して、
　\(\begin{eqnarray}
a\,(-4)+(-2)+10&=&0\\
-4a&=&-8\\
a&=&\underline{　2　}
\end{eqnarray}\)

１次関数に限らず「交点」は連立方程式で求めます。
(6)
ねじれの位置です。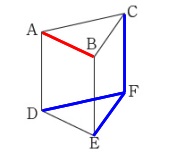平行でもなく、交わりもしない辺を選びます。

答え\(\hspace{10pt}\underline{　辺\,\mathrm{CF}\,,\,辺\,\mathrm{DF}\,,\,辺\,\mathrm{EF}　}\)

⇒　空間図形の位置関係問題(平行,ねじれの位置,垂直な面,平行な面)

ねじれの位置は注意が必要ですがこの問題は引っかけもありません。
(7)
箱ひげ図を書く前にデータを順に並べましょう。
\(\hspace{10pt}2\,,\,2\,,\,\color{blue}{3}\,,\,4\,,\,\color{red}{4}\,,\,\color{red}{6}\,,\,7\,,\,\color{magenta}{8}\,,\,9\,,\,10\)

最小値、最大値おとび四分位数が分かるので箱ひげ図を書きます。
最小値：\(\,2\,\)
第１四分位数：\(\hspace{4pt}\color{blue}{3}\)
第２四分位数（中央値）：\(\hspace{4pt}\displaystyle \frac{\color{red}{4}+\color{red}{6}}{2}=5\)
第３四分位数：\(\hspace{4pt}\color{magenta}{8}\,\)
最大値：\(\,10\,\)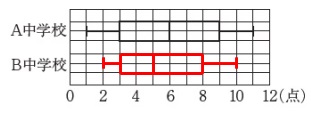箱ひげ図は四分位数の意味が分かっていればかけます。
(8)
作図です。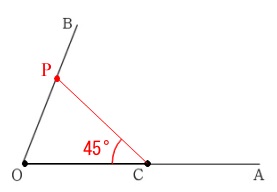点\(\,\mathrm{P}\,\)の条件は\(\,\mathrm{∠OCP=45°}\,\)となる半直線\(\,\mathrm{OB}\,\)上の点です。

\(\,45°\,\)は\(\,90°\,\)の半分なので垂線、角の二等分線、の手順で終わりです。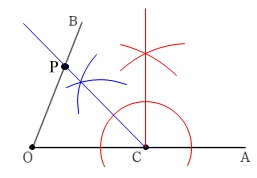作図はオリジナル問題集『さくっと！』で十分です。
※
少し難しいと感じる問題もあるかもしれませんが、
『さくっと！』の問題達に慣れれば普通の作図は即答できます。

⇒　作図問題の解き方と入試問題(角の二等分線･垂線･円の接線他)

この問題は基本問題なので手順で迷うこともないでしょう。

第２問方程式と解

\(\color{black}{\fbox{2}}\)
方程式ですが誘導というより、
解法そのまま（道幅の二通りの考え方そのもの）なので簡単に済ませます。

道幅を\(\,x\,\)とします。問題にある道は隅に寄せると分かれた畑の長方形は１つになるので、
二通りの方程式が立てられます。

道の面積を全体から引く方法と、
道を隅に寄せて畑の面積を考える方法です。
(1)
【ゆうさんのノート】では隅に寄せる方法です。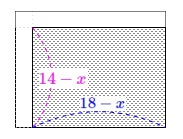畑の縦の長さと横の長さは、
それぞれ\(\,\color{magenta}{14-x}\,,\,\color{blue}{18-x}\,\)となります。

答え　\(\color{black}{\fbox{　ア　}}\,\underline{　14-x　}\,\color{black}{\fbox{　イ　}}\,\underline{　18-x　}\)
(2)
【りくさんのノート】では道の面積を引きます。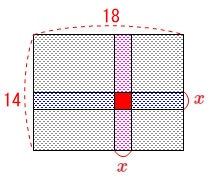縦の道の面積と横の道の面積は、
道幅が\(\,x\,\)なのでそれぞれ\(\,14\,x\,,\,18\,x\,\)となります。

答え　\(\color{black}{\fbox{　ウ　}}\,\underline{　14\,x　}\,\color{black}{\fbox{　エ　}}\,\underline{　18\,x　}\)

ただ、縦と横で道の重なる部分（\(\,\color{red}{■}\,部分\)）は２回数えているので、
１回引いておくと道の面積が出ます。
(3)
畑の面積が\(\,192\,\)となることから方程式を立てると、
(1)(2)の方法ともに整理すると
\(\hspace{10pt}\color{black}{\fbox{　\(\,x^2-32x+60\,\)　}}=0\)

これを解くと
　\(\begin{eqnarray}
x^2-32x+60&=&0\\
(x-2)(x-30)&=&0\\
x&=&2\,,\,30
\end{eqnarray}\)

土地の縦、横から道幅\(\,30\,\)ということはないので\(\,x=30\,\)は不適。
条件を満たす解は\(\hspace{10pt}x=2\)

よって道幅は\(\,\mathrm{2\,m}\,\)とすれば良い。

【ゆうさんのノート】からは
　\(\begin{eqnarray}
(14-x)(18-x)&=&192\\
x^2-32x+252&=&192\\
\color{black}{\fbox{\(　x^2-32x+60　\)}}&=&0
\end{eqnarray}\)
【りくさんのノート】からは土地から道の面積を引いて
　\(\begin{eqnarray}
14\times 18-(14x+18x-x^2)&=&192\\
252-32x+x^2&=&192\\
\color{black}{\fbox{\(　x^2-32x+60　\)}}&=&0
\end{eqnarray}\)
と、同じ方程式が出てきます。

記号の中に何を入れるかはややこしいですが、
問題としてはほんの少しの作業で片づく基本問題です。

第３問確率

\(\color{black}{\fbox{3}}\)
さいころ２つの確率なので樹形図でも表でもどちらでも良いです。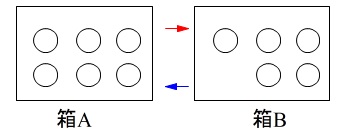さいころを投げる前は玉の個数の差は\(\,1\,\)です。
(1)
箱\(\,\mathrm{A}\,\)の個数が\(\,5\,\)個になるには、
さいころの目が一回目が二回目よりも\(\,1\,\)大きい場合です。
（箱\(\,\mathrm{A}\,\)の玉が１つ減るから）
　\(\begin{array}{|c|c|c|c|c|c|c|} \hline
& \color{red}{1} & \color{red}{2} & \color{red}{3} & \color{red}{4} & \color{red}{5} & \color{red}{6} \\ \hline
\color{blue}{\,1\,} & & ○ & & & & \\ \hline
\color{blue}{2} & & & ○ & & & \\ \hline
\color{blue}{3} & & & & ○ & & \\ \hline
\color{blue}{4} & & & & & ○ & \\ \hline
\color{blue}{5} & & & & & & ○\,\\ \hline
\color{blue}{6} & & & & & & \\ \hline
\end{array}\)

答え\(\hspace{10pt}\displaystyle \underline{\underline{　\frac{5}{36}　}}\)

ある程度樹形図を書き進めていけば、
どういう場合に箱\(\,\mathrm{A}\,\)の個数が\(\,5\,\)個になるかが見えてくると思います。
(2)
箱\(\,\mathrm{A}\,\)の玉が箱\(\,\mathrm{B}\,\)より多くなるのは、
１回目の出目が二回目以上の場合です。
（元が１個多いので戻る玉が同じかそれより多ければ良い。）
　\(\begin{array}{|c|c|c|c|c|c|c|} \hline
& \color{red}{1} & \color{red}{2} & \color{red}{3} & \color{red}{4} & \color{red}{5} & \color{red}{6} \\ \hline
\color{blue}{\,1\,} & ○ & & & & & \\ \hline
\color{blue}{2} & ○ & ○ & & & & \\ \hline
\color{blue}{3} & ○ & ○ & ○ & & & \\ \hline
\color{blue}{4} & ○ & ○ & ○ & ○ & & \\ \hline
\color{blue}{5} & ○ & ○ & ○ & ○ & ○ & \,\\ \hline
\color{blue}{6} & ○ & ○ & ○ & ○ & ○ & ○\\ \hline
\end{array}\)

答え\(\hspace{10pt}\displaystyle \frac{21}{36}=\underline{\underline{　\frac{7}{12}　}}\)

こちらも樹形図を見ていけばどういう場合かは見えてきます。
ただ、手を動かさずに考えていてもすぐには出てこないでしょう。

第４問１次関数

\(\color{black}{\fbox{4}}\)
問題文が長いですが部分的には１次関数です。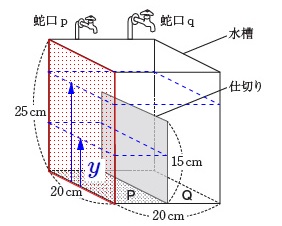水面の高さ\(\,\color{blue}{y}\,\)は面\(\,\mathrm{P}\,\)側だけを見ていることに注意です。
(1)
蛇口は\(\,p\,\)だけを開きます。
毎秒\(\,\mathrm{100\,cm^3}\,\)ずつ入るので、
底面積が\(\,\mathrm{\color{blue}{200}\,cm^2}\,\)だから\(\,2\,\)秒で\(\,\mathrm{1\,cm}\,\)水面は上がります。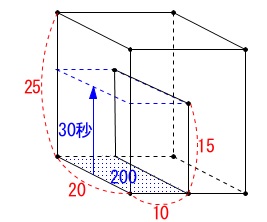仕切りの高さまでは\(\,\mathrm{15\,cm}\,\)だから\(\,30\,\)秒、
その後は\(\,\mathrm{Q}\,\)側に水は貯まっていきますが\(\,y\,\)は変わりません。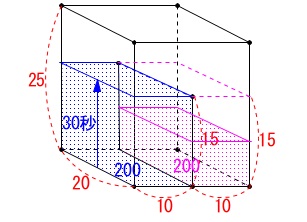
底面\(\,\mathrm{Q}\,\)側をいっぱいにする\(\,30\,\)秒かかるのでその間\(\,y\,\)は一定です。
（底面積は底面\(\,\mathrm{P}\,\)と同じ。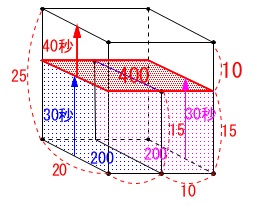）その後は底面積は\(\,\mathrm{\color{red}{400}\,cm^2}\,\)となり、
水面の高さは\(\,4\,\)秒で\(\,\mathrm{1\,cm}\,\)上昇するので、
水槽がいっぱいになるまで\(\,40\,\)秒かかります。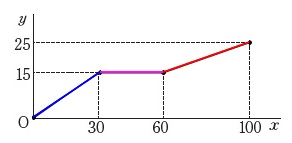
答え\(\hspace{10pt}\underline{　イ　}\)

\(\,y\,\)がどこの高さか分かれば、
傾きが\(\,30\,\)秒までより\(\,60\,\)秒後の方が小さくなることからグラフは選べます。
(2)
今度は蛇口\(\,p\,,\,q\,\)ともに開きます。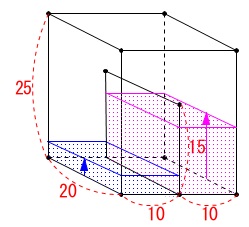蛇口\(\,q\,\)の方が毎秒\(\,\mathrm{300\,cm^3}\,\)で、
蛇口\(\,p\,\)の\(\,\mathrm{100\,cm^3}\,\)よりも大きいので、
底面\(\,\mathrm{Q}\,\)の方が先に仕切りを越えることをイメージしておきましょう。

底面\(\,\mathrm{Q}\,\)側で仕切りを超えるまで
\(\hspace{10pt}\displaystyle \frac{20\times 10\times 15}{300}=10\,秒\)
なので\(\,0\,\)秒から\(\,10\,\)秒までは\(\,y\,\)は蛇口\(\,p\,\)だけの上昇です。
このときの変化の割合は\(\,10\,\)秒で\(\,\mathrm{5\,cm}\,\)上昇するので
（\(\,x\,\)の増加量が\(\,10\,\)，\(\,y\,\)の増加量が\(\,5\,\)です。）
\(\hspace{10pt}\displaystyle \color{blue}{a}=\frac{5}{10}=\color{blue}{\frac{1}{2}}\)

その後\(\,\mathrm{Q}\,\)面側からあふれた蛇口\(\,q\,\)からの水が加わります。
\(\,10\,\)秒までで\(\,\mathrm{P}\,\)面側は\(\,\mathrm{5\,cm}\,\)上昇しているので仕切りの高さまで\(\,\mathrm{10\,cm}\,\)あり、
体積では\(\,200\times 10=2000\,\mathrm{cm^3}\)です。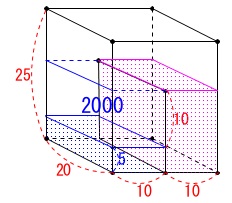このとき\(\,p\,,\,q\,\)の両方分で毎秒\(\,\mathrm{400\,cm^3}\,\)水は増えるので、
仕切りの高さまでは
\(\hspace{10pt}\displaystyle \frac{2000}{400}=5\,秒\)
なので\(\,x=10\,\)から\(\,x=15\,\)までの変化の割合は、
高さが\(\,\mathrm{10\,cm}\,\)上昇するので\(\,y\,\)の増加量が\(\,10\,\)だから
\(\hspace{10pt}\displaystyle \color{magenta}{b}=\frac{10}{5}=\color{magenta}{2}\)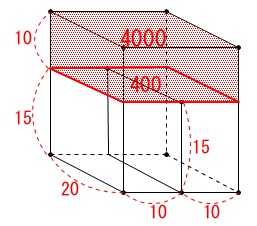仕切りを越えてからは毎秒\(\,\mathrm{400\,cm^3}\,\)で\(\,\mathrm{4000\,cm^3}\,\)を埋めていくので、
\(\,10\,\)秒間で\(\,\mathrm{10\,cm}\,\)上昇することになります。
\(\hspace{10pt}\displaystyle \color{red}{c}=\frac{10}{10}=\color{red}{1}\)

答え\(\hspace{10pt}\underline{　a\,＜\,c\,＜\,b　}\)

ここまで問題に与えられた\(\,x\,\)の区間を考えました。

仕切りを超えるまでの時間を考えないのであれば、
（問題の条件の時間\(\,x=10\,,\,15\,\)で仕切りを越えるとみる、）
変化の割合が毎秒何\(\,\mathrm{cm}\,\)の上昇かを考えて
蛇口\(\,p\,\)だけのとき底面積が\(\,200\,\)だから
\(\hspace{10pt}\displaystyle a=\frac{100}{200}=\frac{1}{2}\)
蛇口\(\,p\,,\,q\,\)のとき仕切りまでは底面積\(\,200\,\)だから
\(\hspace{10pt}\displaystyle b=\frac{400}{200}=2\)
仕切りを越えたら底面積\(\,400\,\)だから
\(\hspace{10pt}\displaystyle c=\frac{400}{400}=1\)
と\(\,a\,,\,b\,,\,c\,\)の大小は分かり易いです。
\(\hspace{10pt}\underline{　b\,＞\,c\,＞\,a　}\)

第５問関数総合

\(\color{black}{\fbox{5}}\)
関数総合問題です。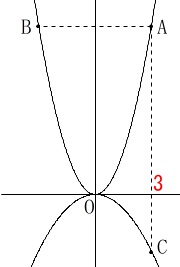関数①：\(\hspace{4pt}\displaystyle y=x^2\)
関数②：\(\hspace{4pt}\displaystyle y=-\frac{1}{3}\,x^2\)
点\(\,\mathrm{A}\,\)は\(\,x\,\)座標が\(\,\color{red}{3}\,\)。
点\(\,\mathrm{B}\,\)は点\(\,\mathrm{A}\,\)と\(\,y\,\)軸について対称（\(\,y\,\)座標が同じ）。
点\(\,\mathrm{C}\,\)は点\(\,\mathrm{A}\,\)と\(\,x\,\)座標が同じで\(\,\color{red}{3}\,\)。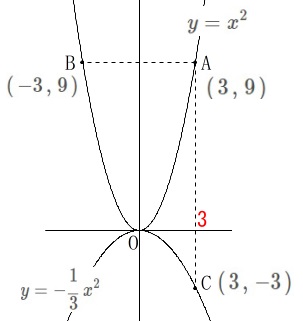３点\(\,\mathrm{A\,,\,B\,,\,C}\,\)は具体的な数値で座標が分かります。
\(\hspace{4pt}\mathrm{A}\,(\,3\,,\,9\,)\,,\,\mathrm{B}\,(\,-3\,,\,9\,)\,,\,\mathrm{C}\,(\,3\,,\,-3\,)\)
(1)
点\(\,\mathrm{C}\,\)の座標は点\(\,\mathrm{A}\,\)と\(\,x\,\)座標が同じ\(\,\color{red}{3}\,\)で関数②上の点だから、
\(\,y\,\)座標は\(\displaystyle \,y=-\frac{1}{3}\times (\,\color{red}{3}\,)^2=-3\,\)になります。

答え\(\hspace{4pt}\underline{　(\,3\,,\,-3\,)　}\)
(2)
直線\(\,\mathrm{BC}\,\)の傾き\(\,\color{blue}{a}\,\)は
\(\hspace{4pt}\mathrm{B}\,(\,-3\,,\,9\,)\,,\,\mathrm{C}\,(\,3\,,\,-3\,)\)
から
　\(\begin{eqnarray}
\color{blue}{a}&=&\frac{-3-9}{3-(-3)}\\
&=&\frac{-12}{6}=\color{blue}{-2}
\end{eqnarray}\)
点\(\,\mathrm{A}\,(\,3\,,\,9\,)\,\)を通り傾き\(\,\color{blue}{-2}\,\)の直線は
\(\hspace{10pt}y=-2\,x+15\)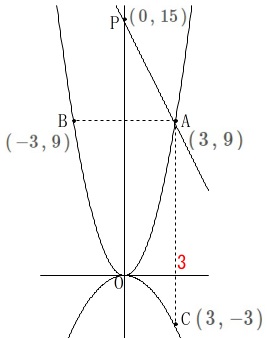これと\(\,y\,\)軸との交点\(\,\mathrm{P}\,\)の座標は
\(\hspace{10pt}\mathrm{P}\,(\,0\,,\,15\,)\)

会員は計算だけで終わらせて良いですよ。
\(\hspace{10pt}\mathrm{△PBC}=\underline{　36　}\)

一応説明しておきます。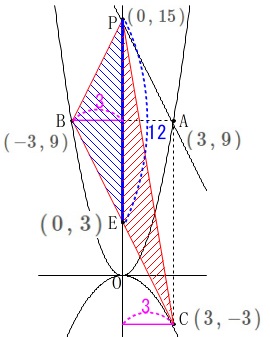直線\(\,\mathrm{BC}\,\)は\(\hspace{4pt}y=-2x+3\)で\(\,y\,\)軸との交点\(\,\mathrm{E}\,\)は\(\,(\,0\,,\,3\,)\)なので、
底辺\(\,\mathrm{PE}\,\)で高さが\(\,\mathrm{B}\,\)と\(\,\mathrm{C}\,\)から\(\,y\,\)軸までの距離として、
　\(\begin{eqnarray}
\mathrm{△PBC}&=&\mathrm{△PBE+△PCE}\\
&=&\frac{1}{2}\times \color{blue}{12}\times \color{magenta}{3}+\frac{1}{2}\times \color{blue}{12}\times \color{magenta}{3}\\
&=&\underline{　36　}
\end{eqnarray}\)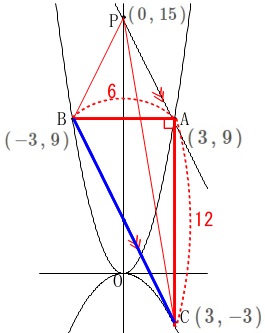直線\(\,\mathrm{BC}\,\)が直線\(\,\mathrm{AP}\,\)と平行なので、
　\(\begin{eqnarray}
\mathrm{△PBC}&=&\mathrm{△ABC}\\
&=&\frac{1}{2}\times 6\times 12\\
&=&\underline{　36　}
\end{eqnarray}\)
とする方が早いです。

問題に点\(\,\mathrm{E}\,\)の設定は(2)ではないので、
平行線による等積移動が問題の求めている方法でしょう。
けど、問題作成者の意図とか考える必要はありません。
分かることを求めにいけばいい。
(3)
これは円錐から円錐を引けば良いので簡単に済ませます。線分\(\,\mathrm{AD}\,\)を軸に回転させてできる立体の体積\(\,V\,\)は、
底面の半径\(\,\color{red}{12}\,\)、高さ\(\,\color{magenta}{6}\,\)の円錐から、
底面の半径\(\,\color{blue}{6}\,\)、高さ\(\,\color{blue}{3}\,\)の円錐を引けば良いので、
　\(\begin{eqnarray}
V&=&\frac{1}{3}\times \pi\,(\,\color{red}{12}\,)^2\times \color{magenta}{6}-\frac{1}{3}\times \pi\,(\,\color{blue}{6}\,)^2\times \color{blue}{3}\\
&=&288\,\pi-36\,\pi\\
&=&\underline{　252\,\pi　}
\end{eqnarray}\)

『超え太郎』になりますが公式を利用すると
　\(\begin{eqnarray}
V&=&\frac{1}{3}\,\pi\,\times 3\times (\,\color{blue}{6}^2+\color{red}{12}^2+\color{blue}{6}\times \color{red}{12})\\
&=&\pi\,(\,36+144+72\,)\\
&=&252\,\pi
\end{eqnarray}\)
となりますがこれは無理に覚えなくて良いといっているので、
円錐から円錐を引く方でガンガン計算していけばいいです。

回転させると円すい台になることはイメージできるようにはなっておきましょう。

第６問平面図形

\(\color{black}{\fbox{6}}\)
平面図形の問題で折り返しが２回の相似の証明と面積比です。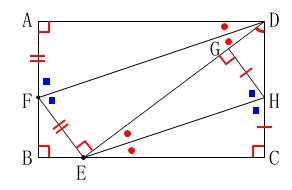折り返しが２回なので、相似がたくさんできてきます。
（合同も含めてですよ。）
※
折り返された後の角や辺は折り返す前と同じです。

面積比は相似比利用かな？と推測はしたくなります。
(1)
相似の証明です。
\(\hspace{10pt}\mathrm{△DFE}\,\)∽\(\,\mathrm{△EHG}\,\)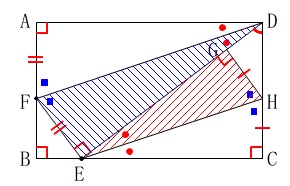折り返す前と折り返された後の角は等しいから、
図の中で証明できています。
相似条件：「２組の角がそれぞれ等しい。」

⇒　中学の図形証明問題(合同･相似)の解き方と証明の書き方ポイント

ルールを守っていれば書き方は好きにして下さい。
一応証明しておきます。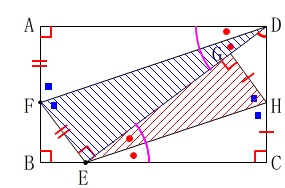（証明）
\(\hspace{10pt}\mathrm{△DFE}\,\)と\(\,\mathrm{△EHG}\,\)において、
長方形の１角が折り返されているので
　\(\hspace{10pt}\mathrm{∠FED=∠FAD}=90°　･･･①\)
　\(\hspace{10pt}\mathrm{∠HGE=∠HCE}=90°　･･･②\)
\(\,①②\,\)より
　\(\hspace{10pt}\mathrm{∠FED}=\mathrm{∠HGE}　･･･③\)
また、平行線の錯角は等しいから
　\(\hspace{10pt}\mathrm{\color{magenta}{∠ADE}}=\mathrm{\color{magenta}{∠CED}}　･･･④\)
折り返されて２等分されているから
　\(\hspace{10pt}\displaystyle \mathrm{\color{red}{∠FDE}}=\frac{1}{2}\,\mathrm{\color{magenta}{∠ADE}}　･･･⑤\)
　\(\hspace{10pt}\displaystyle \mathrm{\color{red}{∠HEG}}=\frac{1}{2}\,\mathrm{\color{magenta}{∠CED}}　･･･⑥\)
\(\,⑤⑥\,\)から等しい角をそれぞれ２等分されているから
　\(\hspace{10pt}\mathrm{\color{red}{∠FDE}}=\mathrm{\color{red}{∠HEG}}　･･･⑦\)
\(\,③⑦\,\)より、
　２組の角がそれぞれ等しい。
よって、
\(\hspace{10pt}\mathrm{△DFE}\,\)∽\(\,\mathrm{△EHG}\,\)（終わり）

図で示しているように他にも等しい角はあるので、
証明はいろいろあって良いですね。
（辺の情報はないので相似条件は限られます。）
(2)
辺の長さが加わります。
\(\hspace{10pt}\mathrm{AB}=9\,,\,\mathrm{BC}=15\)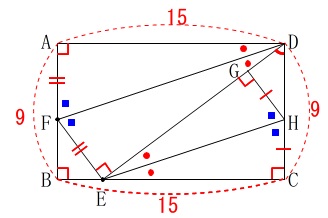※長さの単位は\(\,\mathrm{cm}\,\)です。

このとき\(\,\mathrm{\color{red}{△DFE}}\,\)の面積は\(\,\mathrm{\color{blue}{△DHG}}\,\)の面積の何倍か？です。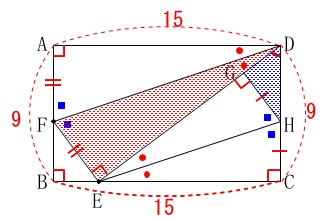相似比も出ていないので分かる長さを求めておきます。

折り返されているので
\(\hspace{10pt}\mathrm{AD=ED}=\color{red}{15}\)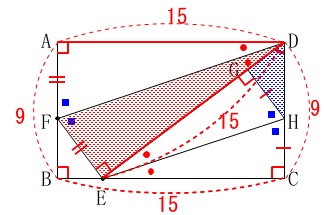ここで\(\,\mathrm{△DCE}\,\)に三平方の定理を利用して
　\(\begin{eqnarray}
\mathrm{DE^2}&=&\mathrm{DC^2+EC^2}\\
15^2&=&9^2+\mathrm{EC^2}\\
\mathrm{EC^2}&=&225-81\\
&=&144\\
\mathrm{EC}&=&\pm 12
\end{eqnarray}\)
長さだから
\(\hspace{10pt}\mathrm{EC}=\color{blue}{12}\)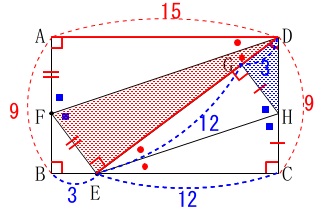このとき
\(\hspace{10pt}\mathrm{EG}=\color{blue}{12}\,,\,\mathrm{BE}=\color{blue}{3}\,,\,\mathrm{DG}=\color{blue}{3}\)
なので、ここまできれいな数値で出てくると推測したくなりますね。
（\(\,\mathrm{△DHG}\,\)が\(\,3\,,\,4\,\,,5\,\)の直角三角形じゃないか？って。）

(1)で証明した相似を利用しましょう。
\(\,\mathrm{△DFE}\,\)∽\(\,\mathrm{△EHG}\,\)で相似比は
\(\hspace{10pt}\mathrm{DE:EG}=\color{red}{15}:\color{blue}{12}=\color{magenta}{⑤}:\color{magenta}{④}\)ここまでくれば具体的な面積計算でも求まりそうです。

これは方針が分かれるでしょうね。

四角形\(\,\mathrm{FEDH}\,\)が台形なので高さが等しいから、
　\(\begin{eqnarray}
\mathrm{△DFE:△DEH}&=&\mathrm{FD:EH}\\
&=&\color{magenta}{⑤}:\color{magenta}{④}
\end{eqnarray}\)
これから
\(\hspace{10pt}\displaystyle \mathrm{\color{red}{△DEH}}=\color{red}{\frac{4}{5}\times \mathrm{△DFE}}\)
また線分\(\,\mathrm{DE}\,\)について
　\(\hspace{10pt}\mathrm{EG:GD}=12:3=4:1\)
なので\(\,\mathrm{△DHG}\,\)の面積は
　\(\begin{eqnarray}
\mathrm{△DHG}&=&\frac{1}{1+4}\times \mathrm{\color{red}{△DEH}}\\
&=&\frac{1}{5}\times \mathrm{\color{red}{△DEH}}\\
&=&\frac{1}{5}\times \color{red}{\frac{4}{5}\times \mathrm{△DFE}}\\
&=&\frac{4}{25}\times \mathrm{△DFE}
\end{eqnarray}\)
よって、
　\(\begin{eqnarray}
\mathrm{△DFE}&=&\frac{25}{4}\times \mathrm{△DHG}
\end{eqnarray}\)

答え\(\hspace{10pt}\displaystyle \underline{\underline{　\frac{25}{4}　}}\,倍\)

比だけで進めるとなんとなくしっくりこないと思うので、
具体的な長さを求めて面積計算しておきます。

相似比から
\(\hspace{10pt}\mathrm{AF=EF}=5x\,,\,\mathrm{CH=GH}=4x\)
とすると
\(\hspace{10pt}\mathrm{FB}=9-5x\,,\,\mathrm{DH}=9-4x\)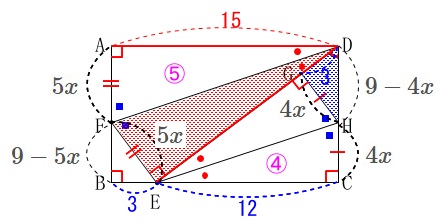直角三角形を適当に選んで三平方の定理を利用すると、
\(\hspace{10pt}x=1\)
となるので、
\(\hspace{10pt}\mathrm{AF=5\,,\,FB=4\,,\,DH=5\,,\,CH=4}\)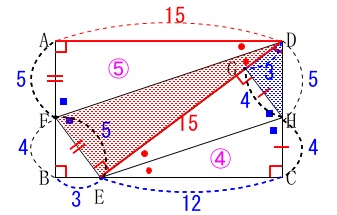これから
　\(\begin{eqnarray}
\mathrm{△DFE}&=&\frac{1}{2}\times \mathrm{DE}\times \mathrm{FE}\\
&=&\frac{1}{2}\times \color{red}{15}\times \color{blue}{5}\\
&=&\color{red}{\frac{75}{2}}
\end{eqnarray}\)
また
　\(\begin{eqnarray}
\mathrm{△DHG}&=&\frac{1}{2}\times \mathrm{DG}\times \mathrm{GH}\\
&=&\frac{1}{2}\times \color{blue}{3}\times \color{blue}{4}\\
&=&\color{blue}{6}
\end{eqnarray}\)
よって、\(\,\mathrm{△DFE}\,\)は\(\,\mathrm{△DHG}\,\)の
　\(\hspace{10pt}\displaystyle \color{red}{\frac{75}{2}}\div \color{blue}{6}\\
\displaystyle =\frac{75}{2}\times \frac{1}{6}\\
\displaystyle =\underline{\underline{　\frac{25}{4}　}}\,(\,倍\,)\)