2023年（令和5年度）和歌山県公立高校入試数学の問題と解説

２０２３年（令和５年度）和歌山県公立高校入試数学の問題と解説です。
大問４つは前年と同じで全体的な出題傾向も変わりはありません。
時間は十分足りると思うので問題の読み取りと見直しを徹底すれば高得点が狙えるでしょう。
規則性もありますが軽めなので確実に得点しておきたい問題です。

2023年（令和5年度）和歌山県公立高校入試数学の問題

和歌山県高等学校入学者選抜学力検査【数学】の問題です。

⇒　2023年（令和5年度）和歌山県公立高校入試数学の問題ＰＤＦ

問題数は少なくはありませんが、
試験時間５０分ですので十分余裕を持たせてくれていると思えます。

2023年（令和5年度）和歌山県公立高校入試数学の解説

基礎をしっかり固めておけばそれ程きびしい問題はありませんので、
解説は簡単に済ませておきます。

第１問小問集合１

\(\large{\color{black}{\fbox{1}}}\)
少し暗算を含めて計算を進めますので、
分からないところがあれば質問して下さい。
〔問１〕
計算が５つあります。
(1)
　\(\hspace{10pt}2-6\\
=\underline{　-4　}\)
(2)
　\(\hspace{10pt}\displaystyle \frac{8}{5}+\frac{7}{15}\times (-3)\\
\displaystyle =\frac{8}{5}-\frac{7}{5}\\
\displaystyle =\underline{\underline{　\frac{1}{5}　}}\)
(3)
　\(\hspace{10pt}3(2a+b)-(a+5b)\\
=6a+3b-a-5b\\
=\underline{　5a-2b　}\)

２行目は省略しない方がミスは確実に減ります。
(4)
　\(\hspace{10pt}\displaystyle \frac{9}{\sqrt{3}}-\sqrt{75}\\
\displaystyle =3\sqrt{3}-5\sqrt{3}\\
=\underline{　-2\sqrt{3}　}\)

無理数の計算は暗算の程度が人によって違うと思います。
分母の有理化、素因数分解は確実にやっておきましょう。
（２行目ですね。）
(5)
　\(\hspace{10pt}a(a+2)+(a+1)(a-3)\\
=a^2+2a+a^2-2a-3\\
=\underline{　2a^2-3　}\)

ここまで問題用紙の余白を使って行った計算を書いておきました。
最低限だとは思いますがもっと確実にした方が良いとは思います。
逆にこれ以上暗算している人は計算にすごい自信があるのでしょうが、
そのような人の真似はしない方が良いです。
〔問２〕
因数分解します。
　\(\hspace{10pt}x^2-12x+36\\
=\underline{　(x-6)^2　}\)

定数が平方数であることに着目すると、
公式そのものです。
　\(\hspace{4pt}\color{red}{a^2-2ab+b^2=(a-b)^2}\)

⇒　中学3年の因数分解公式まとめと典型的な応用問題の解き方

高校入試で扱う因数分解の公式は少ないので覚えて使いましょう。
〔問３〕
絶対値の説明は今さら必要ないでしょうが、

⇒　正の数負の数の大小を比較する数直線利用の練習問題と絶対値の意味

０を忘れないようにしましょう。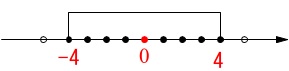\(\hspace{4pt}\pm 4\,,\,\pm 3\,,\,\pm 2\,,\,\pm 1\,,\,0\)

答え\(\underline{　9　}個\)
〔問４〕
相対度数分布表です。
度数は分かっているので表を完成させてしまえば終わりますが、
部分的に見ても解決します。
　\(\begin{array}{|c|c|c|c|} \hline
　通学時間　 &　度数　&　相対度数　&　累積度数　\\ \hline
\,0\,～\,10\, & \color{blue}{24} & 0.12 & 24 \\ \hline
\,10\,～\,20\, & \color{blue}{56} & 0.28 & 80 \\ \hline
\,20\,～\,30\, & \color{blue}{64} & 0.32 & \color{blue}{144} \\ \hline
\,30\,～\,40\, & 40 & 0.20 & 184 \\ \hline
\,40\,～\,50\, & 16 & \color{red}{0.08} & 200 \\ \hline
　計　& 200 & 1.00 & \\ \hline
\end{array}\)

答え　\(\color{black}{\fbox{　ア　}}　\underline{　0.08　}\,,\,\color{black}{\fbox{　イ　}}　\underline{　144　}\)

一応説明しておきます。
相対度数はその階級の度数を度数合計で割れば出ます。
\(\hspace{10pt}\displaystyle \frac{16}{200}=\underline{　0.08　}\)
累積度数はその階級までの度数合計なので、
\(\hspace{10pt}24+56+64=\underline{　144　}\)
〔問５〕
関数を決定します。　
\(\hspace{10pt}y=ax^2\)
比例定数を求めますが答えは関数で答えます。

\(\hspace{10pt}(\,3\,,\,-18\,)\)を通るので
　\(\begin{eqnarray}
-18&=&a\times (\,3\,)^2\\
a&=&-2
\end{eqnarray}\)

答え\(\hspace{10pt}\underline{　y=-2\,x^2　}\)
〔問６〕
中心角を求めます。

円周角も中心角も弧の長さに比例するので、
分かる角度を求めていけば答えは出ます。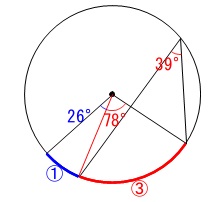簡単な計算で答えを出すなら、
弧\(\,\mathrm{BC}\,\)の円周角が\(\,39°\,\)なので中心角は\(\,\color{red}{78°}\,\)で、
弧\(\,\mathrm{AC}\,\)はその\(\displaystyle \color{blue}{\frac{4}{3}}\,\)倍だから
\(\hspace{10pt}\displaystyle \color{red}{78°}\times \color{blue}{\frac{4}{3}}=\underline{　104°　}\)

中心角を別々に求めてから足しても良いですし、
もちろん弧\(\,\mathrm{AB}\,\)の円周角を先に求めてからでも良いです。
（補助線が増えるので説明はやめておきます。）

第２問小問集合２

\(\large{\color{black}{\fbox{2}}}\)
ここも小問集合ですが少し続きがある問題です。
〔問１〕
正四角錐\(\,P\,\)の見取り図と展開図があります。
(1)
展開図と見取り図を照らし合わせます。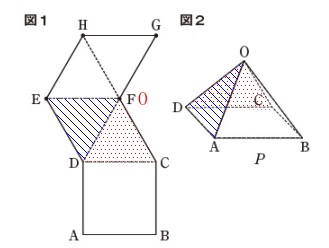線分\(\,\mathrm{DC}\,\)を１辺とする三角形は１つだから
\(\,\mathrm{△ODC}\,\)と重なるのは\(\,\mathrm{△FDC}\,\)だということは分かり易いでしょう。
つまり点\(\,\mathrm{F}\,\)が頂点\(\,\mathrm{O}\,\)です。

線分\(\,\mathrm{OD}\,\)を１辺とする三角形は\(\,\mathrm{△ODC}\,\)と\(\,\mathrm{△ODA}\,\)なので、
点\(\,\mathrm{A}\,\)と重なるのは点\(\,\mathrm{E}\,\)です。

答え　\(\,\underline{　\mathrm{E}　}\,\)
(2)
体積比を求めますが相似比から簡単に出ます。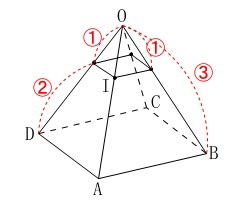相似比を\(\,1:2\,\)と間違えないようにしましょう。

相似な図形の相似比が\(\,\color{red}{a:b}\,\)のとき、
体積比は\(\,\color{blue}{a^3:b^3}\,\)になります。

四角錐\(\,Q\,\)と四角錐\(\,P\,\)（全体）は相似で相似比は\(\,\color{red}{1:3}\,\)なので、
体積比は\(\,\color{blue}{1:27}\,\)となります。なので四角錐\(\,Q\,\)と錐台\(\,R\,\)との体積比は
\(\hspace{10pt}\underline{　1:26　}\)

具体的な長さがないから相似比利用だと気はつきますが、
相似比をどこに利用するか間違えないように。
〔問２〕
簡単な規則性問題です。
どちらもあるので図で見ても表で見てもどちらでも良いです。
(1)
１３番目の色紙の色です。３の倍数のときに青色があることが分かります。
\(\hspace{10pt}13=\,3\times 4+1\)
１３番目は３の倍数の次の数なので青色の次の色です。

答え　\(\,\underline{　緑　}\,\)

説明を加えておくと３色の色紙で繰り返すので、
\(\,n\,\)を自然数とすると
緑：\(\,3n-2\,\)番目、赤：\(\,3n-1\,\)番目、青：\(\,3n\,\)番目となります。
(2)
\(\,n\,\)枚並べたときの横の長さです。
色はどうでもいいので長さだけ見ていけば良いですよ。

２の倍数ずつ増えていくのは分かるので、
\(\hspace{10pt}\color{red}{2}\,n+○\)
と推測して適当な数合わせでも答えは出ます。
※
偶数ではなく\(\,\color{red}{2}\,\)の倍数としているのは、
ずらした長さが\(\,\mathrm{2\,cm}\,\)じゃなくても通じるようにです。

色紙１枚\(\,n=1\,\)のときは長さ７なので
\(\hspace{10pt}\underline{　2n+5　}\)

\(\,n=2\,\)のときも確認すると合っています。

納得いかないでしょうから説明しておきます。
\(\,1\,\)枚のときは\(\,7\,\)でその後\(\,2\,\)ずつ増えるのですが、
\(\,2\,\)枚目から増えるので\(\,n\,\)枚のときは\(\,\color{blue}{n-1}\,\)回\(\,\color{red}{2}\,\)増えます。だから\(\,n\,\)枚のときの横の長さは
　\(\hspace{10pt}7+\color{red}{2}\,(\,\color{blue}{n-1}\,)=\underline{　2n+5　}\)
〔問３〕
さいころ２つの確率です。
図でヒントをくれていますが２つのさいころを別のさいころとして見ます。

\(\,12\,\)の約数は\(\,1\,,\,2\,,\,3\,,\,4\,,\,6\,,\,12\,\)です。
さいころ２つの出方は\(\,\color{blue}{36}\,\)通りありますが、
積が\(\,12\,\)の約数になるのは\(\,\color{red}{16}\,\)通りなので
　\(\begin{array}{|c|c|c|c|c|c|c|} \hline
& 1 & 2 & 3 & 4 & 5 & 6 \\ \hline
\,1\, & ○ & ○ & ○ & ○ & & ○\\ \hline
2 & ○ & ○ & ○ & & & ○\\ \hline
3 & ○ & ○ & & ○ & & \\ \hline
4 & ○ & & ○ & & & \\ \hline
5 & & & & & & \\ \hline
6 & ○ & ○ & & & & \\ \hline
\end{array}\)

\(\hspace{10pt}\displaystyle \frac{\color{red}{16}}{\color{blue}{36}}=\underline{\underline{　\frac{4}{9}　}}\)

もちろん樹形図でも良いです。
〔問４〕
連立方程式です。
比較はないので求めるものを文字でおいて良いですね。

ドーナツを\(\,x\,\)、カップケーキを\(\,y\,\)個作るとすると
合わせて\(\,18\,\)個作るので
\(\hspace{10pt}x+y=18　･･･①\)
小麦粉を全体で\(\,\mathrm{400\,g}\,\)使うので
\(\hspace{10pt}25x+15y=400　･･･②\)
\(\,①②\,\)を連立して
\(\hspace{10pt}x=13\,,\,y=5\)

答え　\(\,\underline{　ドーナツ\,13\,個\,,\,カップケーキ\,5\,個　}\,\)

⇒　連立方程式の問題と解き方(加減法と代入法の選び方)

連立方程式を解くときは代入法でも良いですが、
\(\,②\,\)を両辺\(\,5\,\)で割っておくと小さい数で処理できます。

「個数」と「小麦粉の量」で方程式が２つ立てられれば何でも良いです。
〔問６〕
箱ひげ図ですが四分位数は１５というデータ数が一番分かり易いです。
\(\hspace{4pt}○○○\color{blue}{●}○○○\color{red}{●}○○○\color{magenta}{●}○○○\)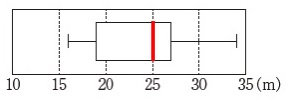箱ひげ図から中央値は\(\,\color{red}{25}\,\)なので、
データを小さい順に並べたとき、
少なくとも\(\,\color{red}{8}\,\)番目のデータは\(\,25\,\)です。
※
大きい方から見ても\(\,7\,\)番目や\(\,9\,\)番目が\(\,25\,\)でも中央値は同じです。

\(\,\mathrm{24.0\,m}\,\)は中央値より小さいから上位\(\,8\,\)番以内とはなりません。

データを順に並べたとき\(\,8\,\)番目の値が中央値となること、
中央値\(\,\color{red}{25}\,\)より値が小さいこと、
が書けていれば上位\(\,8\,\)番以内ではない理由が言えます。

平均値は四分位数とは一致するとは限らないしこの箱ひげ図では示されていません。

第３問関数

\(\large{\color{black}{\fbox{3}}}\)
関数ですが直線のみを扱います。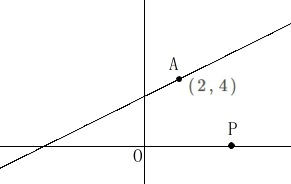点\(\,\mathrm{A}\,\)は固定されています。
\(\hspace{4pt}\mathrm{A}\,(\,2\,,\,4\,)\)
関数：\(\hspace{4pt}\displaystyle y=\frac{1}{2}\,x+3　･･･①\)

〔問１〕
変化の割合い（傾き）の問題です。
　\(\hspace{4pt}\displaystyle (\,変化の割合\,)=\frac{　(\,y\,の増加量\,)　}{　(\,x\,の増加量\,)　}\)

関数\(\,①\,\)の変化の割合（傾き）は\(\,\displaystyle \color{red}{\frac{1}{2}}\,\)なので、
\(\,x\,\)の増加量が\(\,\color{blue}{4}\,\)のとき
　\(\begin{eqnarray}
\color{red}{\frac{1}{2}}&=&\frac{　(\,y\,の増加量\,)　}{　\color{blue}{4}　}\\
(\,y\,の増加量\,)&=&\color{red}{\frac{1}{2}}\times \color{blue}{4}\,=\,\underline{　2　}
\end{eqnarray}\)
〔問２〕
直線の式を求めます。

点\(\,\mathrm{P}\,\)の\(\,x\,\)座標が\(\,6\,\)のとき\(\,x\,\)軸上の点なので
\(\hspace{10pt}\mathrm{P}\,(\,6\,,\,0\,)\)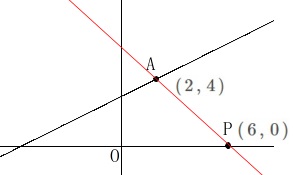直線\(\,\mathrm{AP}\,\)は２点\(\,\mathrm{A\,,\,P}\,\)を通るので
\(\hspace{10pt}\displaystyle \underline{　y=-x+6　}\)

⇒　変化の割合とは？1次関数の求め方と直線の方程式との違い

ここでは説明を省きますが１次関数は素早く求められるようになっておきましょう。
〔問３〕
点\(\,\mathrm{P}\,\)の座標を求めます。
条件：\(\hspace{10pt}\mathrm{∠APO}=30°\)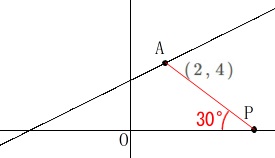座標を設定するのはやめて三角定規を利用しましょう。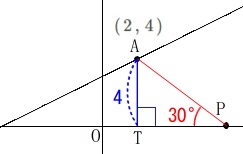点\(\,\mathrm{A}\,\)から\(\,x\,\)軸に垂線を引いて直角三角形\(\,\mathrm{APT}\,\)を作ると、
\(\,\mathrm{△APT}\,\)は三角定規になるので
\(\hspace{4pt}\mathrm{AT:PT}=1:\sqrt{3}\,\)だから
\(\hspace{10pt}\mathrm{PT}=\color{magenta}{4\sqrt{3}}\)
また\(\,\mathrm{T}\,\)の\(\,x\,\)座標は点\(\,\mathrm{A}\,\)と同じなので\(\,\mathrm{OT}=\color{red}{2}\,\)です。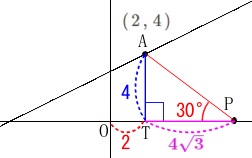よって点\(\,\mathrm{P}\,\)の\(\,x\,\)座標は
\(\hspace{10pt}\underline{　2+4\sqrt{3}　}\)
〔問４〕
２つの三角形の面積が等しくなるときです。
\(\hspace{10pt}\mathrm{△ABP}=\mathrm{△ABQ}\)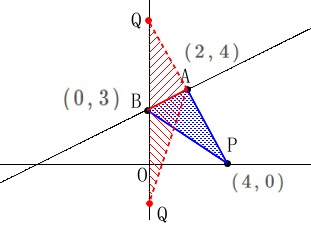点\(\,\mathrm{B}\,\)は関数\(\,①\,\)の\(\,y\,\)切片なので
\(\hspace{10pt}\mathrm{B}\,(\,0\,,\,3\,)\)
点\(\,\mathrm{P}\,\)も\(\,x\,\)座標が\(\,4\,\)の定点で
\(\hspace{10pt}\mathrm{P}\,(\,4\,,\,0\,)\)

\(\hspace{4pt}\mathrm{△ABP}\,,\,\mathrm{△ABQ}\)ともに線分\(\,\mathrm{AB}\,\)を共通にしているので、
線分\(\,\mathrm{AB}\,\)からの距離が等しい点を\(\,y\,\)軸上に探せばいいわけです。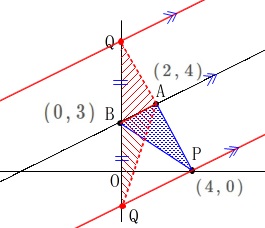点\(\,\mathrm{Q}\,\)は2つありますが、
\(\,\mathrm{△ABQ}\,\)の面積は線分\(\,\mathrm{BQ}\,\)を底辺とみると、
高さは点\(\,\mathrm{A}\,\)の\(\,x\,\)座標なので\(\,\mathrm{BQ}\,\)の長さは上と下は同じです。

上の図のように等積移動を考えると点\(\,\mathrm{P}\,\)を通り、
直線\(\,\mathrm{AB}\,\)に平行な直線の式は
\(\hspace{10pt}\displaystyle y=\frac{1}{2}\,x-2\)
なので下の点\(\,\mathrm{Q}\,\)の座標は
\(\hspace{10pt}\mathrm{Q}\,(\,0\,,\,-2\,)\)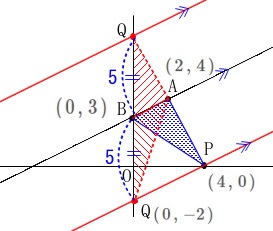このとき\(\,\mathrm{BQ=5}\,\)なので
上の点\(\,\mathrm{Q}\,\)の座標は点\(\,\mathrm{B}\,\)から\(\,y\,\)軸方向に\(\,\color{blue}{+5}\,\)だけ移動して
\(\hspace{10pt}\mathrm{Q}\,(\,0\,,\,8\,)\)

答え\(\hspace{10pt}\underline{　(\,0\,,\,2\,)\,,\,(\,0\,,\,8\,)　}\)

\(\,\mathrm{△ABP}\,\)の面積が具体的に\(\,\color{blue}{5}\,\)と求められるので、
点\(\,\mathrm{Q}\,\)を座標設定して（\(\,y\,\)座標だけで良いです。）
\(\,\mathrm{△ABQ}\,\)と等しくなるように求める事もできます。
\(\,\mathrm{△ABQ}\,\)の面積は底辺が\(\,\mathrm{BQ}\,\)で高さは点\(\,\mathrm{A}\,\)の\(\,x\,\)座標です。
（自分でやってみて下さい。）

直線\(\,\mathrm{AP}\,\)：\(\hspace{10pt}y=-2\,x+8\)
と\(\,y\,\)軸との交点を求めると\(\hspace{4pt}\mathrm{BP=BQ}\,\)となります。
※
それぞれの座標から\(\,\mathrm{AQ=AP}\,\)でもあります。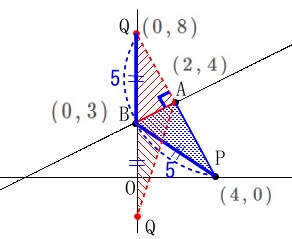直線\(\,\mathrm{AB}\,\)と直線\(\,\mathrm{AP}\,\)は垂直なので、
二等辺三角形の性質から、
\(\hspace{10pt}\mathrm{△ABP}=\mathrm{△ABQ}\)
これから上の点\(\,\mathrm{Q}\,\)が求まりますが、
あまりお勧めしません。
（直行するからやってみた、というのは良いですが「たまたま」感が強い。）

間違いではないので何でも良いですけど。

第４問平年図形

\(\large{\color{black}{\fbox{4}}}\)
平面図形（平行四辺形）総合問題です。

条件が分かり易いのでそれ程難しくは感じないでしょう。
全体を通して四角形\(\,\mathrm{ABCD}\,\)は平行四辺形です。
〔問１〕
条件は\(\,\mathrm{AB=AE}\,,\,\mathrm{∠BCD}=118°\)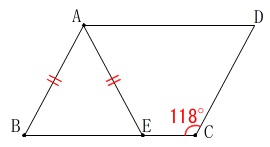平行四辺形の隣り合う角の和は\(\,180°\,\)なので
\(\hspace{10pt}\mathrm{∠ABE}=180°-\color{red}{118°}=\color{blue}{62°}\)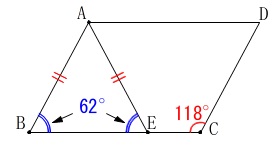二等辺三角形の底角は等しいので頂角は
　\(\begin{eqnarray}
\mathrm{∠BAE}&=&180°-2\times \color{blue}{62°}\\
&=&180^{\circ}-124^{\circ}\\
&=&\underline{　56°　}
\end{eqnarray}\)
〔問２〕
長さが出てきます。（長さの単位は\(\,\mathrm{cm}\,\)です。）
条件：\(\hspace{4pt}\mathrm{BC}=5\,,\,\mathrm{AE}=3\,,\,\mathrm{∠AEB}=90°\)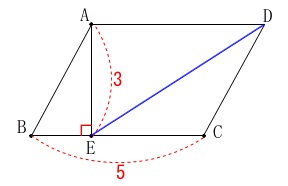このときの線分\(\,\mathrm{DE}\,\)の長さを求めます。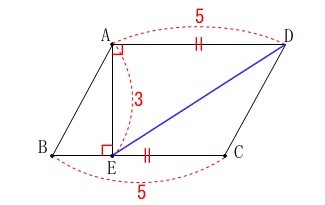\(\,\mathrm{△AED}\,\)は直角三角形で平行四辺形の対辺は等しいから、
\(\,\mathrm{AD=BC=5}\,\)なので三平方の定理から
　\(\begin{eqnarray}
\mathrm{DE^2}&=&\mathrm{AE^2+AD^2}\\
&=&3^2+5^2\\
&=&34\\
\mathrm{DE}&=&\pm \sqrt{34}
\end{eqnarray}\)
長さなので\(\,\mathrm{DE\,＞\,0}\,\)だから
\(\hspace{10pt}\mathrm{DE}=\underline{　\sqrt{34}　}(\,\mathrm{cm}\,)\)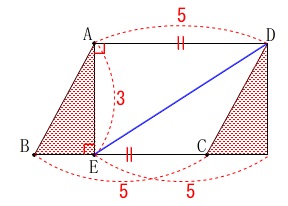平行四辺形だから\(\,\mathrm{△ABE}\,\)を右に動かすと長方形ができるので利用しても良いです。
〔問３〕
平行四辺形となることの証明です。
（平行四辺形の成立条件は５つありますので確認しておいて下さい。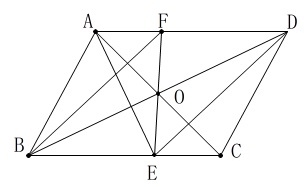）合同の証明を繰り返せばいろいろな証明ができますが、
平行四辺形の対角線はそれぞれの中点で交わることを利用するので、
合同の証明は１回で良いです。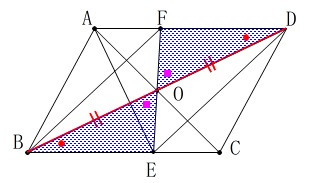平行四辺形の対角線なので
\(\hspace{10pt}\mathrm{\color{red}{OB}=\color{red}{OD}}\)
証明は省略しますが、
合同条件「１辺とその両端の角がそれぞれ等しい。」から
\(\hspace{10pt}\mathrm{△OBE}\,\)≡\(\,\mathrm{△ODF}\,\)
このことから
\(\hspace{10pt}\mathrm{\color{blue}{OE}=\color{blue}{OF}}\)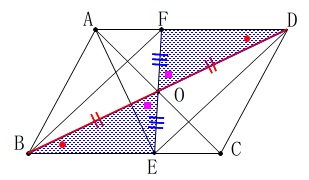これで平行四辺形の成立条件のひとつ
「対角線がそれぞれの中点で交わる。\(\,\color{red}{※①}\,\)」
または、合同が証明できたら\(\,\mathrm{BE=DF}\,\)から
「対辺が平行で等しい。」
が言えるので四角形\(\,\mathrm{BEDF}\,\)は平行四辺であることが証明できます。
（合同の証明は\(\,\color{red}{※①}\,\)をいうための条件集めです。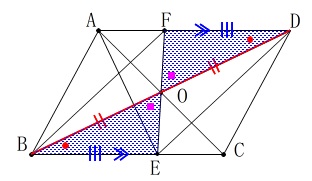）対角線が中点で交わるので\(\hspace{4pt}\mathrm{OA=OC}\)も言えるので、
合同な図形はいろいろ出てくるから他の平行四辺形の成立条件もそろえやすいと思います。
（解答にする証明の長さが変わってきますがどれでも良いです。）
〔問４〕
面積比です。
条件は問題文を読んで確認しておいて下さい。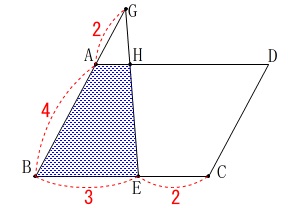台形\(\,\mathrm{ABEH}\,\)の面積と平行四辺形\(\,\mathrm{ABCD}\,\)の面積です。
これは\(\,\mathrm{△GAH}\,\)∽\(\,\mathrm{△GBE}\,\)で、
相似比が\(\,1:3\,\)が分かれば問題ないでしょう。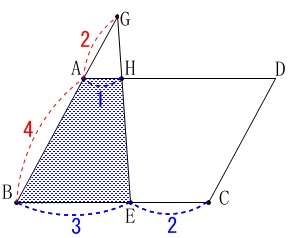方針は大きく２つに分かれると思います。

１つは台形\(\,\mathrm{HECD}\,\)を平行四辺形\(\,\mathrm{ABCD}\,\)から引く。
もう一つは直接台形\(\,\mathrm{ABEH}\,\)の面積比を求めに行く。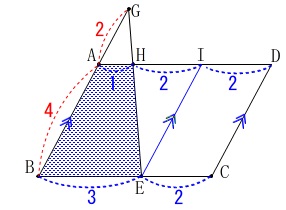点\(\,\mathrm{E}\,\)を通り\(\,\mathrm{AB}\,\)や\(\,\mathrm{DC}\,\)に平行な線を補助線として引き、
\(\,\mathrm{AD}\,\)との交点を\(\,\mathrm{I}\,\)とすると
\(\hspace{10pt}\mathrm{AH}=\color{blue}{1}\,,\,\mathrm{HI}=\color{blue}{2}\,,\,\mathrm{ID}=\color{blue}{2}\)

平行四辺形\(\,\mathrm{ABCD}\,\)の面積を\(\,S\,\)とすると、
底辺の比\(\,3:2\,\)に分割されるから
\(\hspace{4pt}\displaystyle (\,平行四辺形\,\mathrm{IECD}\,)=\color{red}{\frac{2}{5}\,S}\)
\(\,\mathrm{△EHI}\,\)の面積はその半分（底辺、高さが同じ三角形）だから
\(\hspace{4pt}\displaystyle \mathrm{△EHI}=\color{red}{\frac{1}{5}\,S}\)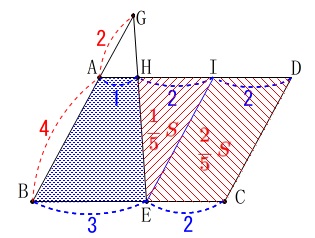よって台形\(\,\mathrm{ABEH}\,\)の面積\(\,\color{blue}{S’}\,\)は
　\(\begin{eqnarray}\displaystyle \color{blue}{S’}&=&S-\left(\color{red}{\frac{2}{5}\,S}+\color{red}{\frac{1}{5}\,S}\right)\\
\displaystyle &=&\frac{2}{5}\,S
\end{eqnarray}\)

答え\(\hspace{4pt}\displaystyle \underline{\underline{　\frac{2}{5}　}}\,(\,倍\,)\)

直接台形\(\,\mathrm{ABEH}\,\)の面積比を求めに行く場合、
線分\(\,\mathrm{AE}\,\)を引きます。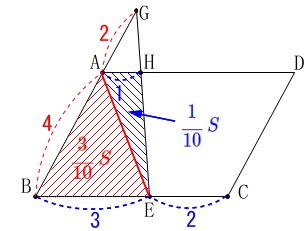平行四辺形\(\,\mathrm{ABCD}\,\)の面積を\(\,S\,\)とすると
\(\,\mathrm{△ABE}\,\)の面積は底辺を\(\,\color{blue}{3}：\color{blue}{2}\,\)に分割された\(\,\color{magenta}{三角形}\,\)だから
（ここで平行線\(\,\mathrm{EI}\,\)を考えているので上の方針が先でした。）
\(\begin{eqnarray} \mathrm{△ABE}&=&\color{magenta}{\frac{1}{2}}\times \frac{\color{blue}{3}}{\color{blue}{3}+\color{blue}{2}}\times S\\
&=&\color{red}{\frac{3}{10}\,S}
\end{eqnarray}\)
\(\,\mathrm{△AEH}\,\)は底辺が\(\,\mathrm{△ABE}\,\)の\(\,\displaystyle \frac{1}{3}\,\)で高さが同じだから
\(\begin{eqnarray} \displaystyle \mathrm{△AEH}&=&\frac{1}{3}\times \mathrm{△ABE}\\
&=&\frac{1}{3}\times \color{red}{\frac{3}{10}\,S}\\
&=&\color{blue}{\frac{1}{10}\,S}
\end{eqnarray}\)

よって台形\(\,\mathrm{ABEH}\,\)の面積\(\,S’\,\)は
　\(\begin{eqnarray}
S’&=&\color{red}{\frac{3}{10}\,S}+\color{blue}{\frac{1}{10}\,S}\\
&=&\frac{4}{10}\,S\\
&=&\frac{2}{5}\,S
\end{eqnarray}\)

平行四辺形の面積を具体的に求める事はできないので、
ここでは\(\,S\,\)としましたが\(\,①\,\)としても適当に\(\,10\,\)とでもしていいですよ。
（適当に面積を決める場合は５の倍数が楽かな、程度には慣れておくと良いです。）

簡単な解説になりましたが以上です。

⇒　和歌山県公立高校入試の数学の過去問題と解答解説

数年分見てわかると思います。
和歌山県の数学は基本重視の偏りの少ない公立高校入試らしい問題です。

会員は時間を余すと思いますので『最大得点獲得法』は試験前に必ず確認して、
満点目指して下さい。