２０２３年（令和５年度）大阪府公立高校入試の数学Ａ問題と解説です。
例年Ａ問題は教科書の基本を復習していれば高得点がとれますが、
偏りはないので教科書全体を何度も繰り返しておくことが対策となります。
特に用語はしっかり覚えておくことと、本番ではミスをできるだけ無くすように。
２０２３年（令和５年度）大阪府公立高校入試の数学Ａ問題
令和５年度の大阪府公立高校入試の数学Ａ問題です。
大問で４問あります。
大阪府の公開問題は２ページがまとまっているので分けておきました。
⇒ 令和５年度の大阪府公立高校入試の数学Ａ問題ＰＤＦ（公開分）
解答用紙も含めて公開分も載せておきます。
２０２３年（令和５年度）大阪府公立高校入試の数学Ａ問題の解説
解説は教科書通りになるので簡単に済ませます。
第１問計算問題小問集合
\(\,\large{1}\,\)
数の計算が６題あります。
(1)
\(\hspace{10pt}\color{red}{5\times (-4)}+7\\
=\color{red}{-20}+7\\
=\underline{ -13 }\)
計算順序を間違えないようにしましょう。
(2)
\(\hspace{10pt}3.4\color{red}{-(-2.5)}\\
=3.4\color{red}{+2.5}\\
=\underline{ 5.9 }\)
負の数を引くのは正の数を足すことと同じです。
二桁以上の計算は暗算せず確実に筆算した方が良いです。
(3)
\(\hspace{10pt}2\times \color{red}{4^2}\\
=2\times \color{red}{16}\\
=\underline{ 32 }\)
掛け算だけなので前からかけていっても良いです。
\(\hspace{10pt}2\times \color{red}{4^2}\\
=2\times \color{red}{4\times 4}\\
=8\times 4\\
=32\)
指数の意味が分かっていれば問題ありません。
(4)
\(\hspace{10pt}8x-3+\color{red}{2(x+1)}\\
=8x-3+\color{red}{2x+2}\\
=\underline{ 10x-1 }\)
展開して同類項をまとめるだけですが、
符号ミスが出てくるので暗算はさけておきましょう。
(5)
\(\hspace{10pt}\displaystyle -18xy\color{red}{\div 3x}\\
\displaystyle =-\frac{18xy}{\color{red}{3x}}\\
=\underline{ -6y }\)
基本通り割り算は分数計算で約分を活用します。
（『約分の効用』は無料のメルマガ会員でも会員サイトで見ることができます。）
(6)
\(\hspace{10pt}\displaystyle \sqrt{5}+\color{red}{\sqrt{45}}\\
\displaystyle =\sqrt{5}+\color{red}{3\sqrt{5}}\\
=\underline{ 4\sqrt{5} }\)
ルートの中が同じなら文字式と同じように足し算引き算できますが、
素因数分解はていねいにしておきましょう。
第２問文字式方程式等の小問集合
\(\,\large{2}\,\)
方程式や関数、図形の基本性質を問う小問が１１題あります。
(1)
\(\hspace{10pt}\displaystyle -\frac{7}{4}=-1.75\)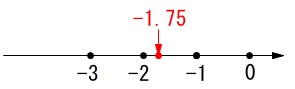
小数にして整数部分が分かれば問題ないでしょう。
答え \(\,\underline{ ウ }\,\)
(2)
これは\(\,\color{red}{a=-3}\,\)をそのまま代入して計算します。
\(\hspace{10pt}\displaystyle 4\,\color{red}{a}+21\\
=4\times \color{red}{(-3)}+21\\
=-12+21\\
=\underline{ 9 }\)
ややこしい式に代入するときは代入する式を簡単にしてから、
が基本ですがこれは直接代入するしかありません。
ただし、代入する値には（かっこ）をつけて計算するのを忘れずに。
(3)
反例を探していっても良いですが、
１つだけ選べば良いので時間を短縮できます。
\(\hspace{10pt}3\,n+6\\
=3(\,n+2\,)\)
\(\,n+2\,\)は整数なので全体は\(\,3\,\)の倍数です。
答え \(\,\underline{ エ }\,\)
⇒ 中学数学で使う文字式の一覧(奇数や偶数などの整数の表し方)
何でもそうですが、文字式は慣れる前に覚えることですね。
(4)
単なる足し算です。
重さの単位はどちらも\(\,\mathrm{g}\,\)です。
\(\hspace{10pt}\underline{ 2\,a+7\,b }\mathrm{g}\)
(5)
正五角形でも普通に五角形の内角の和は、
三角形３つ分です。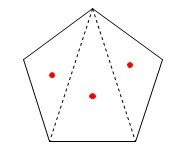
\(\hspace{10pt}\displaystyle 3\times 180^{\circ}\\
=\underline{ 540^{\circ} }\)
公式として覚えていても良いですが、
少し慣れてきたら考え方で公式が導けるようになります。
もちろん、公式を使うことが先で良いです。
「考えることが先か、公式を使えることが先か？」
公式を使えることが先で良いです。
なぜなら、球体の公式などは導けないでしょう？
『公式は導けないと意味がない。』などという自称天才達のいうことは忘れましょう。
(6)
「範囲」と「四分位範囲」の意味をここで覚えましょう。
範囲：\(\,(\,最大値\,)-(\,最小値\,)\,\)
四分位範囲：\(\,(\,第３四分位数\,)－(\,第１四分位数\,)\,\)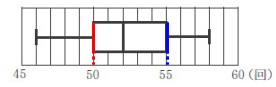
簡単に言えば「四分位範囲」は箱の幅です。
\(\hspace{10pt}\color{blue}{55}-\color{red}{50}=\,\underline{ 5 }回\)
(7)
連立方程式を解くときは一文字消去が基本です。
\( \begin{cases}
\hspace{4pt} x-3y=10 ･･･①\\
\hspace{4pt} 5x+3y=14 ･･･②
\end{cases}\)
加減法が良いですね。
\(\hspace{20pt}x-3y=10\\
\underline{\,+)\,5x+3y=14 }\\
\hspace{16pt}6x\hspace{20pt}=24\\
\hspace{42pt}x=4\)
どちらでも良いですが\(\,①\,\)に代入して
\(\begin{eqnarray}
(\,4\,)-3y&=&10\\
-3y&=&6\\
y&=&-2
\end{eqnarray}\)
答え\(\hspace{4pt}\underline{ x=4\,,\,y=-2 }\)
ここでは同じ\(\,3y\,\)があるので代入法でも良いです。
（移項して、代入して、とメンドウに感じますけどね。）
(8)
因数分解できるので解の公式は使わなくて良いです。
\(\begin{eqnarray}
x^2-2x-35&=&0\\
(x+5)(x-7)&=&0\\
x&=&\underline{ -5\,,\,7 }
\end{eqnarray}\)
左辺の因数分解は定数項\(\,35\,\)に着目して、
\(\hspace{4pt}1\times 35\,,\,5\times 7\)
後は符号を変えた組み合わせで１次の係数あわせです。
（１次の係数に合わせられない場合は解の公式。）
因数分解の公式は利用した方が計算が楽になること多いです。
(9)
さいころ二つの確率です。
樹形図で良いですが、
注意したいのは「和が\(\,10\,\)より大きい」という点ですね。
\(\begin{array}{|c|c|c|c|c|c|c|} \hline
& 1 & 2 & 3 & 4 & 5 & 6 \\ \hline
\,1\, & & & & & & \\ \hline
2 & & & & & & \\ \hline
3 & & & & & & \\ \hline
4 & & & & & & \\ \hline
5 & & & & & & ○\\ \hline
6 & & & & & ○ & ○\\ \hline
\end{array}\)
答え\(\hspace{4pt}\displaystyle \frac{3}{36}=\underline{\underline{ \frac{1}{12} }}\)
(10)
比例定数を求めます。
\(\hspace{10pt}y=a\,x^2\)
\(\,x\,\)座標は分かっているので座標を\(\,a\,\)を使って表すと、
\(\hspace{10pt}\mathrm{A}\,(\,3\,,\,\color{red}{9\,a}\,)\,,\,\mathrm{B}\,(\,-2\,,\,\color{blue}{4a}\,)\)
\(\,y\,\)座標は\(\,\mathrm{A}\,\)の方が\(\,\color{magenta}{2}\,\)大きいので
\(\begin{eqnarray}
\color{red}{9\,a}-\color{blue}{4\,a}&=&\color{magenta}{2}\\
5\,a&=&2\\
a&=&\underline{\underline{ \frac{2}{5} }}
\end{eqnarray}\)
(11)
辺\(\,\mathrm{AB}\,\)と垂直な面は２つあります。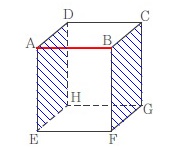
ただ、答えの選択肢には１つしかありません。
答え\(\hspace{10pt}\underline{ イ }\)（面\(\,\mathrm{BFGC}\,\)）
１つ選べばいいので全てを確認しなくても良いですが、
辺に垂直な面はイメージできるようになっておきましょう。
第３問１次関数
\(\,\large{3}\,\)
タンクの水は「一定の割合で減っていく」ので１次関数です。
初めのタンク水の量：\(\,\mathrm{840\,mL}\,\)
タンクの水の減る割合：毎分\(\,\mathrm{6\,mL}\,\)
（単位は混ざっていないので気にしなくて良いです。）
(1)
加湿器を使用した時間が\(\,x\,\)、
タンクの水の量が\(\,y\,\)で、
\(\hspace{10pt}x=0\,,\,y=840\)
①
使用した時間に比例してタンクの水は減ります。
３分で\(\hspace{4pt}6\times 3=\color{red}{18}\)
９分で\(\hspace{4pt}6\times 9=\color{blue}{54}\)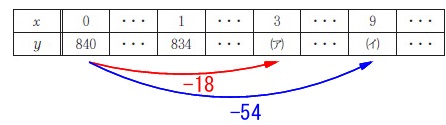
\(\hspace{10pt}840-18=\,822\)
\(\hspace{10pt}840-54=\,786\)
答え\(（ア）\underline{ 822 }\,,\,（イ）\underline{ 786 }\)
ここも暗算しないで確実に計算しましょう。
②
関数は１次関数で一定の割合で減る量\(\,\color{blue}{-6}\,\)が傾きです。
\(\hspace{10pt}y=\color{blue}{-6}\,x+b\)
\(\,y\,\)切片は\(\,\color{red}{b}\,\)最初の水の量\(\,\color{red}{840}\,\)なので
答え\(\hspace{10pt}\underline{ y=-6\,x+840 }\)
(2)
二通り考え方はあると思いますが、
使用した時間を求めるので\(\,t\,\)は\(\,x\,\)そのものです。
タンクの水の量\(\,y\,\)が\(\,450\,\)になるときなので
\(\begin{eqnarray}\displaystyle
450&=&-6\,t+840\\
6\,t&=&390\\
t&=&\underline{ 65 }
\end{eqnarray}\)
または残り\(\,450\,\)まで減った水の量を考えると
\(\hspace{10pt}840-450=390\)
毎分\(\,6\,\)で減るので
\(\hspace{10pt}\displaystyle t=\frac{390}{6}=\underline{ 65 }\)
どちらでも良いです。
第４問平面図形
\(\,\large{4}\,\)
平面図形で分かり易い条件ですが、
問題にある条件は図に書き込んでおきましょう。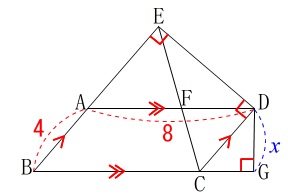
長さの単位は\(\,\mathrm{cm}\,\)です。
(1)
回転体の名称です。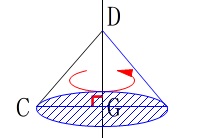
軸が\(\,\mathrm{DG}\,\)なので辺\(\,\mathrm{CG}\,\)を半径とする円が底面です。
答え\(\hspace{10pt}\,\underline{ エ }\,\)円すい
(2)
平行四辺形の面積です。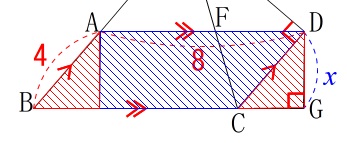
平行四辺形の面積は長方形と同じです。
（一部を移動させると長方形になるので確認。）
底辺（横）は\(\,8\,\)、高さ（縦）が\(\,x\,\)なので
答え\(\hspace{10pt}\underline{ 8x }\,\mathrm{cm^2}\)
(3)
相似の証明ですが穴埋めなので、
記号の順番を間違えないようにしましょう。
\(\hspace{10pt}\mathrm{△EAD}\,\)∽\(\,\mathrm{△GCD}\,\)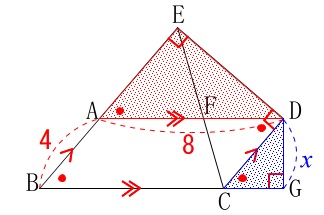
平行四辺形の対辺は平行なので、
同位角と錯角は等しいので相似条件はすぐに見つかります。
⇒ 中学の図形証明問題(合同･相似)の解き方と証明の書き方ポイント
証明は図の中で終わらせておくことです。
（証明）（一部省略）
\(\,\mathrm{△EAD}\,\)と\(\,\mathrm{△GCD}\,\)において
\(\hspace{10pt}\mathrm{DE}\,\)⊥\(\,\mathrm{EB}\,\),\(\,\mathrm{DG}\,\)⊥\(\,\mathrm{BG}\,\)だから
\(\hspace{10pt}\mathrm{∠DEA}=∠\color{black}{\fbox{\(\,\mathrm{DGC}\,\)}}=90° ･･･①\)
平行四辺形の対辺は平行で錯角は等しいから
\(\hspace{10pt}\mathrm{\color{blue}{∠EAD}}=\mathrm{\color{red}{∠ADC}}\)
また
\(\hspace{10pt}\mathrm{\color{blue}{∠\color{black}{\fbox{\(\,\mathrm{\color{blue}{GCD}}\,\)}}}}=\mathrm{\color{red}{∠ADC}}\)
だから
\(\hspace{10pt}\mathrm{\color{blue}{∠EAD}}=\mathrm{\color{blue}{∠GCD}} ･･･②\)
①②から「２組の角がそれぞれ等しい。」（\(\,\underline{ ウ }\,\)）
よって、\(\,\mathrm{△EAD}\,\)∽\(\,\mathrm{△GCD}\,\)
証明では角度しか出てきていないので相似条件は分かり易いでしょう。
自分で書く場合は記号の順番を自分で決められますが、
穴埋めではルール通りに、問題に合わせて記号の順番を入れなくてはダメです。
※
図で示しているように同位角が等しいことからも証明はできます。
(4)
線分の長さを求めます。
\(\hspace{10pt}x=\color{blue}{3}\)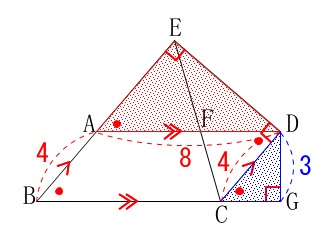
(3)の証明でしっかりとヒントをくれています。
\(\hspace{10pt}\mathrm{△EAD}\,\)∽\(\,\mathrm{△GCD}\,\)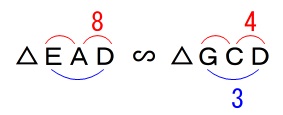
相似比から比例式を解きます。
（といってもきれいな整数比なので計算はいらないです。）
\(\begin{eqnarray}\displaystyle
\mathrm{DA:DC}&=&\mathrm{DE:DG}\\
\color{red}{8}:\color{red}{4}&=&\mathrm{DE}:\color{blue}{3}\\
4\times \mathrm{DE}&=&8\times 3\\
\mathrm{DE}&=&\color{magenta}{6}
\end{eqnarray}\)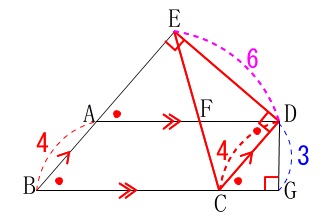
直角三角形\(\,\mathrm{EDC}\,\)に三平方の定理を使って
\(\begin{eqnarray}\displaystyle
\mathrm{EC^2}&=&\mathrm{AD^2+DC^2}\\
&=&\color{magenta}{6}^2+\color{red}{4}^2\\
&=&36+16\\
&=&52\\
\mathrm{EC}&=&\pm 2\sqrt{13}
\end{eqnarray}\)
長さなので\(\,\mathrm{EC\,＞\,0}\,\)だから
\(\hspace{10pt}\mathrm{EC}=\underline{ 2\sqrt{13} }\mathrm{cm}\)
解答には相似、三平方の定理をどこに使ったかと、
長さをしっかり示せば書き方は好きにして良いです。
他にも相似がありますが利用しにくい数値です。
なぜ直角三角形\(\,\mathrm{EDC}\,\)に着目できるかというと、
\(\hspace{10pt}\mathrm{ED}\)⊥\(\,\mathrm{DC}\,\)
という条件を使っていなかったからです。
無駄なことは問題にはないと考えていて良いですよ。
※
数学の言葉には無駄がない、ということです。
太郎さんや花子さんが相撲をした、とかは別になくてもいい。
以上です。
大阪府は\(\,\mathrm{B\,,\,C}\,\)問題もあります。
\(\,\mathrm{B\,,\,C}\,\)の解説では\(\,\mathrm{A}\,\)問題での解説は理解できているものとしていますが、
\(\,\mathrm{B}\,\)問題までは標準的な問題構成なので目を通しておくと良い対策になると思います。
※
もちろん無理はしなくて良いです。
『覚え太郎』『基礎レポート』で時間を余らせて満点狙えるのでそちらを繰り返した方が良い。
クラブ活動で忙しい！
塾に通っているのに数学が苦手！
数学の勉強時間を減らしたい！
数学の勉強方法が分からない！
その悩み、『覚え太郎』が解決します！！！
