2023年(令和5年)度三重県公立高校前期入試【数学】の問題と解説

2023年(令和5年)度三重県公立高校入試前期【数学】の問題と解説です。
大問は７問あり、ど直球に聞いてくる問題と、
ややこしく見せてシンプルなことを聞いてくる問題とあります。
それでも数学の基礎を全般的に問われますのでしっかり差はつくでしょう。

2023年(令和5年)度三重県公立高校前期入試【数学】の問題

正式名称「令和５年度三重県立高等学校入学者前期選抜学力検査問題」の数学問題です。

⇒　2023年(令和5年)度三重県公立高校前期入試【数学】の問題PDF

日本語が長くややこしい問題より、
こういう基礎を重視したシンプルな問題は得意です。笑
後半で料金問題がありますが実社会でもあることなので見ておくと良いですね。

2023年(令和5年)度三重県公立高校前期入試【数学】の解説

どうしようかな。
前年度までで解説は終わっているようなものだから、
後期で解説はしっかりするとして、
たまには私なら普段どうやって解くかを示してみましょうか。
（と言いつつ、いつもグダグダになるんですよね。）

ということで先ずは全体を見渡して、
\(\color{black}{\fbox{1}}\)から\(\color{black}{\fbox{7}}\)まであるのかあ、多いなあ、
と、よく見ると大問が多いだけで問題数はそれ程でもないか。
これは切り替えをしっかりやっていこう、という方針になる。

第１問

ここは絶対に落とさない。
(1)
符号に注意して
　\(\hspace{10pt}(-6)^2+24\div (-3)\\
=36-8\\
=\underline{　28　}\)
(2)
文字式も数字計算と同じ
　\(\hspace{10pt}4(2x-1)-6x\\
=8x-4-6x\\
=\underline{　2x-4　}\)
(3)
分数計算はいつも通り
　\(\hspace{10pt}\displaystyle 30\,a\,b\div \frac{6}{5}\,b\\
\displaystyle =\frac{30\,a\,b\times 5}{6b}\\
=\underline{　25\,a　}\)

ブツクサいいながらやっているけど、
普段は淡々と進めています。笑
(4)
無理数計算は無理して暗算しない。
　\(\hspace{10pt}\displaystyle \sqrt{18}-\frac{4}{\sqrt{8}}\\
\displaystyle =3\sqrt{2}-\frac{4}{2\sqrt{2}}\\
\displaystyle =3\sqrt{2}-\frac{4\sqrt{2}}{4}\\
\displaystyle =3\sqrt{2}-\sqrt{2}\\
\displaystyle =\underline{　2\sqrt{2}　}\)
(5)
共通因数はなし、速攻展開する。
　\(\begin{eqnarray}
x^2-3x-18&=&3x-27\\
x^2-6x+9&=&0\\
(x-3)^2&=&0\\
x&=&\underline{　3　}\, (\,重解\,)
\end{eqnarray}\)
(6)
みかんは\(\,x\,\)個で変化なし、で不等式。
５個ずつ\(\,y\,\)人に配ると足りない。
配ろうとする\(\,5y\,\)よりみかんの数\(\,x\,\)の方が少ない。
　\(\hspace{10pt}\underline{　x\,＜\,5y　}\)
(7)
変化の割合は２点を書き出す。
　\(\hspace{4pt}(\,2\,,\,4a\,)\)
　\(\hspace{4pt}(\,6\,,\,36a\,)\)
変化の割合が\(\,4\,\)だから
　\(\begin{eqnarray}
\frac{36a-4a}{6-2}&=&4\\
8a&=&4\\
a&=&\underline{\underline{　\frac{1}{2}　}}
\end{eqnarray}\)

(8)
ドストレートの質問だなあ、良い。
　\(\hspace{4pt}\displaystyle 4\,\pi\,(\,5\,)^2=\underline{　100\,\pi　}\,(\,\mathrm{cm^2}\,)\)

ここだけはちょっと言っておきます。
球に関しての問題は公式覚えていないと答えは出ませんよ。

⇒　表面積や体積の求め方(三角柱,四角柱,円柱,球や半球)

分かってはいると思いますが公式導けないでしょう？
（中学生が積分やっているならここの解説ページは見ていないでしょう。）
(9)
あ、これ方向性がいっぱい。円周角、内角の和、内対角の和と方向性がありますが、
円周角が等しいことは先ず書き込みます。後は\(\,\mathrm{△ABC}\,\)や\(\,\mathrm{△BCD}\,\)の内角の和が\(\,180°\,\)だから、
分かる角度とその円周角が等しいことから全ての角が書き込めるはずです。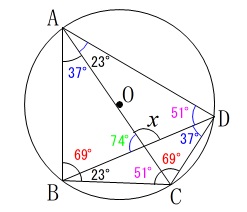円に内接する四角形の内対角が\(\,180°\,\)というのを使わないとすると、
　\(\hspace{4pt}\mathrm{∠BDC}=\color{blue}{37°}\)
\(\,\mathrm{△BCD}\,\)の内角の和が\(\,180°\,\)であることから
　\(\hspace{4pt}\mathrm{∠CBD}=23°\)
　\(\hspace{4pt}\mathrm{∠ABD}=\color{red}{69°}\)
となるので
　\(\begin{eqnarray}∠x&=&\mathrm{\color{blue}{∠BAC}+\color{red}{∠ABD}}\\
&=&\color{blue}{37°}+\color{red}{69°}\\
&=&\underline{　106°　}\end{eqnarray}\)

三角形の内角を再度利用してももちろん同じです。
どのような方向性でも良いので、
とにかく分かる角度を書き出して行くことですね。
（図に示した角度全部は必要ないです。）

(10)
作図で条件は２つ。
条件\(\,\color{red}{①}\,\)「２つの線分と距離が等しい。」⇒角の二等分線。
条件\(\,\color{blue}{②}\,\)「角度が９０°」。⇒垂線か直径に対する円周角。
で終わりですね。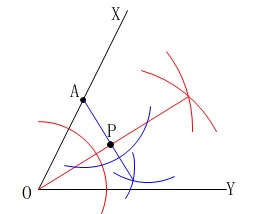条件\(\,\color{blue}{②}\,\)で円周角を利用するなら、
線分\(\,\mathrm{OA}\,\)の中点を円の中心として円を書いて交点を\(\,\mathrm{P}\,\)します。直径が\(\,\mathrm{OA}\,\)の円と、
条件\(\,\color{red}{①}\,\)を満たす角の二等分線の交点が\(\,\mathrm{P}\,\)です。
条件\(\,\color{red}{①}\,\)で書いた緑の弧を利用しても良いのですが、
わかりにくくなるので改めて垂直二等分線を書きました。

または、
点\(\,\mathrm{O}\,\)を中心、半径\(\,\mathrm{OA}\,\)とする円を書いても点\(\,\mathrm{P}\,\)は定まります。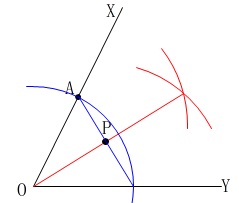条件\(\,\color{red}{①}\color{blue}{②}\,\)の順に見ていけば一番目の作図になりますが、
条件を満たしていれば何でも良い。

会員サイトの作図問題集『さくっと！』をやっている人なら迷う？くらいでしょう。

第２問

\(\color{black}{\fbox{2}}\)
度数分布表です。
(1)
たろうさんは、１年生なのでしょう。

３５人のデータの中央値は上から（下からでも同じ）１８人目になるので、
中央値が含まれる階級は
「\(\color{black}{\fbox{　20　}}\)分以上\(\color{black}{\fbox{　30　}}\)分未満の階級。」
中央値より値の大きいたろうさんは\(\color{black}{\fbox{　\(\,\mathrm{B}\,\)　}}\)チームになる。
(2)
１年生３５人の、
「３０分以４０分未満」の階級の相対度数は
　\(\hspace{4pt}\displaystyle \frac{7}{35}=0.20\)
これが２年生の同じ階級の相対度数と同じなので、
「他の階級の度数の和」\(\,\color{red}{24}\,\)が「相対度数の和」\(\,\color{blue}{0.80}\,\)になるから
２年生の生徒数（計）\(\color{black}{\fbox{　(イ)　}}\)は
　\(\hspace{4pt}\displaystyle \frac{\color{red}{24}}{\color{blue}{0.80}}=\color{black}{\fbox{　30　}}\)
※
度数の和は足し算しています。

相対度数\(\,0.20\,\)になる\(\color{black}{\fbox{　(ア)　}}\)は
　\(\hspace{4pt}\displaystyle 30\times 0.20=\underline{　6　}\)

⇒　度数分布表とは？階級の幅と階級値および累積度数とヒストグラム

度数分布表の階級値と代表値の関係は忘れないようにしましょう。

なんだかダラダラと解説していますね。
チャチャっと終わらせましょう。

第３問

\(\color{black}{\fbox{3}}\)
確率です。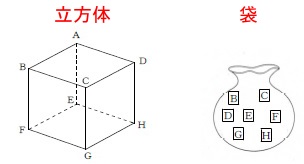(1)(2)ともに点\(\,\mathrm{A}\,\)は決まりみたいです。
(1)
袋から１枚カードを取り出します。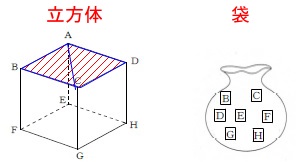できる線分が平面\(\,\mathrm{ABCD}\,\)上にあるのは、
\(\,\mathrm{B}\,\)か\(\,\mathrm{C}\,\)か\(\,\mathrm{D}\,\)を取り出したときなので
　\(\hspace{10pt}\displaystyle \underline{\underline{　\frac{3}{7}　}}\)
(2)
袋から２枚取りだし点\(\,\mathrm{A}\,\)と結ぶ。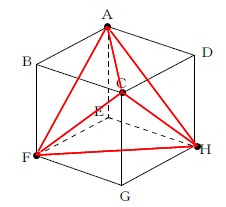点\(\,\mathrm{A}\,\)を含む三角形が正三角形になるのは、
１辺が正方形の面の対角線になるときだから、
　\(\hspace{4pt}\mathrm{C}\,,\,\mathrm{F}\,,\,\mathrm{H}\,\)
のどれか２つを取り出したとき。

取り出す順番を決めて樹形図でも良いですが組み合わせで見ると
\((\,\mathrm{B}\,,\,\mathrm{C}\,)(\,\mathrm{B}\,,\,\mathrm{D}\,)(\,\mathrm{B}\,,\,\mathrm{E}\,)(\,\mathrm{B}\,,\,\mathrm{F}\,)(\,\mathrm{B}\,,\,\mathrm{G}\,)(\,\mathrm{B}\,,\,\mathrm{H}\,)\)
\((\,\mathrm{C}\,,\,\mathrm{D}\,)(\,\mathrm{C}\,,\,\mathrm{E}\,)\color{red}{(\,\mathrm{C}\,,\,\mathrm{F}\,)}(\,\mathrm{C}\,,\,\mathrm{G}\,)\color{red}{(\,\mathrm{C}\,,\,\mathrm{H}\,)}\)
\((\,\mathrm{D}\,,\,\mathrm{E}\,)(\,\mathrm{D}\,,\,\mathrm{F}\,)(\,\mathrm{D}\,,\,\mathrm{G}\,)(\,\mathrm{D}\,,\,\mathrm{H}\,)\)
\((\,\mathrm{E}\,,\,\mathrm{F}\,)(\,\mathrm{E}\,,\,\mathrm{G}\,)(\,\mathrm{E}\,,\,\mathrm{H}\,)\)
\((\,\mathrm{F}\,,\,\mathrm{G}\,)\color{red}{(\,\mathrm{F}\,,\,\mathrm{H}\,)}\)
\((\,\mathrm{G}\,,\,\mathrm{H}\,)\)
　\(\hspace{10pt}\displaystyle \frac{3}{21}=\underline{\underline{　\frac{1}{7}　}}\)

一つ目が７個の中の当たり３つの１つ、
二つ目が残り６個の中の当たり２つの１つを取り出すので
　\(\hspace{10pt}\displaystyle \frac{3}{7}\times \frac{2}{6}=\frac{1}{7}\)
でも良いです。

注意するのは正三角形は\(\,\mathrm{△AFH}\,\)だけではない、ということでしょうか。
樹形図でも組み合わせでも書けば気がつくでしょうけど。

第４問

\(\color{black}{\fbox{4}}\)
平行四辺形です。問題にある条件はすぐに図示します。
そこから分かることを書き足しいていきます。平行四辺形は言える条件が多いので、
試験のときなら問題の順に確認して利用します。
(1)
合同の証明ですが、図中で終わっているのでまとめるだけです。
　\(\,\mathrm{△EAF}\,\)と\(\,\mathrm{△CGH}\,\)において
\(\hspace{10pt}\mathrm{EA=CG}　（仮定）･･･①\)
\(\hspace{10pt}\mathrm{\color{red}{∠AEF}=\color{red}{∠GCH}}　（平行線の錯角）･･･②\)
\(\hspace{10pt}\mathrm{\color{blue}{∠EAF}=∠CDA}　（平行線の錯角）･･･③\)
\(\hspace{10pt}\mathrm{∠CDA=\color{blue}{∠CGH}}　（平行線の同位角）･･･④\)
\(\,③④\,\)から
\(\hspace{10pt}\mathrm{\color{blue}{∠EAF}=\color{blue}{∠CGH}}･･･⑤\)
\(\,①②⑤\,\)から、
「１組の辺とその両端の角がそれぞれ等しい。」
よって、\(\,\mathrm{△EAF}\,\)≡\(\,\mathrm{△CGH}\,\)（証明終わり）

平行四辺形の対角が等しくなる事からも同じ条件が出てきますし、
三角形の内角の和が一定であることからも同じ条件が出てきます。

⇒　中学の図形証明問題(合同･相似)の解き方と証明の書き方ポイント

証明は合同条件（相似条件）さえそろえれば書き方は自分の書きやすい、
慣れている方法で良いです。
（多少回りくどくなっても構いません。）

(2)
相似比が分かり易い相似がいっぱいある。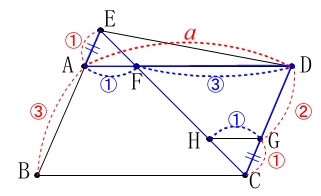(1)の合同から
　\(\hspace{10pt}\mathrm{AF=GH}\)
また、\(\,\mathrm{△AEF}\,\)∽\(\,\mathrm{△DCF}\,\)なので
（相似比\(\,1：3\,\)）
　\(\begin{eqnarray}
\mathrm{GH}&=&\mathrm{AF}\\
&=&\frac{\color{blue}{1}}{\color{blue}{1}+\color{blue}{3}}\times \mathrm{AD}\\
&=&\underline{\underline{　\frac{1}{4}\,a　}}
\end{eqnarray}\)

(3)
面積比を求めます。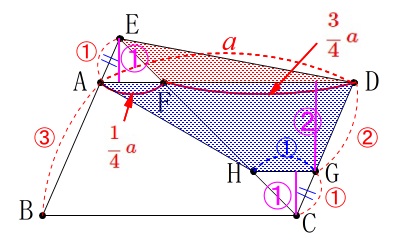基準にする面積を平行四辺形としても良いですが、
具体的な面積計算で進めます。
ただし、高さは具体的にないので比を使います。
\(\,\mathrm{△AEF}\,\)の底辺を\(\,\mathrm{AF}\,\)と見たときの高さを\(\,\color{magenta}{①}\,\)とします。

\(\,\mathrm{△EFD}\,\)の面積を\(\,S_1\,\)とすると
　\(\begin{eqnarray}
S_1&=&\frac{1}{2}\times \mathrm{FD} \times \color{magenta}{①}\\
&=&\frac{1}{2}\times \color{red}{\frac{3}{4}\,a}\times \color{magenta}{①}\\
&=&\frac{3}{8}\,a\,\times \color{magenta}{①}
\end{eqnarray}\)
「台形」\(\,\mathrm{AHGD}\,\)の面積\(\,S_2\,\)は
　\(\begin{eqnarray}
S_2&=&\frac{\color{red}{\frac{1}{4}\,a}+\,\color{red}{a}\,}{2}\times \color{magenta}{②}\\
&=&\color{red}{\frac{5}{4}\,a}\times \frac{1}{2}\times \color{magenta}{②}\\
&=&\frac{5}{8}\,a\times \color{magenta}{②}
\end{eqnarray}\)
よって求める面積比は
　\(\begin{eqnarray}
S_1:S_2&=&\frac{3}{8}\,a\times \color{magenta}{①}:\frac{5}{8}\,a\times \color{magenta}{②}\\
&=&3\times \color{magenta}{①}:5\times \color{magenta}{②}\\
&=&\underline{　3:10　}
\end{eqnarray}\)\(\,\mathrm{△AEF}\,\)を\(\,\color{red}{①}\,\)としたとき、
相似比からそれぞれの面積比が出ていれば十分です。

第５問

\(\color{black}{\fbox{5}}\)
体積と投影図です。
(1)
三角柱の体積を求めます。
普通なら長さや条件は問題から読み取っておくのですが、
問題の図に書かれてあります。底面を\(\,\mathrm{△ABC}\,\)（直角三角形）、
高さを\(\,\mathrm{AD}\,\)と見れば求める体積\(\,V\,\)は
　\(\begin{eqnarray}
V&=&\frac{1}{2}\times 4\times 4\times 6\\
&=&\underline{　48　}\,(\,\mathrm{cm^2}\,)
\end{eqnarray}\)

(2)
投影図の書き方を覚えていればすぐに終わります。

⇒　立体の見取り図と投影図と書き方と具体例の見方(中学１年空間図形)

「すべて選び」となっていますが答えだけで良いでしょう。

答え　\(\,\underline{　イ　,　エ　}\,\)

アとウではどう置いても実線や破線となるところが出てきます。

第６問

\(\color{black}{\fbox{6}}\)
連立方程式と関数ではありますが連続ではない料金問題です。
(1)
連立方程式なので求めるものを文字でおいて関係式を作ります。
（「スポーツ大会」というのは問題に関係ありません。）

「\(\,\color{red}{パンフレット１部の重さ}\,\)」を\(\,x\,\)、
「\(\,\color{blue}{箱１箱の重さ}\,\)」を\(\,y\,\)とすると、
　\( \begin{cases}
\hspace{4pt} 14\,x+y=275\\
\hspace{4pt} 31\,x+y=530
\end{cases}\)
これを解くと
　\(\hspace{10pt}\underline{　\color{red}{x}=15\,,\,\color{blue}{y}=65　}\)
単位は\(\,\mathrm{g}\,\)です。

⇒　連立方程式の問題と解き方(加減法と代入法の選び方)

解く過程は省略しています。
加減法で\(\,y\,\)を消去が早いです。

(2)
料金計算です。
（「地域フェスタ」というのは問題に関係ありません。）
①
重さを出してグラフと照らし合わせます。
チラシ\(\,30\,\)部と封筒\(\,1\,\)枚を合わせた重さは
　\(\hspace{10pt}30\times 4+16=136\,(\mathrm{g}\,)\)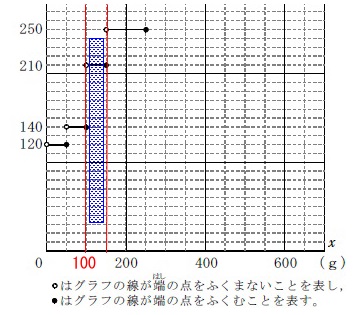\(\,136\,\)は\(\,100\,\)と\(\,150\,\)の間にある。

答え　\(\,\underline{　210　} 円\,\)

②
封筒１つの方が安い気がするかもしませんが、
現実でもそうなっていない場合があります。

ここでは最大「封筒２枚」と決まっているので、
封筒１枚のときの料金を出して比較です。

封筒１枚で全部を送ると
　\(\hspace{4pt}140\times 4+16=576\,(\,\mathrm{g}\,)\)
なので\(\,\color{red}{580}\,\)円かかります。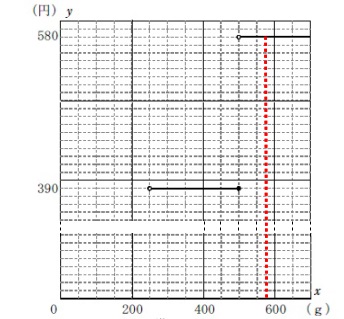封筒２枚に分けて送るとこれより安いかどうかを見ます。
例えば半分の\(\,70\,\)部ずつ封筒に入れると
　\(\hspace{4pt}70\times 4+16=296\,(\,\mathrm{g}\,)\)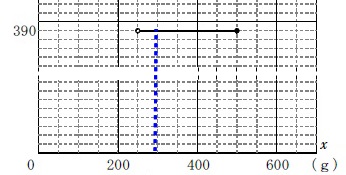１つで\(\,390\,\)円なので、
２つ分の料金は\(\,\color{blue}{780}\,\)円となり高いです。

ただし、１つの封筒には\(\,70\,\)部以上は必ず入れなくては送れない。
ということを頭においておくと、
１つは３９０円の料金で送るということになります。つまり、\(\,500\,\mathrm{g}\,\)ギリギリまでは１枚の封筒で送る方が安いということ。

１つは料金\(\,\color{red}{390}\,\)円の\(\,500\,\mathrm{g}\,\)以内にするとき、
封筒\(\,16\,\mathrm{g}\,\)を引いて送れる最大のチラシ枚数は
　\(\hspace{4pt}\displaystyle 484\div 4=121\,(\,枚\,)\)
もう１枚の封筒には残りの\(\,19\,\)枚のチラシを入れるとして、
　\(\hspace{4pt}19\times 4+16=92\,(\,\mathrm{g}\,)\)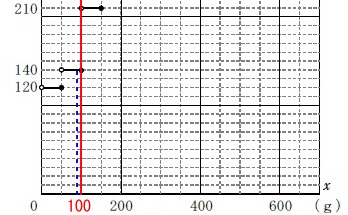この料金は\(\,\color{blue}{140}\,\)円なので、
最も安くなるときの料金は
　\(\hspace{4pt}\color{red}{390}+\color{blue}{140}=\underline{　530　}\,円\)

\(\,390\,\)円で送れる枚数を減らすと、
高くなることはあっても安くなることはない。

問題には関係ない「スポーツ大会」「地域フェスタ」という言葉が繰り返し使われています。
これ、どういう意味か分かりますよね。

第７問

\(\color{black}{\fbox{7}}\)
これはシンプルな関数問題です。直線が３本で２つが固定されている。
　\(\hspace{4pt}\displaystyle y=\frac{1}{2}\,x+b　･･･㋐\)
　\(\hspace{4pt}\displaystyle y=-2\,x-2　･･･㋑\)
　\(\hspace{4pt}\displaystyle y=x-2　･･･㋒\)

(1)
点\(\,\mathrm{P}\,\)の\(\,x\,\)座標が固定された場合の問題です。
①
点\(\,\mathrm{P}\,\)は\(\,㋑\,\)上の点なので\(\,x=-2\,\)のとき
\(\hspace{10pt}\,\mathrm{P}\,(\,-2\,,\,2\,)\)
これが\(\,㋐\,\)上の点でもあるので
　\(\begin{eqnarray}
2&=&\frac{1}{2}\times (-2)+b\\
b&=&\underline{　3　}
\end{eqnarray}\)

これで(1)の中では\(\,㋐\,\)は固定された。
\(\hspace{10pt}\displaystyle y=\frac{1}{2}\,x+3　･･･㋐\)
②
点\(\,\mathrm{R}\,\)は\(\,㋐\,\)と\(\,㋒\,\)の「交点」なので連立します。
　\(\begin{eqnarray}
\frac{1}{2}\,x+3&=&x-2\\
x+6&=&2x-4\\
x&=&10
\end{eqnarray}\)
このとき\(\,y\,\)座標は\(\,y=8\,\)となるので
　\(\hspace{4pt}\mathrm{R}\,\underline{　(\,10\,,\,8\,)　}\)

③
三角形の面積を２等分する直線です。

⇒　三角形の面積を直線が二等分する2つのパターン

図形の面積を２等分するのはいろいろ方法はありますが、
この問は具体的な面積を出しやすい形なので割と楽。三角形の面積を具体的に求めると、
（底辺は\(\,\mathrm{SQ}\,\)、高さはそれぞれの\(\,x\,\)座標と見ます。）
　\(\begin{eqnarray}
\mathrm{△PQS}&=&\frac{1}{2}\times \mathrm{SQ}\times 2\\
&=&\frac{1}{2}\times 5\times 2\\
&=&\color{red}{5}
\end{eqnarray}\)
　\(\begin{eqnarray}
\mathrm{△QRS}&=&\frac{1}{2}\times \mathrm{SQ}\times 10\\
&=&\frac{1}{2}\times 5\times 10\\
&=&\color{blue}{25}
\end{eqnarray}\)
合わせると\(\,\mathrm{△PQR}\,\)の面積は（必要無いけど）
　\(\begin{eqnarray}
\mathrm{△PQR}&=&\mathrm{△PQS+△QRS}\\
&=&\color{red}{5}+\color{blue}{25}\\
&=&30
\end{eqnarray}\)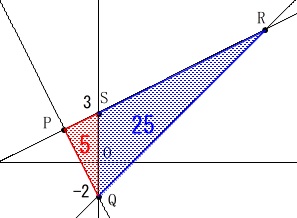２等分すると\(\,15\,\)です。

\(\,\mathrm{△PQR}\,\)の\(\,30\,\)を２等分することを考えるか、
\(\,\mathrm{△PQS}\,\)に\(\,10\,\)を加えることを考えるか、
後者ですね。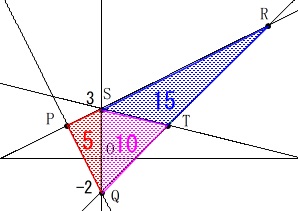図の\(\,\mathrm{△STQ}\,\)の面積が\(\,10\,\)となれば良い。
つまり、点\(\,\mathrm{T}\,\)の\(\,x\,\)座標が\(\,4\,\)となれば、
底辺\(\,\mathrm{SQ}\,\)が\(\,\color{red}{5}\,\)なので面積は２等分されます。
（\(\,\mathrm{△QRS}\,\)を\(\,2:3\,\)に分けることから\(\,\mathrm{QR}\,\)を分けて。）交点\(\,\mathrm{T}\,\)は\(\,㋒\,\)上の点なので
　\(\hspace{10pt}\mathrm{T}\,(\,4\,,\,2\,)\)
点\(\,\mathrm{S}\,\)は直線\(\,㋐\,\)の\(\,y\,\)切片で
　\(\hspace{10pt}\mathrm{S}\,(\,0\,,\,3\,)\)
この２点を通る直線は
　\(\hspace{10pt}\displaystyle \underline{\underline{　y=-\frac{1}{4}\,x+3　}}\)

⇒　1次関数の交点の座標とグラフから直線の方程式を求める方法

２点を通る直線は求められるようになっておくことが必須です。

(2)
次は\(\,㋐\,\)の\(\,b\,\)は(1)と変わっています。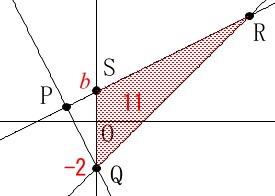点\(\,\mathrm{R}\,\)の\(\,x\,\)座標を高さとできるので、
\(\,㋐\,\)と\(\,㋒\,\)を連立して点\(\,\mathrm{R}\,\)の\(\,x\,\)座標求めると
　\(\begin{eqnarray}
\frac{1}{2}\,x+b&=&x-2\\
x+2b&=&2x-4\\
x&=&\color{blue}{2b+4}
\end{eqnarray}\)

底辺\(\,\mathrm{SQ}\,\)は\(\,y\,\)座標の差なので
　\(\hspace{10pt}\mathrm{SQ}=\color{red}{b+2}\)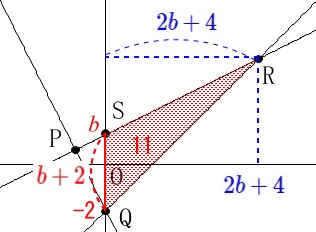\(\,\mathrm{△SQR}\,\)の面積が\(\,11\,\)のとき
　\(\begin{eqnarray}
\mathrm{△SQR}&=&11\\
\frac{1}{2}\times (\color{red}{b+2})\times (\color{blue}{2b+4)}&=&11\\
(b+2)(b+2)&=&11\\
(b+2)^2&=&11\\
b+2&=&\pm \sqrt{11}\\
b&=&-2\pm \sqrt{11}
\end{eqnarray}\)
条件が\(\,b\,＞\,0\,\)なので
　\(\hspace{10pt}b=\underline{　-2+\sqrt{11}　}\)

２次方程式の解は展開して解の公式でも良いけど、
せっかく平方完成された形で与えてくれたんだから。
（ようやく出てきた解の公式利用なので使いたい気もする。）

以上です。

なんだか解説っぽいところが多くなりました。
自分で解くと解説じみたことしないから早いけど、
（答えは『超え太郎』の範囲まで利用するから出し方違う）
問題用紙は結構汚い、というかかなり汚いくらいの作業はしていますよ。

この問題が２０分程度で一通り終わらせられるなら、
作業も含めて基礎はできていると思います。
（できないからといって焦ることもありません。）

⇒　三重県公立高校入試の数学の問題と解説

三重県の前期選抜では以前からずっと基本ガッツリの問題です。
全国的に推薦で受験するだいたいの人は過去問を参考にできますよ。