高校数学の因数分解公式には、覚える方がはやいものとそうでないものとがあります。
たすき掛け因数分解などは公式を暗記するというよりも方法を覚えることになるのでその手順が重要になります。
ここでは公式のまとめとしての確認と公式がはまらない問題への手順、やり方を説明します。
ここで説明するのは因数分解の内容ですが、中学ではやらない方法をとるものだけに集中して解説します。
中学で習う因数分解はできるものとして書きますので、忘れているようなら復習して理解しておいて下さい。
時期的には高校入学が決まった春休みや、中高一貫の中学生が高校での因数分解も同時に学習するときに、しっかり取り組んでおくといいでしょう。
もちろん遅いということはありません。
数学\(\,\mathrm{Ⅰ}\,\)の内容なので全分野で「必須」となります。
少しでも不安のある人は何度も復習しておきましょう。
因数分解の手順
先ずは、因数分解の手順を簡単にお伝えしておきます。
①共通因数をくくり出す。
②公式利用
③最低次数の文字について整理する。
④特殊な因数分解。
となります。
ほとんどの問題は③までで終わります。
④は覚えておくしかない?という気がする因数分解の方法です。
できれば、で良いので覚えておいて欲しいと思います。
①は良いでしょう。
全ての項に共通にある因数をくくり出すと言うことです。
例えば、
\(\hspace{10pt}8a^3b^4-4a^4b^3\\
=\color{red}{4a^3b^3}(2b-b)\)
の\(\, \color{red}{4a^3b^3}\,\)の部分が共通因数です。
この共通因数を抜き出すというのは、
式変形においてもまず最初にすべきことなので必ず意識しておきましょう。
次に②ですが、高校で出てくる因数分解公式は、いくつかあります。
因数分解の公式一覧
1.
\( acx^2+(ad+bc)x+bd=\color{red}{(ax+b)(cx+d)}\)
2-1.
\( a^3+b^3=\color{red}{(a+b)(a^2-ab+b^2)}\)
2-2.
\( a^3-b^3=\color{red}{(a-b)(a^2+ab+b^2)}\)
3-1.
\( a^3+3a^2b+3ab^2+b^3=\color{red}{(a+b)^3}\)
3-2.
\(a^3-3a^2b+3ab^2-b^3=\color{red}{(a-b)^3}\)
4.
\(a^2+b^2+c^2+2ab+2bc+2ca=\color{red}{(a+b+c)^2}\)
5.
\(a^3+b^3+c^3-3abc\\
=\color{red}{(a+b+c)(a^2+b^2+c^2-ab-bc-ca)}\)
証明は覚えなくて良いです。
使えるようになることが先なので証明できるできないは後回しでかまいません。
(5.の証明は最後に載せます。)
2-2.や3-2.の公式は、
2-1.や3-1.で\(\hspace{4pt} +b\hspace{4pt}\)の変わりに\(\hspace{4pt}\color{red}{-b}\hspace{4pt}\)を代入したら出てくる公式なので、
実は覚えなくても良いんですが、覚えておくと少しは時間の短縮にはなります。
例えば、3-2.は
3-1.
\( a^3+3a^2b+3ab^2+b^3=(a+b)^3\)
の\(\hspace{4pt} b\hspace{4pt}\)に\(\hspace{4pt} \color{red}{-b}\hspace{4pt}\)を代入すると、
\(\hspace{10pt} a^3+3a^2(\color{red}{-b})+3a(\color{red}{-b})^2+(\color{red}{-b})^3\\
=a^3-3a^2b+3ab^2-b^3\\
=\{a+(-b)\}^3\\
=(a-b)^3\)
となるので、2-2.も同様に覚えなくても実は使えます。
展開のときだと
\(\hspace{10pt} (a-b)^3\\ \\
=\{a+(-b)\}^3\\ \\
=a^3+3a^2(-b)+3a(-b)^2+(-b)^3\\ \\
=a^3-3a^2b+3ab^2-b^3\)
と分かり易いのですが、
展開と因数分解は両方向に変形できる必要がありますので覚えておくと見直しができますよ。
さて実用です。
因数分解公式の実用例
1.
\( acx^2+(ad+bc)x+bd=(ax+b)(cx+d)\)
は「タスキガケ因数分解」と呼ばれます。
この公式は覚えなくて良いですが、
実際に因数分解はできなくてはなりません。
例えば、
\(\hspace{10pt} 3x^2+11x+6\)
を因数分解するときを考えます。
公式通りに考えると、
\(\hspace{10pt}ac=3\,,\,ad+bc=11\,,\,bd=6\)
となり、この\(\, a\,,\,b\,,\,c\,,\,d\,\)を求めるのはやっかいです。
この公式を暗記型というには無理がありますよね。
そこで「タスキガケ」という計算作業を行います。
「\(\hspace{6pt}\color{red}{ x^2\,の係数}\hspace{6pt}\)」と「\(\color{red}{定数項}\)」
に着目します。
方程式\(\hspace{4pt} \color{red}{3}x^2+\color{magenta}{11}x+\color{blue}{6}\hspace{4pt}\)の\(\,\color{red}{3}\,\)と\(\,\color{blue}{6}\,\)です。
この\(\,\color{red}{3}\,\)と、\(\,\color{blue}{6}\,\)の約数の組み合わせでタスキガケをします。
かけて\(\,3\,\)になる数は、\(1\times 3\) だけです。
かけて\(\,6\,\)になる数は、\(1\times 6 , 2\times 3\) の二通りあります。
(それぞれの約数を組み合わせているだけです。)
\(1\times 3\,\)の1と3を縦に書き、
\(1\times 6\,\)の1と6を縦に並べて書き、
この組をクロスしてかけ、
その結果を足したり、引いたりして
\(\hspace{6pt} x\,\)の項の係数「\(\,\color{magenta}{11}\,\)」という数字を作り出せれば良いのです。
組み合わせは4通りあります。
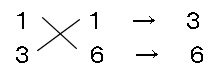
とすると3と6では足しても引いても11という数字は出てきません。
いろいろ試すと、全部で4通りありますが、
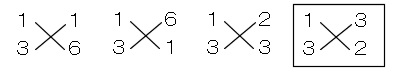
そのうち、

という組み合わせが見つかります。
この組合せを探し出すことが「自分でやるべき作業」ですが、
いくつか練習して、慣れればそれほど時間はかかりません。
ただ、自分でやらなければいつまで経ってもできるようにはなりません。
ここで、前の数字に文字を着けて( )( )とすれば良いのです。
\(\hspace{10pt} 3x^2+11x+6\\
=(x+3)(3x+2)\)
となります。
最初はめんどくさく感じますが、慣れてくるとすぐに組み合わせは見つかります。
もう一つ例題
\(\hspace{10pt} 12x^2-x-6\)
を因数分解すると
より
\(\hspace{10pt} 12x^2-x-6=(3x+2)(4x-3)\)
となります。
次は、公式2-1.2-2.です。
\( a^3+b^3=(a+b)(a^2-ab+b^2)\)
\( a^3-b^3=(a-b)(a^2+ab+b^2)\)
これらは、3次(3乗)の項と3次(3乗)の項の、和か、差、になっていれば使えます。
例
\( 8x^3+27y^3\hspace{6pt}\)は\(\hspace{4pt}(2x^3)\hspace{4pt}\)と\(\hspace{4pt}(3y)^3\hspace{4pt}\)の和になっているので、
2-1.を利用します。
\(\hspace{10pt} 8x^3+27y^3\\
=(2x+3y)\{(2x)^2-(2x)(3y)+(3y)^2\}\\
=(2x+3y)(4x^2-6xy+9y^2)\)
慣れないうちは、慣れてからもミスを減らすため、
2行目は暗算せずに書き出した方が良いですね。
次数が大きい場合は少し考えた方が楽になります。
\(\hspace{10pt} a^6-b^6\)
これは\(\hspace{4pt}a^2\hspace{4pt}\)と\(\hspace{4pt} b^2\hspace{4pt}\)の3乗になっていると考えるより、
\(\hspace{4pt} a^3\hspace{4pt}\)と\(\hspace{4pt}b^3\hspace{4pt}\)の2乗になっていると見た方が早いですね。
\(\hspace{10pt} a^6-b^6\\ \\
=\{(a^3)^2-(b^3)^2\}\\ \\
=(a^3-b^3)(a^3+b^3)\\ \\
=(a-b)(a^2+ab+b^2)(a+b)(a^2-ab+b^2)\)
中学数学で学んだ
\( a^2-b^2=(a-b)(a+b)\)
と2-1.2-2.を利用しています。
ちなみに\(\hspace{4pt}a^2\hspace{4pt}\)と\(\hspace{4pt}b^2\hspace{4pt}\)の3乗になっているとすると
\(\hspace{10pt} a^6-b^6\\
=\{(a^2)^3-(b^2)^3\}\\
=(a^2-b^2)(a^4+a^2b^2+b^4)\\
=(a-b)(a+b)\{(a^2+b^2)^2-(ab)^2\}\\
=(a-b)(a+b)(a^2+b^2-ab)(a^2+b^2+ab)\)
結果は同じですが少しレベルが上がります。
次に3-1.3-2.ですが、
これはパスカルの三角形から来る係数を見つけられたら簡単です。
最高次数と定数項を見ます。
パスカルの三角形は教科書にも載っているので、自分で確認しておくと良いですよ。
こちらの記事でも取り上げています。
(パスカルの三角形は数学\(\,\mathrm{Ⅱ}\,\)ですね。笑)
例題として
\(\hspace{10pt} x^3+6x^2+12x+8\)
を因数分解します。
\(\hspace{4pt} x^3\hspace{4pt}\)の項の係数は「\(\hspace{4pt} 1\,=\,1^3\hspace{4pt}\)」で、
定数項は「\(\hspace{4pt}8\,=\,2^3\hspace{4pt}\)」です。
試しに \( (x+2)^3\) を展開してみると、
\(\hspace{10pt} (x+2)^3\\
=x^3+3(x)^2(2)+3(x)(2)^2+2^3\\
=x^3+6x^2+12x+8\)
ですので、逆に
\(\hspace{10pt} x^3+6x^2+12x+8\\
=(x+2)^3\)
と因数分解できることも確認できます。
これは、ある程度慣れるとすぐに気が付くようになりますよ。
公式4.5.は別に必要ないでしょう。
これに気が付かないなら演習が足りないとしか言えません。
問題数ではなく同じ問題でも良いので反復(復習)しておくといいでしょう。
公式がすぐに適応できない因数分解
次に、③最低次数の文字について整理する。
\(\hspace{10pt} a^3-2a^2b+ab^2+a^2c+b^2c-2abc\)
を因数分解しますが、公式は当てはまりそうもありません。
こんな時は、文字の中で次数の1番低いもので整理すると必ず因数分解できます。
この中で1番次数が低いのは、\(\hspace{4pt}c\hspace{4pt}\)です。
\(\hspace{4pt}\color{red}{c}\hspace{4pt}\)について整理してみましょう。
\(\hspace{10pt} \color{red}{c}(a^2+b^2-2ab)+\color{green}{a^3-2a^2b+ab^2}\)
となります。
ここで重要なポイントがあります。
それは、今、\(\hspace{4pt}c\hspace{4pt}\)について整理しました。
ということは、\(\hspace{4pt} \color{red}{a\,,\,b は定数}\hspace{4pt}\)と見なしているということです。
そして、この定数項、
\(\hspace{10pt}\color{green}{a^3-2a^2b+ab^2}\)
が必ず因数分解出来るようになっているということです。
(できない場合は、因数の1つが1ということになります。)
定数項を因数分解しながら、全体の因数分解を続けましょう。
\(\hspace{10pt} a^3-2a^2b+ab^2+a^2c+b^2c-2abc\\
=c(a^2+b^2-2ab)+a^3-2a^2b+ab^2\\
=c(a-b)^2+a(a^2-2ab+b^2)\\
=c(a-b)^2+a(a-b)^2\\
=(a-b)^2(c+a)\)
1行目 → 2行目: \(\hspace{4pt}c\hspace{4pt}\)について整理した。
2行目 → 3行目: 定数項を部分的に因数分解した。
3行目 → 4行目: 共通因数を見つけた。
4行目 → 5行目: 共通因数をくくりだした。
というふうに定数項に必ず共通因数が出てくるように問題が作られていると考えて因数分解を進めて下さい。
最低次数の文字がなければ、(最低次数の文字が複数あるなら)、
最低次数の1つの文字について整理すると同じように、定数項が因数分解できて、
共通因数が出てきますから、いくつか練習してみて下さい。
「オイラーの分数式」なんかいい練習になると思いますよ。
1週間だけでも毎日1回やっておけば、
後は因数分解の練習は必要無くなる、と良いですね。
ちょっと特殊な因数分解
④の因数分解は、今までの方法ではできないものです。
その中でも因数定理を使う物は省いて、1つだけ、紹介しておきます。
例「\(\hspace{10pt} x^4+x^2+1\hspace{4pt}\)を因数分解せよ。」
という問題です。
これは、\(\hspace{4pt}x^2\hspace{4pt}\)をAなどとおいても決着しません。
全ての項が\(\hspace{4pt} x\hspace{4pt}\)の偶数乗であることに気が付けば、次のようなことができます。
\(\hspace{10pt} (x^2+1)^2=x^4+2x^2+1\)
なので、
\(\hspace{10pt} x^4+x^2+1\\
=x^4+2x^2+1-x^2\\
=(x^2+1)^2-x^2\\
=(x^2+1+x)(x^2+1-x)\\
=(x^2+x+1)(x^2-x+1)\)
3行目から4行目に移る際に
\(\hspace{10pt} a^2-b^2=(a+b)(a-b)\)
を利用しています。
以上でほとんどカバー出来るはずです。
まとめ的になりましたが練習問題をいくらかこなして覚えていって下さい。
大学入試までこの方法で大丈夫です。
「因数分解せよ」と問題にあれば、必ず因数分解できるはずだから、
上の①~④を手順として思い出せるようになって下さい。
ここにあげた因数分解公式は、何度か練習して覚えておくしかないものばかりですよ。
5.の証明をしておきます。
証明)
\(\hspace{10pt} a^3+b^3+c^3-3abc\\
=(a+b)^3-3ab(a+b)+c^3-3abc\\
=(a+b)^3+c^3-3ab(a+b)-3abc\\
=(a+b+c)\{(a+b)^2-c(a+b)+c^2\}-3ab(a+b+c)\\
=(a+b+c)(a^2+2ab+b^2-ca-bc+c^2-3ab)\\
=(a+b+c)(a^2+b^2+c^2-ab-bc-ca)\)
基本対称式を利用した証明となります。
ちょっと特殊でしょう?
公式として覚えた方が早いですね。
証明は、「\(\hspace{4pt} a^3-b^3=(a+b)^3-3ab(a+b)\hspace{4pt}\) を利用する。」
と覚えておかないと、一筋縄ではいかない証明です。
公式は、展開を逆にすれば成り立っていることはすぐにわかります。
\(\hspace{10pt} (a+b+c)(a^2+b^2+c^2-ab-bc-ca)\\
=a^3+b^3+c^3-3abc\)
公式ばかり見ていても役に立ちません。
タスキガケの練習はしておきましょう。
数学\(\,Ⅱ\,\)の範囲になりますが因数分解だけは誰にも負けたくない、と思うならやり遂げて下さい。
2重根号の外し方は少し応用になりますが、基本的な因数分解公式を使うだけです。
数学\(\,Ⅰ\,\)が数学の基本だとすると「数と式」は基本中の基本ですね。