2次関数における係数決定は文字を含んだ問題になるのでよく出ます。
最大最小を文字式で扱う問題の前に、先ずは基本的な係数決定ができる必要がありますので確認しておきましょう。。
また、平衡移動した式の求め方は2次関数に限ったことではありませんが重要なところです。
3点を通る2次関数の決定方法
2次関数は異なる3点があれば決まります。
\( y=ax^2+bx+c\)
という関数なので係数が3つあることからもわかるでしょう。
教科書にはもっと基本的な問題があると思いますが、
計算が1番面倒な「3点を通る条件を満たす2次関数」の求め方をやっておきます。
これができれば係数決定問題はすべて解けるんですよ。
3点 \( (-1,0) , (0,-1) , (2,3)\) を通るグラフをもつ2次関数を求めよ。
2次関数は、
一般形 \( y=ax^2+bx+c\)
標準形 \( y=a(x-p)^2+q\)
と表されるので、3点があれば必ず係数が決定出来ます。
(未定係数が3つだから)
頂点が分かっているときは、\((p,q)\) が分かるので他の1点があれば決定出来ます。
軸 \( \color{red}{x=p}\) が分かっているときは、未定係数が2つとなるので2点があれば求まります。
このように、与えられた条件によって早い求め方が違いますが、係数を決定するということにかわりはありません。
一般形を使うか、標準形を使うかはそのときに応じて使い分ければ良いのです。
基本的に「軸」や「頂点」が与えられたときは標準形を使うと楽な場合が多いです。
例題1のように3点が与えられたときは、三元(文字3つ)の連立方程式を解かなければならないので、計算が一番面倒かもしれません。
展開が不要な分、標準形よりは一般形を使った方が良いですよ。
一般形 \( y=ax^2+bx+c\) に与えられた3点を代入すると、
\( \begin{cases}
\hspace{10pt} 0=a-b+c\\
-1=c\\
\hspace{10pt} 3=4a+2b+c \end{cases}\)
の連立方程式が成り立つのでこれを解いて、
\( a=1,b=0,c=-1\)
これから求める2次関数は、\(y=x^2-1\)。
とするのが一般的な解答なので覚えておきましょう。
ちょっと違った場合も紹介しておきます。
同じように異なる3点が与えあられた場合でも、
「2点の \(y\) 座標が同じ値である場合」です。
例えば、
\( (-3,0) , (1,0) , (-2,-6)\) の3点を通る
という場合、\((-3,\color{red}{0}) , (1,\color{red}{0})\) の2点は \(y\) 座標が同じなので、
(この場合は \( x\) 軸との交点ですが)
この2つの \(x\) 座標の中点を軸が通ります。
何故かというと、2次関数は軸に対して対称なので、
\(y\) 座標が同じ値であればその真ん中に軸があると言えるのです。
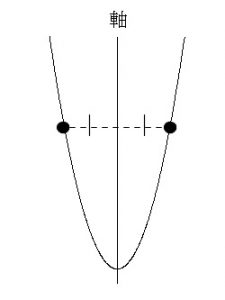
だから、この場合は、標準形で \(y=a(x+1)^2+q\) と置いて、どれか2点を代入しても求まります。
(中点の \( x\) 座標は-1 )
この問題は \( y\) 座標が0の2点が与えられている、
つまり \( x\) 軸との2交点が与えあられていることになるので、
\( y=a(x+3)(x-1)\) と置くと早いです。
これは、「 \( x\) 軸は \( y=0\) という直線」なので、
2次関数を方程式としてみたときの解が、
\( x=-3,1\) であると言うことです。
よって、
\( 0=a(x+3)(x-1)\) を満たしているということです。
後は \( y=a(x+3)(x-1)\) にもう1点を代入すれば求まります。
他に、ちょっと見極めにくいですがでは、
\( (-3,0) , (1,0) , (-2,-6)\) の3点なので、
\((-1,0)\) を通ることから \( (\color{red}{x+1})\) という因数と、
\((0,\color{red}{-1})\) を通ることから
\( y=(\color{red}{x+1})(ax\color{red}{-1})\)
と置くことも可能なのですが、もう少し基本的な問題になれてからやりましょう。
軸がわかっているときの2次関数の決定
軸が \( x=-1\) で、2点 \( (2,3) , (-2,5)\) を通る2次関数を求めよ。
軸が \( x=-1\) と分かっているので、標準形を使いましょう。
求める2次関数を \( y=a(x+1)^2+q\) とおくと、
\( (2,3) , (-2,5)\) を通ることから、
\( \begin{cases}
3=a(2+1)^2+q\\ \\
5=a(-2+1)^2+q \end{cases}\)
⇔
\( \begin{cases}
9a+q=3\\ \\
\hspace{8pt} a+q=5 \end{cases}\)
より、
\(\displaystyle a=-\frac{1}{4} , q=\frac{21}{4}\)
よって求める2次関数は、
\( y=-\displaystyle \frac{1}{4} \left( x+1 \right)^2+\displaystyle \frac{21}{4}\)
(展開しても可)
2次関数は異なる3点があれば決定出来ます。
だから2次関数のグラフを書く場合、異なる3点を座標上に記入します。
頂点が分かっている場合は、頂点と他の1点の座標で構いません。
グラフを書く場合、2次関数が決定出来るだけの点を記入するということです。
平衡移動する2次関数の求め方
グラフが \( y=-3x^2\) のグラフを平行移動したもので、
点 \( (5,-46)\) を通り、頂点が直線 \( y=3x-1\) の上にある2次関数を求めよ。
「 \( y=-3x^2\) のグラフを平行移動したもの」
だから、求める2次関数の \( x^2\) の係数は変わらないので、
\( y=-3x^2+bx+c\) もしくは \( y=-3(x-p)^2+q\)
と置けますが、あと2定点が与えられていません。
(「頂点が \( y=3x-1\) 上にある」とは条件にありますが、定点ではない。)
そこで、頂点の座標を文字で置きます。
これは「おきまり」といっても良いくらいの手法なので忘れないで下さい。
頂点が \( y=3x-1\) あることより、頂点の座標を \( (t,3t-1)\) とおくと、
求める2次関数は、
\( y-(3t-1)=-3(x-t)^2\)
つまり
\( y=-3(x-t)^2+(3t-1)\) ・・・①
とおける。
ここです。
\(\color{red}{ x 座標を t とおくと y 座標も t で}\) 表すことができます。
ここが出来れば決まっていない文字が1つになるので、もう1点あれば決まります。
\( y=-ax^2\) が \( \color{red}{ (p,q)}\) を通るとき
\( y-\color{red}{q}=a(x-\color{red}{p})^2 \hspace{7pt}\Leftrightarrow \hspace{7pt}y=a(x-\color{red}{p})^2+\color{red}{q}\)
と合わせて重要なポイントなので何度も復習して置いてください。
問題に戻ります。
① が \( (5,-46)\) を通ることより、
\( -46=-3(5-t)^2+(3t-1)\)
この \( t\) についての2次方程式を解くと、
\( t=1,10\) であるから、求める2次関数は、
\( y=-3(x-1)^2+2\) および \( y=-3(x-10)^2+29\)
展開する必要はないと思いますが、一応一般形にしておくと、
\( y=-3x^2+6x-1\) および \( y=-3x^2+60x-271\)
「頂点が \( y=3x-1\) 上にある」
「点 \( (5,-46)\) を通る直線は1つではない」
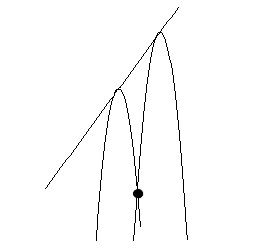
ということはグラフを書いてある程度予測できることなので、
大まかなグラフは書いて考えると良いですね。
「頂点を文字で置く」、忘れないでください!
グラフが書けるというのはそれ以前の問題です。
