関数のグラフは2次関数だけではありません。
2次関数の中でも部分的に絶対値の付いたグラフや最大値、最小値の問題もあります。
絶対値を含むいろいろな関数のグラフが書けるようになることと、それを利用した最大最小の求め方、解き方を確認しておきましょう。
最大値、最小値を求める最大の方法
最大値、最小値はグラフをできる限り細かく情報を入れて書けば分かります。
ただ、グラフを書かなくても求まる方法があるというだけで、
「グラフより」
という言葉を使って解答すればすべて解ける、といっても良いでしょう。
グラフが書きづらい場合もあるので、グラフだけ、ともいきませんが最も単純に答えの出せる方法はグラフを書くことです。
絶対値やルートの中が平方数の場合の根号の外し方
絶対値がついた値は正の数、または\(\,0\,\)になります。
なので絶対値の中が、
正の数のときはそのまま、
負の数ときはマイナスをつけて、
絶対値を外します。
一般的に書くと
\(\begin{equation}
|\mathrm{A}|= \left \{
\begin{array}{l}
\,\mathrm{A} (\,\mathrm{A}\,≧\,0\,のとき) \\
-\mathrm{A} (\mathrm{A}\,<\,0\,のとき)
\end{array}
\right.
\end{equation}\)
等号はどちらにつけても同じです。
これはルートの中が平方数のときも同様です。
\(\begin{equation}
\mathrm{\sqrt{A^2}}= \left \{
\begin{array}{l}
\,\mathrm{A} (\,\mathrm{A}\,≧\,0\,のとき) \\
-\mathrm{A} (\mathrm{A}\,<\,0\,のとき)
\end{array}
\right.
\end{equation}\)
ルート(根号)の前の\(\,+\,\)が省略されているけど数値全体としては正の数なので、
ルートを外した後は\(\,+\,\)、または\(\,0\,\)になっていなければなりません。
絶対値が2つあるときのグラフの書き方
関数 \(y=|x-1|+|2x+2|\) のグラフをかけ。
『絶対値』の定義は中学で覚えていると思います。
『原点からの距離』のことを絶対値といいます。
『距離』とは、数学では『最短距離』を意味するという説明はいいですね。
平面、空間問わず「点と直線」、空間における「点と平面」との距離などでも最短距離のことですよ。
この問題では絶対値の外し方が問題になります。
絶対値の記号は、中身が正の場合+としてそのまま外せば良いですが、
中身が負の場合は-を付けて正の値として外します。
(中身が0の場合はどちらでも良いので場合分けしたどちらかに含ませれば良いです。)
例えば、|3|と中身が正の場合は|3|=3とそのまま外せばいい。
|-3|の場合は中身が負なので|-3|=-(-3)=3と-を付けて外すように、整式などの場合も同じようにすれば良いのです。
この関数は絶対値がついている部分が2つありますので、
2つとも中身が0になる \(x\) を探し、すべてを場合分けします。
境界となる数値で場合分けの範囲を決めるのです。
その際、数直線を利用しましょう。
\(|x-1|\) の中身を0にする \(x\) の値は \(x=1\)
\(|2x+2|\) の中身を0にする \(x\) の値は \(x=-1\)
これらから

3つの部分に分けて絶対値を外します。
ⅰ)
\(x<-1\) のとき
\( y=-(x-1)-(2x+2)\\ \\
=-3x-1\)
ⅱ)
\( -1 < x < 1\) のとき
\( y=-(x-1)+(2x+2)\\ \\
=x+3\)
ⅲ)
\( 1< x\) のとき
\( y=+(x-1)+(2x+2)\\ \\
=3x+1\)
それぞれの部分が「正」か「負」の判断は、範囲内にある代表的な分かり易い数値を入れて見ると簡単に判断できます。
((ⅰ)では-2 , ⅱ)では0 , ⅲ)では2などの範囲内の数値を入れて見る。)
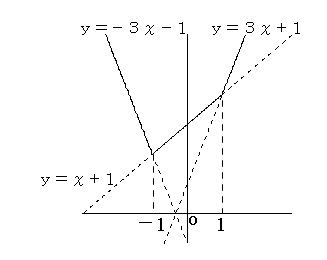
答えは、「図の実線部分」、となります。
場合分けのポイントは、「メンドクサイ」と思ったら終わり!だということです。
2次関数部分に絶対値が付いている問題とグラフの書き方
\(y=|x^2-2|-x\) の \(-2≦ x ≦ 2\) における最大値と最小値を求めよ。
これも絶対値がついた関数なので場合分けが必要です。
\(|x^2-2|\) の中身、\(x^2-2=0\) となるのは \(x=\pm \sqrt{2}\) なので
\(x =-\sqrt{2}\) と \(x =+\sqrt{2}\) が場合分けの境界となります。

3つに場合分けすれば良いだけです。
数値が整数であろうが無理数であろうが関係ありませんよ。
ⅰ)
\(x< -\sqrt{2}\) のとき \(|x^2-2|=\color{red}{+}(x^2-2)\)
このとき
\( y=x^2-2-x\\ \\
=\left(x-\displaystyle \frac{1}{2}\right)^2-\displaystyle \frac{9}{4}\)
ⅱ)
\(-\sqrt{2}≦ x ≦ \sqrt{2}\) のとき \(|x^2-2|=\color{red}{-}(x^2-2)\)
このとき
\( y=-x^2+2-x\\ \\
=-\left(x-\displaystyle \frac{1}{2}\right)^2+\displaystyle \frac{9}{4}\)
ⅲ)
\(\sqrt{2} < x\) のとき \(|x^2-2|=\color{red}{+}(x^2-2)\)
このとき
\( y=x^2-2-x\\ \\
=\left(x-\displaystyle \frac{1}{2}\right)^2-\displaystyle \frac{9}{4}\)
ⅰ)ⅱ)ⅲ)より、\(y=|x^2-2|\) のグラフは、定義域が \(-2≦ x ≦ 2\) なので、
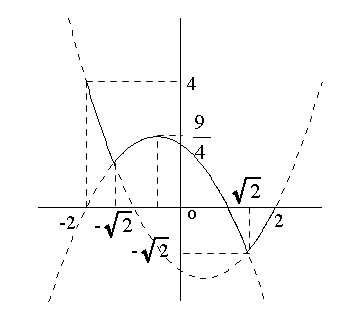
「図の実線部分」となります。
よって、(グラフより)
最大値は \(x=-2\) のとき \(y=4\)
最小値は \(x=\sqrt{2}\) のとき \(y=-\sqrt{2}\)
ⅰ)とⅲ)はまとめても問題ありませんが、場合分けしてみました。
解答上では同じ関数になるので分けなくても良いです。
平方完成も同じ形だから二度する必要はありません。
重要なのは、
「どこが最大で、どこが最小か分かるようにグラフを仕上げる」
ということです。
(わかる場合は『増減表』でも構いませんよ。)
場合分けは式だけをながめているとなかなかできません。
数直線とグラフを多いに利用してください。
基本は同じことです。
ほんの少し手を動かせるようになると、数学の力は大きく変わりますからね。
