2021年(令和3年)度共通テストの数学Ⅱ・数学Ｂの問題と解説

2021年度入試が初の実施となった大学入学共通テスト（共通テスト）数学Ⅱ・数学Ｂの問題と解説です。
必答問題が２問、選択問題２問、太郎さんと花子さんが登場すること以外はセンター試験とそれほど変わりはありません。
ⅡＢ全般の基本をおさえておけば誘導がしっかりあるので取り組みやすいです。

2021年（令和3年）度共通テストの数学Ⅱ・数学Bの問題

２０２１年度共通テスト数学ⅡＢの問題です。

⇒　2021年（令和3年）度共通テスト数学ⅡBの問題

第３問は解説しませんので問題から削除しています。

2021年（令和3年）度共通テストの数学Ⅱ・数学B（必答問題）の解説

第１問第２問は必答問題、第４問第５問は選択問題です。
※
このページは必答問題だけの解説になります。

第１問（必答問題）の解説

〔１〕三角関数です。

(1)「問題\(\,\mathrm{A}\,\)」について考えます。

\(\color{black}{\fbox{　問題Ａ　}}\)

関数
　\(\displaystyle y=\sin\theta+\sqrt{3}\cos\theta\,\left(0≦\theta≦\frac{\pi}{2}\right)\)
の最大値を求めよ。

合成すればすぐに答えは出ますが、
合成の仕方が誘導されています。

三角関数の合成は加法定理を利用して、
\(\,\sin\,\)と\(\,\cos\,\)のどちらでもできます。

⇒　三角関数の合成の公式と合成のやり方

普段どちらを使うかは「好み」ですのでどちらでも良いですが、
(1)では\(\,\sin\,\)を利用して合成します。

\(\hspace{10pt}\,\sqrt{1^2+\sqrt{3}^2}=2\,\)
なので
　\(\begin{eqnarray}\displaystyle
y&=&\sin\,\theta + \sqrt{3}\cos\,\theta\\
&=&2\left(\sin\,\theta\cdot \color{red}{\frac{1}{2}}+\color{blue}{\frac{\sqrt{3}}{2}}\cdot \cos\,\theta\right)
\end{eqnarray}\)

ここで加法定理
　\(\hspace{4pt}\sin(\theta+\alpha)=\sin\theta \color{red}{\cos\alpha} +\color{blue}{\sin \alpha} \cos \theta\)

と照らし合わすと
　\(\hspace{10pt}\displaystyle \color{blue}{\sin \alpha=\frac{\sqrt{3}}{2}}\,,\,\color{red}{\cos \alpha =\frac{1}{2}}\)

これらを満たすのは
　\(\hspace{10pt}\displaystyle 0≦\theta≦\frac{\pi}{2}\)
において
　\(\hspace{10pt}\displaystyle \alpha=\frac{\pi}{\color{black}{\fbox{　3　}}}\)

つまり
　\(\begin{eqnarray}\displaystyle
y&=&\sin\,\theta+\sqrt{3}\,\cos \theta\\
&=&\color{black}{\fbox{　2　}}\,\sin \left(\,\theta +\frac{\pi}{\color{black}{\fbox{　3　}}}\right)
\end{eqnarray}\)
と合成できます。

また
　\(\hspace{10pt}\displaystyle 0≦\theta≦\frac{\pi}{2}\)
のとき
　\(\hspace{10pt}\displaystyle \frac{\pi}{3}≦\theta +\frac{\pi}{3}≦\frac{5}{6}\,\pi\)

だから関数\(\,y\,\)は\(\displaystyle \,\sin\,\left(\theta +\frac{\pi}{3}\right)\)が最大値\(\,1\,\)となる
　\(\begin{eqnarray}\displaystyle
\theta +\frac{\pi}{3}&=&\frac{\pi}{2}\\
\theta&=&\frac{\pi}{\color{black}{\fbox{　6　}}}
\end{eqnarray}\)
のときに最大値\(\color{black}{\fbox{　2　}}\)となります。

合成はそれほど詳しく説明する必要もないでしょうけど、
　\(\hspace{10pt}\displaystyle a\,\sin \theta +b\,\cos \theta\\
\displaystyle =\sqrt{a^2+b^2}\left(\sin \theta \cdot \frac{a}{\sqrt{a^2+b^2}}+\frac{b}{\sqrt{a^2+b^2}}\cdot \cos \theta\right)\)
のように
　\(\hspace{10pt}\sqrt{a^2+b^2}\)
でくくり出すのは「平方の和が\(\,1\,\)」
　\(\displaystyle \frac{a}{\sqrt{a^2+b^2}}+\frac{b}{\sqrt{a^2+b^2}}=1\)
になるようにするためです。

　\(\hspace{10pt}\sin ^2\,\alpha+ \cos^2\,\alpha=1\)
の公式と一致すると思えば少しは納得できますか？

\(\,1\,\)問目から長い説明になってしまっているので後はチャチャっと進めます。

(2)問題Ｂについて「考える」そうです。

\(\color{black}{\fbox{　問題Ｂ　}}\)

関数
　\(\,\displaystyle y=\sin \theta +p\,\cos \theta\,\left(\,0≦\theta≦\frac{\pi}{2}\right)\,\)
の最大値を求めよ。

問題の順に進めた方が楽ですが、
合成するために変形しておくと、
　\(\begin{eqnarray}\displaystyle
y&=&\sin \theta +p\,\cos \theta\\
&=&\sqrt{1+p^2}\left(\sin \theta \cdot \frac{1}{\sqrt{1+p^2}}+\frac{p}{\sqrt{1+p^2}} \cdot \cos \theta\right)
\end{eqnarray}\)

\(\,\sin\,\)で合成するか\(\,\cos\,\)で合成するかは後で「考えます」。

\(\,(ⅰ)\,\)\(\,p=0\,\)のときです。

　\(\hspace{10pt}y=\sin\theta+p\,\cos\theta\)
は\(\,p=0\,\)のとき
　\(\hspace{10pt}y=\sin\theta\)
となるので
　\(\displaystyle \,0≦\theta≦\frac{\pi}{2}\,\)
において
　\(\displaystyle \,\theta=\frac{\pi}{\color{black}{\fbox{　2　}}}\,\)のとき\(\,y\,\)は最大で最大値\(\color{black}{\fbox{　1　}}\)

\(\,(ⅱ)\,\)\(\,p＞0\,\)のときです。

　\(\begin{eqnarray}\displaystyle
y&=&\sin \theta +p\,\cos \theta\\
&=&\sqrt{1+p^2}\left(\sin \theta \cdot \color{red}{\frac{1}{\sqrt{1+p^2}}}+\color{blue}{\frac{p}{\sqrt{1+p^2}}} \cdot \cos \theta\right)
\end{eqnarray}\)
なので、加法定理
　\(\hspace{10pt}\cos(\theta-\alpha)=\cos\theta\,\color{blue}{\cos\alpha}+\sin\theta\,\color{red}{\sin \alpha}\)
と合わせると\(\,\alpha\,\)が\(\displaystyle \,0＜\alpha＜\frac{\pi}{2}\,\)として
　\(\hspace{10pt}\displaystyle \color{red}{\sin \alpha}=\frac{\color{black}{\fbox{　1　}}}{\sqrt{1+p^2}}\\
\hspace{10pt}\displaystyle \color{blue}{\cos \alpha}=\frac{\color{black}{\fbox{　\(\,p\,\)　}}}{\sqrt{1+p^2}}\)
を満たすものとして
　\(\begin{eqnarray}\displaystyle
y&=&\sin \theta +p\,\cos \theta\\
&=&\sqrt{\color{black}{\fbox{　\(\,1+p^2\,\)　}}}\cos(\theta-\alpha)
\end{eqnarray}\)
と合成できます。

このとき\(\,\theta-\alpha=0\,\)つまり
　\(\hspace{10pt}\theta=\color{black}{\fbox{　\(\,\alpha\,\)　}}\)
のとき\(\,\cos\,0=1\,\)で\(\,y\,\)は最大となり、
　最大値は\(\,y=\sqrt{\color{black}{\fbox{　\(\,1+p^2\,\)　}}}\,\)

\(\,(ⅲ)\,\)\(\,p\,＜\,0\,\)のときです。

\(\displaystyle \,0≦\theta≦\frac{\pi}{2}\,\)において
　\(\hspace{10pt}\cos\theta≧0\)
なので
　\(\hspace{10pt}y=\sin\theta+p\cos\theta\)
は\(\,p\,＜\,0\,\)のときは\(\,\cos\theta\,\)が小さいときほど値は大きくなります。

よって\(\,\cos\theta=0\,\)のとき、
つまり、
　\(\displaystyle \,\theta=\color{black}{\fbox{　\(\,\frac{\pi}{2}\,\)　}}\,\)
のとき\(\,y\,\)は最大で、
　最大値は\(\displaystyle \,y=\sin\frac{\pi}{2}=\color{black}{\fbox{　1　}}\,\)

〔２〕２つの関数
　\(\hspace{10pt}\displaystyle f(x)=\frac{2^x+2^{-x}}{2}\)

　\(\hspace{10pt}\displaystyle g(x)=\frac{2^x-2^{-x}}{2}\)
について考えます。

(1)\(\,x=0\,\)のとき
　\(\begin{eqnarray}\displaystyle
f(0)&=&\frac{2^0+2^0}{2}\\
&=&\frac{1+1}{2}=\color{black}{\fbox{　1　}}
\end{eqnarray}\)
　\(\begin{eqnarray}\displaystyle
g(0)&=&\frac{2^0-2^0}{2}\\
&=&\color{black}{\fbox{　0　}}
\end{eqnarray}\)

また、\(\,f(x)\,\)は「相加平均相乗平均の関係から」（親切ですね。）
　\(\begin{eqnarray}\displaystyle
f(x)&=&\frac{2^x+2^{-x}}{2}\\
&≧&2\sqrt{\frac{2^x}{2}\cdot \frac{2^{-x}}{2}}\\
&=&1
\end{eqnarray}\)

最小値は\(\color{black}{\fbox{　1　}}\)です。

または定数を別にして、
　\(\begin{eqnarray}\displaystyle
f(x)&=&\frac{1}{2}(2^x+2^{-x})\\
&≧&\frac{1}{2}\times 2\sqrt{2^x\cdot 2^{-x}}\\
&=&1
\end{eqnarray}\)
としても同じです。

説明する必要はないとは思いますが、
　\(\begin{eqnarray}\mathrm{A}&=&\mathrm{B}\\
&≧&\mathrm{C}\\
&=&\mathrm{D}
\end{eqnarray}\)
というのは
　\(\hspace{10pt}\mathrm{A=B≧C=D}\)
の順に左から見ていくので\(\,\mathrm{A=D}\,\)とは違います。
（限定的に\(\,\mathrm{A=D}\,\)の場合もあります。）

等号成立は
　\(\begin{eqnarray}\displaystyle
2^x&=&2^{-x}\\
x&=&\color{black}{\fbox{　0　}}
\end{eqnarray}\)

相加平均相乗平均の関係を使うときは、
等号成立を忘れずに確認しておきましょう。

続いて\(\,g(x)=-2\,\)となる\(\,x\,\)を求めます。

　\(\begin{eqnarray}\displaystyle
\frac{2^x-2^{-x}}{2}&=&-2\\
2^x-\frac{1}{2^x}&=&-4\\
\end{eqnarray}\)
ここで\(\,2^x=t\,\)とおくと\(\,t＞0\,\)で
　\(\begin{eqnarray}\displaystyle
t-\frac{1}{t}&=&-4\\
t^2-1&=&-4t\\
t^2+4t-1&=&0\\
t&=&-2\pm \sqrt{5}
\end{eqnarray}\)
\(\,t＞0\,\)なので
　\(\hspace{10pt}t=-2+\sqrt{5}\)

\(\,t=2^x\,\)とおいていたので元に戻すと
　\(\hspace{10pt}\color{red}{2}^\color{blue}{x}=\color{magenta}{-2+\sqrt{5}}\)

定義により
　\(\color{blue}{x}=\log_\color{red}{2}(\color{magenta}{\sqrt{5}-2})\)

または
　\(\hspace{10pt}2^x=-2+\sqrt{5}\)
の両辺を底を\(\,2\,\)とする対数を取ると
　\(\begin{eqnarray}\displaystyle
\log_{2}2^x&=&\log_{2}(\sqrt{5}-2)\\
x&=&\log_{2}(\sqrt{\color{black}{\fbox{　5　}}}-\color{black}{\fbox{　2　}})
\end{eqnarray}\)

⇒　指数関数と対数関数の要点

指数対数は関数なのでグラフもあつかえるようにしておきましょう。

(2)
　\(\hspace{10pt}\displaystyle f(x)=\frac{2^x+2^{-x}}{2}\)

　\(\hspace{10pt}\displaystyle g(x)=\frac{2^x-2^{-x}}{2}\)

この2つの関数において\(\,①\,～\,④\,\)になり立つ関係を導きます。

　\(\begin{eqnarray}\displaystyle
f(-x)&=&\frac{2^{-x}+2^{x}}{2}\\
&=&\color{black}{\fbox{　\(\,f(x)\,\)　}}　･･･①
\end{eqnarray}\)

　\(\begin{eqnarray}\displaystyle
g(-x)&=&\frac{2^{-x}-2^{x}}{2}\\
&=&-\frac{2^{x}-2^{-x}}{2}\\
&=&\color{black}{\fbox{　\(\,-g(x)\,\)　}}　･･･②
\end{eqnarray}\)

　\(\hspace{10pt}
\{f(x)\}^2-\{g(x)\}^2\\
=\{\color{red}{f(x)+g(x)}\}\{\color{blue}{f(x)-g(x)}\}\\
\displaystyle =\color{red}{\frac{2\cdot 2^x}{2}}\times \color{blue}{\frac{2\cdot 2^{-x}}{2}}\\
=2^x\times 2^{-x}\\
=\color{black}{\fbox{　1　}}　･･･③\)

この関係は
　　\(\hspace{10pt}
\{f(x)\}^2-\{g(x)\}^2\\
\displaystyle =\frac{1}{4}(2^x+2^{-x})^2-\frac{1}{4}(2^{x}-2^{-x})^2\\
\displaystyle =\frac{1}{4}(2^{2x}+2+2^{-2x})-\frac{1}{4}(2^{2x}-2+2^{-2x})\\
=1　･･･③\)
としても差はありません。
こちらの方が見やすいかもしれませんね。

　\(\begin{eqnarray}\displaystyle
g(2x)&=&\frac{2^{2x}-2^{2x}}{2}\\
&=&\frac{\color{magenta}{(2^x+2^{-x})(2^x-2^{-x})}}{2}
\end{eqnarray}\)
および
　\(\begin{eqnarray}\displaystyle
f(x)g(x)&=&\frac{2^{x}+2^{-x}}{2}\cdot \frac{2^{x}-2^{-x}}{2}\\
&=&\frac{\color{magenta}{(2^x+2^{-x})(2^x-2^{-x})}}{4}
\end{eqnarray}\)
から
　\(\hspace{10pt}g(2x)=\color{black}{\fbox{　2　}}f(x)g(x)　･･･④\)

与えられた関数に代入すれば自然に出てくる関係式でしょう。

(3)またまた登場太郎さんと花子さんです。
二人の会話はヒントですよ。

\(\,\mathrm{(A)～(D)}\,\)に「具体的な値を代入して」、
つねに成り立つか、成り立たないかを調べます。

もう一度書き出しておきます。
　\(\hspace{10pt}\displaystyle f(x)=\frac{2^x+2^{-x}}{2}\)

　\(\hspace{10pt}\displaystyle g(x)=\frac{2^x-2^{-x}}{2}\)

具体的な\(\,\beta\,\)は何でも良いので\(\,\beta=0\,\)とします。

このとき
　\(\hspace{10pt}\displaystyle \color{red}{f(\beta)=f(0)=1}\)
　\(\hspace{10pt}\displaystyle \color{blue}{g(\beta)=g(0)=0}\)
です。

\(\,\mathrm{(A)}\,\)について、
　\(\begin{eqnarray}\displaystyle
f(\alpha-\beta)&=&f(\alpha)\color{blue}{g(\beta)}+g(\alpha)\color{red}{f(\beta)}\\
f(\alpha-0)&=&f(\alpha)\color{blue}{g(0)}+g(\alpha)\color{red}{f(0)}\\
f(\alpha)&=&g(\alpha)
\end{eqnarray}\)

つねに成り立つとは言えません。

\(\,\mathrm{(B)}\,\)について、
　\(\begin{eqnarray}\displaystyle
f(\alpha+\beta)&=&f(\alpha)\color{red}{f(\beta)}+g(\alpha)\color{blue}{g(\beta)}\\
f(\alpha+0)&=&f(\alpha)\color{red}{f(0)}+g(\alpha)\color{blue}{g(0)}\\
f(\alpha)&=&f(\alpha)
\end{eqnarray}\)

つねに成り立ちます。

これ以外は成り立たないことは問題から分かりますが、
確認しておきます。
　
\(\,\mathrm{(C)}\,\)について、
　\(\begin{eqnarray}\displaystyle
g(\alpha-\beta)&=&f(\alpha)\color{red}{f(\beta)}+g(\alpha)\color{blue}{g(\beta)}\\
g(\alpha-0)&=&f(\alpha)\color{red}{f(0)}+g(\alpha)\color{blue}{g(0)}\\
g(\alpha)&=&f(\alpha)
\end{eqnarray}\)

\(\,\mathrm{(D)}\,\)について、
　\(\begin{eqnarray}\displaystyle
g(\alpha+\beta)&=&f(\alpha)\color{blue}{g(\beta)}-g(\alpha)\color{red}{f(\beta)}\\
g(\alpha+0)&=&f(\alpha)\color{blue}{g(0)}-g(\alpha)\color{red}{f(0)}\\
g(\alpha)&=&-g(\alpha)
\end{eqnarray}\)

ちなみに、
　\(\begin{eqnarray}\displaystyle
g(\alpha+\beta)&=&f(\alpha)\color{blue}{g(\beta)}\color{black}{\fbox{+}}g(\alpha)\color{red}{f(\beta)}\\
g(\alpha+0)&=&f(\alpha)\color{blue}{g(0)}+g(\alpha)\color{red}{f(0)}\\
g(\alpha)&=&g(\alpha)
\end{eqnarray}\)
であれば成り立ちます。

簡単にまとめておくと、
問題にある2つの関数\(\,f(x)\,,\,g(x)\,\)において
　\(\hspace{10pt}f(x+y)=f(x)f(y)+g(x)g(y)\)
　\(\hspace{10pt}g(x+y)=f(x)g(y)+g(x)f(y)\)
は成り立ちます。

　\(\begin{eqnarray}\displaystyle
f(x+y)&=&\frac{1}{2}(\,2^x\cdot 2^y+2^{-x}\cdot 2^{-y}\,)\\
&=&\frac{1}{2}\left(\,2^x\cdot 2^y+\frac{1}{2^x\cdot 2^y}\right)
\end{eqnarray}\)
　\(\begin{eqnarray}\displaystyle
g(x+y)&=&\frac{1}{2}(\,2^x\cdot 2^y-2^{-x}\cdot 2^{-y}\,)\\
&=&\frac{1}{2}\left(\,2^x\cdot 2^y-\frac{1}{2^x\cdot 2^y}\right)
\end{eqnarray}\)
であり、
　\(\hspace{4pt}\displaystyle f(x)\cdot f(y)=\frac{1}{4}\left(2^x\cdot 2^y+\frac{2^x}{2^y}+\frac{2^y}{2^x}+\frac{1}{2^x\cdot 2^y}\right)\)
　\(\hspace{4pt}\displaystyle g(x)\cdot g(y)=\frac{1}{4}\left(2^x\cdot 2^y-\frac{2^x}{2^y}-\frac{2^y}{2^x}+\frac{1}{2^x\cdot 2^y}\right)\)
　\(\hspace{4pt}\displaystyle f(x)\cdot g(y)=\frac{1}{4}\left(2^x\cdot 2^y-\frac{2^x}{2^y}+\frac{2^y}{2^x}-\frac{1}{2^x\cdot 2^y}\right)\)
　\(\hspace{4pt}\displaystyle g(x)\cdot f(y)=\frac{1}{4}\left(2^x\cdot 2^y+\frac{2^x}{2^y}-\frac{2^y}{2^x}-\frac{1}{2^x\cdot 2^y}\right)\)
であることから簡単に導けます。

ただし、試験中にこのようなことをしているヒマはありません。
ヒントの通りに「考える」のが早いですよ。

第２問（必答問題）の解説

第２問は関数とグラフの問題です。

接線や面積を求める問題があるので微分積分の問題でもありますが、
太郎さんや花子さんは登場しませんので簡単に済ませます。
（進めやすい？）

(1)２つの２次関数について考えます。

　\(\hspace{10pt}y=3x^2+2x+3　･･･①\)

　\(\hspace{10pt}y=2x^2+2x+3　･･･②\)

\(\,①\,,\,②\,\)には共通点があります。

「・\(\,y\,\)軸との交点の\(\,y\,\)座標」は、
　\(\,x=0\,\)のときの\(\,y\,\)の値
なので、
　\(\hspace{10pt}y=\color{black}{\fbox{　3　}}\)

「・\(\,y\,\)軸との交点における接線の方程式」は、
　\(\,(\,0\,,\,3\,)\,\)における接線
なので、\(\,①②\,\)のどちらでも良いですが、
\(\,①\,\)から
　\(\hspace{10pt}y’=6x+2\)
から接線の傾きは
　\(\hspace{10pt}y’=6\times 0+2\,=\,2\)
これが\(\,(\,0\,,\,3\,)\,\)を通るので
　\(\begin{eqnarray}
y-3&=&2(x-0)\\
y&=&\color{black}{\fbox{　2　}}x+\color{black}{\fbox{　3　}}
\end{eqnarray}\)

もちろん\(\,②\,\)から
　\(\hspace{10pt}y’=4x+2\)
としても同じ傾きになります。

また、\(\color{black}{\fbox{　エ　}}\)の解答群\(\,⓪\,～\,⑤\,\)のうち、
「\(\,y\,\)軸との交点における接線の方程式が
　\(\hspace{10pt}y=2x+3\)」
になるのは、
　\(\,y\,\)軸との交点も同じ
なので定数項が\(\,+3\,\)である\(\,③④⑤\,\)のどれかで、
　\(\,③\,\)から\(\,y’=4x-2\)
　\(\,④\,\)から\(\,y’=-2x\color{red}{+2}\)
　\(\,⑤\,\)から\(\,y’=-2x-2\)
となるので
　\(\,x=0\,\)のとき\(\,y’=2\,\)
となるのは\(\,\color{black}{\fbox{　④　}}\,\)です。

今まで見てきた２次関数と接線の関係がまとてあります。

\(\,a\,,\,b\,,\,c\,\)を\(\,0\,\)出ない実数とすると
　「曲線　\(\,y=ax^2+bx+c\,\)
　上の点\(\,(\,0\,,\,\color{black}{\fbox{　\(\,c\,\)　}}\,)\,\)における接線」
は、
　\(\,y’=2ax+b\,\)
なので\(\,x=0\,\)における接線の傾きは\(\,b\,\)となり、
切片が\(\,c\,\)であることから
　\(\hspace{10pt}\displaystyle \ell\,:\,y=\color{black}{\fbox{　\(\,b\,\)　}}x+\color{black}{\fbox{　\(\,c\,\)　}}\)

接線\(\,\ell\,\)と\(\,x\,\)軸との交点は、
\(\,x\,\)軸は\(\,y=0\,\)という直線なので
　\(\begin{eqnarray}\displaystyle
bx+c&=&0\\
bx&=&-c\\
x&=&\frac{\color{black}{\fbox{　\(\,-\,c\,\)　}}}{\color{black}{\fbox{　\(\,b\,\)　}}}
\end{eqnarray}\)

次は面積ですが、
　「\(\,a\,,\,b\,,\,c\,\)が正の次数であるとき」
なので関数\(\,①\,\)または\(\,②\,\)の場合で上下関係を見れば、
　「２次関数が接線より上」
になっているので積分区間はすぐに分かります。

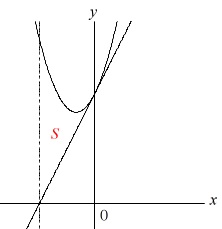
　\(\begin{eqnarray}\displaystyle
S&=&\int_{\frac{-c}{b}}^0 \{(ax^2+bx+c)-(bx+c)\} dx\\
&=&\int_{\frac{-c}{b}}^0 ax^2 dx\\
&=&\left[\frac{1}{3}ax^3\right]_{\frac{-c}{b}}^0\\
&=&0-\left(-\frac{1}{3}a\,\frac{c^3}{b^3}\right)\\
&=&\frac{a\,c^\color{black}{\fbox{　3　}}}{\color{black}{\fbox{　3　}}\,b^\color{black}{\fbox{　3　}}}　･･･③
\end{eqnarray}\)

\(\,③\,\)において\(\,a=1\,\)とすると
　\(\hspace{10pt}\displaystyle S=\frac{c^3}{3b^3}\)

この\(\,S\,\)が一定となるように
　「正の実数\(\,b\,,\,c\,\)の値を変化」
させます。

定数を\(\,k\,\)とでもおいて
　\(\hspace{10pt}\displaystyle k=\frac{c^3}{3b^3}\)
だから
　\(\hspace{10pt}c^3=3k\,b^3\)

この\(\,b\,,\,c\,\)の関係を軸を\(\,b\,\)と\(\,c\,\)で考えても良いのですが、
定数\(\,3k\,\)を\(\,1\,\)としてもグラフの概形は変わらないはずです。
（グラフの軸が\(\,b\,,\,c\,\)であることは見逃さないようにしましょう。）

　\(\begin{eqnarray}\displaystyle
c^3&=&b^3\\
c^3-b^3&=&0\end{eqnarray}\)

左辺を因数分解すると
　\(\,(c-b)(c^2+bc+b^2)=0\,\)

\(\,b\,,\,c\,\)は正の実数なので
　\(\hspace{10pt}c^2+bc+b^2＞0\)
だから
　\(\hspace{10pt}c=b\)

これは原点を通る直線です。

答え　\(\,\underline{　⓪　}\,\)

一般的に考えるなら定数を\(\,3k\,\)の代わりに\(\,t^3\,\)としましょう。
正の定数\(\,3k\,\)となる正の実数\(\,t\,\)は必ず存在します。

もちろん\(\,b\,,\,c\,\)は正の実数なので、
　\(\,t＞0\,\)であり\(\,t^3＞0\,\)
となります。

このとき
　\(\begin{eqnarray}\displaystyle
c^3&=&t^3\,b^3\\
c^3-t^3\,b^3&=&0\end{eqnarray}\)

左辺を因数分解すると
　\(\,(c-tb)(c^2+tcb+b^2)=0\,\)

\(\,b\,,\,c\,,\,t\,\)は正の実数なので
　\(\hspace{10pt}c^2+tcb+b^2＞0\)

よって、\(\,c-tb=0\,\)から
　\(\hspace{10pt}c=tb\)
という原点を通る直線になります。

(2)次は３次関数と接線です。

三つの３次関数\(\,④⑤⑥\,\)のグラフについて考えます。

　\(\hspace{10pt}y=4x^3+2x^2+3x+5　･･･④\)

　\(\hspace{10pt}y=-2x^3+7x^2+3x+5　･･･⑤\)

　\(\hspace{10pt}y=5x^3-x^2+3x+5　･･･⑥\)

「\(\,④⑤⑥\,\)の３次関数のグラフには共通点」があります。
（またか）

「・\(\,y\,\)軸との交点の\(\,y\,\)座標」は
\(\,y\,\)軸は\(\,x=0\,\)なのですべて
　\(\hspace{10pt}y=\color{black}{\fbox{　5　}}\)

次の接線問題の接点が\(\,(\,\color{red}{0}\,,\,\color{blue}{5}\,)\,\)ということです。

「・\(\,y\,\)軸との交点における接線の方程式」は
\(\,④⑤⑥\,\)どれでも良いですが\(\,④\,\)から
　\(\hspace{10pt}y’=12x^2+4x+3\)

\(\,x=0\,\)のとき\(\,y’=3\,\)なので接線は
　\(\begin{eqnarray}\displaystyle
y-\color{blue}{5}&=&3(x-\color{red}{0})\\
y&=&\color{black}{\fbox{　3　}}x+\color{black}{\fbox{　5　}}
\end{eqnarray}\)

またもや一般化します。

\(\,a\,,\,b\,,\,c\,,\,d\,\)を\(\,0\,\)でない実数とすると
　「曲線\(\,y=ax^3+bx^2+cx+d\,\)上の点」
で\(\,x=0\,\)のとき\(\,y=d\,\)なので座標で表すと
　\(\hspace{10pt}(\,0\,,\,\color{black}{\fbox{　\(\,d\,\)　}}\,)\)

　\(\hspace{10pt}y=ax^3+bx^2+cx+d\,\)
から
　\(\hspace{10pt}y’=3ax^2+2bx+c\)
なので\(\,x=0\,\)における接線の傾きは
　\(\hspace{10pt}y’=c\)

接点は\(\,(\,\color{red}{0}\,,\,\color{blue}{d}\,)\,\)なので接線の方程式は
　\(\begin{eqnarray}\displaystyle
y-\color{blue}{d}&=&c(x-\color{red}{0})\\
y&=&\color{black}{\fbox{　\(\,c\,\)　}}x+\color{black}{\fbox{　\(\,d\,\)　}}
\end{eqnarray}\)

次に３次関数とその接線の関係です。

３次関数
　\(\hspace{10pt}\color{red}{f(x)}=ax^2+bx^2+cx+d\)
と\(\,x=0\,\)における接線を
　\(\hspace{10pt}\color{blue}{g(x)}=cx+d\)
とし、
　\(\hspace{10pt}h(x)=\color{red}{f(x)}-\color{blue}{g(x)}\)
を考えます。

　\(\begin{eqnarray}\displaystyle
h(x)&=&f(x)-g(x)\\
&=&(ax^3+bx^2+cx+d)-(cx+d)\\
&=&ax^3+bx^2\\
\end{eqnarray}\)

このとき
　\(\begin{eqnarray}\displaystyle
h'(x)&=&3ax^2+2bx\\
&=&x(3ax+2b)
\end{eqnarray}\)

\(\,h'(x)=0\,\)より
　\(\begin{eqnarray}\displaystyle
x(3ax+2b)&=&0\\
x&=&0\,,\,-\frac{2b}{3a}
\end{eqnarray}\)

\(\,a\,,\,b\,\)は正の実数なので
　\(\hspace{10pt}\displaystyle -\frac{2b}{3a}＜0\)

よって増減表は
　\(\,\begin{array}{c|ccccc}
x & \cdots & -\frac{2b}{3a} & \cdots & 0 & \cdots \\
\hline
h’(x) & + & 0 & – & 0 & + \\
\hline
h(x) & \nearrow & 極大 & \searrow & 0 & \nearrow
\end{array}\,\)

これから\(\,y=h(x)\,\)のグラフの概形は分かります。

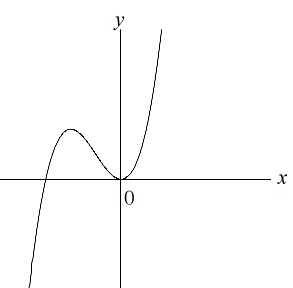
答え　\(\,\underline{　②　}\,\)

\(\,f(x)\,\)のグラフと\(\,g(x)\,\)のグラフの共有点は、
　\(\hspace{10pt}y=f(x)\)
と
　\(\hspace{10pt}y=g(x)\)
を連立すれば求めることができます。

連立すると
　\(\hspace{10pt}f(x)-g(x)=0\)
となりますがこれは
　\(\hspace{10pt}\,h(x)=0\,\)
と同じことです。

\(\,y=h(x)\,\)と\(\,x\,\)軸との交点、
つまり\(\,h(x)=0\,\)を考えると、
　\(\begin{eqnarray}\displaystyle
ax^3+bx^2&=&0\\
x^2(ax+b)&=&0\\
x&=&\color{black}{\fbox{　0　}}\,,\,\frac{\color{black}{\fbox{　\(\,-b\,\)　}}}{\color{black}{\fbox{　\(\,a\,\)　}}}
\end{eqnarray}\)

３次関数と接点\(\,(\,0\,,\,d\,)\,\)における接線を
連立していることになるので接点の\(\,x\,\)座標である
　「\(\,x=0\,\)が重解」
になり、もう一つの解
　\(\hspace{10pt}\displaystyle x=-\frac{b}{a}\)
の\(\,a\,,\,b\,\)ともに正の実数だから
　「負の範囲に\(\,x\,\)軸と交点」
を持つことが分かるので増減表はなくても概形は分かります。

また、\(\,x\,\)が\(\,h(x)=0\,\)の二つの解の間を動くとき、
\(\,h(x)≧0\,\)なので
　\(\,|f(x)-g(x)|=f(x)-g(x)\,\)
となるので\(\,y=h(x)\,\)の極大値がそのまま最大値になります。

増減表から最大（極大）となる\(\,x\,\)の値は
　\(\hspace{10pt}\displaystyle x=\frac{\color{black}{\fbox{　\(\,-2b\,\)　}}}{\color{black}{\fbox{　\(\,3a\,\)　}}}\)

最大値（極大値）は聞かれていません。

後半では積分による面積計算がありませんでしたが、
\(\,f(x)\,\)と\(\,g(x)\,\)で囲まれる部分の面積は、
\(\,y=h(x)\,\)と\(\,x\,\)軸で囲む面積\(\,S\,\)と等しくなります。
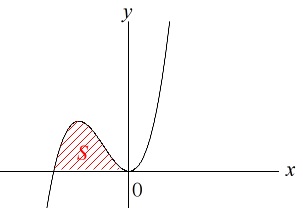このとき、
　\(\begin{eqnarray}\displaystyle
S&=&\int_{\frac{-b}{a}}^{0} h(x) dx\\
&=&\int_{\frac{-b}{a}}^{0} x^2(ax+b) dx\\
&=&\frac{a}{12}\left(0-\frac{-b}{a}\right)^4\\
&=&\frac{b^4}{12\,a^3}
\end{eqnarray}\)
となります。