極大値や極小値などの極値は関数によっては必ず存在するわけではありません。
極値を持つ条件と極値を持たない条件が良く聞かれるので説明しておきます。
極値とはどういうものか、そこから簡単な言葉で説明します。
数学らしい難しい言葉は後からで良いですよ。先ずは感覚的にとらえましょう。
極値を持つか見分けるグラフの概形
中学の数学から思い出して欲しいのですが、直線、つまり１次関数はコブがありません。
コブというのは数学らしい表現とはいえませんが、２次関数はコブが１つあります。
２次関数でいう「上に凸」とか「下に凸」などの凸のところです。
３次関数にはコブが２つあります。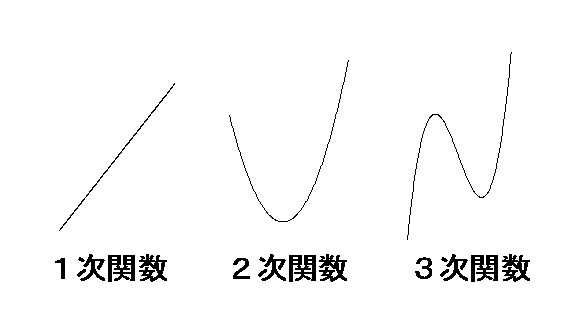
わかりますか？コブ。
４次関数はコブが３つ、５次関数はコブが４つと増えていきます。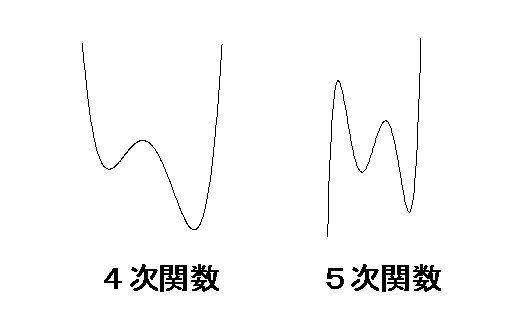
３次関数は一般的にはコブが２つあります。
しかし、コブがない単調増加するものも中にはあるのです。
このコブがない３次関数には極値は存在しません。
グラフでコブがないとき極値は存在しない、では余りにも雑なので数学の条件で表していきます。
極値（極大値や極小値）とは？
そもそも極値とは、定義で説明すると難しいので簡単にいうと、
コブがあるかどうかなのですが、もう少し数学的にいうと
「増えて減っている」または「減って増えている」
点の値のことです。
もう少しいいでしょうか？
「増加から減少に変化する」
または
「減少から増加に変化する」
場合に極値があるといいます。
「増加から減少に変化している」ところを「極大」
「減少から増加に変化している」ところを「極小」
といいます。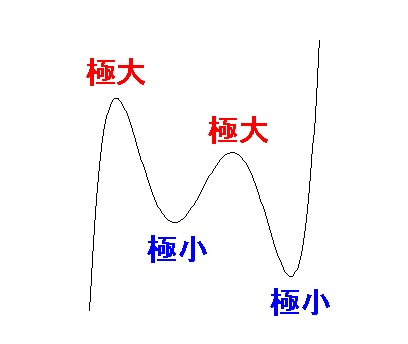
１つの関数に極大、極小が１つとは限りませんよ。
逆に単調に変化する関数のように極値が無い場合もあります。
視覚的に極大、極小が見分けられるようになったところで、
極値が存在する条件を確認しておきましょう。
極値が存在する（極値を持つ）条件
関数 \( y=f(x)\) において極値が存在する条件は、
\( y’=f'(t)=0\) となる \( t\) の前後で、
\(\color{red}{ y’}\) の符号が異なる場合です。
\(\,y’\,\)は微分係数を表しているので接線の傾きのことです。
\(\hspace{10pt} y’\,＞\,0\,\) のときは関数は増加、
\(\hspace{10pt} y’\,＜\,\,0\,\) のときは関数は減少、
を意味しているので
「増減が入れかわっているとき極値をもつ」
ということですね。
簡単に言うと、\( x=t\) の前後で、
増加から減少に移り変われば \(x=t\) で極大値
減少から増加に移り変われば \( x=t\) で極小値
をもつということです。
注意したいのは、
「 \( f'(t)=0\) であっても \( x=t\) で極値をもつとは限らない。」
ことです。
例えば、\( y=x^3\) のとき
\( y’=f'(x)=3x^2\) となり \( f'(0)=0\)
ですが、\(\,y=x^3\,\) は単調増加するので、極値はありません。
しかし、
「 \(f'(t)=0 \) ならば \( y=f(x)\) が極値をもつ」
とはいえませんが、
「 \( y=f(x)\) が \( x=t\) で微分できて、極値をもつなら \( f'(t)=0\) 」
はいえます。
数学\(\,Ⅱ\,\)においては３次関数までで十分で、
３次関数に限っていえば、
\(\hspace{10pt} y=ax^3+bx^2+cx+d\)
が極値を持つ条件は、
\( y’=3ax^2+2bx+c=0\)
が「異なる実数解を持つ」ことで、
判別式 \( D\,＞\,0\)
です。
\( D\,≧\, 0\) ではないことに注意して下さい。
\( D\,=\,0\) のときは増減は変わらないので極値はありません。
極値を持つ条件付き問題の解き方
\(\hspace{10pt} f(x)=x^3-3ax^2+3bx-2\)
が \( x=1\) で極値\(\,2\,\)を取るとき \( a\,,\,b\) の値を求めよ。
この問題を「微分の問題」とみる前に、
文字が２つあるので条件を２つ見つければいい、
というのは頭に置いておいてください。
条件は、
・ \(\,x=1\,\)で極値をとる
・ 極値が\(\,2\,\)
という２つです。
極値という値は \( y\) 座標（ \( f(x)\) の値）のことですよ。
これが分かれば終わったようなものです。
\(\hspace{10pt} f(x)=x^3-3ax^2+3bx-2\)
\(\hspace{10pt} f'(x)=3x^2-6ax+3b\)
条件を並べると
\(\,x=1\,\)で極値を持つことから\(\, f'(1)=0\)
極大値が\(\,2\,\)であることから\(\,f(1)=2\)
連立すると
\(\hspace{10pt} \begin{cases} \hspace{10pt} f'(1)=3-6a+3b=0\\
\hspace{10pt} f(1)=1-3a+3b-2\,=2
\end{cases}\)
これらを解いて
\( \underline{ a=2\,,\,b=3 }\)
ポイントは、
極値を持つなら \( f'(x)=0\) を満たす、
極値は \( f(x)\) で与えられる、
という２つの条件がそろうということです。
極値を持たない条件
極値を持たない条件は、極値を持つ条件の逆です。
「増加減少が入れかわらない。」
それだけです。
２次関数は必ず上に凸か下に凸となるので定義域が実数全体なら極値は必ず存在します。
問題は３次関数の場合ですね。
３次関数 \( y=ax^3+bx^2+cx+d\) が極値を持つ条件が、
\(\, y’=3ax^2+2bx+c=0\) が異なる実数解を持つ
ことで、
判別式 \( \color{red}{D\,＞\,0}\)
なので、極値を持たない条件は、
\(\, y’=3ax^2+2bx+c=0\) が異なる実数解を持たないことで、
判別式 \( \color{red}{D\,≦\, 0}\)
となります。
重解は持っても増減は変わらないので極値にはならない、ということです。
「コブ」の言い方でいうと、
３次関数は多くても２つのコブがありますが、
２つコブがあるときは \( y’=0\) の解が２つあり、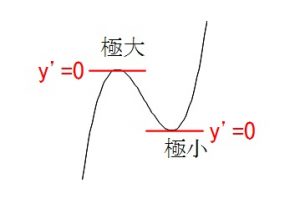
極値は存在します。
コブがないときは \( y’=0\) の解が無いか、重解のときで、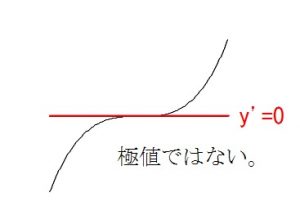
極値はないということですよ。
極値を持たない条件付き問題の解き方
\(\hspace{10pt} f(x)=x^3+x^2+ax+5\)
が極値を持たないような実数 \(a\) の範囲を求めよ。
極値を持たないという条件付きの問題では、
\( a\) の「値」ではなく、
\( a\) の「範囲」を問われることがほとんどです。
関数 \( f(x)=x^3+x^2+ax+5\) が極値を持たないときというのは
関数 \( f(x)\) が単調増加するということです。
つまり、
\(\hspace{10pt} f'(x)=3x^2+2x+a=0\)
の判別式\(\,D\,\)が
\(\hspace{10pt} D/4=1-3a≦ 0\)
を満たせばいいので
\(\hspace{10pt}\displaystyle \underline{ a\,≧\,\frac{1}{3} }\)
４次関数以上は考えなくて良いので、
先ずは３次関数の極値についてグラフの概形とともに考えてみてください。
増減表は微分積分のキモといっても良いです。笑
微分というより増減表を使えば体積の最大値問題も簡単です。
「微分積分」という1つの単元ですが、応用範囲は実に広いです。