対数の方程式、不等式の問題の解き方と方程式が表すグラフや不等式の表す領域を示す方法です。
必ずおさえておく条件や方針としてのポイントがいくつかありますので確認してください。
例題をいくつか上げてみますがどれも同じ方法であると思えるまで繰り返し見ておくと良いです。
対数の方程式と不等式を解くときのポイント
対数の方程式と不等式で必ず確認しておきたいポイントは、
指数の方程式より少しややこしくなるのでここで確認しておきましょう。
対数の方程式と不等式でおさえておきたい共通ポイント
対数の方程式、不等式で共通しておさえておきたいポイントは、
真数と底の条件
です。
定義からの確認事項になりますが、
\(\hspace{4pt}a\,＞\,0\,,a\neq 1\,\)のとき、
\(\hspace{10pt}p=\log_ a N\,\Longleftrightarrow \,a^p=N\)
対数の定義です。
日本語で説明すると
「任意の正の数\(\,N\,\)を1つ定めると、
\(\hspace{4pt}a\,＞\,0\,,a\neq 1\,\)のもとで
\(\,a^p =N\,\)を満たす実数\(\,p\,\)がただ1つ存在する。
このとき\(\,p\,\)を\(\,\log_a N\,\)で表し、
\(\,a\,\)を底とする\(\,N\,\)の対数という。」
となります。
（ややこしいのでここは読み飛ばして良いです。）
また、
\(\,\log_a N\,\)に対し、\(\,N\,\)を\(\,\log_a N\,\)の真数といいます。
ここまでは定義なので説明するまでもないですが、
感覚的ではなく確実に覚えておいてください。
定義ですから説明のしようがありません。
次は対数関数の定義です。
\(\hspace{4pt}a\,\)は\(a\,＞\,0\,,a\neq 1\,\)を満たす定数とする。
このとき
\(\hspace{10pt}y=\log_ a x\, (\,ただし、x\,＞\,0\,)\)
で表される\(\,x\,\)の関数を、
\(\,a\,\)を底とする\(\,x\,\)の対数関数という。
対数の方程式や不等式で必ず確認していおきたい条件が、
この関数における「真数と底の条件」です。
※
指数の方程式では底が正で与えられることが多く場合分けが減ります。
対数の定義同様、
\(\hspace{4pt}y=\log_a x \,\Longleftrightarrow \,x=a^y\)
なので
\(\hspace{2pt}y=a^x\,\)の式で\(\,x\,,\,y\,\)を入れかえたものが\(\,y=\log_a x\)で、
\(\,y=a^x\,\)の逆関数となります。
※逆関数なので\(\,y=x\,\)に関して対称なグラフになります。
ここまでは指数対数の基本で確認しておきましょう。
前置きが長いですが、本番はこれからです。
対数の方程式が表すグラフの表し方
例題を取り上げて対数方程式のグラフの表し方を説明します。
\(\hspace{10pt}\log_x y+2\log_y x=3\)
真数と底の条件を先ず確認します。
\( \begin{cases}
\hspace{4pt} x\,＞\,0\,,\,x \neq 1 ･･･①\\
\hspace{4pt} y\,＞\,0\,,\,y\neq 1 ･･･②
\end{cases}\)
この条件のもとで対数方程式の底を\(\,x\,\)にそろえます。
\(\begin{eqnarray}\displaystyle
\log_x y+2\log_y x&=&3\\
\Longleftrightarrow \log_x y+\frac{2\,\log_x x}{\log_x y}&=&3\\
\Longleftrightarrow \hspace{4pt}\log_x x+\frac{2}{\log_x y}&=&3 ･･･③
\end{eqnarray}\)
底の変換公式は確認しておいてください。
⇒ 対数の計算公式一覧（底の変換と真数の掛け算・割り算の変形のしかた）
いくつもあるとややこしいので、
底はひとつにしておくことを基本にすると良いです。
ここで対数のまとまりを文字にします。
\(\hspace{4pt}\log_x y=t\,\)とすると
\(\hspace{10pt}\displaystyle t+\frac{2}{t}=3\)
こうすると\(\,③\,\)はなじみ深い方程式になるでしょう。
\(\begin{eqnarray}\displaystyle
t^2-3t+2&=&0\\
(t-1)(t-2)&=&0\\
t&=&1\,,\,2 ･･･④
\end{eqnarray}\)
ここでは「\(\,t=1\,\) または \(\,t=2\,\)」です。
\(\,④\,\)を\(\,x\,,\,y\,\)の関係に戻すと
\(\hspace{10pt}\log_x y=1 ･･･⑤\)
または
\(\hspace{10pt}\log_x y=2 ･･･⑥\)
\(\,x\,,\,y\,\)座標で表したいので指数の関係にすると\(\,⑤⑥\,\)は
\(\hspace{10pt}y=x ･･･⑦\)
または
\(\hspace{10pt}y=x^2 ･･･⑧\)
となります。
\(\,①②\,\)かつ\(\,⑦⑧\,\)を図示すると下のグラフになります。
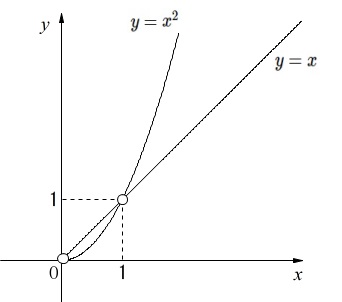
注意点は原点と\(\,○\,\)部分を除外することです。
方程式をグラフで表すのは、
関係式さえ表すことができれば割と簡単です。
対数の不等式の解き方と領域の表し方
対数の不等式では範囲が出てくるので領域になります。
\(\hspace{10pt}\log_x y+2\log_y x\,＞\,3\)
\( \begin{cases}
\hspace{4pt} x\,＞\,0\,,\,x \neq 1 ･･･①\\
\hspace{12pt} y\,＞\,0\,,\,y\neq 1 ･･･②
\end{cases}\)
方程式と同様に不等式の底の変換をします。
\(\begin{eqnarray}\displaystyle
\log_x y+2\log_y x&＞&3\\
\Longleftrightarrow \log_x y+\frac{2\,\log_x x}{\log_x y}&＞&3\\
\Longleftrightarrow \hspace{4pt}\log_x x+\frac{2}{\log_x y}&＞&3 ･･･③
\end{eqnarray}\)
見やすくするために\(\hspace{4pt}\log_x y=t\,\)とすると
\(\hspace{10pt}\displaystyle t+\frac{2}{t}＞3\)
ここで問題になるのが\(\,t\,\)は正か負か定まっていません。
正の数をかけても大小関係は変わりませんが、
負の数をかけると大小関係が逆になります。
そこで\(\,t^2\,＞\,0\,\)を両辺にかけます。
（\(\,t \neq 0\,\)なのでかけても同値関係にあります。）
\(\begin{eqnarray}\displaystyle
t+\frac{2}{t}&＞&3\\
\Longleftrightarrow \hspace{33pt}t^3+2t\,&＞&\,3t^2\\
\Longleftrightarrow \hspace{7pt}t^3-3t^2+2t\,&＞&\,0\\
\Longleftrightarrow \hspace{4pt}t(t^2-3t+2)\,&＞&\,0\\
\Longleftrightarrow \,t(t-1)(t-2)\,&＞&\,0
\end{eqnarray}\)
これを解くと
\(\hspace{10pt}0\,＜\,t\,＜\,1\,,\,2\,＜\,t\)
これから
\(\hspace{10pt}0\,＜\,\log_x y\,＜\,1\hspace{10pt}\)または\(\hspace{10pt}2\,＜\,\log_x y\,\)
ここまでは不等式の処理と変わりません。
ここから場合分けが待っています。
対数関数\(\,y=\log_a x\,\)は底となっている\(\,a\,\)が
\(\hspace{10pt}a\,＞\,1\,\)の場合増加関数
\(\hspace{10pt}0\,＜\,a\,＜\,1\,\)の場合減少関数
になるからです。
本来なら真数および底をそれぞれ場合分けして
\(①\hspace{4pt}\,0\,＜\,x\,＜\,1\,,\,0\,＜\,y\,＜\,1\,\,\)
\(②\hspace{4pt}\,0\,＜\,x\,＜\,1\,,\,1\,＜\,y\,\,\)
\(③\hspace{4pt}\,1＜\,x\,＜\,1\,,\,0\,＜\,y\,＜\,1\,\,\)
\(④\hspace{4pt}\,1＜\,x\,＜\,1\,,\,1\,＜\,y\,\,\)
の４つの場合をそれぞれ調べた方が良いです。
ここでは大小比較であることから
\(\hspace{10pt}0\,＜\,\log_x y\,＜\,1\hspace{10pt}\)または\(\hspace{10pt}2\,＜\,\log_x y\,\)
を全辺を対数にそろえ
\(\hspace{10pt}\log_x 1\,＜\,\log_x y\,＜\,\log_x x\)
または
\(\hspace{10pt}\log_x x^2\,＜\,\log_x y\,\)
と変形することによって底\(\,x\,\)だけの場合分けで済ませます。
\(\,0\,＜\,x\,＜\,1\,\)のとき真数の大小関係は逆になるので
\(\hspace{10pt}1\,＞\,y\,＞\,x\hspace{10pt}または\hspace{10pt}x^2\,＞\,y ･･･③\,\)
\(\,1＜\,x\,\)のとき真数の大小関係はそのままで
\(\hspace{10pt}1\,＜\,y\,＜\,x\hspace{10pt}または\hspace{10pt}x^2\,＜\,y ･･･④\)
\(\,①②\,\)の条件を忘れずに\(\,③④\,\)を図示すると
直線\(\hspace{4pt}y=1\,,\,x=1\,\)を境界として、
下の図のようになります。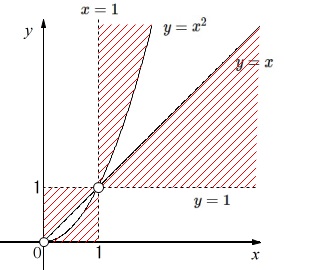
境界と\(○\)の印の点は含みません。
対数方程式をグラフにするのは割と容易ですが、
対数不等式の領域を示すときは、
真数と底の場合分けを忘れないようにしましょう。
対数の真数と底の確認にかなり役に立ちますので
いくつか大学入試の過去問で練習しておくといいですね。
先ずは指数と対数の関数の性質を復習しておきましょう。
指数関数と対数関数は逆関数の関係です。