２０２１年（令和３年）度共通テスト数学２Ｂの選択問題の解説です。
第４問数列と第５問ベクトルの解説になります。
２問とも誘導がしっかりされていますが分量としては十分ありますので、
手を止めたら時間が足りなかった人も多かったかもしれませんね。
第３問の統計は解説しておりません。
２０２１年共通テスト数学ⅡＢの選択問題の問題
２０２１年（令和３年）度数学ⅡＢ選択問題の第４問と第５問の問題です。
第３問は省いてあります。
２０２１年共通テスト数学ⅡＢの選択問題の解説
第４問（選択問題）数列の解説
第４問は数列ですが
等差数列、等比数列
の問題で一般項が分かり易いので、
恒等式の問題として考えれば難しくはありません。
条件を整理しておきます。
数列\(\,\{a_n\}\,\)は初項\(\,3\,\)、公差\(\,p\,\)
数列\(\,\{b_n\}\,\)は初項\(\,3\,\)、公比\(\,r\,\)
\(\,(p≠0\,,\,r≠0)\,\)
さらに\(\,\{a_n\}\,\,,\,\{b_n\}\)は
\(\hspace{6pt}a_nb_{n+1}-2a_{n+1}b_n+3b_{n+1}=0\\
(n=1\,,\,2\,,\,3\,,\,\cdots) ･･･①\)
を満たす。
(1)公差\(\,p\,\)と公比\(\,r\,\)を求めます。
数列\(\,\{a_n\}\,\)は初項\(\,3\,\)、公差\(\,p\,\)の等差数列なので
\(\hspace{10pt}a_n=\color{black}{\fbox{ 3 }}+(n-1)p ･･･②\)
数列\(\,\{a_n\}\,\)の\(\,n\,\)の代わりに\(\,n+1\,\)を入れて
\(\begin{eqnarray}\displaystyle
a_{n+1}&=&3+(n+1-1)\,p\\
&=&3+n\,p ･･･③
\end{eqnarray}\)
また数列\(\,\{b_n\}\,\)は初項\(\,3\,\)、公比\(\,r\,\)の等比数列なので、
\(\hspace{10pt}b_n=\color{black}{\fbox{ 3 }}\cdot r^{n-1}\)
ここで\(\,①\,\)の関係式に\(\,b_{n+1}\,\)があるのに、
何故\(\,b_{n+1}\,\)は表さないのか？
と疑問に思うけど、
必要無いことが次に書いてあります。
※
表しても同じことなので問題ありません。
等比数列は公比をかけると次の項になることから
\(\hspace{10pt}b_{n+1}=r\,b_n\)
を満たしているので
\(\hspace{10pt}\displaystyle \color{red}{\frac{b_{n+1}}{b_n}}=\color{red}{r}\)
となります。
このことから\(\,①\,\)の両辺を\(\,b_n≠0\,\)で割ると
\(\begin{eqnarray}\displaystyle
\frac{a_n\color{red}{b_{n+1}}}{\color{red}{b_n}}-\frac{2a_{n+1}b_n}{b_n}+\frac{3\color{red}{b_{n+1}}}{\color{red}{b_n}}&=&0\\
\color{red}{r}\,a_n-2a_{n+1}+3\color{red}{r}&=&0\\
\end{eqnarray}\)
移項して整理すると
\(\hspace{10pt}\color{black}{\fbox{ 2 }}a_{n+1}=r(a_n+\color{black}{\fbox{ 3 }}) ･･･④\)
\(\,②③\,\)から\(\,a_n\,,\,a_{n+1}\,\)は表されているので\(\,④\,\)に代入すると
\(\begin{eqnarray}\displaystyle
2a_{n+1}&=&=r(a_n+3)\\
2(3+np)&=&r\{3+(n-1)p+3\}\\
6+2np&=&r(6+np-p)\\
&=&6r+rnp-rp\\
2np-rnp&=&6r-rp-6\\
(2-r)np&=&r(6-p)-6
\end{eqnarray}\)
（\(\,n\,\)の恒等式としてみたいので）
両辺に\(\,(-1)\,\)をかけて変形すると
\(\hspace{10pt}(r-\color{black}{\fbox{ 2 }})pn=r(p-\color{black}{\fbox{ 6 }})+\color{black}{\fbox{ 6 }} ･･･⑤\)
\(\,⑤\,\)が\(\,p≠0\,\)ですべての\(\,n\,\)について成り立つことから
\(\hspace{10pt}r-2=0\)
かつ
\(\hspace{10pt}r(p-6)+6=0\)
なので、
\(\,r=\color{black}{\fbox{ 2 }}\,,\,p=\color{black}{\fbox{ 3 }}\,\)
このとき
\(\begin{eqnarray}\displaystyle
a_n&=&3+(n-1)\cdot 3\\
&=&3n
\end{eqnarray}\)
\(\hspace{4pt}b_n=3\cdot 2^{n-1}\)
となっています。
(2)数列\(\,\{a_n\}\,,\,\{b_n\}\,\)の初項から第\(\,n\,\)項までの和を求めます。
\(\begin{eqnarray}\displaystyle
\sum_{k=1}^n a_k&=&\sum_{k=1}^n (3k)\\
&=&3\sum_{k=1}^n k\\
&=&\frac{\color{black}{\fbox{ 3 }}}{\color{black}{\fbox{ 2 }}}n(n+\color{black}{\fbox{ 1 }})
\end{eqnarray}\)
等差数列の和の公式を利用すれば
初項\(\,3\,\)、公差\(\,3\,\)、項数\(\,n\,\)の等差数列
として
\(\begin{eqnarray}\displaystyle
\sum_{k=1}^n a_k&=&\frac{n}{2}\{3+3+(n-1)3\}\\
&=&\frac{3}{2}n(n+1)
\end{eqnarray}\)
となるので同じです。
\(\begin{eqnarray}\displaystyle
\sum_{k=1}^n b_k&=&\sum_{k=1}^n 3\cdot 2^{k-1}\\
&=&\frac{3(2^n-1)}{2-1}\\
&=&\color{black}{\fbox{ 3 }}(2^n-\color{black}{\fbox{ 1 }})
\end{eqnarray}\)
こちらは単なる等比数列の和の公式です。
シグマ計算の公式は使える場合が限られます。
(3)数列\(\,\{c_n\}\,\)の初項は\(\,3\,\)です。
\(\hspace{4pt}a_nc_{n+1}-4a_{n+1}c_n+3c_{n+1}=0 ･･･⑥\)
数列\(\,\{a_n\}\,\)は分かっていますが、
\(\,⑥\,\)を変形してから利用します。
\(\begin{eqnarray}\displaystyle
a_nc_{n+1}+3c_{n+1}&=&4a_{n+1}\,c_n\\
(a_n+3)c_{n+1}&=&4a_{n+1}\,c_n\\
c_{n+1}&=&\frac{\color{black}{\fbox{ 4 }}a_{n+1}}{a_n+\color{black}{\fbox{ 3 }}}\,c_n
\end{eqnarray}\)
さらに\(\,p=3\,\)つまり、
\(\hspace{4pt} \color{red}{a_{n}}\,=\color{red}{3n}\,,\,\color{blue}{a_{n+1}}=\color{blue}{3(n+1)}\)
であることから
\(\begin{eqnarray}\displaystyle
c_{n+1}&=&\frac{4\color{blue}{a_{n+1}}}{\color{red}{a_n}+3}\,c_n\\
&=&\frac{4\cdot \color{blue}{3(n+1)}}{\color{red}{3n}+3}\,c_n\\
&=&\frac{4\cdot 3(n+1)}{3(n+1)}\,c_n\\
&=&4\,c_n
\end{eqnarray}\)
\(\,c_n\,\)を\(\,4\,\)倍すると\(\,c_{n+1}\,\)になるので、
これは数列\(\,\{c_n\}\,\)が
公比\(\,4\,\)（初項\(\,3\,\)）の等比数列
\(\hspace{4pt}c_n=3\cdot 4^{n-1}\)
であることを示しています。
答え \(\,\underline{ ② }\,\)
(4)初項\(\,3\,\)の数列\(\,\{d_n\}\,\)が、
（またか）
\(\hspace{4pt}d_nb_{n+1}-q\,d_{n+1}\,b_n+ ub_{n+1}=0 ･･･⑦\)
\(\hspace{10pt}(n=1\,,\,2\,,\,3\,,\,\cdots )\)
を満たしています。
「\(\,r=2\,\)であることから」、
つまり、
\(\hspace{10pt}b_n=3\cdot 2^{n-1}\)
だから\(\,⑦\,\)は
\(\begin{eqnarray}\displaystyle
q\,d_{n+1}\,b_n&=&(d_n+u)\,b_{n+1}\\
q\,d_{n+1}\,3\cdot 2^{n-1}&=&(d_n+u)\,3\cdot 2^n\\
d_{n+1}&=&\frac{(d_n+u)\,3\cdot 2^n}{q\cdot 3\cdot 2^{n-1}}\\
&=&\frac{2}{q}\,(d_n+u)
\end{eqnarray}\)
数列\(\,\{d_n\}\,\)が、
「公比が\(\,0\,\)より大きく\(\,1\,\)より小さい等比数列」
になるための条件は、
定数\(\,k\,\)が\(\,0＜k＜1\,\)を見たし、
\(\hspace{10pt}d_{n+1}=k\,d_n\)
と表されることなので、
\(\hspace{10pt}q\,＞\,\color{black}{\fbox{ 2 }}\,,\,u=\color{black}{\fbox{ 0 }}\)
が必要十分条件になります。
第４問はここまでです。
条件に沿って等式変形しただけなので解説とは言いがたいですが、
これで終わりです。
和をシグマ（\(\,\sum\,\)）を使って表した以外は、
数列の用語は「等差数列」と「等比数列」しか使っていません。
数列ではまだまだ問われる項目がありますよ。
ただし、
要点の先にある漸化式パターンをすべて解けるようになる必要はありません。
第５問（選択問題）ベクトルの解説
第５問は正五角形と正十二面体をベクトルで考えます。
正五角形はともかく、
正十二面体は幾何ではとらえにくい図形です。
珍しく図が与えられていることからも分かるでしょう。
しかし、ベクトルで考えると機械的とまではいいませんが、
ベクトルの便利さが分かるのではないでしょうか。
(1)１辺の長さが１の正五角形です。
正五角形の対角線の長さはすべて同じで\(\,a\,\)となっています。
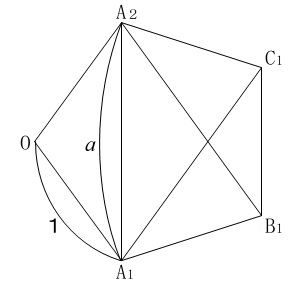さらに正五角形は円に内接するので、
円周角の定理から等しい角と合同な図形がたくさんあります。
いろいろなことが分かりますが、
正五角形の一つの外角が
\(\hspace{10pt}\displaystyle
\frac{360^{\circ}}{5}=72^{\circ}\)
なので\(\,\mathrm{△A_1C_1B_1}\,\)が二等辺三角形であることから、
底角となる
\(\begin{eqnarray}\displaystyle
\mathrm{∠A_1C_1B_1}&=&\frac{72^{\circ}}{2}\\
&=&\color{black}{\fbox{ 36 }}^{\circ}
\end{eqnarray}\)
また円周角は等しくなるので
\(\hspace{10pt}\mathrm{∠C_1A_1A_2}=\mathrm{∠A_1C_1B_1}=36^{\circ}\)
※
当然ですが高校数学は中学の図形は知っているものとしてあります。
復習はしておきましょう。
高校の数学が苦手な人は中学数学が抜けているのかもしれません。
⇒ 中学数学を短期間で攻略する教材
『覚え太郎』を利用して短期間で復習しておきましょう。
もちろん、ベクトルの使い方や要点もまとめてあります。
当会の教材なのでおすすめです。笑
錯角が等しいので\(\,\mathrm{\overrightarrow{A_1A_2}}\,\)と\(\,\mathrm{\overrightarrow{B_1C_1}}\,\)は平行で、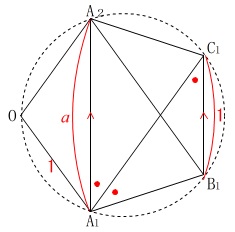
長さの比が\(\,1:a\,\)だから
\(\hspace{10pt} \mathrm{\overrightarrow{A_1A_2}}= \color{black}{\fbox{ \(\,a\,\) }}\,\mathrm{\overrightarrow{B_1C_2}}\)
ここから先何がしたいのかというと、
ベクトルなので「始点を一つ」で見ていきたいのです。
が、説明すると長くなるので問題に従って進めて行きます。
\(\begin{eqnarray}\displaystyle
\mathrm{\overrightarrow{B_1C_1}}&=&\frac{1}{a}\,\mathrm{\overrightarrow{A_1A_2}}\\
&=&\frac{1}{a}\,\left(\mathrm{\overrightarrow{OA_2}}-\mathrm{\overrightarrow{OA_1}}\right) ･･･①
\end{eqnarray}\)
また、
「\(\,\mathrm{\overrightarrow{OA_1}}\,\)と\(\,\mathrm{\overrightarrow{A_2B_1}}\,\)は平行」なので
\(\hspace{10pt}\mathrm{\color{red}{\overrightarrow{A_2B_1}}}=\color{red}{a\,\mathrm{\overrightarrow{OA_1}}}\)
さらに、
「\(\,\mathrm{\overrightarrow{OA_2}}\,\)と\(\,\mathrm{\overrightarrow{A_1C_1}}\,\)も平行」なので
\(\hspace{10pt}\mathrm{\color{blue}{\overrightarrow{A_1C_1}}}=\color{blue}{a\,\mathrm{\overrightarrow{OA_2}}}\)
このとき、
\(\begin{eqnarray}\displaystyle
\mathrm{\overrightarrow{B_1C_1}}&=&\mathrm{\overrightarrow{B_1A_2}}+\mathrm{\overrightarrow{A_2O}}+\mathrm{\overrightarrow{OA_1}}+\mathrm{\overrightarrow{A_1C_1}}\\
&=&-\mathrm{\color{red}{\overrightarrow{A_2B_1}}}-\mathrm{\overrightarrow{OA_2}}+\mathrm{\overrightarrow{OA_1}}+\mathrm{\color{blue}{\overrightarrow{A_1C_1}}}\\
&=&-\color{red}{a\,\mathrm{\overrightarrow{OA_1}}}-\mathrm{\overrightarrow{OA_2}}+\mathrm{\overrightarrow{OA_1}}+\color{blue}{a\,\mathrm{\overrightarrow{OA_2}}}\\
&=&(a-1)\,\mathrm{\overrightarrow{OA_2}}-(a-1)\,\mathrm{\overrightarrow{OA_1}}\\
&=&(\color{black}{\fbox{ \(\,a\,\) }}-\color{black}{\fbox{ 1 }})\left(\mathrm{\overrightarrow{OA_2}}-\mathrm{\overrightarrow{OA_1}}\right) ･･･②
\end{eqnarray}\)
\(\,①②\,\)は同じベクトルを表しているので、
係数が一致するから
\(\begin{eqnarray}\displaystyle
\frac{1}{a}&=&a-1\\
a^2-a-1&=&0\\
a&=&\frac{1\pm \sqrt{5}}{2}
\end{eqnarray}\)
\(\,a＞0\,\)に注意して
\(\hspace{10pt}\displaystyle a=\frac{1+\sqrt{5}}{2}\)
ベクトルを扱うときの基本通りの問題です。
必要ないですが\(\,a\,\)は\(\,\mathrm{\overrightarrow{A_1A_2}}\,\)の大きさなので、
\(\,\cos 108^{\circ}\,\)が求められれば求まります。
※
\(\,18^{\circ}\,,\,36^{\circ}\,,\,72^{\circ}\,,\,108^{\circ}\,\)などの正弦や余弦は、
例えば\(\,36^{\circ}\,\)の場合、
５倍すると\(\,180^{\circ}\,\)になることから、
三角関数の\(\,2\,\)倍角と\(\,3\,\)倍角の公式を利用して求めます。
\(\,a\,\)を求めることが目的ではないので先に進みましょう。
ただし、\(\,a\,\)をわざわざ求めてあるということは、
後で利用するということですよ。
(2)正十二面体です。
正多面体は6つしかありませんが、
そのうちの一つですべての面が正五角形でできています。
ということで空間ベクトルの問題に変わるのですが、
考え方は平面の場合(1)と同じです。
「\(\,\mathrm{\overrightarrow{OA_1}}\,\)と\(\,\mathrm{\overrightarrow{A_2B_1}}\,\)が平行であることから」
\(\hspace{10pt}\mathrm{\color{red}{\overrightarrow{A_2B_1}}}=a\,\mathrm{\overrightarrow{OA_1}}\,\)
なので、
\(\begin{eqnarray}\displaystyle
\mathrm{\overrightarrow{OB_1}}&=&\mathrm{\overrightarrow{OA_2}}+\mathrm{\color{red}{\overrightarrow{A_2B_1}}}\\
&=&\mathrm{\overrightarrow{OA_2}}+\color{black}{\fbox{ \(\,a\,\) }}\,\mathrm{\overrightarrow{OA_1}}
\end{eqnarray}\)
また、
\(\hspace{10pt}|\mathrm{\overrightarrow{OA_2}}-\mathrm{\overrightarrow{OA_1}}|^2=|\mathrm{\overrightarrow{A_1A_2}}|^2\)
において
（左辺）
\(\begin{eqnarray}\displaystyle
|\mathrm{\overrightarrow{OA_2}-\overrightarrow{OA_1}}|^2&=&|\mathrm{\overrightarrow{OA_2}}|^2-2\cdot \mathrm{\overrightarrow{OA_2}}\cdot \mathrm{\overrightarrow{OA_1}}+|\mathrm{\overrightarrow{OA_1}}|^2\\
&=&1^2-2\, \mathrm{\overrightarrow{OA_2}}\cdot \mathrm{\overrightarrow{OA_1}}+1^2\\
&=&2-2\, \mathrm{\overrightarrow{OA_2}}\cdot \mathrm{\overrightarrow{OA_1}}
\end{eqnarray}\)
(1)から\(\displaystyle \,a=\frac{1+\sqrt{5}}{2}\,\)なので
（右辺）
\(\begin{eqnarray}\displaystyle
|\mathrm{\overrightarrow{A_1A_2}}|^2&=&a^2\\
&=&\left(\frac{1+\sqrt{5}}{2}\right)^2\\
&=&\frac{6+2\sqrt{5}}{4}\\
&=&\frac{\color{black}{\fbox{ 3 }}+\sqrt{\color{black}{\fbox{ 5 }}}}{\color{black}{\fbox{ 2 }}}
\end{eqnarray}\)
よって、
\(\begin{eqnarray}\displaystyle
2-2\,\mathrm{\overrightarrow{OA_2}}\cdot \mathrm{\overrightarrow{OA_1}}&=&\frac{3+\sqrt{5}}{2}\\
-2\,\mathrm{\overrightarrow{OA_2}}\cdot \mathrm{\overrightarrow{OA_1}}&=&\frac{3+\sqrt{5}}{2}-2\\
2\,\mathrm{\overrightarrow{OA_2}}\cdot \mathrm{\overrightarrow{OA_1}}&=&-\frac{3+\sqrt{5}}{2}+2\\
&=&\frac{4-3-\sqrt{5}}{2}\\
&=&\frac{1-\sqrt{5}}{2}\\
\mathrm{\overrightarrow{OA_2}}\cdot \mathrm{\overrightarrow{OA_1}}&=&\frac{1-\sqrt{5}}{4}
\end{eqnarray}\)
内積は\(\,\mathrm{\overrightarrow{OA_2}}\cdot \mathrm{\overrightarrow{OA_1}}\,\)も\(\,\mathrm{\overrightarrow{OA_1}}\cdot \mathrm{\overrightarrow{OA_2}}\,\)も同じなので
\(\hspace{10pt}\displaystyle \mathrm{\overrightarrow{OA_1}}\cdot \mathrm{\overrightarrow{OA_2}}=\frac{\color{black}{\fbox{ 1 }}-\sqrt{\color{black}{\fbox{ 5 }}}}{\color{black}{\fbox{ 4 }}}\)
「次に、面\(\,\mathrm{OA_2B_2C_2A_3}\,\)に着目すると」、
（始点\(\,\mathrm{O}\,\)はつながっていることには気をつけておきましょう。）
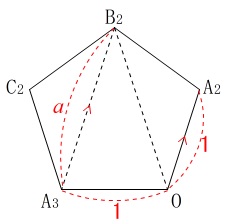正五角形の性質は(1)と同じです。
\(\begin{eqnarray}\displaystyle
\color{red}{\mathrm{\overrightarrow{OB_2}}}&=&\mathrm{\overrightarrow{OA_3}}+\mathrm{\overrightarrow{A_3B_2}}\\
&=&\color{red}{\mathrm{\overrightarrow{OA_3}}+a\,\mathrm{\overrightarrow{OA_2}}} ･･･③
\end{eqnarray}\)
「さらに」長さとなす角が等しいことから
\(\begin{eqnarray}\displaystyle
\mathrm{\overrightarrow{OA_2}}\cdot \mathrm{\overrightarrow{OA_3}}&=&\color{blue}{\mathrm{\overrightarrow{OA_3}}\cdot \mathrm{\overrightarrow{OA_1}}}\\
&=&\color{blue}{\mathrm{\overrightarrow{OA_1}}\cdot \mathrm{\overrightarrow{OA_2}}}\\
&=&\frac{1-\sqrt{5}}{4} ･･･④
\end{eqnarray}\)
「ゆえに」\(\,③④\,\)から
\(\begin{eqnarray}\displaystyle
\mathrm{\overrightarrow{OA_1}}\cdot \color{red}{\mathrm{\overrightarrow{OB_2}}}&=&\mathrm{\overrightarrow{OA_1}}\cdot (\color{red}{\mathrm{\overrightarrow{OA_3}}+a\,\mathrm{\overrightarrow{OA_2}}})\\
&=&\color{blue}{\mathrm{\overrightarrow{OA_1}}\cdot \mathrm{\overrightarrow{OA_3}}}+a\,\mathrm{\overrightarrow{OA_1}}\cdot \mathrm{\overrightarrow{OA_2}}\\
&=&\color{blue}{\mathrm{\overrightarrow{OA_1}}\cdot \mathrm{\overrightarrow{OA_2}}}+a\,\mathrm{\overrightarrow{OA_1}}\cdot \mathrm{\overrightarrow{OA_2}}\\
&=&(1+a)\mathrm{\overrightarrow{OA_1}}\cdot \mathrm{\overrightarrow{OA_2}}\\
&=&\left(1+\frac{1+\sqrt{5}}{2}\right)\frac{1-\sqrt{5}}{4}\\
&=&\frac{3+\sqrt{5}}{2}\cdot \frac{1-\sqrt{5}}{4}\\
&=&\frac{3-3\sqrt{5}+\sqrt{5}-5}{8}\\
&=&\frac{-2-2\sqrt{5}}{8}\\
&=&\color{black}{\fbox{\(\,\frac{-1-\sqrt{5}}{4}\,\)}}
\end{eqnarray}\)
また、\(\,\mathrm{\overrightarrow{OA_1}}\,,\,\mathrm{\overrightarrow{OA_2}}\,,\,\mathrm{\overrightarrow{OA_3}}\,\)を用いて表すと
\(\hspace{10pt}\mathrm{\overrightarrow{OB_1}}=\mathrm{\overrightarrow{OA_2}}+a\,\mathrm{\overrightarrow{OA_1}}\)
\(\hspace{10pt}\mathrm{\overrightarrow{OB_2}}=\mathrm{\overrightarrow{OA_3}}+a\,\mathrm{\overrightarrow{OA_2}}\)
なので、
\(\hspace{10pt}\mathrm{\overrightarrow{OB_1}}\cdot \mathrm{\overrightarrow{OB_2}}\\
=(\mathrm{\overrightarrow{OA_2}}+a\,\mathrm{\overrightarrow{OA_1}})(\mathrm{\overrightarrow{OA_3}}+a\,\mathrm{\overrightarrow{OA_2}})\\
=\mathrm{\overrightarrow{OA_2}}\cdot \mathrm{\overrightarrow{OA_3}}+a\,|\mathrm{\overrightarrow{OA_2}}|^2\\
\hspace{15pt}+a\,\mathrm{\overrightarrow{OA_1}}\cdot \mathrm{\overrightarrow{OA_3}}+a^2\,\mathrm{\overrightarrow{OA_1}}\cdot \mathrm{\overrightarrow{OA_2}} ･･･⑤\\
\)
ここで\(\,④\,\)、\(\,|\mathrm{\overrightarrow{OA_2}}|^2=1\,\)、
および、
\(\begin{eqnarray}a^2-a-1&=&0\\
\color{red}{a^2}&=&\color{red}{a+1}\end{eqnarray}\)
より続きを計算すると、
\(\begin{eqnarray}\displaystyle
⑤&=&(1+a+\color{red}{a^2})\left(\frac{1-\sqrt{5}}{4}\right)+a\\
&=&(1+a+\color{red}{a+1})\left(\frac{1-\sqrt{5}}{4}\right)+a\\
&=&2(1+a)\left(\frac{1-\sqrt{5}}{4}\right)+a\\
&=&2\left(1+\frac{1+\sqrt{5}}{2}\right)\left(\frac{1-\sqrt{5}}{4}\right)+\frac{1+\sqrt{5}}{2}\\
&=&2\left(\frac{3+\sqrt{5}}{2}\right)\left(\frac{1-\sqrt{5}}{4}\right)+\frac{1+\sqrt{5}}{2}\\
&=&\frac{(3+\sqrt{5})(1-\sqrt{5})}{4}+\frac{1+\sqrt{5}}{2}\\
&=&\frac{-2-2\sqrt{5}}{4}+\frac{1+\sqrt{5}}{2}\\
&=&\frac{-1-\sqrt{5}}{2}+\frac{1+\sqrt{5}}{2}\\
&=&\color{black}{\fbox{ 0 }}
\end{eqnarray}\)
ここはうまい計算方法を探すより、
強引に計算を進めた方が早いかもしれません。
空間ベクトルの基本は平面ベクトルと同じで、
扱うベクトルが一つ増えるだけです。
\(\hspace{4pt}a^2-a-1=0\)
については
\(\begin{eqnarray}\displaystyle
\frac{1}{a}&=&a+1\\
1&=&a^2+a\\
a^2-a-1&=&0
\end{eqnarray}\)
と\(\,a\,\)を求めるときに処理しているはずです。
問題が解いてくれているからやってない人もいるかもしれませんね。
その場合は⑤に直接数値を入れて計算しても、
\(\hspace{4pt}\mathrm{\overrightarrow{OB_1}}\cdot \mathrm{\overrightarrow{OB_2}}=0\)
となるので計算してみて下さい。
「最後に」、（もういい）
正五角形の対角線になるので
\(\hspace{4pt}\mathrm{|OB_1|=|OB_2|=|B_2D|=|B_1D|}\)
また、
内積が\(\,0\,\)ということは\(\,\mathrm{OB_1}\,\)⊥\(\,\mathrm{OB_2}\,\)ということです。
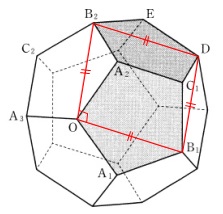
よって平行四辺形のうち、
「ひし形」かつ「長方形」
なので四角形\(\,\mathrm{OB_1DB_2}\,\)は正方形です。
答え \(\,\underline{ ⓪ }\,\)
（問題に書いてある通り）
同一平面にあることは示す必要はありませんが、
\(\,\mathrm{\overrightarrow{OD}}\,\)が\(\,\mathrm{\overrightarrow{OB_1}}\,,\,\mathrm{\overrightarrow{OB_2}}\,\)で表せれば同一平面にあります。
２０２１年度共通テスト数学ⅡＢの問題と解説は以上です。
⇒ 2021年(令和3年)度共通テストの数学Ⅱ・数学Ｂの問題と解説
必答問題からもう一度見通して、
時間配分を考えておきましょう。
数学ⅡＢについてはセンター試験とそれほど違いがあるわけではないです。
（２０２１年度は「考える」とは言えないかもしれませんが）
センター試験の問題はよく考えられているので復習しておくと良いですよ。
ここは対策ページではありませんが、
各単元の基本を忘れないことが一番の対策でしょう。