三角形の五心とは重心・外心・内心・垂心・傍心(ぼうしん)の5つです。
ここではそれぞれの意味(定義)と成り立つ基本定理とその証明をしておきます。
代表的な5心の証明問題も取り上げておきますが、
定理や証明はここで説明するものだけではありませんのでご自身で広げておくと良いでしょう。
三角形の五心とは
三角形には5心(しん)と呼ばれる点があります。
重心・外心・内心・垂心・傍心の5つです。
それぞれの定義を確認し、
成り立つ(利用できる)定理を簡単にですが証明しておきますので、
使えるようになっておきましょう。
(証明はできた方が良いレベルですが「使える」が先で良いです。)
重心
重さに偏りのない板を固定された針の上に置いて、
(または糸でつるして)
バランスを保ち板が水平になる点を重心といいます。
これは後で説明する定理からも直感的に理解できます。
重心の定義
\(\color{red}{\fbox{重心の定義}}\)
三角形の3つの中線の交点を、
その三角形の重心という。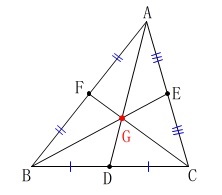 2つの中線の交点が重心\(\,\mathrm{G}\,\)で、
2つの中線の交点が重心\(\,\mathrm{G}\,\)で、
三つ目の中線は必ず\(\,\mathrm{G}\,\)を通ります。
つまり、3中線は必ず重心で交わるということです。
※
中線とは三角形の頂点と対辺の中点を結んだ線、
\(\,\mathrm{AD\,,\,BE\,,\,CF}\,\)の事です。
重心に関する定理
重心について代表的な3つの定理を挙げておきます。
\(\color{blue}{\fbox{ 定理1 }}\)
三角形の3中線は1点で交わる。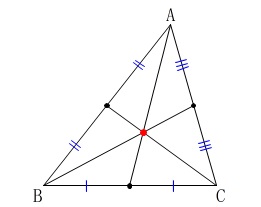
\(\,\mathrm{△ABC}\,\)の3つの中線は1点で交わることを証明せよ。
\(\,\mathrm{△ABC}\,\)において、
\(\,\mathrm{BC\,,\,CA\,,\,AB}\,\)の中点をそれぞれ\(\,\mathrm{D\,,\,E\,,\,F}\,\)とする。
2つの中線\(\,\mathrm{AD\,,\,BE}\,\)の交点を\(\,\mathrm{G}\,\)とし、
\(\,\mathrm{CG}\,\)の延長上に\(\,\mathrm{CG=GK}\,\)となる点\(\,\mathrm{K}\,\)を取る。
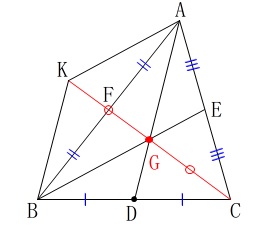 このとき、
このとき、中点連結定理により、
\(\,\mathrm{AG}\,\)∥\(\,\mathrm{KB}\,\)
\(\,\mathrm{AK}\,\)∥\(\,\mathrm{GB}\,\)
となるので四角形\(\,\mathrm{AKBG}\,\)は平行四辺形である。
平行四辺形の対角線はそれぞれの中点で交わるので、
\(\,\mathrm{GK}\,\)は\(\,\mathrm{AB}\,\)の中点\(\,\mathrm{F}\,\)を通る。
つまり、\(\,\mathrm{CF}\,\)は中線であり3中線は1点\(\,\mathrm{G}\,\)で交わる。
※
\(\,\mathrm{K}\,\)の取り方は\(\,\mathrm{AD}\,\)の延長側でも\(\,\mathrm{BE}\,\)の延長側でも良いですよ。
いつも使っていることなので当たり前に思えるでしょうが、
定理はそんなものです。
\(\color{blue}{\fbox{ 定理2 }}\)
重心は中線を\(\,2:1\,\)の比に内分する。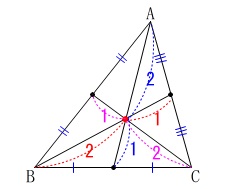
\(\,\mathrm{△ABC}\,\)の重心を\(\,\mathrm{G}\,\)とするとき、
点\(\,\mathrm{G}\,\)は中線を\(\,2:1\,\)の比に内分することを証明せよ。
※
点の取り方は証明例題1と同じで、
言えることも同じなので見直しておいて下さい。
 図のようにそれぞれの点をとる。
図のようにそれぞれの点をとる。ここで
\(\hspace{4pt}\mathrm{CG=GK=2GF}\)
であることから
\(\,\mathrm{CG:GF=2:1}\,\)
同様に\(\,\mathrm{AD\,,\,BE}\,\)も中線なので
\(\hspace{4pt}\mathrm{AG:GD}=2:1\)
\(\hspace{4pt}\mathrm{BG:GE}=2:1\)
\(\color{blue}{\fbox{ 定理3 }}\)
\(\,\mathrm{△ABC}\,\)の重心を\(\,\mathrm{G}\,\)とするとき、
\(\,\mathrm{△GBC=△GCA=△GAB}\,\)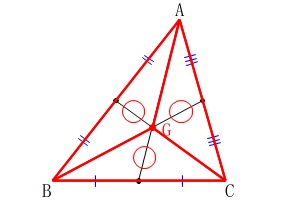
\(\,\mathrm{△ABC}\,\)の重心を\(\,\mathrm{G}\,\)とするとき、
\(\hspace{10pt}\mathrm{△GBC=△GCA=△GAB}\)
であることを証明せよ。
各点を下図の様に取る。
 このとき(定理2から)
このとき(定理2から)\(\hspace{4pt}\mathrm{AG:GD=BG:GE=CG:GF}=2:1\)
\(\,\mathrm{△ABC}\,\)と\(\,\mathrm{△GBC}\,\)に着目すると、
底辺\(\,\mathrm{BC}\,\)を共有するので
\(\hspace{4pt}\mathrm{△ABC:△GBC=AD:GD}=3:1\)
同様に
\(\hspace{4pt}\mathrm{△ABC:△GCA=BE:GE}=3:1\)
\(\hspace{4pt}\mathrm{△ABC:△GAB=CF:GF}=3:1\)
よって
\(\hspace{10pt}\mathrm{△GBC=△GCA=△GAB}\)
他にも言えることはいろいろとあります。
例えば、各点を例題と同じように取るとき、
\(\,\mathrm{△DEF}\,\)の重心は\(\,\mathrm{△ABC}\,\)の重心と同じになります。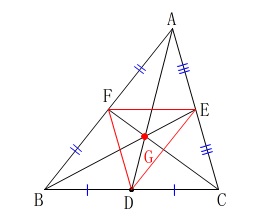 このことはもっと広げることができて、
このことはもっと広げることができて、
\(\,\mathrm{△ABC}\,\)の3辺\(\,\mathrm{BC\,,\,CA\,,\,AB}\,\)を一定の比で内分する点を
それぞれ\(\,\mathrm{P\,,\,Q\,,\,R}\,\)とするとすれば、
\(\,\mathrm{△PQR}\,\)の重心は\(\,\mathrm{△ABC}\,\)の重心と一致します。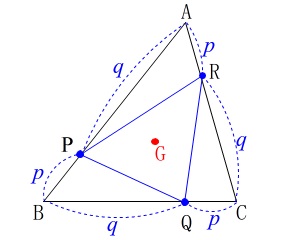 事実だけを知っておいてくれれば良いので証明はしませんが、
事実だけを知っておいてくれれば良いので証明はしませんが、
幾何的な証明は少しややこしいのでベクトルの利用をおすすめします。
外心
\(\,\mathrm{△ABC}\,\)において3頂点\(\,\mathrm{A\,,\,B\,,\,C}\,\)を通る円が1つあります。
この円を\(\,\mathrm{△ABC}\,\)の外接円といいますが、
その中心を外心といいます。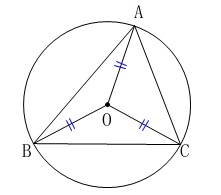 外心を\(\,\mathrm{O}\,\)とすると、
外心を\(\,\mathrm{O}\,\)とすると、
\(\hspace{4pt}\mathrm{OA=OB=OC}\)
なので、いくつか定理があります。
外心の定義
\(\color{red}{\fbox{外心の定義}}\)
三角形の3辺の垂直二等分線は1点で交わり、
その点を外心という。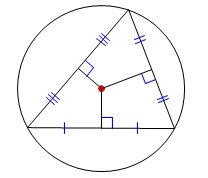 外接円の中心を外心という。
外接円の中心を外心という。
というのを定義にしたいところですが、
三角形にコンパスで外接円を書いてみて下さい。
外接円の中心ってどこ?ってなりますよね。
外心の持つ定理から外接円が言えるので逆なんです。
いくつかの定理とその証明をしておきます。
外心に関する定理
先ずは定義となっている事実の証明です。
\(\color{blue}{\fbox{ 定理1 }}\)
三角形の3辺の垂直二等分線は一点で交わる。
\(\,\mathrm{△ABC}\,\)の3辺\(\,\mathrm{BC\,,\,CA\,,\,AB}\,\)の垂直二等分線は、
1点で\(\,\mathrm{O}\,\)交わることを証明せよ。
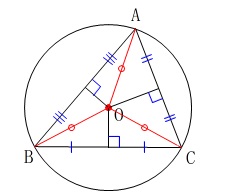 \(\,\mathrm{△ABC}\,\)の2辺\(\,\mathrm{AB\,,\,AC}\,\)の垂直二等分線の交点を\(\,\mathrm{O}\,\)とすると、
\(\,\mathrm{△ABC}\,\)の2辺\(\,\mathrm{AB\,,\,AC}\,\)の垂直二等分線の交点を\(\,\mathrm{O}\,\)とすると、二等辺三角形の性質から
\(\hspace{4pt}\mathrm{OA=OB}\)
\(\hspace{4pt}\mathrm{OA=OC}\)
このことから
\(\hspace{4pt}\mathrm{OB=OC}\)
よって、\(\,\mathrm{O}\,\)は辺\(\,\mathrm{BC}\,\)の垂直二等分線上にある。
これは\(\,\mathrm{△ABC}\,\)の3辺の垂直二等分線が1点で交わることを示している。
\(\color{blue}{\fbox{ 定理2 }}\)
\(\,\mathrm{△ABC}\,\)の3辺の垂直二等分線は一点\(\,\mathrm{O}\,\)で交わり、
\(\hspace{4pt}\mathrm{OA=OB=OC}\)
となる。
これは証明例題1の中で証明は終わっているので例題にしません。
三角形とその外接円の半径との間には正弦定理があります。
すぐに思いつくとは思いますが確認しておきましょう。
一つひとつの事実を知ることは大切ですが、
つなげていけるかどうかが大きな違いになりますよ。
内心
三角形の3辺から等しい距離に等しい点が1つあって、
この点から三角形に内接する円が描けます。
その円の中心を内心といいます。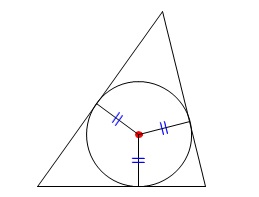 これも外心と同じで、
これも外心と同じで、
内接円の中心を内心というのではなく、
しっかりと定まる定義があります。
内心の定義
\(\color{red}{\fbox{ 内心の定義 }}\)
三角形の各頂角の二等分線の交点を内心という。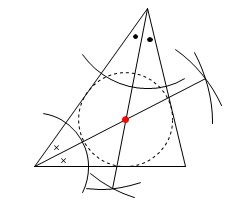 ここでは2つの頂角の二等分線で内心を示していますが、
ここでは2つの頂角の二等分線で内心を示していますが、
続いて定理で証明するように3つ目も内心で必ず交わります。
内心の定理
ここでは定理を2つまとめて紹介しておきます。
※
外心と同様に、証明例題としてまとめて証明できる。
\(\color{blue}{\fbox{ 定理1、定理2 }}\)
三角形の各頂点の二等分線は1点で交わる。
また、この交点は三角形の3辺から等距離にある。
\(\,\mathrm{△ABC}\,\)の3つの内角の二等分線は1点\(\,\mathrm{I}\,\)で交わることを証明せよ。
また、
点\(\,\mathrm{I}\,\)から3辺\(\,\mathrm{BC\,,\,CA\,,\,AB}\,\)への垂線\(\,\mathrm{ID\,,\,IE\,,\,IF}\,\)の長さは等しいことを証明せよ。
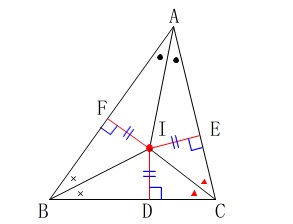 \(\,\mathrm{∠B\,,\,∠C}\,\)の二等分線の交点を\(\,\mathrm{I}\,\)とし、
\(\,\mathrm{∠B\,,\,∠C}\,\)の二等分線の交点を\(\,\mathrm{I}\,\)とし、\(\,\mathrm{I}\,\)から3辺\(\,\mathrm{BC\,,\,CA\,,\,AB}\,\)への垂線を\(\,\mathrm{ID\,,\,IE\,,\,IF}\,\)とする。
\(\,\mathrm{BI}\,\)は\(\,\mathrm{∠B}\,\)の二等分線なので
\(\hspace{4pt}\mathrm{IF=ID}\)
\(\,\mathrm{CI}\,\)は\(\,\mathrm{∠C}\,\)の二等分線なので
\(\hspace{4pt}\mathrm{IE=ID}\)
このことから
\(\hspace{10pt}\mathrm{IF=IE}\)
よって\(\,\mathrm{AI}\,\)は\(\,\mathrm{∠A}\,\)の二等分線でもあるので、
3つの二等分線は1点\(\,\mathrm{I}\,\)で交わる。
また、
\(\hspace{10pt}\mathrm{ID=IE=IF}\)
※
角の二等分線はその角をなす2辺から等しい距離にある点の集まりのことです。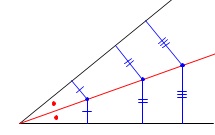 忘れている人は中学の図形から見直しておきましょう。
忘れている人は中学の図形から見直しておきましょう。
『覚え太郎』で復習するのが一番早いです。
垂心
垂心の定義と定理を簡単にまとめておきます。
三角形の形状によっては内心と垂心は近い位置にあるので、
同じ点だと思い込まないように注意が必要です。
垂心の定義
\(\color{red}{\fbox{垂心の定義}}\)
三角形の3頂点から対辺におろした垂線の交点を、
その三角形の垂心という。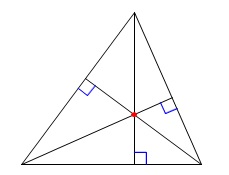 ※
※
外心、内心と同じで2つの垂線の交点が垂心で、
三つ目は必ず垂心で交わります。
垂心の定理
三角形の3頂点から対辺におろした垂線は1点で交わる。
これを証明するとき、
平行四辺形の定理から外心と関係する面白い関係があるので見ておきましょう。
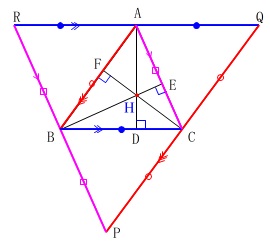
\(\,\mathrm{△ABC}\,\)において3頂点\(\,\mathrm{A\,,\,B\,,\,C}\,\)から対辺に引いた垂線、
\(\,\mathrm{AD\,,\,BE\,,\,CF}\,\)は1点\(\,\mathrm{H}\,\)で交わることを証明せよ。
下図の様に\(\,\mathrm{△ABC}\,\)の3頂点\(\,\mathrm{A\,,\,B\,,\,C}\,\)を通り、
3辺\(\,\mathrm{BC\,,\,CA\,,\,AB}\,\)にそれぞれ平行な直線を引き\(\,\mathrm{△PQR}\,\)をつくる。
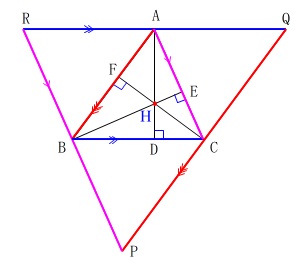 このとき
このとき\(\,\mathrm{AQ}\,\)∥\(\,\mathrm{BC}\,\)、\(\,\mathrm{QC}\,\)∥\(\,\mathrm{AB}\,\)
であるから四角形\(\,\mathrm{ABCQ}\,\)は平行四辺形である。
同様に\(\,\mathrm{RA=BC}\,\)で\(\,\mathrm{RA=AQ}\,\)となるので、
\(\hspace{4pt}\mathrm{BC=AQ}\)
つまり頂点\(\,\mathrm{A}\,\)は\(\,\mathrm{RQ}\,\)の中点である。
 また、
また、\(\,\mathrm{AD⊥BC}\,\)かつ\(\,\mathrm{RQ}\)∥\(\,\mathrm{BC}\,\)
であることから
\(\hspace{4pt}\mathrm{AD}\)⊥\(\,\mathrm{RQ}\,\)
よって、\(\,\mathrm{AD}\,\)は辺\(\,\mathrm{PQ}\,\)の垂直二等分線である。
垂線\(\,\mathrm{BE\,,\,DF}\,\)にも同様のことがいえるので、
\(\,\mathrm{AD\,,\,BE\,,\,CF}\,\)は\(\,\mathrm{△PQR}\,\)の3辺の垂直二等分線であり、
点\(\,\mathrm{H}\,\)は\(\,\mathrm{△PQR}\,\)の外心1点で交わる。
このように三角形の五心はいろいろな関係性を持っています。
あからさまではないですけどよく問題にされるので、
少しだけでも問題集などで確認しておくと良いですね。
幾何としては証明がややこしくなりますが、
基本的な幾何の知識を利用すれば、
ベクトルでは機械的に処理できる事が多いです。
傍心
傍心(ぼうしん)は余り聞き慣れない点ですが、
大学入試センターによって意味が書かれて問題になったことがあります。
傍心の意味は、傍接円の中心の事です。
傍接円とは何か?
その中心となる傍心の定義を見ていきましょう。
三角形には3つの傍心がありますが、
定理を証明してから確認しておきます。
傍心の定義
\(\color{red}{\fbox{傍心の定義}}\)
三角形の1つの頂角と、
他の2角の外角の二等分線の交点を傍心という。 傍心と傍接円自体はイメージしやすいと思いますが、
傍心と傍接円自体はイメージしやすいと思いますが、
内心などと同じように傍心を定めるには定義が必要です。
傍心の定理
外心、内心で見てきたように、
3つの二等分線は必ず1点で交わりますので、
2つの二等分線の交点が傍心になりますが証明しておきます。
\(\,\mathrm{△ABC}\,\)において\(\,\mathrm{∠B\,,\,∠C}\,\)の外角の二等分線と、
\(\,\mathrm{∠A}\,\)の二等分線は1点\(\,\mathrm{J}\,\)で交わることを証明せよ。
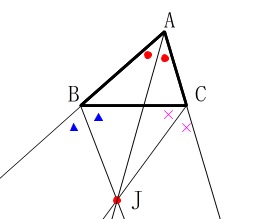 下の図のように、
下の図のように、\(\,\mathrm{∠B\,,\,∠C}\,\)の外角の二等分線の交点を\(\,\mathrm{J}\,\)とし、
\(\,\mathrm{J}\,\)から直線\(\,\mathrm{BC\,,\,CA\,,\,AB}\,\)に垂線\(\,\mathrm{JD\,,\,JE\,,\,JF}\,\)を引く。
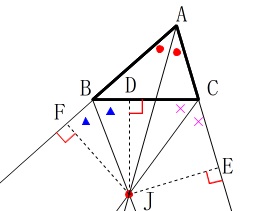 このとき、
このとき、\(\,\mathrm{BJ}\,\)は\(\,\mathrm{∠B}\,\)の外角の二等分線なので
\(\hspace{4pt}\mathrm{JF=JD}\)
\(\,\mathrm{CJ}\,\)は\(\,\mathrm{∠C}\,\)の外角の二等分線なので
\(\hspace{4pt}\mathrm{JE=JD}\)
よって
\(\hspace{10pt}\mathrm{JF=JE}\)
このことから\(\,\mathrm{AJ}\,\)は\(\,\mathrm{∠A}\,\)の二等分線であることが分かる。
つまり、
\(\,\mathrm{∠B\,,\,∠C}\,\)の外角の二等分線と\(\,\mathrm{∠A}\,\)の二等分線は1点\(\,\mathrm{J}\,\)で交わる。
(おわり)
この証明中で分かるように
\(\hspace{10pt}\mathrm{JD=JE=JF}\).
これは1点からの距離が等しいことを意味していて、
点\(\,\mathrm{J}\,\)が傍接円の中心となっていることが分かります。
(3辺に接する円が描ける。)
ここでは\(\,\mathrm{∠A}\,\)の内部にある傍心を\(\,\mathrm{J}\,\)としました。
同じように、
\(\,\mathrm{∠B}\,\)の内部にも傍心\(\,\mathrm{K}\,\)があり、
\(\,\mathrm{∠C}\,\)の内部にも傍心\(\,\mathrm{L}\,\)があります。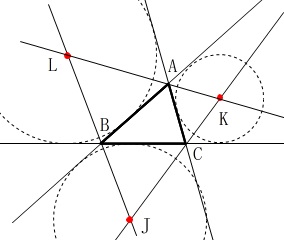 この\(\,\mathrm{△JKL}\,\)の垂心は、
この\(\,\mathrm{△JKL}\,\)の垂心は、
\(\,\mathrm{△ABC}\,\)の垂心だったりします。
ここでは証明しませんが問題集なんかで見つけたら証明をながめておいて下さい。
簡単に説明しておくと、
\(\,\mathrm{BK}\,\)に着目すると、
\(\,\mathrm{∠B}\,\)の二等分線であり\(\,\mathrm{∠B}\,\)の外角の二等分線でもあるので、
\(\hspace{10pt}\mathrm{∠LBK}=90^{\circ}\)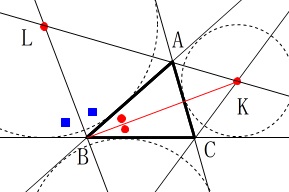 同様のことが\(\,\mathrm{LC\,,\,JA}\,\)にもいえます。
同様のことが\(\,\mathrm{LC\,,\,JA}\,\)にもいえます。
三角形の五心にはいろいろな定理があります。
ここであげている定理は基本定理として覚えておきましょう。
幾何の基本定理とベクトルを組合わせると、
問題解決の視点が広がりますよ。