定義域(x)に範囲がある２次関数のグラフの概形と最大値最小値

２次関数のグラフの概形は、先に学ぶ他の分野でもずっと使いますので書けなくてはなりません。
定義域に範囲（xの範囲）がある場合のグラフを書くときに必要な作業とおさえておくポイントを確認しておきましょう。
最大値、最小値問題は必ず問われることになるので何度も繰り返し説明します。

２次関数を見たらやるべき平方完成とは

２次関数のグラフを書くときに重要なことは、
「平方完成」することです。

それをしないで「２次関数苦手」って、
それは「問題を解く気が無い」と言っても良いくらいです。
すべての問題でグラフが必要なわけではありませんが、少なくとも入試の数学でグラフが必要ない問題は無い、と言っても良いでしょう。
（２変数関数の式処理だけで答えが出る問題などもありますが、例外としておきます。）

先ずは平方完成して下さい。
グラフの概形を書いて下さい。

細かい内容を見るのはそれからです。

あ、ちなみに「平方完成」とは、
　\( y=ax^2+bx+c\)　のような関数の形を、
　\( y=a(x-p)^2+q\)　のような頂点を示せる形にすることです。
※
この用語自体は別にどうでも良いのですが、知っておいてもらえると説明が楽になるので、書いておきます。
もちろん、解答上に書いても不都合なことは全くありませんので使って下さい。

今回は定義域が示されている最大最小問題です。
（定義域は　\( x\)　の範囲のことです。）

例題です。

（１）定義域を見ることやグラフを書くことは後です。
ますは平方完成しましょう。

　\( y=2x^2+x-1\\ \\
=2 \left(x^2+\displaystyle \frac{1}{2}x \right)-1\\ \\
=2 \left(x+\displaystyle \frac{1}{4}\right)^2-2\times \displaystyle \frac{1}{16}-1\\ \\
=2 \left(x+\displaystyle \frac{1}{4} \right)^2-\displaystyle \frac{9}{8}\)

ここまでは必ずやっておくことです。
※
平方完成ができないという人は１日かけても練習しておくべきですよ。

２次関数の最大値、最小値は頂点か定義域の両端

この放物線の頂点は、\(\displaystyle \left(-\frac{1}{4},-\frac{9}{8}\right)\)　となります。

２次関数は異なる３点を決めれば定まるので、
（頂点がわかる場合は２点でも定まります。）
定義域の両端を見ればこの場合はグラフが定まります。

　\( x=-1\)　のとき　\( y=0\)
　\( x=1\)　のとき　\( y=2\)

だからこの放物線は点　\( (-1,0 )　,　(1,2)\)　を通ります。
また、ここでは必要無いですが切片を求めておくと、
　\( x=0\)　のとき　\( y=-1\)　より、\(\color{red}{y\,切片}\)は－１となります。
　（　\( y\, 切片\)は　\( x\)　軸と交わるところです。）

これをグラフにします。

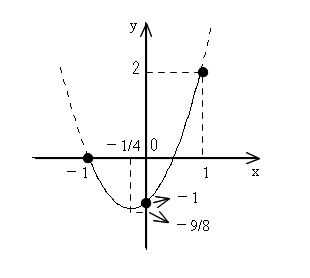
後はグラフから読み取れば良いだけ、となります。

下に凸なグラフで、頂点を定義域に持つので、最小値は頂点の　\(y\)　座標となります。

最大値はグラフから読み取ってもいいですが、軸から遠い　\( x=1\)　のときです。

　\(\displaystyle x=-\frac{1}{4}\)　のとき　最初値　\(\displaystyle -\frac{9}{8}\)
　\( x=1\)　のとき　最大値　\( 2\)

が答えとなります。

定義域に等号が無い場合は最大値、最小値が無い場合がある

（２）　\( y=(x+1)(3-x)\)　（　\( -1 < x< 3\)　）

これは２次関数の特性を知り、慣れてくると平方完成しなくてもグラフはかけるようになりますが、やはり基本通り変形していく方がいいでしょう。
展開して平方完成すると

　\( y=(x+1)(3-x)\\ \\
=-x^2+2x+3\\ \\
=-(x^2-2x)+3\\ \\
=-\{(x-1)^2-1\}+3\\ \\
=-(x-1)^2+4\)

これから頂点は　\( (1,4)\)　で上に凸な放物線だとわかります。
他に１点取ればグラフは定まりますが、ちょっと問題の関数を見てみましょう。

　\( y=(x+1)(3-x)\)

から　\( x=-1\)　と　\( x=3\)　を代入すると、どちらも　\( y=0\)　となるので、
点　\( (-1,0)　,　(3,0)\)　を通ることがわかります。
これは　\(x\)　軸との交点なので、これでグラフは簡単に書けます。

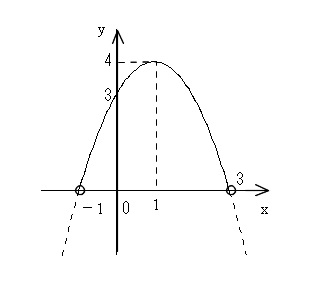
グラフから　\( x=1\)　のとき最大値　４　をとり、
最小値はなし
となります。

この問題では定義域　\( -1 < x < 3\)　の両端に等号が付いていないので、
　\( x=-1\)　と　\( x=3\)　は定義域に含まれていません。

よって　\( y=0\)　とはなりません。（限りなく近づきますが0にはならない）
このようなときは最小値は存在しないということになり「最小値なし」です。
定義域の両端の片方の値があれば最小値は存在する可能性はあります。

ここでは２次関数の最大最小はグラフを見れば良いということをお伝えしました。
例えば次のグラフを見てください。

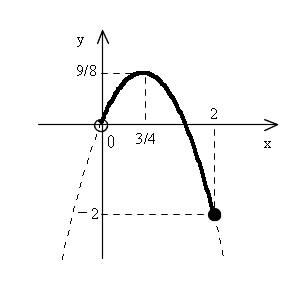
グラフだけから読み取れる最大値と最小値はどうなっていますか？
　\(\displaystyle x=\frac{3}{4}\)　のとき最大値　\(\displaystyle \frac{9}{8}\),
　\( x=2\)　のとき最小値　\( -2\)　だとわかりますよね？
これは
　\( y=-2x^2+3x　（\color{red}{ 0 < x ≦2}　）\)
のグラフを書いただけです。

記述式でグラフは手書きになるので、大小さえはっきりさせ、放物線と認識できれば大丈夫ですよ。
もちろん、マークシート方式の試験でも自分で書くときは大小がわかるように書き出すことは重要です。

２次関数を見たら平方完成
最大最小問題はグラフを読み取る

ということを忘れないで下さい。

⇒　２次関数の最大値最小値問題の解き方

こちらが入試の基本レベルになります。