空間ベクトルでは1つの点からある平面に垂線を下ろしたときの交点を求める問題が良く出題されます。
平面ベクトルでは、点と直線との交点になりますが求め方としては同じです。
どちらも法線ベクトルが有効ですが、答えが1つだけなのでまずはそれをイメージしておきましょう。
空間ベクトルの出題形式をまず知っておこう
先ずは問題を見てください。
空間内の3点
\( \mathrm{O(0\,,\,0\,,\,0)\,,\,A(1\,,\,0\,,\,0)\,,\,B(1\,,\,1\,,\,1)}\)
を含む平面 \( \alpha\) に、点 \( \mathrm{C(2\,,\,3\,,\,2)}\) から垂線を下ろすとき、
この垂線と平面 \( \alpha\) との交点の座標を求めよ。
気がつきましたか?
図がないのです。
平面図形でも図はないことが多いし、センター試験の数学でもあきらかでしたよね。
共通テストでも変わりません。
「わざと」です。笑
あるとすれば、細部できわどい位置関係になるときくらいでしょう。
これは出題者から図を自分で書くように指示されているようなものです。
共通テストでは数学\(\,\mathrm{ⅠA}\,\)では記述も入りますし、(見送られたけど)
こういった作業をしないと得点しづらくなることは間違いないでしょうね。
逆に、
こういった基本作業ができている人にとっては簡単に思えると思いますよ。
センターが出している「共通テスト」の問題例を見てみたけど誘導があまりない分得点はしにくいかもしれないけど、
問題自体はセンター試験よりかなりレベルは低い感じですね。
(問題文の文字数が多いので即座に意味が取れないと苦戦します。)
しかし、
図を書くにしてもちょっとしたコツがあります。
平面図形ではできるだけ問題の条件に忠実に書くことが正解への近道ですが、
空間では位置関係をだいたいでつかめれば、後は適当で良い、
という見切りをすること。
これをしないと空間の位置関係を正確に図示するなんて、時間の無駄になりますよ。
学校の先生がどう言うかは知りません。
関係ないし、どうでもいい。
もしかしたら図を書くことの重要性さえ触れないのかもしれない。
だけど、これを読んだ人は図の大切さを知っておいてください。
そして、完全な図も必要では無い、ということも知っておいてください。
少しだけも前進できたらそれで良い。
ベクトルを使って垂線と平面との交点を求める方法
もう一度問題を書き出すと、
「 空間内の3点
\( \mathrm{O(0\,,\,0\,,\,0)\,,\,A(1\,,\,0\,,\,0)\,,\,B(1\,,\,1\,,\,1)}\) を含む平面 \( \alpha\) に、
点 \( \mathrm{C(2\,,\,3\,,\,2)}\) から垂線を下ろすとき、
この垂線と平面 \( \alpha\) との交点の座標を求めよ。」
問題の条件を書き出して行きましょう。
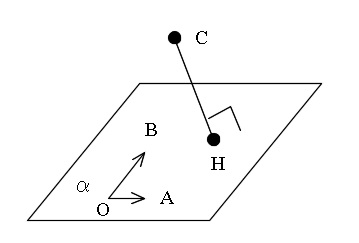
「平面 \( \alpha\) に点\(\,\mathrm{C}\,\)から垂線を下ろす」ということは、
点\(\,\mathrm{C}\,\)は平面 \( \alpha\) 上にはない、ということです。
垂線の方向ベクトルは平面の法線ベクトルと平行です。
平面の法線ベクトルと方程式を求めることはできますが、
平面 \( \alpha\) を \( \overrightarrow{\mathrm{OA}}\,,\,\overrightarrow{\mathrm{OB}}\) を基底として媒介変数表示しましょう。
法線ベクトルと平面の位置関係
垂線と平面 \( \alpha\) との交点を\(\,\mathrm{H}\,\)とすると、点\(\,\mathrm{O}\,\)は原点なので、
\(\begin{eqnarray}
\overrightarrow {\mathrm{OH}}&=&s\, \overrightarrow {\mathrm{OA}}+ t \,\overrightarrow {\mathrm{OB}}\\
&=&s(1\,,\,0\,,\,0)+t(1\,,\,1\,,\,1)\\
&=&(s+t\,,\,t\,,\,t)
\end{eqnarray}\)
と表すことができます。
(個人的には縦ベクトルの方が好きなのですが、、、)
これよりベクトル \( \overrightarrow {\mathrm{CH}}\) は、
\(\begin{eqnarray}
\overrightarrow {\mathrm{CH}}&=&\overrightarrow {\mathrm{OH}}-\overrightarrow {\mathrm{OC}}\\
&=&(s+t\,,\,t\,,\,t)-(2\,,\,3\,,\,2)\\
&=&(s+t-2\,,\,t-3\,,\,t-2)
\end{eqnarray}\)
となり、このベクトルは平面の法線ベクトルのひとつであり、平面に垂直です。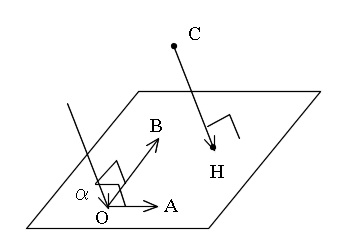
平面に垂直ということは、
「平面上にあるすべてのベクトルと垂直」
ということなので、
\( \overrightarrow {\mathrm{OA}}\,,\, \overrightarrow {\mathrm{OB}}\) とも垂直ということ。
( \( \overrightarrow {\mathrm{AB}}\) とも垂直ですが、文字が2つだから上の2つだけで良いです。)
よって、内積が0になることから、
\(\hspace{10pt} \overrightarrow {\mathrm{OA}}\cdot \overrightarrow {\mathrm{CH}}=0\)
かつ
\(\hspace{10pt} \overrightarrow {\mathrm{OB}}\cdot \overrightarrow {\mathrm{CH}}=0\)
より、(この連立方程式は自分で!)
\(\hspace{10pt}\displaystyle s=-\frac{1}{2}\,,\,t=\frac{5}{2}\)
∴
\(\begin{eqnarray}\displaystyle
\overrightarrow {\mathrm{OH}}&=&(s+t\,,\,t\,,\,t)\\
&=&\left(-\frac{1}{2}+\frac{5}{2} , \frac{5}{2} , \frac{5}{2}\right)\\
&=&\left(2 , \frac{5}{2} , \frac{5}{2}\right)
\end{eqnarray}\)
平面の法線ベクトル、方程式、直線の方程式を利用して解くこともできますが、
ここでは、平面に垂直なベクトルは、平面上のどのベクトルとも垂直、ということを覚えておいて下さい。
空間ベクトルの問題では良く使いますよ。
空間ベクトルの内積の確認
計算をお任せした連立方程式の内積処理をしておきます。
\( \overrightarrow {\mathrm{OA}}=(1\,,\,0\,,\,0)\)
\( \overrightarrow {\mathrm{OB}}=(1\,,\,1\,,\,1)\)
\( \overrightarrow {\mathrm{CH}}=(s+t-2\,,\,t-3\,,\,t-2)\)
なので
\(\hspace{10pt} \overrightarrow {\mathrm{OA}}\cdot \overrightarrow {\mathrm{CH}}=0\\
\Leftrightarrow \hspace{10pt} 1(s+t-2)+0+0\,=0\\
\Leftrightarrow \hspace{10pt} s+t-2\,=0 ・・・②\)
かつ
\(\hspace{10pt} \overrightarrow {\mathrm{OB}}\cdot \overrightarrow {\mathrm{CH}}=0\\
\Leftrightarrow \hspace{10pt} 1(s+t-2)+1(t-3)+1(t-2)\,=0\\
\Leftrightarrow \hspace{10pt} s+3t-7\,=0 ・・・③\)
\(\,②③\,\)より
\(\hspace{10pt}\displaystyle s=-\frac{1}{2}\,,\,t= \frac{5}{2}\)
空間ベクトルの成分での内積(定理)は
\( \vec a=(x_1\,,\,y_1\,,\,z_1)\)
\( \vec a=(x_2\,,\,y_2\,,\,z_3)\)
のとき
\(\hspace{10pt} \large{\color{red}{\vec{a}\cdot \vec{b}=x_1x_2+y_1y_2+z_1z_2}}\)
ですので、内積の定義とともに忘れないようにしておきましょう。
内積の定義と定理
忘れていたらベクトルの問題は解けないと考えて良いです。