判別式は2次方程式に使うものなので関数とは関係ないかというとそうではありません。
2次関数は交点問題になれば連立することですぐに方程式になりますので使えます。
2次不等式では式のままでも解けますが、グラフを利用すると範囲がはっきり見て取れますよ。
2次不等式の解き方
\( a\) を定数とする。
\( x\) についての2次不等式 \( x^2-x+a(1-a) < 0\) を解け。
不等式というと式で処理しようとする高校生が多いですが、ここではグラフで考えることにします。
左辺を \( x\) の関数とみると下に凸なのは分かります。
だから、\( x\) 軸より下になる範囲を探せば良いのですが、\( x\) 軸との交点2つは分かっていません。
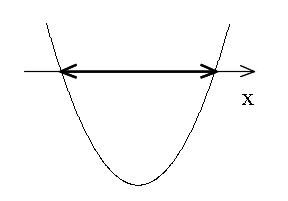
しかしよく見ると、左辺は因数分解出来ます。
このことは誰でもすぐに気がつくわけではありません。
文字が含まれているのでわかりにくいですが、2次方程式や不等式の問題は因数分解出来る問題が多いですから、とりあえず因数分解を試みて下さい。
ダメな場合は?
解の公式です。2次方程式として解の判別も出来ます。
問題を解いてみましょう。
\( x^2-x+a(1-a)\\ \\
=(x-a)\{x-(1-a)\} < 0\)
と左辺は因数分解出来ました。
ここで、\(x\) 軸との交点は \( a\) と \( (1-a)\) なので、この2つで挟めば良いのですが大小がはっきりしていません。
\( a\) と \( (1-a)\) の大小で上限、下限が変わるので場合分けですね。
ⅰ) \( a < (1-a)\) つまり \(\displaystyle a < \frac{1}{2}\) のとき、
\( a < x < (1-a)\)
となります。
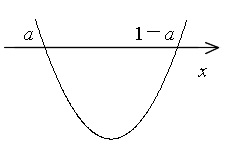
左辺を2次関数としてみたとき \( x\) 軸との交点は、
左(小さい方)が \( a\)
右(大きい方)が \( 1-a\)
ということです。
ⅱ) \( a=(1-a)\) つまり \(\displaystyle a=\frac{1}{2}\) のとき
\( \displaystyle \frac{1}{2} < x < \displaystyle \frac{1}{2}\)
となるので「解なし」です。
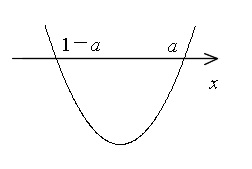
ⅲ) \( (1-a) < a\) つまり \(\displaystyle \frac{1}{2} < a\) のとき
\( (1-a) < x < a\)
ⅰ)ⅱ)ⅲ)をまとめると
\(\displaystyle a < \frac{1}{2}\) のとき \( a < x < (1-a)\)
\(\displaystyle\frac{1}{2} < a\) のとき \( (1-a) < x < a\)
これが問題の2次不等式の解となります。
※
\(\displaystyle a=\frac{1}{2}\) のとき、
\( \left(x-\displaystyle \frac{1}{2}\right)\left(x-\displaystyle \frac{1}{2}\right)=\left(x-\displaystyle \frac{1}{2}\right)^2 < 0\)
となる \(x\) は存在しないことに注意して下さい。
2次関数と直線の交点と判別式の使い方
判別式は「解の判別」なので方程式には使えますが、関数には使えません。
しかし、連立することで方程式になる交点問題は使えます。
\( x\) 軸との交点は \( y=0\) との交点と同じことですよ。
問題です。
放物線C:\(y=x^2-4x+1\) と直線 \( y=mx\) が、
異なる2点で交わるように \( m\) の範囲を決めよ。
いろいろな考え方が出来ますが、判別式利用が一番手っ取り早いでしょう。
\( y=x^2-4x+1\) と \( y=mx\) の交点はこの2つの関数の連立で求まります。
よって、\(y\) を消去した2次方程式
『 \(x^2-4x+1=mx\) が異なる2つの実数解を持てば異なる2点で交わる』
ことになります。
\( x^2-4x+1=mx\\ \\
\Leftrightarrow \hspace{10pt} x^2-(4+m)x+1=0\)
の判別式を \( D\) とすると、\(D > 0\) が求める条件となります。
( \( D ≧ 0\) ではダメです。「異なる」なので重解は不可)
\( D =(4+m)^2-4\\ \\
\hspace{10pt} =m^2+8m+12\\ \\
=(m+2)(m+6) > 0\)
これから
\( m < -6 \hspace{5pt} , \hspace{5pt}-2 < m \)
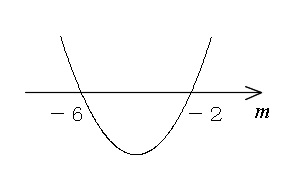
\( D>0\) は軸 \( m\) より上になる部分なので「範囲が分かれる」ことはもう分かりますよね。
グラフで考えるとすると、
\( y=mx\) と \( y=x^2-4x+1\) の位置関係を見なければならないので、
接する場合(重解)を境界に \( y=mx\) の傾きを見ます。
しかし、これは説明が長くなる上(この程度の説明は出来るようになってもらいたいが)ややこしくなるので、やはり判別式利用が得策でしょう。
ちなみに、判別式は『2次方程式』に用いるのであって、2次関数に用いるのではないことは理解しておいてください。
例えばですが、
\( y=x^2-4x+1\) が \( x\) 軸と異なる2つの交点を持つ条件を出すとき、
「判別式を \( D\) とすると、、、」
といきなり書かないようにしましょう。
\( y=0\) つまり \( x^2+(4+m)x+1-0\) の判別式を \(D\) とすると、、、
と「2次方程式に使っている」、と示して下さいね。
ここまできて気がつきました。
判別式について説明をしていなかったようです。
グラフの位置関係まで説明していますので見ておいてください。
ここでも書いていますがグラフを利用するのは不等式でも同じですよ。
