内角の二等分線と外角の二等分線の定理は線分の長さの比についての関係を表しています。
内角の二等分線の性質は覚えておいる人が多いですが、外角については苦手にしている人もいるようなので、覚えやすい方法をお伝えします。
定理の覚え方と使い方は簡単な方法がありますので、覚えて使えるようになっておきましょう。
角の二等分線定理
角の二等分線定理の確認です。
「角の2等分線定理」:
(『角の二等分線による比の移動』のことです。)
内角の二等分線定理
【定理】(内角)
△ABCの∠Aの二等分線と辺BCとの交点Dは、辺BCをAB:ACに内分する。
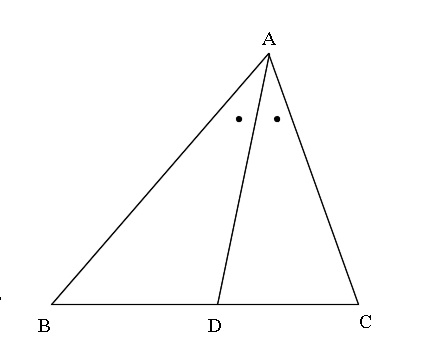
いいかえると、
△ABCの辺BC上の点Dに対し、ADが∠Aを二等分するとき、
\( \color{red}{BD:DC=AB:AC}\)
外角の二等分線定理
【定理】(外角)
△ABCの∠Aの外角の二等分線と辺BCとの交点Dは、辺BCをAB:ACに外分する。
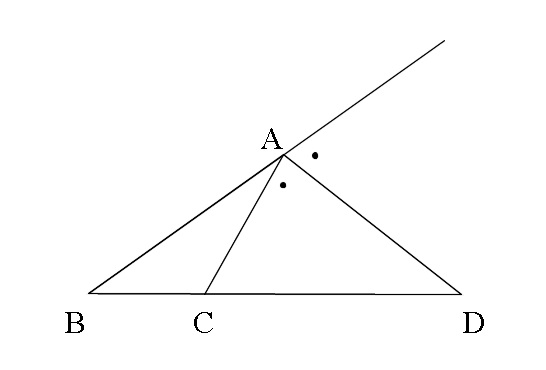
いいかえると、
△ABCの辺BC上の点Dに対し、ADが∠Aの外角を二等分するとき、
\( \color{red}{BD:DC=AB:AC}\)
証明よりも注目しておきたいことがあります。
内角と外角の違いはありますが、点Dの取り方を間違わなければ、
辺の比の関係は同じ式で表されているということです。
点Dは、
「内角の二等分線と対辺との交点」
「外角の二等分線と対辺との交点」
ということをおさえておけばどちらも同じ、
\( \color{red}{BD:DC=AB:AC}\)
ですよね。
内角の2等分線定理は覚えているという人は、外角でも交点をDとすれば同じなので、
先ずは関係式を書き出して、数値を代入してしまえばいいのです。
内分と外分の違いはありますが定理の式だけ見れば同じ!
ちょっと問題を解いてみましょう。
角の二等分線定理を使う問題と解き方
△ABCで、AB=7,BC=6,CA=5とし、
∠Aの二等分線とBCとの交点をD,∠Aの外角の二等分線とBCの延長との交点をEとするとき、
BD,DC,CEの長さをそれぞれ求めよ。
「図形問題で図を書かない人は解く気が無い人」
で得点が低い人の多くの受験生は図を書いていません。
「解く気が無いわけではない」
といっても図を書かないと解けないんだから図を書きましょう。
図形問題のカギは、「図を書く」という作業をきっちりするかしないかです。
定規を持ち込めない大学受験では、出来るだけ問題の条件に忠実な(条件を満たしているような)図を書くように心掛けてください。
余り時間をかけすぎても問題自体を見通す時間がなくなるので普段の練習が大切ですよ。
それと、さりげない数学用語を見落とさないように実際に図を書いていきましょう。
「△ABCで、AB=7,BC=6,CA=5」
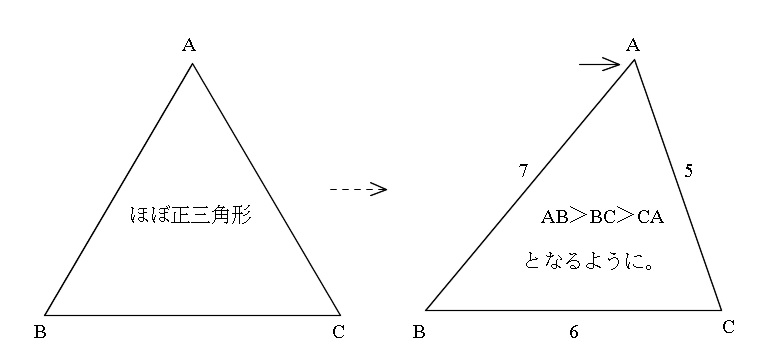
という感じです。
ただし、この問題は外角の二等分線が出てくるので図が大きくなります。
元の三角形を小さくするか、図をかなり大きく書くかのどちらかになります。
「∠Aの二等分線」までを書き込むと、図のような図で納まります。
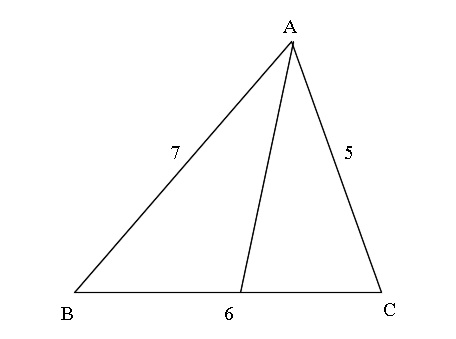
次の、「∠Aの外角の二等分線」です。
外角の二等分線が絡むと図が大きくなりますので解決方法は2つ。
1つは、「外角の二等分線」を見つけたら最初の三角形などを小さめに書く。
もう一つは、縮小した図を書き直す。
問題分の条件の順に書いていくのが普通だと思うので、後者でいいと思いますよ。
おおよその図は出来ているのだから同じような形で書き直すだけなので時間はそれほどかからないですからね。
大きい図の方が見やすいのでスペースが足りると思えば前者のまま書き込んでいきましょう。
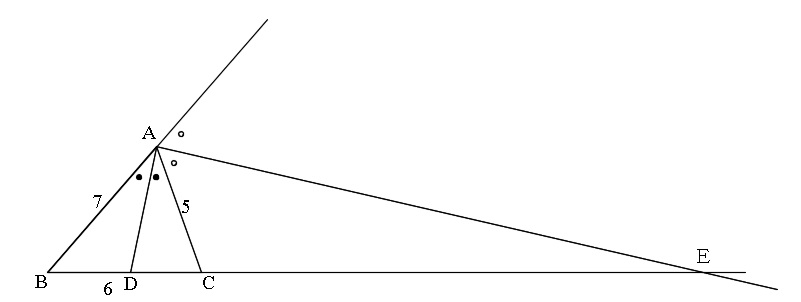
前出の図の大きさでは無理だと判断し縮小させましたが、結構ぎりぎりです。
こんなときはACをわざと短めにすると良いのですが、このまま行きます。
「外角の二等分線」「傍心」と見たら、図を書くとき少し気にしておいてください。
では問題に戻ります。「BD、DC、CEの長さ」ですね。
角の二等分線定理で終わりそうです。
教科書にはあると思うけど外角の二等分線について少し説明しておきます。
ここは読み飛ばしても大丈夫ですよ。
証明方法は1つではありませんので後で確認する程度で、先ずは使えるようになりましょう。
一般性は失われないのでAB>ACとして
△ABCの、
∠Aの外角の二等分線と辺BCとの延長の交点をEとし、
Cを通りAEに平行な線FCを引いて補助すると、
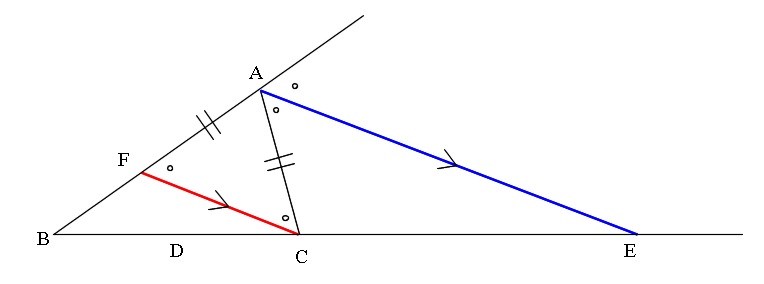
平行線の同位角,錯角から相似が言えて
\( \triangle {BEA} ∽ \triangle {BCF}\)
となるので
\( BE:CE=AB:AF\)
△ACFが二等辺三角形となり \( AF=AC\) であるから、
\( BE:CE=AB:AF\\ \\ \Leftrightarrow \hspace{10pt} BE:CE=AB:AC\)
これは「Eが辺BCをAB:ACに外分する」ことになります。
「平行線を引く」という作業を覚えておけば、
後は「相似」を利用するだけなので公式として覚えていなくても求まりますが、
やはり公式は覚えておくと早いです。
ここまで来れば、問題は簡単です。
二等分線定理より、
\( AB:AC=BD:DC=7:5\)
から
\( BD=6\times \displaystyle \frac{7}{12}=\displaystyle \frac{7}{2}\)
\( DC=6\times \displaystyle \frac{5}{12}=\displaystyle \frac{5}{2}\)
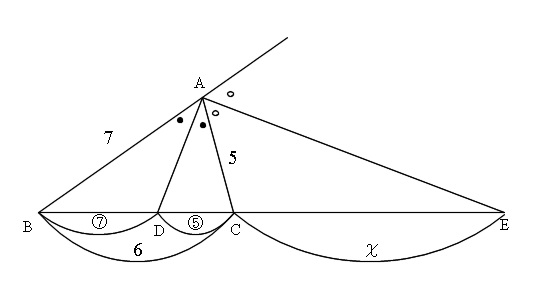
CEには文字を使いましょう。
\( CE=x\) とおくと、\(BE:CE=AB:AC\) だから
\((6+x):x=7:5\)
これを解いて \( x=CE=15\) となります。
図形問題では「相似」が大きく関わってきます。
《高校でも図形はやっているから》と中学の幾何をお粗末にしない方が良いですよ。
「三角比」と「幾何」の融合問題はセンターでもたくさん出てきています。
過去問を見ながらでも良いので、相似がどれだけ重要か確認してみてください。
円に内接する場合も相似はたくさん出てきますよ。
