定積分で求めた面積が文字で表されていて、その最小値を求める問題の解き方です。
最大値、最小値の問題では増減表が活躍しますが、定積分した後に微分するという普通とは順序が逆になるパターンです。
やることはいたって普通のことなので難しく考えず分かることから進めましょう。
定積分と微分
数学\(\,Ⅱ\,\)における微分積分では難しいことはありません。
ここでも「微分⇒積分」ではなく「定積分を行った後に増減表を書く」というように少し順序が違ってきますがやっていることは同じです。
ただ、定数と変数の見分けが苦手な人が多いのでここでも確認しておきましょう。
微分積分の「基本」としては最終確認として見てください。
ここが理解できないということは、基本が欠けているということですのでやり直した方が良いです。
逆に、ここがすぐに納得いくならセンター試験で満点取るくらいの基本は身についているはずですよ。
後は作業をどれだけできるかだけです。
\( a\) は \( 0\,<\, a\,< 1\) を満たす定数とする。
曲線\(\,y=a^2-x^2\,(\,0\,≦\,x\,≦\,1\,)\,\)と\(\,x\,\)軸、
および
2直線\(\,x=0\,,\,x=1\,\)で囲まれた2つの部分の面積の和を\(\,S(a)\,\)とする。
(1) \(S(a)\,\)を求めよ。
(2) \(S(a)\,\)の最小値と,そのときの\(\,a\,\)の値を求めよ。
問題をながめていても意味が分かりにくいということからも、今までの総仕上げ的な問題ですね。
しかし、この手の問題を苦手にする人が多いです。
何故かというと、
図やグラフを書くクセがついていないということもありますが、
\(\,a\,\)が定数だと見切れていないからです。
普通の数字ならできるのに、定数が文字になると分からなくなるのです。
これは数学\(\,\mathrm{ⅠA}\,\)でも同じことが言えますが、定数が文字になっても普通の数字のときと同じように考えれば良いだけなので、いろいろと具体的な数値で試してみると見えてくることが多いですよ。
センターの数学\(\,\mathrm{ⅡB}\,\)では時間的に余裕はありませんので試験中にいろいろ試すことはなかなかできることではありません。
だからそれまでになれておく必要があるので、定数が文字で表された問題は多めの演習をしておくといいでしょう。
最大値最小値問題は図とグラフ
(1)に入る前に条件を図示しておきましょう。
微分積分に限らずこれがないとイメージ出来ません。
「 \( 0\,< \,a\,< \,1\) 」
こういう条件って苦手にしている人多いですよね。
先に考えるから分かり難くなるのです。
\(\hspace{10pt} y=a^2-x^2 \hspace{7pt} (\,0\,≦\,x\,≦\,1\,)\)
を先ずは図示しようとしたとき、
放物線は上に凸だというのは分かりますが\(\,x\,\)軸との交点がどこにあるのか気になります。
そのときに「 \( 0\,< \,a\,< \,1\) 」が効いてくるんです。
\(\hspace{10pt} y=a^2-x^2\,\)は\(\,x\,\)軸と\(\,x=\pm a\,\)で交わります。
定義域が\(\,0\,≦\,x\,≦\,1\,\)なので、\(\,x\,\)軸との交点はその範囲内にある、
ということが \( 0\,< \,a\,< \,1\) から分かるのです。
図示すると図のようになります。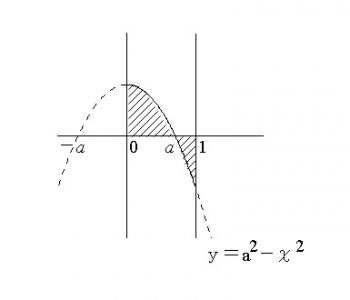
\( x=0\,\)という直線は\(\,y\,\)軸のことです。
つまり \( S(a)\) は図の斜線部の面積を表します。
積分区間が \( 0\,≦\,x\,≦\, a\) と \( a\,≦\,x\,≦\,1\) とに分かれますね。
面積となる積分の方法
(1) \( S(a)\) を求めよ。
面積は「(上の関数)-(下の関数)」の定積分です。
\(x\) 軸は \( y=0\) という直線なので
\(\begin{eqnarray} \displaystyle S(a)&=&\int_{0}^{a} \left\{(a^2-x^2)-(0)\right\}dx +\int_{a}^{1} \left\{(0)-(a^2-x^2) \right\}dx \\ \\
&=&\int_{0}^{a} (a^2-x^2)dx +\int_{a}^{1} (x^2-a^2)dx\\ \\
&=&\left[a^2x- \frac{1}{3}x^3\right]_0^a + \left[ \frac{1}{3}x^3-a^2x\right]_a^1\\ \\
&=&\left(a^3- \frac{1}{3}a^3\right) + \left(\frac{1}{3}-a^2\right)-\left(\frac{1}{3}a^3-a^3\right)\\ \\
&=&a^3-\frac{1}{3}a^3 + \frac{1}{3}-a^2-\frac{1}{3}a^3-a^3\\ \\
&=&\underline{ \frac{4}{3}a^3-a^2-\frac{1}{3} }
\end{eqnarray}\)
増減表の文字
(2) \( S(a)\,\)の最小値と,そのときの\(\,a\,\)の値を求めよ。
これは\(\,S(a)\,\)についての最小値を聞いているので、
もう\(\,x\,\)は関係ありません。
\( S(\color{red}{a})\) は \( \color{red}{a}\) の関数
だということは理解しておいて下さい。
そうすれば、単なる最小値問題で、増減表1つで終わりです。
\(\hspace{10pt} S(a)=\displaystyle \frac{4}{3}a^3-a^2-\displaystyle \frac{1}{3}\)
\(\begin{eqnarray}
S'(a)&=&4a^2-2a\\
&=&2a(2a-1)=0
\end{eqnarray}\)
から \(\displaystyle a=0\,,\,\frac{1}{2}\) なので、
増減表は
\(\,\begin{array}{|c|c|c|c|c|c|c|} \hline
x & (0) &\cdots & \displaystyle \frac{1}{2} & \cdots & (1)\\ \hline
f’(x) & & – & 0 & + & \\ \hline
f(x) & & \searrow & 最小 & \nearrow & \\ \hline
\end{array}\,\)
増減表中の「最小」部分の値は
\(\begin{eqnarray}\displaystyle
S\left( \frac{1}{2}\right)&=& \frac{4}{3}\cdot \left( \frac{1}{2}\right)^3-\left( \frac{1}{2}\right)^2+ \frac{1}{3}\\ \\
&=& \frac{1}{6}- \frac{1}{4}+ \frac{1}{3}\\ \\
&=& \frac{1}{4}
\end{eqnarray}\)
よって、
\(\displaystyle a=\frac{1}{2}\) のとき最小値 \(\displaystyle \underline{ \frac{1}{4} }\)
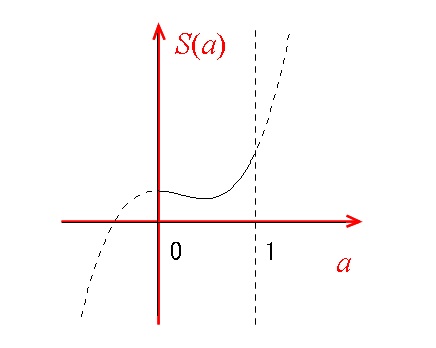
積分(求積)で重要なのは積分区間ですが、やはりグラフですね。
増減表、グラフ、それにちょっとした定理、それで終わりの数学\(\,Ⅱ\,\)の微積です。
ここまで来れば全体の見え方も変わっているのではなでしょうか。
微分法と積分法が逆演算で別々に考えることができない、と言えれば大丈夫です。