高次方程式と高次不等式の解き方と因数の見つけ方

高次方程式と高次不等式の解き方は因数分解などによって次数を下げる方法になります。
因数分解するときの因数の見つけ方は因数定理を使うと便利ですので問題の中で見ておくことにします。
高次方程式と高次不等式では求めるものが違いますのではっきり見分けておきましょう。

高次方程式を因数分解によって解く方法

普段から使っていることですが定理として取り上げておきます。

分かりやすくいうと、
　\( f(x)=0\)　の解全体は、
　\(\hspace{10pt} g(x)=0\,\)の解と\(\,h(x)=0\,\)の解を合わせたもの
だということです。

これは今まで普通に使ってきたことなので難しく考えなくて良いです。

例えば、
　\(\hspace{10pt} (x-1)(x-2)(x-3)=0\,\)の解は、
　\( x-1=0\)　と　\( x-2=0\)　と　\( x-3=0\)　の解を合わせたものだということです。

高次方程式ではこれが基本定理になっていることを確認しました。

では問題を解いて行きましょう。
高次方程式の問題と解き方

高次不等式を解くには高次方程式が解けないと始まりません。
しかし、方程式が解ければ不等式は簡単です。

因数分解しますが、因数定理を利用します。

⇒　剰余の定理（余りの定理）と因数定理の使い方と問題の解き方

（１）左辺を\(\,f(x)\,\)とおくと
　\(\hspace{10pt} f(x)=x^3-x^2-2x+2\)
ここで
　\(\hspace{10pt} \color{red}{f(1)=1-1-2+2=0}\)
となるので
　\(\hspace{10pt}\color{red}{ x-1}\)　を因数にもって
　\(\hspace{10pt} f(x)=(x-1)(x^2-2)\)
と因数分解できます。

この因数分解は　\( x-1\)　で割算すると余りは0になるはずだから商が残りの因数となります。
慣れると割算しなくても因数分解出来るようになりますがミスのないように確実にしましょう。

求める解は、\(\underline{　x=1\,,\,\pm \sqrt{2}　}\)

多項式の係数がすべて整数のときの因数の見つけ方

多項式　\( f(x)=x^n+\cdots +a_0\)　の係数がすべて整数であるとき、
　\( f(x)=0\)　の解　\( \alpha\)　を見つける方法、
つまり、\( x-\alpha\)　を見つける方法ですが、
先ずは「　\( f(x)\)　の定数項の約数　」を両符号調べて下さい。

例えば、
　\( x^3-x^2-2x+2=0\)　を因数定理を使って解こうとするとき、
　\(f(x)=x^3-x^2-2x+2\)　の定数項の約数（\(\,2\,\)の約数：\(\,1\,\)，\(\,2\,\)）、
　\( \pm 1\,,\,\pm 2\)　を調べるということです。

整数係数の方程式が整数解を持たないこともあります。
そのときは違った形の解き方が必要になりますが、入試では一般的な解き方が少ないので約数を試す価値は十分にあります。

最高次の係数が１で無い場合も同じように調べる方法があります。
　\( g(x)=a_nx^n+\cdots +a_0\)　の係数がすべて整数のときは、
　\(\,a_n\,\)の約数を分母、\(\,a_0\,\)の約数を分子、
の組合せを調べます。

例えば、\( g(x)=2x^3-x^2-x-3\)　を因数分解するときは、
\(\,2\,\)の約数（\(\,1\,\)，\(\,2\,\)）が分母、\(\,3\,\)の約数（\(\,1\,\)，\(\,3\,\)）が分子として

　\(\displaystyle \pm \frac{\color{blue}{1}}{\color{red}{1}}\,,\,\pm \frac{\color{blue}{3}}{\color{red}{1}}\,,\,\pm \frac{\color{blue}{1}}{\color{red}{2}}\,,\,\pm \frac{\color{blue}{3}}{\color{red}{2}}\)

を調べて　\( g(x)=0\)　となる　\( x\)　を探します。

（２）方法は（１）と同じです。
左辺を　\( f(x)\)　とおくと
　\(\hspace{10pt} f(x)=x^3-3x^2+4\)

　\( f(-1)=-1-3+4=0\)　となるので　\( x+1\)　を因数にもって
　\(\begin{eqnarray}
f(x)&=&(x+1)(x^2-4x+4)\\
&=&(x+1)(x-2)^2
\end{eqnarray}\)

と因数分解されるので求める解は　\( \underline{　x=-1\,,\,2　}\)

　\( x=2\)　は重解です。
３次方程式は複素数の範囲で重解を含めて３つの解を持ちます。

このように因数定理を用いて因数分解する方法が高次方程式の解き方です。
不等式の解き方を見れば分かりますが、グラフで見れば\(\,x\,\)軸との交点が方程式の解です。

高次不等式の解き方

高次方程式　⇒　グラフ利用

これが１番簡単で分かりやすい解き方です。
ただし、グラフがかけない、ということがないように３次関数のグラフの概形は覚えておくと良いですよ。

例題１では高次方程式でした。
今度は高次不等式ですが、２次不等式の場合どうしていたか思い出して下さい。

例えば、
　\( (x-1)(x-2)>0\)　を解くとき、

　\( (x-1)(x-2)=0\)
を解いて\( x\,＜\,1\,,\,2\,＜\,x\)　とするように、
先に方程式として解いて\(\,x\,\)を求め、それを境界として範囲を求めます。
高次でも境界は必要なので同じように進めて下さい。

例題１で方程式は解いていますので簡単にまとめると、
与不等式の左辺を\(\,f(x)\,\)とおくと

　\(\hspace{10pt} f(x)=(x-1)(x^2-2)\,＞\,0\)

このままでは不等式が解きにくいので\(\,f(x)=0\,\)となる\(\,x\,\)、
つまり、

　\( \color{red}{y=f(x)}\)　としたときの　\( \color{red}{x}\)軸との交点

をすべて出しておけるように因数分解の範囲を広げておきます。

　\( x^2-2=0\)　より　\( x=\pm \sqrt{2}\)
なので実数の範囲まで因数分解の範囲を広げます。

　\(\hspace{10pt} f(x)=(x-1)(x-\sqrt{2})(x+\sqrt{2})\)

よって与不等式は

　\(\hspace{10pt} (x-1)(x-\sqrt{2})(x+\sqrt{2})\,＞\,0\)

となります。

グラフを使った解法が簡単なのですが、先に式の条件で答を出してみます。
じっくり考える時間が無い場合はグラフを使った解法に飛んで良いですよ。

不等式の条件で求める方法

３つの因数について\(\,a\,＜\,b\,＜\,c\,\)とすると

　\(\hspace{10pt}abc\,＞\,0\\
\Leftrightarrow 　a>0\,,\,b>0\,,\,c>0 　または　 a>0\,,\,b < 0\,,\,c < 0\)

３つの数をかけて正になるのは
　\( \color{red}{(+)(+)(+)}\)　か　\( \color{red}{(+)}\color{blue}{(-)(-)}\)
しかあり得ません。

左辺を因数の大きいものから並べると、

　\( (x+\sqrt{2})(x-1)(x-\sqrt{2})\)

となっていることから、この不等式の解は、

　\(\hspace{10pt} (x+\sqrt{2})>0\,,\,(x-1)>0\,,\,(x-\sqrt{2})>0\\ \\
\Leftrightarrow \hspace{10pt}-\sqrt{2}＜ x\hspace{5pt},\hspace{5pt} 1＜ x\hspace{5pt},\hspace{5pt} \sqrt{2}＜ x\\ \\
\Leftrightarrow \hspace{10pt} \sqrt{2}＜ x\)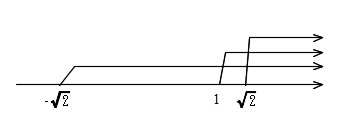
または
　\(\hspace{10pt} (x+\sqrt{2})>0 \hspace{5pt}\,,\,(x-1)＜ 0\,,\,(x-\sqrt{2}) ＜ 0\\ \\
\Leftrightarrow \hspace{10pt}-\sqrt{2}＜ x\hspace{5pt},\hspace{5pt} x＜ 1\hspace{5pt},\hspace{5pt}x＜ \sqrt{2}\\ \\
\Leftrightarrow \hspace{10pt} -\sqrt{2}＜ x ＜ 1\hspace{5pt},\hspace{5pt} \sqrt{2}＜ x\)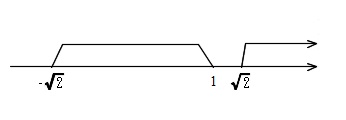となるので

　\( \underline{　-\sqrt{2}\,＜\,x\,＜\,1\hspace{5pt},\hspace{5pt} \sqrt{2}\,＜\,x　}\)

とするのが普通ですが、「または」の結びがわかりにくいです。
（数直線を書いて範囲を見ると難しくはありませんけど。）

グラフを使って高次不等式を解く方法

そこで、３次関数のグラフは３次の係数が正の時、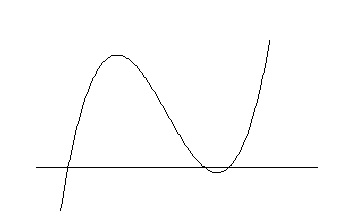図のようになると分かっているので、
\( x\)軸との交点は左から、
　\(\hspace{10pt} -\sqrt{2}\hspace{5pt},\hspace{5pt} 1\hspace{5pt},\hspace{5pt} \sqrt{2}\)

なので\(\,x\,\)軸より上、つまり\(\,(与式)\,＞\,0\,\)となる範囲は、

　\( \underline{　-\sqrt{2}\,＜\,x\,＜\,1\hspace{5pt},\hspace{5pt} \sqrt{2}\,＜\,x　}\)

とすぐに分かるのです。

実数解が３つあるとは限りませんがグラフを利用して構いませんよ。
グラフの増加減少はれっきとした事実です。

（２）は、左辺を因数分解してグラフから見てみましょう。

　\(\hspace{10pt} f(x)=x^3-3x^2+4\)

とすると\(\,f(-1)=0\,\)なので\(\,x+1\,\)を因数にもつことが分かります。

因数分解を進めると、

　\(\begin{eqnarray}
f(x)&=&(x+1)(x^2-4x+4)\\
&=&(x+1)(x-2)^2
\end{eqnarray}\)

このグラフは図の様になるので、（　\( x=2\)　は重解）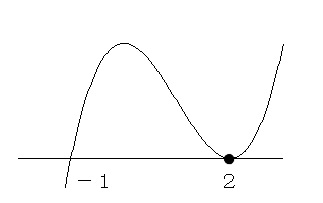
　\(\hspace{10pt}x^3-3x^2+4\,＞\,0\)を満たすのは、
　\( x=2\)　を除外して、

　\( \underline{　-1\,<\,x\,<\,2 \hspace{5pt},\hspace{5pt}2\,<\,x　}\)

（　\( x=2\,\)のときは\(\,x^3-3x^2+4=0\,\)となるので不適。）

問題が、\(\,x^3-3x^2+4\,≧\,0\,\)であれば、
　\(\,x=1\,,\,2\,\)も適するので\(\,-1\,≦\,x\,\)となります。

グラフを利用すれば簡単で、
　高次方程式の解は、\( x\) 軸との交点、
　高次不等式の解は、\( x\) 軸を切り取る範囲、
となりますが、これは２次方程式や２次不等式でも同じですね。

⇒　２次方程式と不等式へのグラフの応用と解き方

グラフを使った解法も立派な解答になるということは忘れないで下さい。

⇒　複素数と方程式の要点

高次方程式の解には複素数がしばしば関係してきますので確認が必要です。