対数不等式の応用問題として表す領域の図示があります。
対数関数における定義と定理がポイントになりますので、
対数の基本の理解度を測るだけでなく、不等式の表す領域の確認にもなります。
ここでは例題をいくつか取り上げて解説しておきますので復習に利用してください。
対数不等式の領域を図示する応用問題のポイント
対数不等式の領域を図示する問題は応用問題としてよく出題されます。
ポイントはいくつかありますが、
問題の意図は対数関数の理解を図ることなので
定義と定理の理解は不可欠です。
基本となる用語の確認は必ずしておきましょう。
対数不等式の領域を図示する方法
例題をいくつか取り上げて解説します。
対数方程式の表すグラフと
不等式の表す領域の図示問題の解き方は基本的には同じです。
方針や方法はこのリンク先ページで解説してあるので、
確認してから読み進めることをおすすめします。
ここでも同じように解説しますが
単なる練習問題として自分でも領域が図示できるようになりましょう。
領域を図示する例題
過去の大学入試問題をベースに例題として取り上げますが、
共通テストのようにムダな日本語は入れません。
数学の基本と応用に関係のない「日本語の読解力の問題か？」
と思えるような部分は省略します。
といっても、大学入試本試験ではムダな日本語は少ないです。
※
難関となる大学の数学では、
シンプルな問題ほど難問の可能性があることは知っておくと良い。
長い文章は時間に猶予のある後期が多いですね。
例題１
最初は解説ページにある、
対数不等式の示す領域の図示の方針が読み取れたかの確認問題です。
の表す領域を図示せよ。
最初に真数条件と対数の条件を見ておきましょう。
\(\hspace{10pt}x＞0\,,\,y＞0\,,\,x \neq 1\,,\,y\neq 1 ･･･①\)
底でも真数でもある\(\,x\,,\,y\,\)が\(\,1\,\)ではないので
\(\hspace{10pt}\log_x y\,,\,\log_y x\)は\(\,0\,\)ではありません。
ここまでは条件探しです。
ここから不等式を処理しに行きます。
不等式にある対数の底をそろえます。
\(\begin{eqnarray}\displaystyle
\log_x y&≦&\log_y x\\
\Longleftrightarrow \log_x y&≦&\frac{\log_x x}{\log_x y}\\
\Longleftrightarrow \log_x y&≦&\frac{1}{\log_x y}
\end{eqnarray}\)
底の変換公式ですよ。
このまま
ⅰ) \(\hspace{4pt}0＜x＜1\,,\,0＜y＜1\)
ⅱ) \(\hspace{4pt}0＜x＜1\,,\,1＜y\)
ⅲ) \(\hspace{4pt}1＜x\,,\,0＜y＜1\)
ⅳ) \(\hspace{4pt}1＜x\,,\,1＜y\)
の場合分けでも良いですよ。（自分でやって見てください。）
ただ、これをやると嫌になるくらい面倒くさく見えますので
不等式の処理の方法を1つ増やしておくと良いです。
ここでは\(\,\log_x y=t\,\)とおきます。
\(\begin{eqnarray}\displaystyle
\log_x y&≦&\frac{1}{\log_x y}\\
\Longleftrightarrow \hspace{30pt}t&≦&\frac{1}{t}
\end{eqnarray}\)
分数のままでは考えにくいので
\(\,t\,\)をかけて処理したいところですが、
\(\,t\,\)は正か負か分かっていません。
そこで\(\,t^2＞0\,\)を両辺にかけます。
（これは\(\,t \neq 0\,\)が分かっているからいえます。）
正の数をかける場合は不等号の向きは変わりません。
\(\begin{eqnarray}\displaystyle
t&≦&\frac{1}{t}\\
t^3&≦&t\\
t^3-t&≦&0\\
t(t^2-1)&≦&0\\
t(t+1)(t-1)&≦&0
\end{eqnarray}\)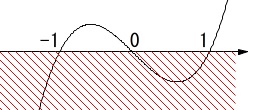
このことから
\(\hspace{4pt}t≦-1\,,\,0≦t≦1\)
対数に戻すと
\(\hspace{4pt}\log_x y≦-1\,,\,0≦\log_x y≦1\)
大小を考えやすくするためにすべてを対数で表します。
\(\hspace{4pt}\log_x y≦\log_x x^{-1}\)
または
\(\hspace{4pt}\log_x 1≦\log_x y≦\log_x x\)
ここで場合分けです。
（\(\,①\,\)の条件は含めて見てください。）
ⅰ)\(\hspace{4pt}0＜x＜1\,\)のとき、（減少関数なので）
真数の大小は逆になります。
\(\hspace{4pt}\displaystyle y≧x^{-1}\hspace{4pt}\Longleftrightarrow \hspace{4pt}y≧\frac{1}{x}\)
または
\(\hspace{4pt}\displaystyle 1≧y≧x\hspace{4pt}\Longleftrightarrow \hspace{4pt}x≦y≦1\)
ここまでを図示しておきます。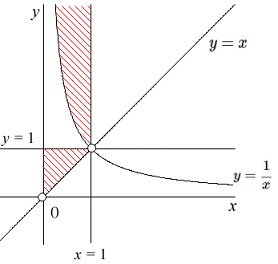
\(\hspace{4pt}0＜x＜1\,\)のときを見ていることを忘れないように。
ⅱ)\(\hspace{4pt}1＜x\,\)のとき、（増加関数なので）
真数の大小はそのままです。
\(\hspace{4pt}\displaystyle y≦x^{-1}\hspace{4pt}\Longleftrightarrow \hspace{4pt}y≦\frac{1}{x}\)
または
\(\hspace{4pt}\displaystyle 1≦y≦x\)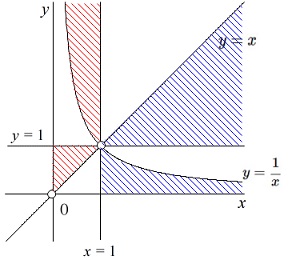
境界は、
\(\hspace{4pt}\displaystyle y=x\,,\,y=\frac{1}{x}\,\)上は含み、
\(\hspace{4pt}\,x\,\)軸、\(\,y\,\)軸および\(\,○\,\)は除外します。
ここまでの不等式の処理ができれば後は同じです。
例題２
今度は方針ページの例題と似た問題です。
の表す領域を図示せよ。
ここは解説は必要ないでしょうから、
解答の書き方ってこんな感じで良い、
というまとめにしておきます。
【解答】
与えられた不等式から
\(\begin{eqnarray}\displaystyle
\hspace{10pt}x＞0\,,\,x \neq 1\,,\,y＞0\,,\,y\neq 1 &･･･&①\\
\log_x y＜2+\frac{3}{\log_x y} &･･･&②\end{eqnarray}\)
を得る。
\(\hspace{4pt}\log_x y=t\,\)とおくと\(\,②\,\)は
\(\hspace{10pt}\displaystyle t\,＜\,2+\frac{3}{t}\)
さらに\(\,t^2\,＞\,0\,\)を両辺にかけて不等式を解くと
\(\begin{eqnarray}\displaystyle
t^3-2t^2-3t\,&＜&\,0\\
t(t+1)(t-3)\,&＜&\,0\\
t\,＜\,-1\,&,&\,0\,＜\,t\,＜\,3
\end{eqnarray}\)
すなわち
\(\hspace{10pt}\displaystyle \log_xy\,＜\,-1\hspace{4pt}\left(\Longleftrightarrow \hspace{4pt}\log_xy＜\log_x \frac{1}{x}\right)\)
または
\(\hspace{10pt}0\,＜\,\log_x y\,＜\,3\hspace{4pt}\left(\Longleftrightarrow \hspace{4pt}\log_x 1＜\log_x y＜\log_x x^3\right)\)
である。（ここは少しおまけしておきました。笑）
ここで底の\(\,x\,\)に注意して、
ⅰ)\(\,x\,＞\,1\,\)のとき
\(\hspace{10pt}\displaystyle y\,＜\,\frac{1}{x}\,,\,1\,＜\,y\,＜\,x^3 ･･･③\)
ⅱ)\(\,0＜x＜\,1\,\)のとき
\(\hspace{10pt}\displaystyle y\,＞\,\frac{1}{x}\,,\,\,1＞\,y\,＞\,x^3 ･･･④\)
\(\,①\,\)かつ\(\,③④\,\)を図示すると下図の斜線部分となる。
ただし、境界は含まない。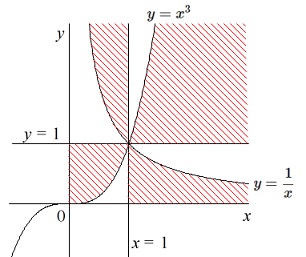
境界は含まないので除外する点を書き込まなくても大丈夫です。
\(\,④\,\)の大小が見にくい時は
\(\hspace{10pt}\displaystyle \frac{1}{x}\,＜\,y\,,\,x^3\,＜\,y\,＜\,1 ･･･④\)
としても良いですよ。
慣れている方で問題ありません。
例題３
今度は２次方程式と対数を合わせた問題の領域になります。
\(\hspace{10pt}x^2-(\log_a b)x+2\log_b a=0\)
が異なる２つの正の実数解をもつような点\(\,(\,a\,,\,b\,)\,\)の動く領域を図示せよ。
ただし、\(\,a\,,\,b\,\)は\(\,1\,\)でない正の実数とする。
対数を定数としているのでここで上げていますが、
方程式中の定数\(\,(\,a\,,\,b\,)\,\)の領域を示す問題は
別のテーマとして取り上げても良いくらいあります。
題意を満たす２次方程式の条件から探っていきます。
「異なる２つの正の実数解を持つ。」
なので２次方程式として条件をまとめて見ましょう。
異なる2つの実数解を持つので
\(\hspace{10pt}x^2-(\log_a b)x+2\log_b a=0\)
の判別式を\(\,D\,\)とすると
\(\hspace{10pt}D\,＞\,0 ･･･①\)
２つの解を\(\,\alpha\,,\,\beta\,\)とすると\(\,\alpha\,,\,\beta\,\)ともに正なので
\(\hspace{10pt}\alpha+\beta\,＞\,0\,,\,\alpha\beta\,＞\,0 ･･･②\)
\(\,①②\,\)を満たすことが条件となります。
\(\,①\,\)から
\(\begin{eqnarray}\displaystyle
D&=&(\log_a b)^2-4\cdot 2\log_b a\\
&=&(\log_a b)^2-\frac{8}{\log_a b}
\end{eqnarray}\)
よって
\(\hspace{10pt}\displaystyle (\log_a b)^2-\frac{8}{\log_a b}\,＞\,0 ･･･③\)
これを処理したくなりますが、
（場合分けがめんどうなので）
もう一つの条件を見ておくと早いです。
\(\,②\,\)から
\(\hspace{4pt}\displaystyle \alpha+\beta\,＞0\hspace{4pt}\Longleftrightarrow \hspace{4pt}\log_a b\,＞\,0 ･･･④\)
\(\hspace{10pt}\displaystyle \alpha\beta\,＞\,0\hspace{4pt}\Longleftrightarrow \hspace{4pt}\frac{1}{\log_a b}\,＞\,0 ･･･⑤\)
\(\,④⑤\,\)から\(\,\log_a b\,＞\,0\)となるので、
\(\,③\,\)は\(\,\log_ab=t\,(\,t\,＞0\,)\)とおくことで
\(\hspace{10pt}\displaystyle t^2-\frac{8}{t}\,＞\,0\)
となりますが\(\,t\,(\,＞\,0\,)\,\)を両辺にかけて
\(\hspace{10pt}\displaystyle t^3\,-8＞\,0\)
これを解くと
\(\hspace{10pt}\displaystyle (t-2)(t^2+2t+4)\,＞\,0\)
ここで\(\,\,t^2+2t+4＞0\,\,\)なので
\(\hspace{10pt}t\,＞\,2 ･･･⑥\)
対数に戻すと
\(\hspace{10pt}\displaystyle \log_ab\,＞\,2\)
両辺を対数にそろえて
\(\hspace{10pt}\displaystyle \log_ab\,＞\,\log_a a^2\)
ここで底の場合分けです。
ⅰ)\(\hspace{4pt}0\,＜\,a\,＜\,1\,\)のとき真数の大小は逆になるので
\(\hspace{10pt}b\,＜\,a^2\hspace{10pt}(\,0\,＜\,a\,＜\,1\,)\)
ⅱ)\(\hspace{4pt}1\,＜\,a\,\)のとき真数の大小はそのままで
\(\hspace{10pt}b\,＞\,a^2\hspace{10pt}(\,1\,＜\,a\,)\)
ⅰ)ⅱ)を図示すると下の図になります。
境界は含みません。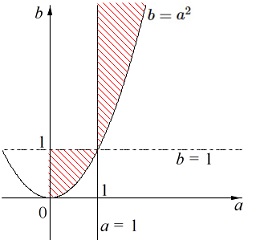
座標軸が\(\,x\,,\,y\,\)ではないことに注意です。
２次方程式の問題として条件を出して行きましたが、
これだけでは２つの解が異符号となる場合行き詰まることがあります。
解と係数の関係は出せますが、
\(\hspace{10pt}\alpha\cdot \beta\,＜\,0\,\)
となるので関係式だけで処理することが困難になることがあります。
（ここでは取り上げません。）
そこで関数として条件を出すことをおすすめします。
２次方程式でしっかり理解している人は分かると思うので
簡単に説明すると方程式の左辺を
\(\hspace{10pt}f(x)=x^2-(\log_a b)x+2\log_b a\)
とおいて2つの解が正となる条件を出します。
見にくいので\(\,\log_ab=t\,\,\)とすると
\(\begin{eqnarray}\displaystyle
f(x)&=&x^2-tx+\frac{2}{t}\\
&=&\left(x-\frac{t}{2}\right)^2-\frac{1}{4}t^2+\frac{2}{t}
\end{eqnarray}\)
ここで条件は異なる２つの解が正となることなので
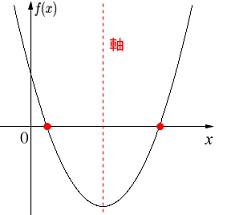となる条件になります。
・軸が正。
・頂点の\(\,f(x)\,\)の値が負。（２つの解を持つ。）
・\(\,f(0)\,\)が正。（軸が正なので解が２つもの正になる。）
を満たせば良いということで足りるでしょう。
ここまでにしておきます。
また気がつけば例題は追加しようと思います。
（たぶん忘れてるけど笑笑）
場合分けでも良いですが
不等式の処理の仕方を覚えてしまえばそれほど煩雑にはなりません。