
「微分・積分」の記事一覧

微分法と積分法の要点(数学Ⅱ)
微分法と積分法の数学Ⅱの範囲の要点のまとめページです。 微分法では導関数や接線の方程式、増減表やグラフ、 積分法においては面積や体積の求め方など重要なポイントがたくさんありますので確認しておいてください。

2020年度センター試験数学2B第2問(微分積分)の解説
2020年(令和2年)度センター試験数学2Bの第2問の解説です。 第2問は2つの放物線と共通接線に関する微分積分の問題です。 前半で共通接線を求め、後半で曲線が囲む面積と最大値を求めます。

極限(lim)の分数式の中にある係数を決定する問題の解き方
極限値を求める問題を解いて行くと、必ずといって良いほど関数の係数を求める問題が出てきます。 数学Ⅱの範囲では数列や三角関数をあつかうのではなく分数の形をした有理関数になります。 ここで説明するのは有理関数の係数の求め方で […]

極限値の求め方(不定形を含む問題も数学Ⅱの範囲で解く方法)
極限値を求める問題の解き方です。極限値の求め方は決まっている訳ではありません。 数学Ⅱの範囲にかぎった整関数と有理関数の問題ですが、簡単なのでいくつか例題を解いておきましょう。 不定形の極限は数学Ⅱではメンドクサイ方法を […]

極限値とは(数学Ⅱ:収束と無限大への発散と不定形について)
数学Ⅱの範囲内での極限値を求める問題を解く以前の説明です。 収束、発散、無限大、不定形、この言葉だけでもお伝えしておきます。 数学Ⅲの内容に触れずに極限値を求めようとする困難な部分が出てきますし、 定義や定理を詳しく説明 […]
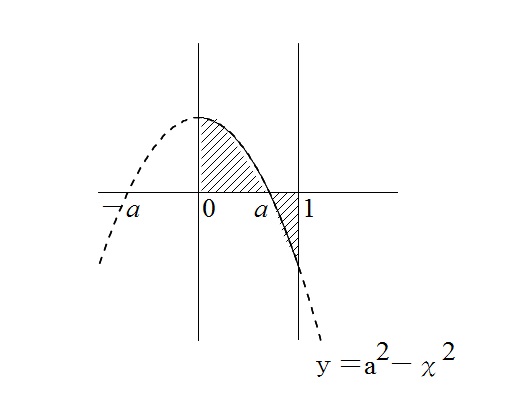
定積分で求めた面積の最小値を求める問題の解き方
定積分で求めた面積が文字で表されていて、その最小値を求める問題の解き方です。 最大値、最小値の問題では増減表が活躍しますが、定積分した後に微分するという普通とは順序が逆になるパターンです。 やることはいたって普通のことな […]
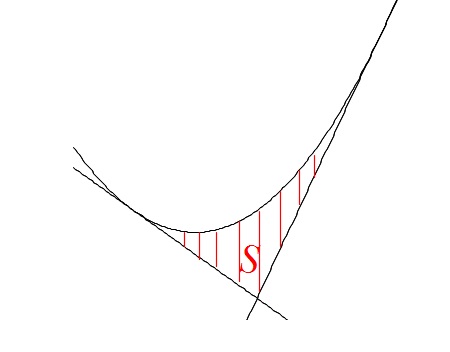
2本の接線と曲線で囲まれる面積の求め方(定積分)
曲線に引いた2本の接線と曲線とで囲まれる面積を定積分で求める問題の解き方です。 ほとんどの問題では接線を求めた後面積を求めるという誘導になります。 接線を求める微分の段階と、面積計算ができるかという積分との二段階の問題に […]
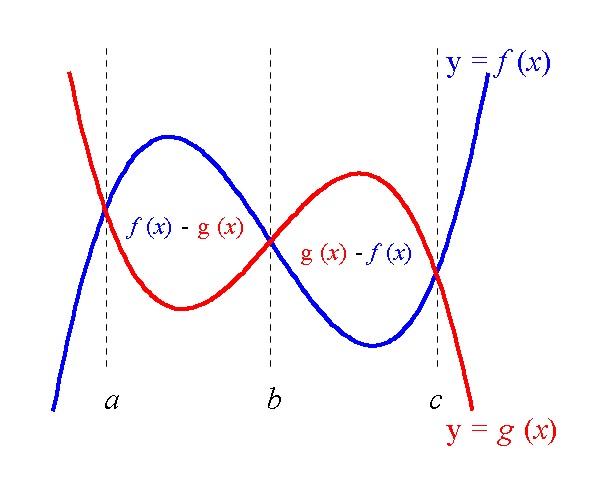
定積分によって面積を求める問題の解き方と公式
面積を求める問題の求め方はいろいろとありますが、定積分もその1つです。 関数で「囲まれる」面積を求める問題はすべてが定積分を使うといって良いでしょう。 ここでは定積分を使って面積を求める基本問題の解き方とちょっと便利な公 […]

関数の中に定積分を部分的に含む関数の求め方とポイント
関数の中に定積分が項として部分的にある関数の求める問題と求め方のポイント、解き方を説明します。 高校生が特に苦手にしている項目です。 定積分全体が関数という場合は、微分積分法の基本定理で変数の変換によって簡単に求まります […]