絶対値がついた方程式や不等式の解き方です。
絶対値を苦手にしている人は、場合分けが出来ていないことが多いです。
ここでは部分的に、または全体で絶対値記号を含む方程式や不等式の解き方を説明します。
グラフを利用することもできますが、先ずは数直線による場合分けをきっちりできるようになっておきましょう。
絶対値問題を解くときの基本
絶対値記号を外すには、方程式でも不等式でも「場合分け」が基本になります。
場合分けができていない人の特長は、
「数直線を書かない」
ことにあるといっても良いので数直線をきっちり書いて下さい。
絶対値とは、
「数直線上の点に対する原点からの距離」
が定義なので、それだけでも理解度はかなり違って来ますよ。
例題で見ていきましょう。
絶対値を含む方程式
(1) \( 7x+|x-2|=9\)
(2) \( |x|=x^2+x-1\)
関数でグラフを書くときも同じですが、
絶対値の中身が「0」になる数を境界に場合分けをするのが基本です。
(1)では\(\hspace{4pt} x-2=0\hspace{4pt}\)から\(\hspace{4pt}x=2\hspace{4pt}\)が境界になりますので、
\( x\, <\, 2 \)と\( 2\,≦\, x\)に分けられます。
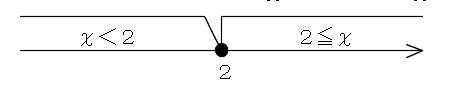
この数直線を書くことで場合分けがしやすくなるのです。
等号(=)は定義域にある場合は、どちらに含めても良いですし、等号だけを別に場合を分けてもいいです。
最終的には「または」で結ぶので同じ結果となります。
場合分けすると、
ⅰ)\(\hspace{4pt}\color{red}{x \,<\, 2}\hspace{4pt}\)の時、
絶対値の中が\(\hspace{4pt}(x-2)\,<\, 0\)(負)なので、
絶対値部分は
\(\hspace{10pt}|x-2|\,=\,\color{red}{-(x-2)}\,=\,2-x\)
方程式は
\(\hspace{10pt}7x+2-x=9\)
となります。
だから\(\hspace{4pt}\displaystyle x=\frac{7}{6}\)
これは\(\hspace{4pt}\color{red}{x \,<\, 2}\hspace{4pt}\)に適しています。

(「 \( x \,<\, 2\) の場合」を見ているのでそれ以外の範囲の解は除外します。)
ⅱ)\(\hspace{4pt}\color{blue}{2 \,≦\, x}\hspace{4pt}\)の時、
絶対値の中が\(\hspace{4pt}(x-2)\,≧\,0\hspace{4pt}\)のときなので
\(\hspace{10pt}|x-2|=\color{red}{x-2}\)
となり、
方程式は
\(\hspace{10pt} 7x+x-2=9\)
だから \(\displaystyle x=\frac{11}{8}\)
となりますが、
これは\(\hspace{4pt} \color{blue}{2 \,≦\, x}\hspace{4pt}\)に不適となります。

(「 \(2 \,≦\, x\) の場合」を見ているのでそれ以外の範囲の解は除外します。)
ⅰ)ⅱ)より、\(\displaystyle x=\frac{7}{6}\)
ⅰ)とⅱ)は範囲を分けて考えているので「または」で結びます。
(2)境界は\(\hspace{4pt}x=0\hspace{4pt}\)です。
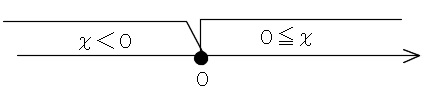
ⅰ)\(\hspace{4pt} x \,<\, 0\hspace{4pt}\)のとき、
\(\hspace{4pt}|x|=-x\hspace{4pt}\)
なので与方程式は、
\(\begin{eqnarray}-x&=&x^2+x-1\\
x^2+2x-1&=&0\\
x&=&-1 \pm \sqrt{5}\end{eqnarray}\)
\(\hspace{4pt} x\,<\,0\hspace{4pt}\)の場合を見ているので
\(\hspace{10pt} x=-1+\sqrt{5}\)は不適
となり、
\( x=-1-\sqrt{5}\)
だけが解となります。
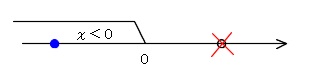
☆ⅰ)の中では\(\hspace{4pt} x\,<\, 0\hspace{4pt}\)と\(\hspace{4pt}x=-1 \,\pm \,\sqrt{5}\hspace{4pt}\)は「かつ」で交わりを見ます。
ⅱ)\(\hspace{4pt}0\,≦\,x\hspace{4pt}\)のとき、
\(\hspace{10pt} |x|=x\)
なので与方程式は、
\(\begin{eqnarray} x&=&x^2+x-1\\
x^2-1&=&0\\
x&=&\pm 1\end{eqnarray}\)
\(\hspace{4pt}0\,≦\,x\hspace{4pt}\)の場合を見ているので、
\(\hspace{10pt} x=-1\hspace{4pt}\)は不適で、
\(\hspace{10pt} x=1\)
だけが適となります。
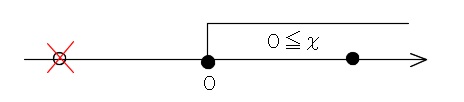
☆ⅱ)の中では\(\hspace{4pt} 0\,≦\,x\hspace{4pt}\)と\(\hspace{4pt} x=\pm 1\hspace{4pt}\)は「かつ」で交わりをみます。
ⅰ)ⅱ)より\(\hspace{4pt} x=-1-\sqrt{5}\hspace{4pt},\hspace{4pt}1\)
☆☆ⅰ)とⅱ)は別々の範囲で見ているので、「または」で適する解を結びます。(要注意です!)
絶対値を含む不等式
次の不等式を解け。
(1) \( |\,2x-1\,| \,<\, x+1\)
(2) \( |\,2x-11\,| \,<\, 5\)
不等式でも等式と同じです。
絶対値の中が0になる値で数直線を区切って場合分けをします。
(1)
\(2x-1=0\hspace{4pt}\)となるのは\(\hspace{4pt}\displaystyle x=\frac{1}{2}\hspace{4pt}\)なので、
\(\displaystyle x \,<\, \frac{1}{2}\hspace{4pt}\)と\(\hspace{4pt}\displaystyle \frac{1}{2} \,≦\, x\hspace{4pt}\)で場合分けします。

ⅰ)\(\hspace{4pt}\displaystyle x\,<\,\frac{1}{2}\hspace{4pt}\)のとき\(\hspace{4pt} 2x-1\,<\,0\)
なので
\(\hspace{10pt} |2x-1|=-(2x-1)\)
で与不等式は
\(\begin{eqnarray} 1-2x\, &<& \,x+1\\
-3x\,&<&\,0 \\
\,0 &<&\,x \end{eqnarray}\)
\(\displaystyle x < \frac{1}{2}\hspace{4pt}\)と「かつ」で結んで、
\(\hspace{10pt}\displaystyle 0\,<\,x\,<\,\frac{1}{2}\)
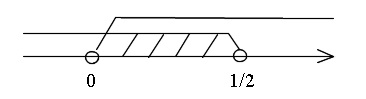
ⅱ)\(\hspace{4pt}\displaystyle \frac{1}{2}≦x\hspace{4pt}\)のとき\(\hspace{4pt} 2x-1\,≧\,0\hspace{4pt}\)
なので
\(\hspace{10pt}|2x-1|=2x-1\)
与不等式は
\(\begin{eqnarray} 2x-1\,&<&\, x+1\\
x \,&<&\, 2\end{eqnarray}\)
\(\displaystyle \frac{1}{2} ≦ x\) と「かつ」で結ぶことになるので
\(\hspace{10pt}\displaystyle \frac{1}{2}\,≦\,x\,<\,2\)
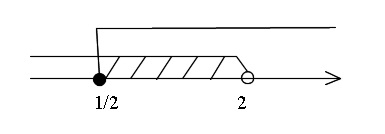
ⅰ)とⅱ)を結ぶと\(\hspace{4pt}\displaystyle x=\frac{1}{2}\hspace{4pt}\)で数直線の範囲がつながり、
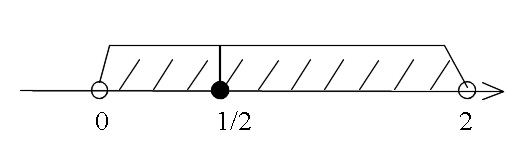
\(\hspace{10pt}\underline{ 0\,<\,x\,<\,2 }\hspace{4pt}\)
が不等式の解となります。
ⅰ)とⅱ)は「または」なので両方が解になります。
場合分けが苦手な人は、数直線をきっちり書いた方が良いですよ。
(2)「\(\hspace{4pt} |2x-11|\,<\,5\hspace{4pt}\)を解きなさい。」です。
\( |\,2x-11\,|\,<\,5\hspace{4pt}\)の絶対値の中が0になる
\(\hspace{10pt}\displaystyle x=\frac{11}{2}\)
を境界に場合分けをします。
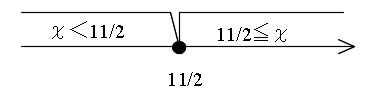
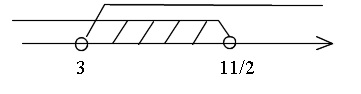
ⅰ)\(\hspace{4pt}\displaystyle x\,<\,\frac{11}{2}\hspace{4pt}\)のとき\(\hspace{4pt} 2x-11\,<\,0\)なので
\(\hspace{10pt} |2x-11|=\color{red}{-(2x-11)}\)
絶対値ははずれます。
与不等式は
\(\begin{eqnarray} -(2x-11)\,&<&\,5\\
-2x\,&<&\,-6\\
3\,&<&\,x\end{eqnarray}\)
\(\displaystyle x\,<\,\frac{11}{2}\hspace{4pt}\)かつ\(\hspace{4pt} 3\,<\,x\hspace{4pt}\)から
\(\hspace{10pt}\displaystyle 3\,<\,x\,<\,\frac{11}{2}\)
ⅱ\(\hspace{4pt}\displaystyle \frac{11}{2} \,≦\, x\hspace{4pt}\)のとき\(\,2x-11\,≦\,0\hspace{4pt}\)なので
\(\hspace{4pt} |\,2x-11\,|=2x-11\)
となり与不等式は
\(\begin{eqnarray} 2x-11\,&<&\,5\\
2x \,&<&\, 16\\
x\,&<&\, 8\end{eqnarray}\)
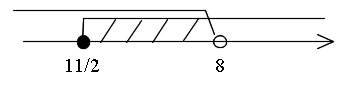
\(\displaystyle \frac{11}{2}\,≦\, x\hspace{4pt}\)かつ\(\hspace{4pt} x\,<\,8\hspace{4pt}\)から
\(\hspace{10pt}\displaystyle \frac{11}{2}\,≦\,x\,<\,8\)
不等式の解は、ⅰ)またはⅱ)の結びとなるなので
\(\hspace{10pt} \underline{ 3\,<\,x\,<\,8 }\)
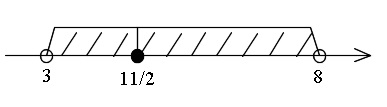
\(\displaystyle x=\frac{11}{2}\) でつながることに注意してください。
絶対値の方程式や不等式はグラフからでも交点をきっちり書いて出すことは出来ます。
グラフのときも場合分けをする要領は同じです。
ただし、グラフが書きにくいときが多いので、場合分けをしっかりできるように数直線を利用しましょう。
絶対値の利用の仕方はこんなのもあります。
ちょっとした手間を惜しんで解けるほど数学の問題は甘くありませんが、
少し手をかけてみると見えてくるものもあります。
ベクトルなどでも絶対値の扱い方は同じです。
数学\(\,Ⅰ\,\)で手を抜いて良いところはありません。
