2次関数の最大値最小値問題は、単純な関数のものと少し違った形のものとがあります。
ここでは変形することによって2次関数の最大最小問題に置きかえられる問題も取り上げておきます。
グラフと判別式のどちらを使うかですが、どちらも使える方が良いですよ。
定義域のある2次関数の最大値最小値問題
\( x\) が集合{ \( x \hspace{5pt} |-1< x< 2 , x\) は実数}の値をとるとき、
\( y=2x^2-4x+1\) の最大値と最小値を求めよ。
2次関数の最大値・最小値問題は平方完成から始まる、といっても良いです。
まずは平方完成しておきましょう。
\( y=2x^2-4x+1\\ \\
=2(x^2-2x)+1\\ \\
=2(x-1)^2-2+1\\ \\
=2(x-1)^2-1\)
丁寧にやりましたが、平方完成出来ないと2次関数の問題は解けない、というくらい重要なので平方完成の練習は十分にしておいてください。
集合{ \( x \hspace{5pt} |-1< x< 2 , x\) は実数}ですが、これは「定義域」を示しているだけです。
\( -1< x< 2\) の範囲で \( y=2(x-1)^2-1\) を見てみると、
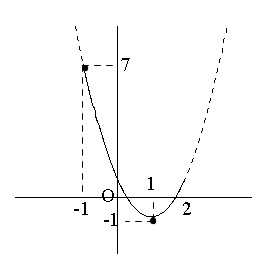
図のようになり定義域が軸を含むので、
最小値は頂点の \(y\) 座標で \( x=1\) のとき \( y=-1\)
最大値は軸から遠い \(x=-1\) のときで \(y=7\)
この2次関数は下に凸なので、
頂点を含めば頂点が最小値、軸から遠い方が最大値、
となります。
( \(x=2\) のときの値は最大最小には関係ないのでグラフには記入していませんが、記入しておいても構いません。)
この問題では定義域に等号がついていますが、等号がついていないとき「最大値はなし」ということもあります。
例えば、\(-1<x<2\) という定義域なら最小値はあるけど、最大値はない。
いずれにしても、「平方完成 → グラフ」はできる限りで書いておくことです。
もちろん、係数に文字がついた場合などは「場合分け」が必要ですよ。
1つランクが上がった問題となります。
先ずは係数に文字のない2次関数の平方完成になれておくことが大切です。
変形することで2次関数として処理できる問題
\( 2x+y=1\) のとき、\(x^2+y^2\) の最小値を求めよ。
\((x,y)\) が \(2x+y=1\) を満たすときの \(x^2+y^2\) の最小値です。
\(y=1-2x\) より
\( x^2+y^2\\ \\
=x^2+(1-2x)^2\\ \\
=\cdots\)
と変形しても良いですが、まずは \(x^2+y^2\color{red}{=k}\) などとおいておくと便利です。
この場合、\(x^2+y^2=k\) は原点中心の円を意味しているので、
\(2x+y=1\) と接するとき \(k\) は最小となるのですが、
今は文字 \(y\) を消去し \(x\) の2次関数として処理しましょう。
平方完成すると
\( k=x^2+y^2\\ \\
=x^2+(1-2x)^2\\ \\
=x^2+1-4x+4x^2\\ \\
=5x^2-4x+1\\ \\
=5 \left(x^2-\displaystyle \frac{4}{5}x \right)+1\\ \\
=5 \left(x-\displaystyle \frac{2}{5} \right)^2-\displaystyle \frac{4}{5}+1\\ \\
=5 \left(x-\displaystyle \frac{2}{5} \right)^2+\displaystyle \frac{1}{5}\)
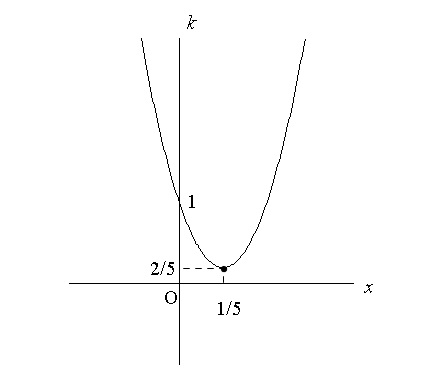
定義域はというと、条件が \(2x+y=1\) なので \(x\) は実数全体となります。
よって \(k\) は頂点で最小となり、\(\displaystyle x=\frac{2}{5}\) のとき最小値 \(\displaystyle \frac{1}{5}\)
図形的な意味は今は考えなくて良いですが、
\( 2x+y=1\) を満たす \((x,y)\) は直線で、
\(k=x^2+y^2\) (円) と交点を持つことが条件となるので、
直線 \(2x+y=1\) と接するとき \( k\) は最小となります。
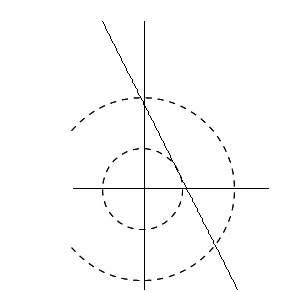
原点中心の円を表す方程式は、
半径を \(r\) とすると、\(x^2+y^2=r^2\) です。
\( k=5x^2-4x+1\\ \\
\Leftrightarrow \hspace{5pt} 5x^2-4x+1-k=0\)
この方程式は実数解を持つはずなので
\( D=4^2-4\cdot 5\cdot (1-k)\\ \\
=4\{4-5(1-k)\}\\ \\
=4(5k-1)≧ 0\)
これから \(\displaystyle k ≧ \frac{1}{5}\) ということはグラフ無しにも出せますね。
特殊な2次関数を普通の2次関数に変える問題
\(x,y\) が実数であり、\(x^2+y^2-2y=0\) をみたすとき、
\(x+y\) の最大値および最小値を求めよ。
例題2とは逆のパターンですね。
1次関数が固定されていません。
これも例題2と同じく、\(x+y\color{red}{=k}\) とおいておきましょう。
そうすれば、\(k\) の最大、最小を探すのと同じことになりますから。
問題は、
\(x^2+y^2-2y=0\) と \(x+y=k\) を同時に満たす \(x,y\) が存在するとき、
\(k\) の最大値、最小値を求めよ。
と同じです。
図形的な意味を考えると、
\(x^2+y^2-2y=0\) は円、\(x+y=k\) は直線なので、
接するときの切片の値ですが、ここでは「2次方程式」として処理しておきます。
\( x+y=k\\ \\
\Leftrightarrow \hspace{5pt} y=k-x\)
これを
\( x^2+y^2-2y=0\)
に代入すると
\( x^2+y^2-2y=0\\ \\
\Leftrightarrow \hspace{5pt} x^2+(k-x)^2-2(k-x)=0\\ \\
\Leftrightarrow \hspace{5pt} 2x^2-2(k-1)x+k^2-2k=0\)
連立しているので交点があるなら、
この2次方程式は実数解を持つことが条件となるので、
判別式をDとすると、
\( D/4=(k-1)^2-2(k^2-2k)\\ \\
=-k^2+2k+1 ≧ 0\)
これは
\(k^2-2k-1≦ 0\) と同じで
\(k^2-2k-1=0\) を満たす \(k\) は \(k=1 \pm \sqrt{2}\) なので
\( k^2-2k-1≦ 0\\ \\
\Leftrightarrow \hspace{5pt} 1-\sqrt{2}≦ k ≦ 1+\sqrt{2}\)
最大値 \(1+\sqrt{2}\)
最小値 \(1-\sqrt{2}\)
\(x^2+y^2-2y=0\) は中心が \((0,1)\)、半径 1 の円
\(y=k-x\) は切片が \(k\) の直線

なので、図から分かるように、接するときの切片が最大最小になります。
単純な2次関数の最大値最小値の求め方
まだの人は見ておきましょう。
これができないと2次関数は始まりません。