組み合わせの考え方は順列と同じ手順をとれば簡単です。
計算公式もありますが、公式で求まるのは部分的な計算だけなので公式を使うことが目的ではありません。
組み分けと道順の数を求める問題を説明しますが、計算方法ではなく考え方や手順を覚えれば順列も組合せも同じ解き方ができます。
組み合わせで使う計算公式
最初に「組合せ」の定義をしておきます。
【定義】
\( n\)個の異なるものから\(r\)個を取り出して組を作るとき、
その1つひとつの組を、\( n\)個のものから\( r\)個とる組合せという。
この組合せの総数を、\( n\)個のものから\( r\)個とる組合せの数といい、
\( \large{\color{red}{_n\mathrm{C}_r}}\) で表す。
\( \mathrm{C}\) は「combination」の頭文字です。
ちなみに順列の \( \mathrm{P}\) は「permutation」の頭文字ですよ。
\( _n\mathrm{C}_r\) の公式:
\( n\)個のものから\(r\)個とる組合せの数 \( _n\mathrm{C}_r\) は
\(\displaystyle \large{\color{red}{_n\mathrm{C}_r=\frac{_n\mathrm{P}_r}{r!}=\frac{n(n-1)(n-2)\cdots (n-r+1)}{r!}}}\)
すなわち
\(\displaystyle \large{\color{red}{_n\mathrm{C}_r=\frac{n!}{r!(n-r)!}}}\)
この公式は文字だけで理解できるほど簡単ではありません。
もちろん覚えなくて良いというわけではありませんが、具体的な数値を入れると一変して簡単になりますので使えるようになっておきましょう。
例えば、
\( _5\mathrm{C}_3=\displaystyle \frac{5\cdot 4\cdot 3}{3\cdot 2\cdot 1}\)
のように、
分子は「左下の数字を先頭に1ずつ小さく右下の数字の数だけ」整数を並べ、
分母は「右下の数字の階乗( \(r!\) )」として整数を並べる、
それだけです。
\( _8\mathrm{C}_2=\displaystyle \frac{8\cdot 2}{2\cdot 1}\)
\( _n\mathrm{C}_2=\displaystyle \frac{n\cdot (n-1)}{2\cdot 1}\)
この公式には基本性質として次の公式も成り立ちます。
① \( \color{red}{_n\mathrm{C}_r=_n\mathrm{C}_{n-r}}\)
② \( \color{red}{_n\mathrm{C}_r=_{n-1}\mathrm{C}_{r-1}+_{n-1}\mathrm{C}_{r}}\)
②は使えなくても問題ありませんが良く証明問題として出されます。
①は計算を楽にするという点からも覚えておきましょう。
\( _n\mathrm{C}_r=\,_n\mathrm{C}_{n-r}\)
これは公式の計算によっても証明できます。
しかし、考え方ですぐに解決するんですよ。
左辺は「 \(n\) 個のものからどの \( r\) 個を取り出すか」ということですが、
これは「 \(n\) 個のものからどの \( n-r\) 個を残すか(取り出さないか)」と同じことですよね。

どのように便利かというと、
\( _8\mathrm{C}_6=_8\mathrm{C}_2\)
ということですが、左辺のまま計算すると
\(\displaystyle _8\mathrm{C}_6=\frac{8\cdot 7\cdot 6\cdot 5\cdot 4\cdot 3}{6\cdot 5\cdot 4\cdot 3\cdot 2\cdot 1}\)
右辺で計算すると
\(\displaystyle _8\mathrm{C}_2=\frac{8\cdot 7}{2\cdot 1}\)
結果は同じですが手間はかなり違います。
公式ですのでバンバン使って良いですよ。
②の証明もしておきましょうか。
飛ばしても大丈夫ですので余裕のある人だけ見ておいてください。
基本だけ見なおしておきたい人は、下の「組合せ」「道順」問題に飛んでも良いです。
先ずは計算による証明です。
\( _{n-1}\mathrm{C}_r+_n\mathrm{C}_{r-1}\\ \\
=\displaystyle \frac{(n-1)!}{(r-1)!(n-r)!}+\displaystyle \frac{(n-1)!}{r!(n-r-1)!}\\ \\
=\displaystyle \frac{r(n-1)!+(n-r)(n-1)!}{r!(n-r)!}\\ \\
=\displaystyle \frac{(n-1)!}{r!(n-r)!} \{r+(n-r)\} \\ \\
=\displaystyle \frac{(n-1)!}{r!(n-r)!} \times n \\ \\
=\displaystyle \frac{n!}{r!(n-r)!}\hspace{10pt} = \hspace{10pt} _n\mathrm{C}_r\)
もう一つ見方を変えることで証明しましょう。
こちらを理解する方が意味は大きいです。
組合せの定義によって
\( n\) 個のものから \( r\) 個とる組合せの総数は \( _n\mathrm{C}_r\) です。
\( n\) 個のもののうち特定の1つに着目すると、
その特定の1つを「含む組合せ」と、「含まない組合せ」が考えられます。
この2つの場合しかありません。
特定の1つを含む場合:
特定の1つはこの\(r\)個のひとつに入り、
特定の1つを除いた \(n-1\) 個の中から「 \( r-1\) 個」選ぶことになるので
\( _{n-1}\mathrm{C}_{r-1}\) 通り。
特定の1つを含まない場合:
特定の1つを除いた \(n-1\) 個の中から「 \( r\) 個」選ぶことになるので
\( _{n-1}\mathrm{C}_r\) 通り。
合わせるとすべての組合せになるので
\( \color{red}{_n\mathrm{C}_r=_{n-1}\mathrm{C}_{r-1}+_{n-1}\mathrm{C}_r}\)
このように順列や組合せには定義からつながる公式がいくつかあります。
余裕ができたら公式とその証明方法を覚えておくと便利なこともありますよ。
ただ、計算で証明できても意味が分からなければ意味はありません。笑
組み分け問題の考え方
12冊の異なる本を次のように分ける。
(1)5冊,4冊,3冊の3組に分ける方法は何通りあるか。
(2)4冊ずつ3人の子供に分けるのは何通りあるか。
(3)4冊ずつ3組に分けるのは何通りあるか。
(4)8冊,2冊,2冊の3組に分ける方法は何通りあるか。
組合せに区別があるかないかの違いを見抜く練習です。
(1)5冊の組み、4冊の組み、3冊の組と区別があります。
12冊から5冊の組を作る方法は \(_{12}\mathrm{C}_5\) ,
残りの7冊から4冊を組む方法は \( _7\mathrm{C}_4\) ,
残り3冊は必然的に決まるので、考えなくて良いのですが、一応書き出すと、
\( _{12}\mathrm{C}_5\times _7\mathrm{C}_4 \times _3\mathrm{C}_3\\ \\
=\displaystyle \frac{12\cdot 11\cdot 10\cdot 9\cdot 8}{5\cdot 4\cdot 3\cdot 2\cdot 1}\times \displaystyle \frac{7\cdot 6\cdot 5\cdot 4}{4\cdot 3\cdot 2\cdot 1}\times 1\\ \\
=27720\)
(答)27720通り。
えらく大きな数字ですがびっくりしないようにして下さい。
これくらいの数字は普通に出てきます。
(2)「4冊ずつ」と見ると区別がないように見えますが、配られる子供に区別があるんです。
子供は区別されますよ。
4冊ずつの組を作って、後で3人に分けても良いですが、はじめから分けた4冊を1人ずつ配ればはやい。
一人目に4冊選ぶ選び方は \( _{12}\mathrm{C}_4\) ,
二人目に4冊選ぶのは \( _{8}\mathrm{C}_4\) ,
もう1人については必然的に残りの4冊となるのですが、
式で書くと \( _{4}\mathrm{C}_4\) (当然1通りです)
よって
\( _{12}\mathrm{C}_4\times _8\mathrm{C}_4 \times _4\mathrm{C}_4\\ \\
=\displaystyle \frac{12\cdot 11\cdot 10\cdot 9}{4\cdot 3\cdot 2\cdot 1}\times \displaystyle \frac{8\cdot 7\cdot 6\cdot 5}{4\cdot 3\cdot 2\cdot 1}\times 1\\ \\
=34650\)
さらに多くなりました。
(答)34650通り。
(3)これは(2)の子供の区別が無くなった場合です。
子どもの順番は「3!」通りあります。
したがって、
\( \displaystyle \frac{_{12}\mathrm{C}_4\times _8\mathrm{C}_4 \times _4\mathrm{C}_4}{3!}\\ \\
=\displaystyle \frac{34650}{3!}\\ \\
=\displaystyle \frac{34650}{3\cdot 2\cdot 1}\\ \\
=5775\)
(答)5775通り。
この(3)については次のような考え方も出来ます。
12冊のうち特定の1冊はどこかの組みに必ず入ります。
その組に入る残り3冊の選び方は、
残り11冊から3冊を選ぶ選び方で、
\( _{11}\mathrm{C}_3\) 通り。
次に残りの8冊のうち特定の1冊は残りのふた組のどちらかに入ります。
その組みに入る残り3冊の選び方は、
残り7冊から3冊を選ぶ選び方で、
\( _{7}\mathrm{C}_3\) 通り。
残りは必然的に組となる4冊。
よって、
\( _{11}\mathrm{C}_3 \times _{7}\mathrm{C}_3\times 1=5775\) 通り
とすることも出来ます。
この考え方も結構使えるのですが、「区別」→「区別をなくす」を基本にしておきましょう。
(4)これは8冊の組は区別されますが、2冊、2冊に分けるふた組が区別されていません。
まずは2冊のふた組を区別して組む方法は、
\( _{12}\mathrm{C}_8 \times _{4}\mathrm{C}_2\times _2\mathrm{C}_2\) です。
2冊2冊の組の区別をなくすと、
\(\displaystyle \frac{_{12}\mathrm{C}_8 \times _{4}\mathrm{C}_2\times _2\mathrm{C}_2}{2!}\\ \\
=\frac{_{12}\mathrm{C}_8 \times _{4}\mathrm{C}_2\times1}{2!}\\ \\
=1485\) 通り。
\( _{12}\mathrm{C}_8\) をそのまま計算(約分)するのは得策ではありません。
\( _{12}\mathrm{C}_8=_{12}\mathrm{C}_4\) と変換しましょう。
\( _n\mathrm{C}_k=\,_n\mathrm{C}_{n-k}\) です。
\( k\) か \( n-k\) が小さい方で計算した方が結果まで早いですよね。
道順問題の解き方
A地点からB地点まで図のような道路がある。
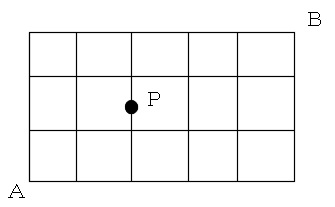
このとき、P地点を通ってA地点からB地点まで行く最短の道順は何通りあるか。
また、P地点を通らずにA地点からB地点まで行く最短の道順は何通りあるか。
「最短の道順」つまり逆戻りはしない、ということです。
前半は、「Pを通って」というのは、下の図のA→Qまで行き、
Pを経由してRまで渡り、R→Bまで進むということです。
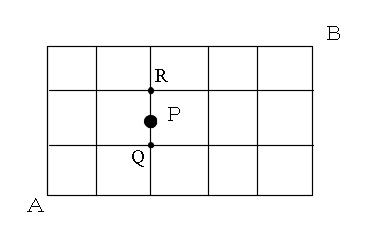
AからQまでの行き方は、右に2つ、上に1つ進む。
つまり、「3つ進むうち、どこで上に1つ上がるか?」
ということと同じです。
もちろん3つのうち横への2つとしても同じで、
\( _3\mathrm{C}_1=_3\mathrm{C}_2\)
○ ○ ○ の3つのうちどの1つを上に進むかの選択だから、
\( _3\mathrm{C}_1=3\) 通り。
QからRへの進み方は1つしかないので考えなくていいです。
そして、RからBへの進み方も、
「上に1つ、横に3つで4つのうちどの1つを上に行くか?」
ということ。
○ ○ ○ ○ のうち1つを選ぶ方法は、\( _4\mathrm{C}_1=4\) 通り。
A→Qのそれぞれに対し、R→Bの選び方があるので、3×4=12通り。
と、ここまではよく見るしそれほど難しくもありません。
後半の「Pを通らず」ですが、
「AからBに行く方法は、「Pを通るか、通らないかのどちらかしかない」
なので、AからBに行く方法すべてから「Pを通る」を引けば良いのです。
AからBへ行く方法は、
「横に5つ、上に3つで、全体で8つ進むうち、どこで上に3つ進むか」
だから、\( _8\mathrm{C}_3=56\) 通り。
(もちろん横の5つの選び方で \( _8\mathrm{C}_5\) としても同じです。)
Pを通るのは12通りなので、Pを通らずAからBに行く方法は、
56-12=44通り。
順列で考えることも出来ますが、
組み合わせ( \( _n\mathrm{C}_k\) )を覚えた後は組み合わせ(選び方)で計算した方が早いですよ。
他にも平行線がいくつもあって、
「平行四辺形をいくつ作れるか?」
のような問題も組み合わせで計算しますよね。アレと同じです。
例
図のように平行線がある。
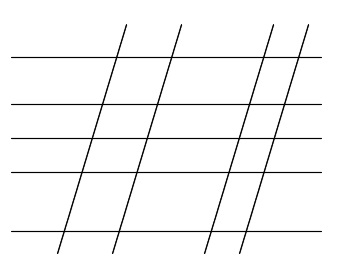
平行四辺形は何種類出来るか。
横に5本、斜めに4本の平行線。
平行四辺形は2組の対辺を平行にすれば出来る。
横5本から2本、斜め4本から2本の平行線を選べば平行四辺形が出来るので、
\( _5\mathrm{C}_2 \times _4\mathrm{C}_2\)
「場合の数」は公式自体は少ないですが問題のパターンが豊富です。
少し時間をかけて演習した方が良いと思いますよ。
順列の基本から確実に解いていきましょう。