順列の中でも公式を持つものに円順列がありますが、この公式は特殊なものではありません。
考え方を変えれば普通の順列ですので問題の解き方も普通に取り組んで大丈夫です。
ただ、取り組み方が公式だけにたよった解き方をしていると数珠順列のような入試レベルでは通用しません。
順列や組合せでも公式は大切です。
筆者も公式はどんどん使うよう勧めています。
しかし、それは数学の問題に取り組む基本的な姿勢、作業ができてからのことです。
数学の成績がイマイチ伸びない、と感じている人は、
基本的な取り組み方からやり直しておいた方が良いかもしれませんよ。
円順列の考え方と公式
例えば家族5人で食事に行ったとして、
円卓に座る方法は何通りあるかを考えてみましょう。
あなた、どこに座りますか?
もちろん円卓という設定は方角やまわりの景色は関係ないということで出題されます。
誰も座っていない状況であなたが最初に座るとして、
イスも同じ、景色も同じなら、どこに座っても同じじゃないですか?
最初に座るのが嫌だとかそういう問題は無しです。
いずれどこかに座るのだから最初に座っても同じでしょう?
つまり、あなたはどこかには座ることになるのだから、
どこに座っても同じということです。
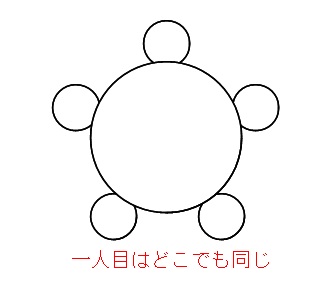
はい、これで1人決まりました。
あなたを、または誰かを円卓のどこかに固定します。
これで残りは4人ですが、
1人決まった円卓の右でも左でもいいから隣から順番に決めていけば、
円になっていなくても同じです。
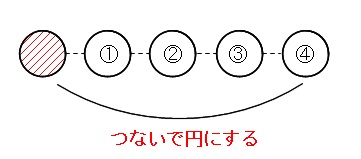
つまり4人を一列に①②③④と並べる順列と同じだということです。
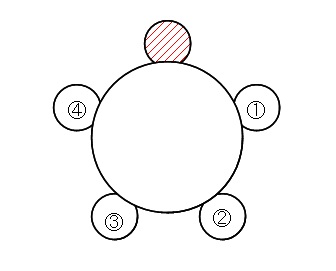
これは人数が \( n\) でも同じことなので円順列の公式が成り立ちます。
\(n\) 個の異なるものを円形に並べて齟齬の順序だけを問題にするとき、
その1つひとつの並び方を \( n\) 個のものの円順列といいます。
【公式】
\(\color{red}{n 個のものの円順列の数は (n-1)! である。}\)
\(a\,,\,b\,,\,c\,,\,d\) の4人が手をつないで輪を作るとき何通りの作り方があるか求めよ。
\( a\) は誰かのとなりになるので、\( a\) を固定すると、
残り3人の順列と同じなので \( 3!=6\) 通り。
円順列の公式に入れると同じく \( (4-1)!=6\) 通り。
男女が隣り合う円順列の問題の解き方
少し練習問題に触れておきましょう。
男子2人,女子3人が円周上に並ぶとき、5人の並び方は何通りあるか。
また、男子2人が隣り合う並び方は何通りあるか。
円順列の基本問題です。
\(n\) 個の円順列は \( (n-1)!\) です。
説明は不要でしょうがもう一度説明しておくと、
1つはどこかにおくので固定しても問題なくて、
残り \(n-1\) 個の順列ということです。
前半は5人の円順列なので、
\((5-1)!=4!=24\) 通りとなります。
男子2人、女子3人の入替は?と思うかもしれませんが、
男子、女子の区別もしていませんし、5人の円順列として見ているので何もしなくて良いです。
人の場合同じ人はいないので区別しておかなければなりません。
しかし、人の場合は元々区別されているのです。
後半は、男子2人は隣り合うので、一度まとめて
「2人を1人と見なし」ます。
すると4人の円順列となり、\( (4-1)=3!\) となります。
この1人とみなした男子2人は入れかわることができるので、
男子の入替 \(2!\) を考えて
\(3!\times 2!=12\) 通り。
「まとまりとみなす」方法は普通の順列でも良く使いますよね。
数珠(じゅず)順列の考え方
この数珠順列は問題によって難しさが極端に変わります。
\(n\) 個の「異なる球」で数珠をつくるときは、
裏返して重なるものがあることを考えて、
円順列 \( (n-1)!\) の半分になることから
\( \displaystyle \frac{(n-1)!}{2}\)
で求まります。
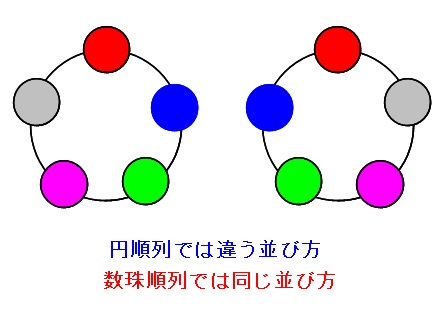
しかし、同じ色の球がある場合、難易度がぜんぜん違う問題に変わります。
赤球6個、白玉4個、黒玉1個がある。
(1)これら全部を円形に並べるとき、並べ方は何通りあるか求めよ。
(2)これら全部を使ってじゅずをつくるとき、作り方は何通りあるか求めよ。
(1)は普通の円順列です。
黒を固定して、残り10個の順列を考えれば良いのです。
ただし、赤球が6個、白玉が4個と同じ色があるので注意しましょう。
\(\displaystyle \frac{10!}{6!\cdot 4!}=\frac{10\cdot 9\cdot 8\cdot 7}{4\cdot 3\cdot 2\cdot 1}=210\) 通り。
問題は(2)です。
これが分かる人はここにいないし、ここにいる人にとってはちょっと難易度が高いと思われますのでパスしても良いですよ。
数珠(じゅず)が問題になったとき、
すべての色が異なるときは半分にする、
異なるときは後回し、
にするのが賢明かもしれません。
(2)
(1)で考えた円順列の対称性に着目し、
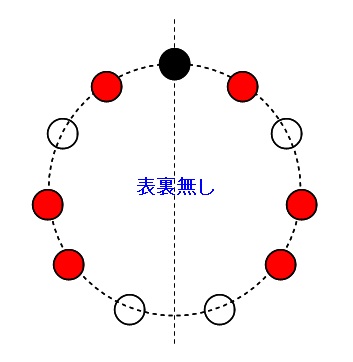
黒玉を通る直線で円順列を真っ二つに割ったとき、
ⅰ)左右が対称なもの
ⅱ)左右が非対称なもの
に分けて考えます。
ⅰ)左右対称な場合
この場合、2つに分けた軸の左か右だけの半分を決めれば並べ方が決まるので、
赤、白の半分、つまり赤3個、白2個の順列の数だけあります。
\( \displaystyle \frac{5!}{3!\cdot 2!}=\displaystyle \frac{5\cdot 4\cdot 3\cdot 2\cdot 1}{3\cdot 2\cdot 1\cdot 2\cdot 1}=10\)
これは裏から見ても同じである「じゅず」として2で割る必要はありません。
もともと半分を決めて対称であるものを計算したので裏から見たものを重ねて数えてはいないからです。
通常「じゅず」は2で割りますが、これがあるため、(1)の答えを2で割った
\( \displaystyle \frac{210}{2}\)
を答えにすると間違いなのです。
ⅱ)左右が対称で無い場合です。
円順列すべては
ⅰ)左右対称
ⅱ)左右非対称
のどちらかに属するので、
ⅱ)の数は「(1)の数」-「ⅰ)の数」となります。
この円順列は(1)とⅰ)から
\( 210-10=200\) 通りあることが分かります。
そしてこの順列は普通に「じゅず」の考え方が成り立ちます。
「裏返して同じになる2つの円順列」
が対になって含まれているので、2つの円順列から同じ数珠ができます。
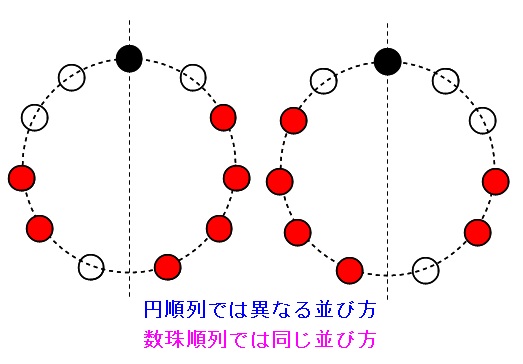
このことからⅱ)の場合にできる数珠は
\(\displaystyle \frac{200}{2}=100\) 通りあり、
左右対称であった数珠ⅰ)と合わせて、
\( 10+100=110\) 通り
が求める数珠の作り方です。
少し説明を簡単にしすぎたかもしれませんガ、
ここが分かるのと分からないのとの違いは大きいのです。
いろいろな場合になれてきているならそれほど難しくは感じないかもしれません。
しかし、場合の数の基本問題をある程度こなしていないと厳しいところです。
ここに手を伸ばすより先にすべきことはあります。
先ずは普通の順列の考え方を身につけてください。