円に接する直線、接線の方程式の求め方です。
円の接線問題には接点となる周上の点が与えられる場合と、円外の点から接線を引く場合があります。
周上の点が接点である場合の求め方は簡単に済ませ、円外の点が与えられている問題の解き方をいくつかの方法でみておきましょう。
周上の接点が与えられている円の接線の方程式
円の接線の方程式を覚えていない人が多いので確認しておきます。
覚えていなくても接線の方程式を求めることはできますが、時間がかかりますので是非覚えておいてください。
中心が原点では無い場合の接線の方程式
円 \( (x-a)^2+(y-b)^2=r^2\) があって
この周上の点 \( (\color{red}{x_1}\,,\,\color{red}{y_1})\) における接線は、
\( (\color{red}{x_1}-a)(x-a)+(\color{red}{y_1}-b)(y-b)=r^2\)
このように書くとわかりにくいようですが、実際に数値を当てはめて2,3題練習すればすぐに使えるようになります。
例えば、
\( (x-3)^2+(y-2)^2\,=5^2\)
は、中心 \( (3\,,\,2)\) , 半径5の円です。
この周上の点 \( (\color{red}{7}\,,\,\color{red}{5})\) における接線は、
\( (\color{red}{7}-3)(x-3)+(\color{red}{5}-2)(y-2)=5^2\)
となりますがこれは、
\( (x-3)^2+(y-2)^2\,=5^2\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} (x-3)(x-3)+(y-2)(y-2)=5^2\)
のように2乗の部分を2つの積に分け、1つの因数部分の \( x\,,\,y\) にそれぞれ円上の点を代入するだけです。
中心が原点の場合の接線の方程式
原点を通る円の場合、中心の座標が \( (a\,,\,b)=(0\,,\,0)\) となるだけなので、
円の方程式は \( x^2+y^2=r^2\) となります。
円 \( x^2+y^2=r^2\) 上の点 \( (\color{red}{x_1}\,,\,\color{red}{y_1})\) における接線は、
\( \color{red}{x_1}x+\color{red}{y_1}y=r^2\)
です。
接点が分かっている場合、即答えが出るので公式として覚えておいてください。
円外の点から接線を引く場合の考え方と解き方3パターン
ここからは例題をみながら進めます。
円 \( x^2-6x+y^2-4y+9\,=0\) の接線のうち、原点を通るものを求めよ。
接点はわかっていませんよ。
接線が原点を通るだけで、原点が接点ということではありません。
接点を設定する方法
「2次関数」でも、「微分」でも分野を問わず、
「接線の問題は接点の設定から」
が基本です。(もちろん例外はあります。)
だから接点がわかっている場合は簡単なんです。
接点を、\( (a\,,\,b)\) とおきましょう。
文字は何でも良いです。
\( x^2-6x+y^2-4y+9=0\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} (x-3)^2-9+(y-2)^2-4+9\,=0\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} (x-3)^2+(y-2)^2\,=4\)
円の問題では、(円かどうか分からない場合も含めて)この変形はしておくと良いです。
センター試験や共通テストのような誘導タイプの問題ではほとんどが「この作業はして当たり前」となっているはずです。
これは中心が \( (3\,,\,2)\) , 半径2の円です。
接点を \( (\color{red}{a}\,,\,\color{red}{b})\) とすると、
接線は \( (\color{red}{a}-3)(x-3)+(\color{red}{b}-2)(y-2)=4\) ・・・☆
となります。
これが「原点を通る」という問題条件があるので、
\((x\,,\,y)\) に \( (0\,,\,0)\) を代入して、
\( (a-3)(0-3)+(b-2)(0-2)=4\\ \\
\Leftrightarrow \hspace{5pt} -3a-2b=-9 ・・・①\)
分からない文字は接点を設定した \( (a\,,\,b)\) の2つあります。
元(文字)が2つなのでもう一つ条件が必要になりますね。
何か使ってない条件は?
そう、接点 \( \color{red}{(a\,,\,b)}\) は円周上の点でもあります。
だから、\( (a\,,\,b)\) を \( (x-3)^2+(y-2)^2\,=4\) に代入して、
\( (\color{red}{a}-3)^2+(\color{red}{b}-2)^2\,=4\) ・・・②
が成り立ちます。
この「条件を探す」クセのついていない人は、接点を設定した時点で②を書き出しておいた方が良いですね。
①②を連立すると、
\( (a\,,\,b)=(3\,,\,0)\,,\,\left(\displaystyle \frac{15}{13}\,,\,\displaystyle \frac{36}{13}\right)\)
これらを接線の方程式☆に代入して、求める接線は、
\( \underline{y=0 \hspace{5pt},\hspace{5pt} 12x-5y=0}\)
重解条件から判別式を利用する方法
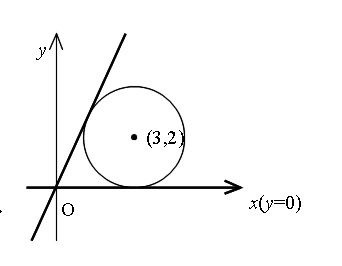
円の中心 \( (3\,,\,2)\) と半径2を図示すると、
\(x\) 軸 \( (y=0)\)
がすぐに接線の1つとわかります。
また、\(y\)軸に平行な \( x=k\) という接線はないこともわかるので、
原点を通ることから接線を \( \color{red}{y=mx}\) とおいて、
\( (x-3)^2+(\color{red}{y}-2)^2\,=4\) と連立して、
\( (x-3)^2+(\color{red}{mx}-2)^2\,=4\\ \\
\Leftrightarrow \hspace{5pt} x^2-6x+9+m^2x^2-4mx+4\,=4\\ \\
\Leftrightarrow \hspace{5pt} (m^2+1)x^2-2(2m+3)x+9=0\)
接する場合は重解となるので、
『重解条件』から判別式 \( D=0\) とする \( m\) を求めます。
\( D/4=(2m+3)^2-(m^2+1)\cdot 9\\ \\
=4m^2+12m+9-9m^2-9\\ \\
=-5m^2+12m\\ \\
=m(-5m+12)=0 \)
これを解いて
\( m=0\,,\,\displaystyle \frac{12}{5}\)
求める接線は
\( ∴ \hspace{7pt} \underline{y=0 \hspace{5pt}, \hspace{5pt} y=\displaystyle \frac{12}{5}x}\)
接点、接線をおくことに重点を置いて説明してみました。
考え方はまだありますが、もう一つだけ試しておきましょう。
点と直線の距離の公式を利用する方法
点と直線の距離の公式(ヘッセ)を使うという方法です。
知ってはいると思いますが公式を書いておきます。
【点と直線の距離】
点 \( (p\,,\,q)\) と直線 \( ax+by+c=0\) との距離 \( d\) は
\(\displaystyle \color{red}{d=\frac{|\,ap+bq+c\,|}{\sqrt{a^2+b^2}}}\)
数学で「距離」とは「最短距離」を意味することは良いですね。
半径は中心と接点までの距離です。
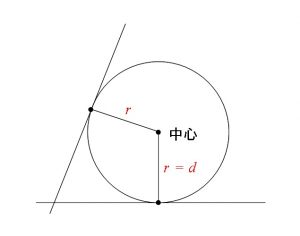
これは中心と接線までの距離のことなのでこの公式が使えます。
求める接線を、原点を通ることから \( ax+by=0\) とおくと
中心 \( (3\,,\,2)\) との距離が半径の2となるので、
\( d=\displaystyle \frac{|\,3a+2b\,|}{\sqrt{a^2+b^2}}\,=2\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} |\,3a+2b\,|\,=2\sqrt{a^2+b^2}\)
両辺平方すると
\( (3a+2b)^2=4(a^2+b^2)\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} 9a^2+12ab+4b^2\,=4a^2+4b^2\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} 5a^2+12ab\,=0\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} a(5a+12b)=0\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} a=0\,,\,5a+12b=0\)
\( a\,,\,b\) がともに0になることはないので、同じ答が出てきます。
※
「\(a=0\,,\,5a+12b=0\)」 のカンマ\(( , )\) は「または」を意味します。
⇒ 数学1A 命題と逆に使う「かつ」と「または」と日常生活の違い
へんな微分を使えば他にも解法は出てきますが、これくらいをイメージできれば大丈夫です。
円の方程式を求める練習は何度もしておきましょう。
⇒ 「3点を通る円」と「2点とある直線上に中心がある円」の方程式の求め方
いろいろな解法が思い浮かぶのは、図やグラフを書いているからですよ。
単元毎のまとめですが全体を見渡しておく方が理解しやすいです。