3次方程式の実数の解の個数問題は、3次関数とx軸との交点の数の問題と言い換えることができます。
整関数である3次関数の微分はかなり計算を楽にしてくれるので多いに利用したいところです。
「3次方程式」と問題に書いてあったとしても方程式として解く必要はありませんよ。
方程式を関数の問題に置きかえる
3次方程式を解く方法として因数定理が有効ですが、
「 方程式 \( x^3-3ax+2=0\) の実数解が1つだけ存在する \( a\) の範囲を求めよ。」
のような問題は解を求めることは要求していません。
\(a\) の値によって解が存在するかどうかも変わってきます。
そこでこの問題を関数の問題に置きかえるのです。
方程式と書いてあろうが関係ありません。
そもそも \( y=f(x)=0\) という方程式は
\( y=f(x)\) と \( y=0\) (\( x\)軸)との交点を求めることと同じことだから意味は同じです。
問題を書き換えます。
関数 \( y=x^3-3ax+2\) のグラフが、
\( x\) 軸と1点のみ共有するような \(a\) の範囲を求めよ。
この関数の問題を解説していきます。
3次関数とx軸との共有点
「単調増加」という言葉を今までに何回か使いました。
増えたり、減ったりがない、「増加し続ける」ことを意味します。
となるとこの問題は、
「単調増加すれば \( x\) 軸とは1点でしか交わらないのではないか?」
とだけ考えてしまってはいけません。
グラフで考えてみましょう。
確かに単調増加すれば、\(x\) 軸とは1点で交わります。

しかし、次のような場合どうでしょう。
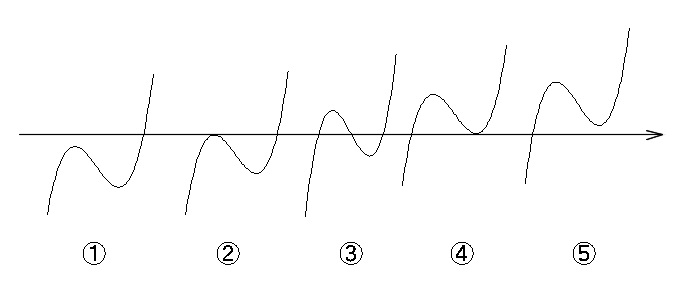
単調増加しない場合でも、①と⑤のグラフは \( x\) 軸と1点でだけ交わっています。
つまり、
「単調増加すれば \( x\) 軸と1点で交わる」
は正しいのですが、
「単調増加しない場合でも \(x\) 軸との交点が1つしかない場合もある」
ということです。
①と⑤は、極大値・極小値を持ち、かつ、それらの極値が同符号である場合です。
場合を分けるとすれば、
ⅰ) 単調増加する場合
ⅱ) 極値を持ち、かつ、それらが同符号の場合
となります。
しかし、この問題に限ってはもう少し簡単に解決します。
関数 \( y=x^3-3ax+2\) において \( y=f(x)\) と表すと
\( f(x)=x^3-3ax+2\)
\( f'(x)=3x^2-3a=3(\underline{x^2-a})\)
ここまでは必須作業です。
これだけでは単調増加か、極値を持つかどうかは分かりません。
ⅰ) \( y=f(x)\) が単調増加するとき、
常に \( \underline{x^2-a}≧ 0\) である必要性から \( a≦ 0\) ・・・①
このとき \(x\) 軸とは1点で交わる。
ⅱ) \( y=f(x)\) が極値を持つとき、\( a \neq 0\) で
\( f'(x)=3x^2-3a=0\) から \( x=\pm \sqrt{a}\) のとき極値を持ち、
\( x=-\sqrt{a}\) のとき極大値、
\( x=\sqrt{a}\) のとき極小値、
となるのですが、
\( f(0)=2\) であることより、極大値は必ず正となります。
何故かというと、
\( x=\pm \sqrt{a}\) の2つの \( x\) は正と負に分かれています。
\( x=-\sqrt{a}\) つまり \( x\) が負側で極大となるので、
\( f(0)=2\) よりは大きいはず。
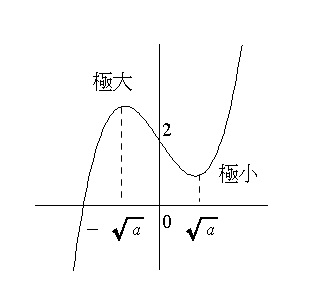
これは式だけ見てても分かりません。
グラフ(または増減表)で確認しているから分かることです。
グラフの概形を書くだけでそれだけのことは分かってくるのですよ。
よって、極小値が極大値の符号と一致することが条件で、
\( f(\sqrt{a})\,>\, 0\) であれば良いのです。
グラフを見ればすぐに分かりますよね。
後はこの条件を求めますが、その前に数学Ⅲを利用できる場合に迷う部分をお伝えしておきます。
定数分離ができる解の個数の求め方
例えば、
「 \( x^3-3x+1-a=0\) の実数解の個数を求めよ。」
のような問題見たことあるでしょう?
この場合、\( x^3-3x+1=a\) と『定数分離』して、
\( y=x^3-3x+1\) のグラフと、\( y=a\) という定直線との交点の数をグラフから場合分けするんでしたよね。
(略解)
\( y=f(x)=x^3-3x+1\)
とすると
\( f'(x)=3x^2-3\)
\( f'(x)=0\) より \( x=\pm 1\)
また \( f(-1)=3\,,\,f(1)=-1\) より
増減表は
| \( x \) | \( \cdots\) | \( -1 \) | \( \cdots\) | \( 1 \) | \( \cdots\) |
| \( f\,'(x) \) | \( + \) | \( 0\) | \( – \) | \( 0 \) | \( + \) |
| \( f(x) \) | \( \nearrow\) | \( 3 \) | \( \searrow\) | \( -1 \) | \( \nearrow\) |
グラフを書いて定直線の \( y=a\) の一部を書き加えると
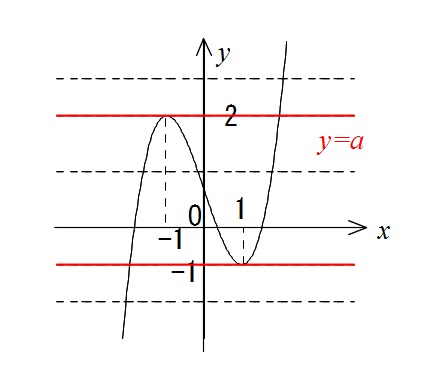
よって
\( a\,< \,-1\,,\,3\, < \,a\) のとき1個
\( a=-1\,,\,3\) のとき2個
\( -1 \,< \,a\, < \,3\) のとき3個
『定数分離』できる場合は、『増減表』と『グラフ』で終わります。
ただし、この定数分離する方法だけで押し通すには数学Ⅲをやっている人しか出来ません。
定数分離しても増減が分からない場合
例題1は数学Ⅲで解くなら定数分離して求まります。
しかし、定数分離以外の方法でも解く方法はあります。
数学Ⅱの範囲で解くには定数分離のように機械的にはできませんが、
極値、増減表、グラフの概形を利用することで対処できます。
もう一度問題を見ておきます。
関数 \( y=x^3-3ax+2\) のグラフが、
\( x\) 軸と1点のみ共有するような \( a\) の範囲を求めよ。
確かに、
「 \( y=x^3-3ax+2\) のグラフが \( x\) 軸と1点のみ共有」
⇔
「 \(x^3-3ax+2=0\) の実数解が1つだけ存在する」
だから、\( x=0\) のときを別に考え、
\( a=\displaystyle \frac{x^3+2}{3x}\)
と分離して
\( f(x)=\displaystyle \frac{x^3+2}{3x}\)
の増減を調べることでも解の個数は考えることができます。
しかし、数学Ⅲの知識がないと増減表、グラフが書けません。
そのため例題1での解答方針の1つとして、
3次関数のグラフで「単調増加」、「極値を持つ場合」、
と場合分けをしたわけです。
では、解答を簡単にですがまとめておきます。
方針は上に示したとおり、場合分けです。
\( y=f(x)=x^3-3ax+2\)
\( y’=f\,'(x)=3x^2-3a=3(\underline{x^2-a})\)
より
ⅰ)\( a\,≦\, 0\) のとき \( \underline{x^2-a\,≧ \,0}\) で
\( y’ \,≧\, 0\) となり単調増加するので \( x\) 軸との共有点は1つ。
ⅱ)\( a> 0\) のとき
\( y’=3(x^2-a)=0\) つまり \( x=\pm \sqrt{a}\) のとき極値を持つ。
ここで
\( x=0\) のとき \( y=2\) ( \( y\) 軸との交点)
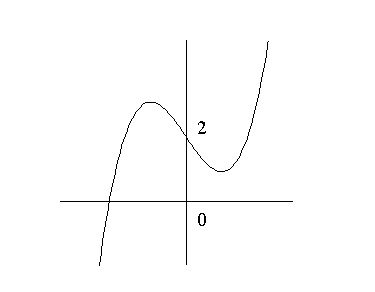
であること、および増減を考えて
\( x=-\sqrt{a}\) で極大
\( x=\sqrt{a}\) で極小
となることから
\(x=\sqrt{a}\) のときの極小値が正であれば \( x\) 軸との共有点は1つになる。
\( x=\sqrt{a}\) のとき
\( f( \sqrt{a} )=(\sqrt{a})^3-3a(\sqrt{a})+2\\ \\
=a\sqrt{a}-3a\sqrt{a}+2\\ \\
=-2a\sqrt{a}+2\)
なので
\( -2a\sqrt{a}+2> 0 \Leftrightarrow a\sqrt{a}< 1\)
\( a\,> \,0\) より
\( a^3\,<\, 1 \Leftrightarrow 0 \,< \,a\, < \,1\)
ⅰ)で \( a\,≦\, 0\) のときも \( x\) 軸との共有点は1つだったので、
ⅱ)と合わせることで
\( \underline{\underline{a \,< \,1}}\)
ちなみに、
「 \( y=x^3-3ax+2\) が \( x\) 軸と共有点が3つ」
や
「 \( x^3-3ax+2=0\) の実数解が3つ」
という問題では、
『 \( f(-\sqrt{a})\cdot f(\sqrt{a})\,<\, 0\) 』
が条件となります。
つまり、
『極大値と極小値が異符号』
で、\( x\) 軸( \(y=0\) )をまたいで存在するということです。
数学Ⅲを意識しないなら、直感的で構いません。
必要十分であれば解き方はどんな解法を使っても良いですよ。
マーク式の誘導タイプであれば解法は指定されていますが、マーク式でも「答」だけを穴埋めする場合は解法指定はありません。
できるのであれば自分の得意な分野に置きかえて解けば良いです。
そこまでできるようになれば少なくとも苦手というのはないでしょうけど、ある程度の点数は取れるという人でも余り出来ていない場合が多いです。
概形を意識しながら問題に当たるとかなり飛躍できますよ。
グラフを書く手順は数学ⅡでもⅢでも同じです。
