関数の増加減少の様子は増減表とグラフが書ければ示すことができます。
極値があるのかないのかも増減表があればすぐに分かるので「微分」における増減表の重要性はいうまでもありません。
数学Ⅱにおいては整関数に限って調べることになるので数少ない決まった手順で十分です。
増減表とグラフが書ければ良いのですが、関数の増加と減少から説明しておきます。
グラフで直感的につかめたら「増減表」に進んでかまいませんよ。
関数の増加と減少
関数 \( f(x)\) において
\(x\) が増えると \( f(x)\) も増える区間を「増加」する区間といいます。
\( x\) が増えると \( f(x)\) が減る区間を「減少」する区間といいます。
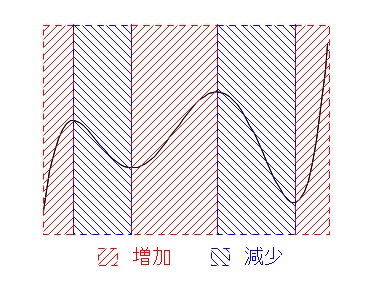
【増加と減少の定義】
関数 \( f(x)\) について、区間 \( I\) に属する任意の \( x_1\,,\,x_2\) に対し、
ⅰ) \( x_1\,< \,x_2 \Leftrightarrow f(x_1) \,< \,f(x_2)\)
が成り立つとき、\( f(x)\) は区間 \(I\) で増加である。
ⅱ) \( x_1\,< \,x_2 \Leftrightarrow f(x_1) \,>\,f(x_2)\)
が成り立つとき、\( f(x)\) は区間 \( I\) で減少である。
という。
簡単にいうと、ある区間で、
どの2つの \( x\) をとっても右にある方が \(f(x)\) が大きいなら増加、
どの2つの \( x\) をとっても右にある方が \(f(x)\) が小さいなら減少、
ということです。
例えば、
\( y=2x\) などの直線はつねに増加しています。
こういう場合を任意の区間で増加、または「単調増加」といいます。
\( y=-3x+2\) は直線ですがつねに減少しています。
こういう場合を任意の区間で減少、または「単調減少」といいます。
「単調」いう言葉は区間ごとに使うことができるので、
区間をいくつかに分けて「その区間で単調」ということができます。
この区間を分けるのに便利なのが \( f'(x)=0\) を解くことです。
この話は後の増減表でします。
その前に微分係数の符号と関数の増加減少について説明しておきます。
微分係数の符号と増加減少
これも直感的で良いです。
【定理】
関数 \( f(x)\) が区間 \( a \,< \,x\,< \,b\) に属するすべての \(x\) に対して、
ⅰ) \( f'(x)\,>\,0\) ならば、\( f(x)\) は \( a \,< \,x\,< \,b\) で増加である。
ⅱ) \( f'(x)=0\) ならば、\( f(x)\) は \( a \,< \,x\,< \,b\) で定数である。
ⅲ) \( f'(x)\,<\,0\) ならば、\( f(x)\) は \( a \,< \,x\,< \,b\) で減少である。
微分係数 \( f'(x)\) は関数 \( f(x)\) の接線の傾きを表しているので、
グラフとにらめっこすれば分かることですが、ちょっと説明しておきます。
例えば、
\( y=x^2\) のグラフを思い出して下さい。
\( y’=2x\) となり、
\( x< 0\) のときは接線の傾きが \( y'< 0\) となり減少、
\( x> 0\) のときは接線の傾きが \( y’> 0\) となり増加、
となっています。
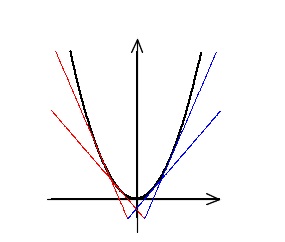
つまり関数が増加するときは接線の傾きは「+」で、減少するときは「-」になっているということです。
正確には、
接線の傾きが負にならなければ増加、
接線の傾きが正にならなければ減少、
ということになるのですが、今はおいておきましょう。
関数と極大値・極小値と増減表
極大値と極小値
極値の定義は省略します。
理由は定義を見ても分からないからです。笑
いや、分かるんですけどややこしいから見なくて良い、という意味でくみ取ってください。
極値を連続な(切れ目のない)グラフで示しておきますので感覚で覚えて下さい。
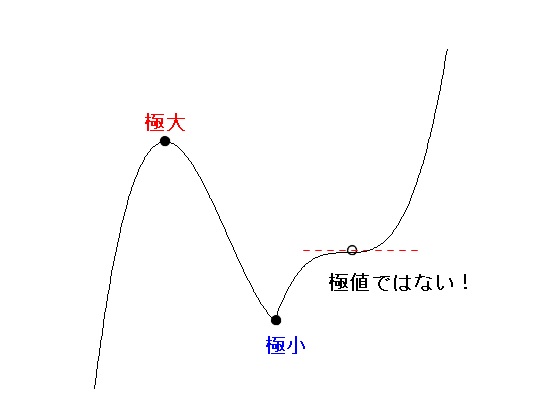
\( f'(x)=0\) の前後で符号が変化しないときは極値ではありません。
極値には「極大値」と「極小値」があります。
増加から減少に変化するときを「極大値」、
減少から増加に変化するときを「極小値」、
といいます。
増減表の書き方
関数の増減をグラフではなく、表で示したものを「増減表」といいます。
数学\(\,Ⅱ\,\)であつかうのは整関数なので、
\(x\) と \( f'(x)\) と \( f(x)\)
について変化を調べれば十分です。
例えば、
\(\hspace{10pt} f(x)=x^3-12x\)
の増減を調べるときは
\(\hspace{10pt} f'(x)=3x^2-12\\
=3(x+2)(x-2)=0\)
から \( x=-2\,,\,2\) のときに \( f(x)\) が変化する可能性があります。
増減表に示すのは
「 \( x\) の区間を分ける \( x\) の値」
と
「 \( f'(x)\) の符号」
と
「 \( f(x)\) の増減と値」
です。
関数 \( f(x)=x^3-12x\) の増減表は
\(\,\begin{array}{|c|c|c|c|c|c|}\hline
x & \cdots & -2 & \cdots & 2 & \cdots \\ \hline
f’(x) & + & 0 & – & 0 & + \\ \hline
f(x) & \nearrow & 16\,(極大) & \searrow & -16\,(極小) & \nearrow \\ \hline
\end{array}\,\)
増減表の書き方はいろいろありますので基本的な手順と共通事項を書いておきます。
① \(f'(x)=0\) を解いて区間を分けます。
② 各区間の\(\, f'(x)\,\)の符号を「+」「-」で書く。
③ 各区間の\(\, f(x)\,\)の増加を\(\displaystyle \,\nearrow\,\) , 減少を\(\displaystyle \,\searrow \,\)で表す。
④ \(\,f(x)\,\)で必要な値を書き込む。
それだけです。
④は「極大」「極小」と添えて書き込んでも良いですが、値だけでもかまいません。
値を書き込まず「最大」「最小」「極大」「極小」とだけ増減表に書き込んだ場合は、
増減表以外のところに値を示しておきましょう。
特に「最大」「最小」の場合は根拠が必要になるので必ず極値など比較した値を書いて下さい。
関数のグラフの書き方
関数のグラフは、直線や2次関数のように形の分かっている場合はいくつかの点を取って概形を表せば形になりますが、
3次関数以上の関数も何とか形は整いますが増減や値があいまいすぎます。
そこで増減表と同じような手順でグラフの書き方をまとめておくことにします。
関数 \(f(x)\) のグラフの書き方は
① 導関数 \( f'(x)\) を求める。
② 導関数 \( f'(x)=0\) となる \( x\) を求め、区間を分けて増減表を書く。
③ 極値を計算し増減表に書き込む。
④ 座標軸を書き、増減表の増減を見ながらグラフの概形を書く。
可能または必要性があるのであれば、④に追加して
⑤ 極値を座標に記入する。
⑥ 座標軸との交点を記入する。
⑦ 定義域(実線)と定義されていない範囲(破線)とを書き分ける。
数学\(\,Ⅱ\,\)の範囲ではこれだけあれば十分でしょう。
ただ、グラフはできるだけ情報を正確に書き込めば
「グラフより」という技が使えます。笑
なので、時間が許せばグラフはていねいに仕上げておくと良いですね。
※
数学\(\,Ⅲ\,\)になると変曲点や漸近線や極限を考えますが、数学\(\,Ⅱ\,\)では必要ありません。
反比例のような分数関数のグラフだけは漸近線が必要です。
関数 \(f(x)=x^3-12x\) のグラフを
①~⑥の手順で書いて見ると
\(\hspace{10pt} f'(x)=3x^2-12\\
=3(x^2-4)\\
=3(x+2)(x-2)=0\)
から\(\,x=-2\,,\,2\,\)なので増減表は
\(\,\begin{array}{|c|c|c|c|c|c|}\hline
x & \cdots & -2 & \cdots & 2 & \cdots \\ \hline
f’(x) & + & 0 & – & 0 & + \\ \hline
f(x) & \nearrow & 16\,(極大) & \searrow & -16\,(極小) & \nearrow \\ \hline
\end{array}\,\)
また座標軸との交点は
\( y\) 軸との交点は \( f(0)=0\)
で原点となっています。
また \( x\) 軸との交点は \( f(x)=x^3-12x=0\) から
\(\hspace{10pt} x^3-12x\\
= x(x^2-12)\\
=x(x-2\sqrt{3})(x+2\sqrt{3})=0\\
\hspace{5pt} \Leftrightarrow \hspace{5pt} x=\pm 2\sqrt{3}\)
グラフは
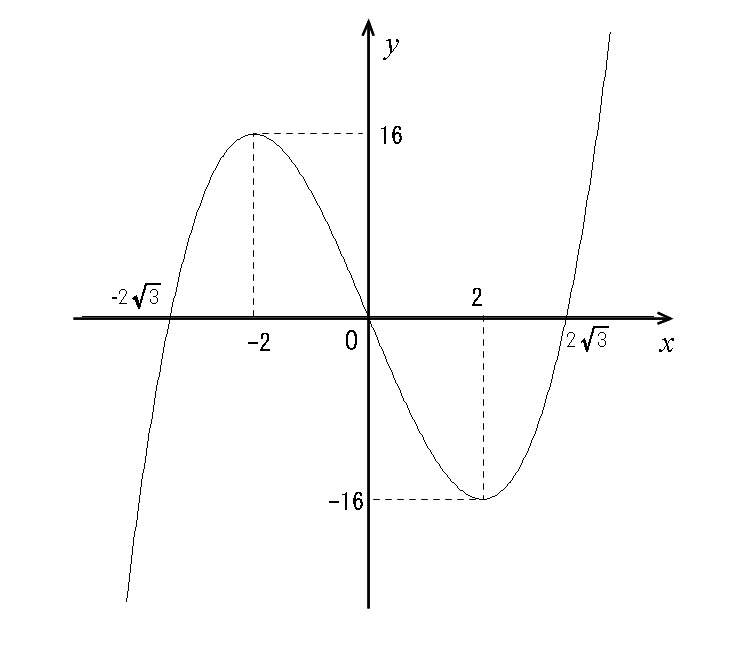
いくつか練習すればグラフを書く手順自体は簡単なのですぐに慣れます。
微分ができないと何もできませんが、増減表が書けるようになると微分は取り組みやすい単元に変わる可能正は大きいですよ。
ちなみにですが、2次関数で増減表を使っても何の問題もありません。
面積を求めるときの積分区間を見分けるにも増減表とグラフは大きな手がかりです。