指数関数と対数関数の要点

指数関数と対数関数の基本内容の要点です。
指数関数と対数関数は逆関数の関係になりますので、一度全体を見通したあとで一つひとつを練習問題を利用して慣れる方が効果的です。
関数なのでグラフが出てきますが形が決まっているので難しくありません。

指数関数や対数関数はコンピューターが発達するとともに計算においては役割が減りました。
しかし、指数や対数の元々の意味から医療分野でも利用されることが多くなり重要な役割を果たしています。

数学\(Ⅱ\)であつかうこの分野は（数学\(\,Ⅲ\,\)に関連する内容を除いて）難しいことはほとんどありませんので、基本だけは徹底しておきましょう。

指数関数

指数はご存じの通り\(\,2^\color{red}{3}\,,\,4^\color{red}{2}\,\)といった累乗数の右上の数のことです。
ここではこの\(\,a^n\,\)という指数を今までより広い範囲で関数として扱うようになります。

指数の拡張

中学までは\(\,a^n\,\)の指数\(\,n\,\)は正の数だけでしたが、
負の数から有理数（分数）、そして実数全体にまで広げます。

ただし、ここから先は底（\(\,a\,\)）を正の数として限定します。

⇒　累乗根と指数の拡張（整数の範囲の指数）

※
整数の範囲（負の数まで）の指数の拡張は別に説明します。
指数関数、対数関数で高校生がこんがらがるのは指数法則は底に限定がありませんが、
関数を扱う上での条件は底が正の数に限られているからです。

指数が自然数の場合の定義から書いておきます。

\(\color{red}{\fbox{　累乗数と底と指数　}}\)

　\(\,n\,\)を自然数とするとき、\(\,n\,\)個の\(\,a\,\)の積
　\(\hspace{10pt}\overbrace{a\times a\times \cdots \times a}^{n}\,\)を\(\,a\,\)の\(\,n\,\)乗といい\(\,a^n\,\)と表す。
　\(\,a^n\,\)において、\(\,n\,\)を「指数」、\(\,a\,\)を「底」という。

「指数」は良いですが「底」という言葉を忘れる人が多いのでしっかり覚えてください。
対数でも使う大切な用語です。

もう一度いっておきますが、ここでは底は正の数だけを考えてください。

\(\color{red}{\fbox{　指数が有理数（実数）の指数法則　}}\)

　\(\,a\,＞\,0\,,\,b\,＞\,0\,\)として、\(\,x\,,\,y\,\)を任意の有理数とすると、
　\(\hspace{10pt}\displaystyle \color{red}{a^x\times a^y=a^{x+y}}　･･･①\)
　\(\hspace{10pt}\displaystyle \color{blue}{\frac{a^x}{a^y}=a^{x-y}}　･･･②\)
　\(\hspace{10pt}\displaystyle \color{red}{(\,a^x\,)^y=a^{xy}}　･･･③\)
　\(\hspace{10pt}\displaystyle \color{blue}{(\,ab\,)^x=a^xb^y}　･･･④\)

②は\(\,a^x\div a^y=a^{x-y}\,\)と同じことですよ。
（割り算は逆数のかけ算です。）

実はこの指数法則は実数の範囲まで拡張することができます。

ただ、実数の指数で表される\(\displaystyle \,3^{\sqrt{5}}\,\)などの数を例に取るとややこしくなるので、
対数を扱うまでは有理数に限定した方が分かり易いからです。

根号の使い方

根号を使った数を分数指数に直す関係式は累乗根のページと重複しますが、
分かっていない人が多いのでここでも書いておきます。

\(\color{red}{\fbox{　根号の表し方　}}\)

　 \(\,a\,＞\,0\,\)のとき\(\,a\,\)の正の\(\,n\,\)乗根を\(\,\sqrt[n]{a}\,\)で表す。

\(\,n\,\)が偶数のとき\(\,n\,\)乗根は2つ、奇数のときはただ一つあることは累乗根のページで確認しておいてください。
ここでは\(\,n\,\)乗根の表し方を根号を使うときは、
左上に数字を付けるということを覚えていれば良いです。
※
平方根の\(\,\sqrt{a}\,\)は左上につく\(\,2\,\)が省略されているので気をつけましょう。
　\(\hspace{10pt}\sqrt[2]{a}=\sqrt{a}\)

根号の表し方でのポイントは逆です。
　\(\displaystyle \,\sqrt[n]{a}=a^\frac{1}{n}\,\)
と根号を使わず指数を分数にすることにあります。

指数関数（\(\,y=a^x\,\)）を見てからわかることですが底は正の数です。
根号を使って表すことはないので根号を使わず、指数の形に変えることがポイントなのです。

指数計算も指数方程式もグラフもです。

方針を一つにしてしまうことは例外を捨ててしまう可能性があるので危険ですが、
　「根号を使わず、底は素数に。」
このことを忘れず取り組めば指数関数、対数関数はそれほどいろいろなことを覚えなければならないわけではありません。

\(\color{red}{\fbox{　分数指数の累乗　}}\)

　\(\,m\,,\,n\,\)を自然数とするとき、分数指数の累乗\(\,a^{\frac{m}{n}}\,\)は、
　\(\hspace{10pt}\displaystyle \color{red}{a^{\frac{m}{n}}=(\sqrt[n]{a})^m}\)
　または
　\(\hspace{10pt}\displaystyle \color{red}{a^{\frac{m}{n}}=\sqrt[n]{a^m}}\)
　により定義される。
また、\(\,a^{-\frac{m}{n}}\,\)は
　\(\hspace{10pt}\displaystyle \color{red}{a^{-\frac{m}{n}}=\frac{1}{a^{\frac{m}{n}}}=\frac{1}{(\sqrt[n]{a})^m}=\frac{1}{\sqrt[n]{a^m}}}\)
により定義される。

これは定義なので考えなくても良いですが、根号は分数指数にすれば良いということでもあります。

例えば、\(\,n\,\)乗根の計算公式があります。

　\(\fbox{　n乗根の計算公式　}\)

　\(\hspace{10pt}\displaystyle \sqrt[n]{a}\times \sqrt[n]{b}=\sqrt[n]{ab}\)
　\(\hspace{10pt}\displaystyle \frac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\frac{a}{b}}\)
　\(\hspace{10pt}\displaystyle \sqrt[n]{a^m}=(\sqrt[n]{a})^m\)
　\(\hspace{10pt}\displaystyle \sqrt[n]{\sqrt[m]{a}}=\sqrt[mn]{a}\)
　\(\hspace{10pt}\displaystyle \sqrt[n]{a^nb}=a\sqrt[n]{b}\)

という公式達も必要無くなります。
※
根号の中から分数指数にしていけば成り立つことが分かるので変形してみてください。

ちょっと長い説明になったので大胆にまとめます。
※
細かい理論は学校の先生にでも聞いて下さい。笑

指数の拡張まとめ

\(\,n\,\)乗根の計算は、根号は使わず分数指数に変換する。

底を正の数とすると、指数は実数全体において
　\(\hspace{10pt}\displaystyle \color{red}{a^x\times a^y=a^{x+y}}\)
　\(\hspace{10pt}\displaystyle \color{red}{(a^x)^y=a-{xy}}\)
　\(\hspace{10pt}\displaystyle \color{red}{a^{-x}=\frac{1}{a^x}}\)
が成り立つ。

以上です。

　\(\hspace{10pt}\displaystyle \color{blue}{a^0=1}\,,\,\color{blue}{\frac{1}{a}=a^{-1}}\,,\,\color{blue}{\sqrt[n]{a}=a^{\frac{1}{n}}}\)
ですよ。忘れないでください。

⇒　指数の掛け算や割り算や分数の計算問題の解き方

計算は別のページでも説明しますがここでも見ておいてください。

⇒　指数方程式の解き方

方程式を解く場合も考え方は同じです。

指数および対数のポイントはここだけなので、ここで終わりたいですが一応最後までまとめます。

指数関数

\(\color{red}{\fbox{　指数関数の定義　}}\)
　
　\(\,a\,\)は\(\,a＞0\,\)かつ\(\,a≠1\,\)を満たす定数とする。
　\(\hspace{10pt}\,\color{red}{y=a^x}\,\)　（\(\,x\,\)は任意の実数）
　で表される関数を\(\,a\,\)を底とする指数関数という。

※
何故、底が\(\,a＞0\,\)かつ\(\,a≠1\,\)となるのかは理由がありますが難しく考えなくて良いです。
\(\,a=1\,\)なら\(\,a^x≡1\,\)なので関数として定義するまでもなく、
連続となるのが\(\,a＞0\,\)のときだけだからです。

指数関数のグラフ

底の\(\,a＞0\,\)かつ\(\,a≠1\,\)は
　\(\hspace{10pt}0\,＜\,a\,＜\,1\,　または　\,1\,＜\,a\)
に分けられます。

この底の違いでグラフが2つに分けられます。

　\(\,1\,＜\,a\,\)のとき\(\,y=a^x\,\)のグラフは増加関数です。
点\(\,(\,0\,,\,1\,)\,\)を必ず通り、\(\,x\,\)軸は漸近線で値が\(\,0\,\)以下になることはありません。
\(\,x\,\)が\(\,0\,\)を超えて増加すると急激に増加します。

「指数関数的に増加する」ということがありますがこのことです。

　\(\,0\,＜\,a\,＜\,1\,\)のとき\(\,y=a^x\,\)のグラフは減少関数です。
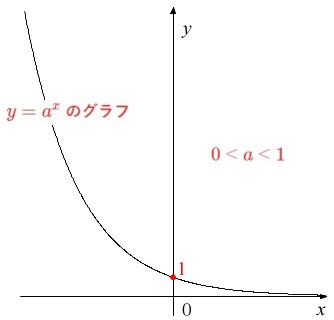\(\,1\,＜\,a\,\)のときと同じように点\(\,(\,0\,,\,1\,)\,\)を必ず通り、
\(\,x\,\)軸は漸近線で値が\(\,0\,\)以下になることはありません。
ただし、\(\,x\,\)が\(\,0\,\)を超えるまでは急激に減少します。

簡単に言えば、\(\,0\,＜\,a\,＜\,1\,\)のグラフと\(\,1\,＜\,a\,\)のグラフは\(\,y\,\)軸対称です。

例えば、\(\,y=2^\color{red}{x}\,\)と\(\,y=\left(\displaystyle \frac{1}{2}\right)^x=2^{\color{blue}{(-x)}}\,\)を見れば明らかに\(\,y\,\)軸対称です。

グラフの概形を見るのはいくつか点を取ればすぐに分かりますが、
ここは考えずに覚えた方が早いです。

　\(\,0\,＜\,a\,＜\,1\,\)　のときは\(\,y=a^x\,\)は減少関数
　\(\,1\,＜\,a\,\)　のとき\(\,y=a^x\,\)は増加関数

それさえ分かれば不等式も指数計算や指数方程式と同じです。

⇒　指数不等式の解き方と指数関数のグラフの利用

指数に関して、方針は一つです。（対数も同じですけど、ちょっとプラス\(\,\alpha\,\)があります。）

対数関数

対数関数は指数関数の逆関数だということが言えれば要点は終わりです。笑

\(\color{red}{\fbox{　対数の定義　}}\)

　\(\,a\,＞\,0\,,\,a\,≠\,0\,\)のとき
　\(\hspace{10pt}\displaystyle \color{red}{p=\log_a{N}　⇔　a^p=N}\)
　\(\,\log_a{N}\,\)に対し、
　\(\,a\,\)を底、\(\,N\,\)を\(\,\log_a{N}\,\)の真数という。

この定義は大切です。
難しい問題ほど定義に戻ることが多いので、覚えておきましょう。

底と真数の位置関係を覚えるのに文字式ではなくて、
　\(\hspace{10pt}\displaystyle \color{red}{2}^\color{blue}{3}=\color{magenta}{8}　⇔　\log_\color{red}{2}{\color{magenta}{8}}=\color{blue}{3}\)
といった一つの具体的な関係を思い出せば良いですよ。

定義を見ればわかりますが、\(\,a^p=N\,\)の\(\,N\,\)は正なので、
真数は必ず正の数でなければなりません。

\(\color{red}{\fbox{　真数条件　}}\)

　\(\,\log_a{N}\,\)における真数\(\,N\,\)は\(\,N\,＞\,0\,\)である。

対数の底に対する条件は指数関数の底の条件と同じです。

後は対数の性質や計算法則をいくつか覚えれば良いだけです。

対数の性質

対数で成り立つ関係式を並べていきます。
対数の法則は指数法則の別表現でしかないので、
指数関数を理解できたら定義に戻ればすぐに分かることなのですべて覚えてください。

底や真数の条件はすべて満たしているものとします。

\(\color{red}{\fbox{　対数の法則　}}\)

　\(\,\color{red}{\log_a{a}=1}\)
　\(\,\color{red}{\log_a{1}=0}\,\)
　\(\,\color{red}{\log_a{xy}=\log_a{x}+\log_a{y}}\)
　\(\,\color{red}{\log_a{(x^m)}=m\,\log_a{x}}\)

真数に（かっこ）を付けましたが、ついていない場合でも同じなので注意してください。
ただし、
　\(\log_a{x^m}=\log_a{(x)^m}\)　と　\(\color{blue}{(\log_a{x})^m}\,\)は違います。

\(\color{red}{\fbox{　対数の法則（続き）　}}\)

　\(\displaystyle \,\color{red}{\log_a{\frac{x}{y}}=\log_a{x}-\log_a{y}}\)
　\(\displaystyle \,\color{red}{\log_a{\frac{1}{x}}=-\log_a{x}}\)

これらは真数を指数に直せば
　\(\hspace{10pt}\displaystyle \frac{x}{y}=x\cdot y^{-1}\,,\,\frac{1}{x}=x^{-1}\)
なので必要無いといえばそれまでです。笑

ここまでの真数\(\,x,y\,\)はすべて正の数です。
例えば、\(\,y=\log_a{x^2}　⇔　y=2\log_a{x}\,\)とできるのは\(\,x＞0\,\)の場合だけです。
\(\,x＜0\,\)のとき、\(\,\log_a{x^2}\,\)は存在しますが、\(\,2\log_a{x}\,\)は存在しません。

\(\color{red}{\fbox{　底の変換公式　}}\)

　\(\,a\,,\,b\,,\,N\)は\(\,1\,\)ではない正の数とする。
　\(\hspace{10pt}\displaystyle \color{red}{\log_a{N}=\frac{\log_b{N}}{\log_b{a}}}\)
　\(\hspace{10pt}\displaystyle \color{red}{\log_a{b}=\frac{1}{\log_b{a}}}\)

教科書では文字が違うかもしれないので書き換えておくと
　\(\hspace{10pt}\displaystyle \color{blue}{\log_a{b}=\frac{\log_c{b}}{\log_c{a}}}\)
　\(\hspace{10pt}\displaystyle \color{blue}{\log_a{b}=\frac{1}{\log_b{a}}}\)
　（\(\,a\,,\,b\,,\,c\,\)は\(\,1\,\)ではない正の数）

証明はしなくて良いですが、定義に戻り
　\(\hspace{10pt}\log_a{b}=x　⇔　a^x=b\)
とおいて両辺を底を\(\,\color{red}{c}\,\)として対数を取ると
　\(\begin{eqnarray}\displaystyle
\log_c{a^x}&=&\log_c{b}\\
x\,\log_c{a}&=&\log_c{b}\\
x&=&\frac{\log_c{b}}{\log_c{a}}
\end{eqnarray}\)

もちろん底\(\,a\,\)は\(\,a≠1\,\)なので\(\,\log_c{a}≠0\,\)です。

この底の変換公式は重要です。
いろいろな底が混じった対数の問題を解く場合、
先ずは「底の統一」が方針になるからです。

⇒　対数の計算公式一覧（底の変換と真数の掛け算・割り算の変形のしかた）

対数方程式や対数不等式の問題はグラフを見た後でやりましょう。

対数関数

対数関数は指数関数の逆関数です。

\(\color{red}{\fbox{　対数関数の定義　}}\)

　\(\,a\,\)を\(\,a\,＞\,0\,,\,a\,≠\,1\,\)を満たす定数とするとき、
　\(\hspace{10pt}y=\log_a{x}\)　（ただし、\(\,x＞0\,\)）
　で表される関数を\(\,a\,\)を底とする\(\,x\,\)の対数関数という。

対数関数のグラフ

指数関数と同じで底の大きさで大きく二つの形になります。

\(\color{red}{\fbox{　関数\(\,y=\log_a{x}\,\)のグラフ　}}\)

　底が\(\,a＞1\,\)のとき
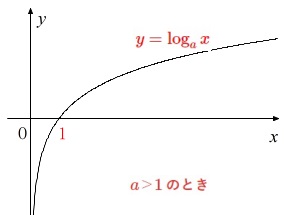定義域は正で、\(\,(\,1\,,\,0\,)\,\)を通り、値域は実数全体の増加関数です。

　底が\(\,0\,＜\,a\,＜\,1\,\)のとき
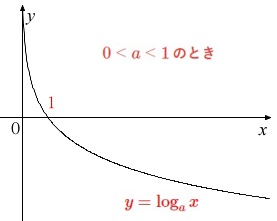定義域は正で、\(\,(\,1\,,\,0\,)\,\)を通り、値域は実数全体の減少関数です。

逆関数なので、
\(\,\color{red}{y=a^x}\,\)のグラフと\(\,\color{blue}{y=\log_a{x}}\,\)のグラフは\(\,y=x\,\)に関して対称です。
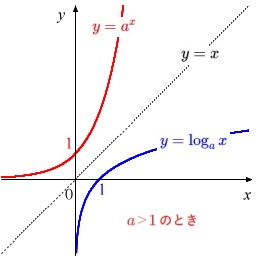底\(\,a\,\)が\(\,0\,＜\,a\,＜\,1\,\)のときも同様です。

底による増加減少が見て取れれば大小関係が理解できます。

\(\color{red}{\fbox{　対数の大小　}}\)

　\(\hspace{10pt}\color{red}{\log_a{P}\,＝\,\log_a{Q}　⇔　P\,=\,Q\,}\)
（等式の場合は真数も等しくなります。）

⇒　対数方程式の解き方と対数関数のグラフの書き方

\(\hspace{10pt}\,a＞1\,\)　のとき
　\(\,\hspace{10pt}\color{red}{\log_a{P}\,＜\,\log_a{Q}　⇔　0\,＜\,P\,＜\,Q\,}\)
（真数の大小は対数の大小そのままです。）
\(\hspace{10pt}\,0\,＜\,a\,＜\,1\,\)　のとき
　\(\,\hspace{10pt}\color{red}{\log_a{P}\,＜\,\log_a{Q}　⇔　0\,＜\,Q\,＜\,P\,}\)
（真数の大小が逆になるということです。）

⇒　対数不等式の解き方と対数関数のグラフの利用

底、真数の条件は真っ先に見ておきましょう。
後は対数法則、底の変換を利用すればほとんど解決します。

⇒　指数関数・対数関数の最大値最小値問題の解き方

指数関数と対数関数の最大値最小値問題もグラフの性質を利用します。

常用対数

底を\(\,10\,\)とする対数を常用対数といいます。

　\(\hspace{10pt}\color{red}{\log_{10}P}\)

桁数が大きな数値を扱うときに常用していました。
※
以前、常用対数の底\(\,10\,\)を省略する書き方をしていた頃がありますが今は書いてください。
底を省略した対数は自然対数といって違った数を表しています。

常用対数表が教科書の巻末にあります。
読み取り方は左の数字が真数の「一の位と小数第\(\,1\,\)位の数」、
上の数字がそれに続く「小数第\(\,2\,\)位」の数です。
　\(\begin{array}{|c|c|c|c|c|} \hline
　数　& \cdots & 2 & \color{blue}{3} & \cdots \\ \hline
\cdots & \cdots & \cdots & \cdots & \cdots \\ \hline
3.9 & \cdots & .5933 & .5944 & \cdots \\ \hline
4.0 & \cdots & .6042 & .6053 & \cdots \\ \hline
\color{red}{4.1} & \cdots & .6149 & \color{magenta}{.6160} & \cdots \\ \hline
4.2 & \cdots & .6253 & .6263 & \cdots \\ \hline
\cdots & \cdots & \cdots & \cdots & \cdots \\ \hline
\end{array}\)
この表で読み取った値は
　\(\hspace{10pt}\log_{10}{\color{red}{4.1}\color{blue}{3}}=\color{magenta}{0.6160}\)
となります。