2次方程式の解と2次関数のx軸との交点はグラフ上では同じものとなります。
この共有点の位置がしばしば問題になりますので方程式として処理するか、グラフで処理するか考えさせられることもあります。
ここでは解の位置や文字の範囲をグラフを使った解き方で見ておきましょう。
2次方程式の2つの解がどちらも「正」の場合
\(x\) の2次方程式
\(x^2+2(2k+1)x+(k+1)=0\) が異なる2つの正の解を持つように、
定数 \(k\) の値の範囲を求めよ。
方程式、関数、どちらとしても考察できるようになっておきたいところです。
この問題では解と係数の関係を使いたくなりますが、グラフで考えることも視野に入れておいてください。
解と係数の関係では条件を整えるのにやっかいな場合がありますので、いろいろな問題のケースを考えてグラフ利用が確実です。
解と係数の関係を利用した解き方
方程式として、2解を \(\alpha , \beta\) とすると、
「 \( \alpha>0\) 」かつ「 \(\beta>0\) 」かつ「2解を持つ」が条件です。
\(\color{red}{ \alpha+\beta}=-2(2k+1)>0\\ \\
\Leftrightarrow \displaystyle 2k+1< 0 \Leftrightarrow k< -\frac{1}{2}\)
\( \color{red}{ \alpha\beta}=k+1>0\\ \\
\Leftrightarrow \hspace{10pt} k>-1\)
\( \color{red}{ D/4}=(2k+1)^2-(k+1)>0\\ \\
\Leftrightarrow \hspace{10pt} 4k^2+3k=k(4k+3)>0\\ \\
\Leftrightarrow \hspace{10pt} \displaystyle k < -\frac{3}{4} \hspace{5pt} ,\hspace{5pt} 0 < k\)
を満たせば良いことになります。
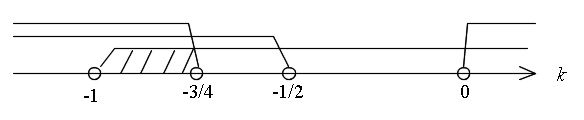
すべてを満たすのは、
\( -1< k < -\displaystyle \frac{3}{4}\)
グラフを利用した解き方
関数として見てみます。
左辺を \(f(x)=x^2-2(2k+1)x+(k+1)\) とすると、
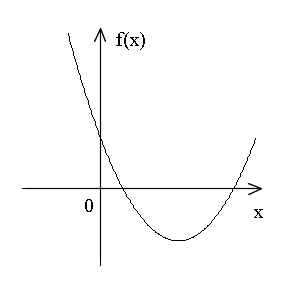
図のようになれば良いので、
・ 軸が正
・ 頂点の \(\color{red}{y}\) 座標は負
・ \(\color{red}{f(0)>0}\)
の3つがそろっていれば条件を満たします。
\( f(x)=x^2+2(2k+1)x+(k+1)\\ \\
=\{x+(2k+1)\}^2-(2k+1)^2+(k+1)\\ \\
=(x+2k+1)^2-(4k^2+3k)\)
と平方完成されるので3つの条件は、
\( \begin{cases}
\hspace{8pt} -(2k+1)>0 \\ \\
-(4k^2+3k)< 0\\ \\
\hspace{20pt} k+1>0
\end{cases}\)
となり、方程式として考えたときと同じ条件になるので、
\( -1< k < -\displaystyle \frac{3}{4}\)
と同じ答えになります。
どちらが良いか?ではなく両方使えるようになってください。
問題によっては、解と係数の関係だけでは厳しいときもあるので、
関数としてグラフを書いて条件を書き出すことは優先して良いかもしれません。
2次方程式の文字の範囲を求める問題の解き方
\(x\) の2次方程式 \(x^2-px+p=0\) が、
-1と1の間に相違なる2つの実数解をもつように、\(p\) の範囲を定めよ。
関数として見れば例題1と同じような問題に見えます。
解と係数の関係で考えるとちょっとややこしいです。
というもの、実際に条件を書き出して見ると、
2つの解を \(\alpha , \beta\) とすると
\(-1< \alpha <1 , -1< \beta< 1 , \alpha \neq\beta \) が条件ですが、
\( -1< \alpha < 1 , -1< \beta < 1\) から
\( -2< \alpha+\beta < 2\) が言えたとしても \( \alpha\beta\) については一筋縄ではいきません。
この説明をすると少し長くなり、理解に苦しむことになる人が出てくると思われるので、関数としてグラフで考えることにしましょう。
(解が2つとも正の場合は解と係数の関係でも割と簡単に進みます。)
左辺を \( f(x)=x^2-px+p\) とおくと、
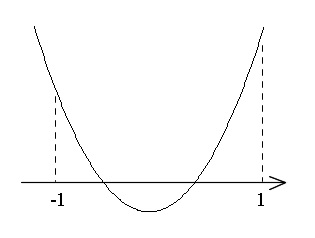
図のようになっていれば良いことになります。
条件で書き出すと、
① 軸が \( \color{red}{-1< x < 1}\) にある。
② \( \color{red}{x}\) 軸との交点が2つある。
③ \(\color{red}{ f(-1)>0 , f(1)>0}\) である。
この条件は図をしっかり見てください。
\( f(x)=\left(x-\displaystyle \frac{p}{2}\right)^2-\displaystyle \frac{p^2}{4}+p\)
より軸は \(\displaystyle x=\frac{p}{2}\) だから①は \(\displaystyle -1< \frac{p}{2} < 1\)
つまり \(-2< p < 2\) ・・・①’
\(f(x)=0\) の判別式が \(D>0\) であれば2つの解を持つので、
\( D=p^2-4p>0\\ \\
\Leftrightarrow \hspace{5pt} p(p-4)>0\)
これを解いて
\( p< 0 , 4< p\) ・・・②’
さらに \( f(-1)=1+2p>0 , f(1)=1>0\) より
\(\displaystyle -\frac{1}{2}< p\) ・・・③’
①’②’③’より、

\( -\displaystyle \frac{1}{2}\,< \,p\, < \,0\)
グラフを使えるようになるとこの手の問題はどれも同じに見えてきますよ。
2次方程式と問題に書いてあっても、
2次関数の問題に自分で置きかえてしまえばグラフで解決できます。