2次方程式や2次不等式の問題はグラフを用いると解き方が簡単になることが多いです。
グラフを持ちなくても解ける問題も多いですが応用問題への対応もできるよう少しでも慣れておくといいでしょう。
絶対値の付いた方程式、不等式の問題への基本も確認しておきます。
絶対値問題の基本は数直線
絶対値を含む問題は、絶対値の中が正か負かで場合分けするのが普通です。
2次関数との融合問題で再確認してみましょう。
グラフを利用すれば2次方程式や不等式が混じっているような応用問題でも、
それほど難しくは感じなくなるので使わない手はありませんよ。
不等式 \( x^2-x-5>|2x-1|\) を解け。
絶対値の方程式、不等式、別の記事でも説明していますがもう慣れた頃でしょうか。
絶対値の中が正か負か(0も含めて)を場合分けすれば良いだけです。
これは方程式も不等式も、1次や2次などの違いはなく同じです。
\( |2x-1|\) の中身で場合分けですね。
左辺の2次式の処理は後で良いのです。
\( 2x-1=0\) を満たすのは \(\displaystyle x=\frac{1}{2}\) なので
これを境界に場合分けをします。
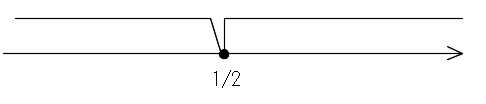
数直線を利用すると分かり易くなるというのは、もう説明は不要でしょう。
ⅰ)
\(\displaystyle x< \frac{1}{2}\) のとき
\( |2x-1|=-(2x-1)\)
となるので
\( x^2-x-5>|2x-1|\\ \\
\Leftrightarrow \hspace{5pt} x^2-x-5>-(2x-1)\\ \\
\Leftrightarrow \hspace{5pt} x^2+x-6>0\\ \\
\Leftrightarrow \hspace{5pt} (x-2)(x+3)>0\\ \\
\Leftrightarrow \hspace{5pt} x< -3 \hspace{5pt}, \hspace{5pt} 2< x \)
\(\displaystyle x< \frac{1}{2}\) のときを考えているから
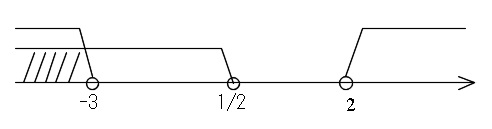
\( x< -3\)
ⅱ)
\(\displaystyle \frac{1}{2}< x\) のとき \( |2x-1|=2x-1\) より
\( s^2-x-5>|2x-1|\\ \\
\Leftrightarrow \hspace{5pt} x^2-x-5>2x-1\\ \\
\Leftrightarrow \hspace{5pt} x^2-3x-4>0\\ \\
\Leftrightarrow \hspace{5pt} (x+1)(x-4)>0\\ \\
\Leftrightarrow \hspace{5pt} x< -1 \hspace{5pt}, \hspace{5pt} 4< x\)
となりますが \(\displaystyle \frac{1}{2}< x\) より
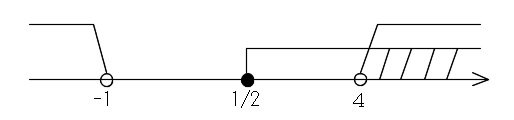
\( 4< x\)
ⅰ)ⅱ)より
\( x< -3 \hspace{5pt} , \hspace{5pt} 4< x\)
ここの「 , 」は「または」の意味になります。
3つ、注意しておいてください。
1つは、\(\displaystyle x=\frac{1}{2}\) は別に場合分けしても良いですが解なしとなるのでⅱ)にまとめました。
2つ目は、ⅰ)およびⅱ)のそれぞれの中では
条件 \(\displaystyle x< \frac{1}{2} , \frac{1}{2}<x\) は「かつ」であること。
3つめは、ⅰ)とⅱ)は場合分けしてあるので、\( x<-3\) と \( 4< x\) は「または」であること。
「かつ」で交わりを見るときと、「または」で結ぶときをしっかり理解してください。
グラフを利用するか判別式を利用するか
\( x\) についての2次不等式
\( x^2-2kx-k+2>0\)
の解が全ての実数となるような \( k\) の範囲を求めよ。
2次不等式の問題なので左辺を2次関数と見ることもできますので、グラフ利用か判別式利用で2つ解法が考えられます。
両方見てみましょう。
1つ目は、左辺を \( y\) とおいて、
\( y=x^2-2kx-k+2\) のグラフを考えます。
\( y=x^2-2kx-k+2\) は下に凸な放物線なので
すべての実数において \( x^2-2kx-k+2>0\) となるには
『 \(y=x^2-2kx-k+2\) の頂点が \( x\) 軸より上にあればいい』
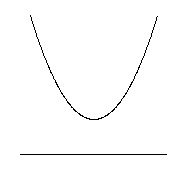
もう一つは、下に凸な放物線なので、\( x\) 軸との交点がなければいい。
つまり、
『 \( x^2-2kx-k+2=0\) の実数解が存在しない』⇔『判別式D<0』
となればいい、ということです。
しかし、この2つは実は同じことです。
実際に処理してみると、2次関数は
\( y=(x-k)^2-k^2-k+2\)
と平方完成されるので頂点は、
\( (k \hspace{5pt},\hspace{5pt} -k^2-k+2)\)
この頂点の \( y\) 座標が0より大きいことが条件だから
\( -k^2-k+2>0 \Leftrightarrow k^2+k-2< 0\) ・・・①
一方、\( x^2-2kx-k+2=0\) の判別式 \( D\) は、
\( D/4=k^2-(-k+2)=k^2+k-2\)
なので
\( D< 0 \Leftrightarrow k^2+k-2< 0\) ・・・②
①と②は全く同じ不等式です。
2次関数が \( x\) 軸との「共有点を持たない」ということと、
2次関数と \( y=0\) との連立において成り立つ2次方程式の「解が存在しない」ということは同じだということです。
\( k^2+k-2< 0\\ \\
\Leftrightarrow (k+2)(k-1)<0\)
\(\Leftrightarrow -2< k < 1\) ・・・(答)
同じ結果なのでどちらを使っても良いということですが、
グラフがどうなれば良いかのイメージ図は書くようにしましょう。
後々の数学への取り組み方が大きく変わりますよ。
絶対値を扱うときの基本は忘れないでくださいね。
