シグマの計算公式が使えない数列の和の計算方法、数式処理のいろいろなパターンをご紹介します。
特別なものではなく、ちょっとした工夫をすれば処理できる程度の問題なので標準的な参考書や問題集でも見かけると思います。
ここまでできるようになれば数式処理は十分です。
さて、今までシグマについて、いろいろと数列の和の問題について書いてきました。
そろそろΣも終わりに近づいてきましたが、今猛烈に反省しています。
もっと練習問題の数を減らしておけば良かった、と。笑
しかし、本当はもっといろいろなパターンをやっておくべきです。
数列は数学Ⅲにつながる重要な単元ですし、規則性を見るということにおいては数学全般で大切ですので、本当に数学らしいといえる重要な単元なんです。
めんどくさいでは済ませられないので続けましょう。
かけて、ずらして、引くと見えてくる数列の和
「 \( S=1+2x+3x^2+\cdots+nx^{n-1}\) を計算せよ。」
これは等差数列でも等比数列でもありません。
係数が等差数列、文字の部分が等比数列、となっていますね。
この形では決まった手法で和を求めます。
等比数列の和の公式を求めるときに使った方法ですが、
公比らしいものを全体にかけて、ずらして引く、
という方法です。良く出てくるので覚えておくと良いです。
\(S=1+2x+3x^2+\cdots+nx^{n-1}\) ・・・①
両辺に \(x\) をかけます。
\( xS= x+2x^2+3x^3+\cdots+(n-1)x^{n-1}+nx^n\) ・・・②
①-②を左辺、右辺それぞれ行いますが、
\( x\) の次数が同じになる項を(全体をずらして)そろえて引く、ということがポイントです。
①②の辺々引くと、
\(\hspace{30pt} S=1+2x+3x^2+4x^3+\cdots+nx^{n-1}\)
\(\underline{-)\hspace{12pt}xS=\hspace{23pt} x+2x^2+3x^3+\cdots+(n-1)x^{n-1}+nx^n}\)
\( (1-x)S=1+\,x\,+\,x^2\,+\,x^3\,+\,\cdots\,+\,x^{n-1}\,-\,n\,x^n\) ・・・③
と少し分かり易い和になりましたが右辺の
\( 1+x+x^2+x^3+\cdots+x^{n-1}\)
部分が初項1,公比が \( x\) の等比数列の和になっているからと、
\( \displaystyle (1-x)S=\frac{1-x^n}{1-x}-nx^n\)
としては絶対ダメです!!!
\(x=1\) のとき分母が0になるので割り算ができません。
分母が0になる可能性があるときは安易に分母に文字を使ってはいけません。
問題に \( x\neq1\) とある場合は問題ありませんが、無い場合は場合分けします。
マーク式試験の場合は問題ありませんが、大学入試本試験で数学が記述式である人は、
この場合分けをきっちり書かないと大減点されるので要注意です。
【Ⅰ】\( x=1\) のとき
\( S=1+2+3+\cdots+n=\displaystyle \frac{1}{2}n(n+1)\)
【Ⅱ】\( x\neq1\) のとき③は、
\( (1-x)S=\displaystyle \frac{1-x^n}{1-x}-nx^n\\ \\
~\hspace{45pt}=\displaystyle \frac{(1-x^n)-(1-x)nx^n}{1-x}\)
両辺を \( x-1\neq 0\) で割って
\(\displaystyle S=\frac{1-(n+1)x^n+nx^{n+1}}{(1-x)^2}\)
\( x-1\neq 0\) だから割れるのです。
ちょっと進んだ話
(ここから先は突っ込んだ話なのでしばらく飛ばしても良いです。)
ここで①-②を計算していますが、何故ずらして引くのかというと、右辺の係数が一定になる部分が出てくるからです。
ここでは引き算した後係数が1になりましたが、係数部分が等差数列で公差が1でないときは、全部の項の係数が公差になりやはり一定となるので、その後等比数列の和の公式が使えるようになるんです。わかりにくいので一般的な例を書き出して見ます。
\(\hspace{22pt} S=a+(a+d)x+(a+2d)x^2+\cdots+\{a+(n-1)d\}x^{n-1}\)
\(\underline{-)\hspace{12pt}xS= \hspace{28pt}ax+\hspace{8pt} (a+d)x^2+\cdots +\hspace{8pt} \{a+(n-2)d\}x^{n-1}+\{a+(n-1)d\}x^n}\)
上の式から下の式を引くと
\( (1-x)S=a+dx+dx^2+\cdots+dx^{n-1}-\{a+(n-1)d\}x^n\) ・・・④
のように部分的に等比数列としてみることができるということです。
「等比数列の部分の初項は?」と思った人は自分で手を動かして計算してみた人ですね。
さすがです。
そうです。④は、\( -d+d\) (=0) を加えるという工夫が必要なんです。
(これはよく使う手法なので覚えておくと良いですね。)
\( (1-x)S=a-d+(d+dx+dx^2+\cdots+dx^{n-1})-\{a+(n-1)d\}x^n\)
この(右辺のカッコ)の中、ここが等比数列の和になっています。
練習23は、初項と公差が等しいので必要無かっただけです。
ちなみに、この問題に限り、商の微分(数学Ⅲ?)を学んだ人は、
\( 1+x+x^2+x^3+\cdots+x^n=\displaystyle \frac{1-x^{n+1}}{1-x} \hspace{10pt}(x\neq1)\)
の両辺を微分してみるとおもしろい結果が出ます。
読み間違いの多い平方の和
「1から始まる連続する \( n\) 個の奇数の平方の和を求めよ。」
これは簡単です。
日本語さえしっかり読めれば今までの知識で十分計算できる問題ですね。
「奇数の平方」の『和』は
\( \displaystyle S=1^2+3^2+\cdots+(2n-1)^2\\ \\
\displaystyle =\sum_{k=1}^n (2k-1)^2\)
です。
『奇数の和』の「平方」
\( \displaystyle S=\{1+3+5+\cdots+(2n-1)\}^2\\ \\
\displaystyle =\left\{\sum_{k=1}^n (2k-1)\right\}^2=n^4\)
ではありません。
\( \displaystyle S=\sum_{k=1}^n (2k-1)^2\)
これ、自分で計算してみて下さい。
決してめんどくさがっているわけではありません。
今までのことが、\(\Sigma\) の計算方法が身についているかのチェックです。
\( S=\displaystyle \frac{1}{3}n(2n-1)(2n+1)\)
となっていれば、合っているはずです。
簡単に数列の一般項が表せないケース
「 \( 1\cdot n+2\cdot (n-1)+3\cdot (n-2)+\cdots+(n-1)\cdot 2+n\cdot 1\) この和を求めよ。」
第 \( k\) 項が表せるか、
Σ計算で \( n\) を定数と見ることができるか、
というややこしい問題ですが、練習25,26を乗り越えればΣ計算の山場は超えたことになります。
おそらくどのようなシグマ(Σ)の形を見ても計算まで進めるようになっています。
まずは第 \( k\) 項を表してみましょう
もう少し多めに書き出して見ますね。
\( 1\cdot n+2\cdot(n-1)+3\cdot(n-2)+4\cdot(n-3)+\cdots+(n-2)\cdot3+(n-1)\cdot2+n\cdot1\)
各項の因数の前部分と後ろ部分を書き出して行くと、
前 \( 1\hspace{7pt},\hspace{14pt}2\hspace{14pt},\cdots,\hspace{7pt}n-1\hspace{7pt},\hspace{7pt}n\)
後 \( n\hspace{7pt},\hspace{7pt}n-1\hspace{7pt},\cdots,\hspace{14pt}2\hspace{14pt},\hspace{7pt}1\)
と、片方は増えて、片方は同じだけ減るときは、「二つの和」を見てみると良いですよ。
二つの因数を足すと、\( \color{red}{1+n で一定}\)なんです。
前の因数を \(a\) ,後ろの因数を \( b\) とすると \( a+b=n+1\) 。
だから、前の因数が
\( \color{red}{a=k}\) なら後ろの因数は \( b=n+1-\color{red}{a}=n+1-\color{red}{k}\)
となっています。
よって、第 \(k\) 項は
\( \color{red}{k}(n+1-\color{red}{k})\)
と表せます。
または、規則性から \(k\) 番目は、
前の因数が \(k\) で、後ろの因数は \( n\) から前の因数より1少ない数を引いている
と気がつけば、\( k\{n-(k-1)\}\) となっていることも分かります。
後はΣの中で \( n\) は定数として処理できればおしまいです。
なれるまでは紛らわしいです。
しかし、この文字の見分けは重要ですよ。
定数か、変数か、これは数学Ⅰからの大きなテーマになっていたはずです。
関数や等式処理を苦手とするか、得意とするか、一つの鍵です。
\( \displaystyle S=\sum_{k=1}^n k(n+1-k)\\ \\
\displaystyle =\sum_{k=1}^n (kn+k-k^2)\\ \\
\displaystyle =\sum_{k=1}^n kn+\sum_{k=1}^n k-\sum_{k=1}^n k^2\\ \\
\displaystyle =n\sum_{k=1}^n k+\sum_{k=1}^n k-\sum_{k=1}^n k^2\\ \\
\displaystyle =(n+1)\sum_{k=1}^n k-\sum_{k=1}^n k^2\)
\(n\) は定数だからΣの前に出す、ということはもう説明は必要ありませんね。
上の解法のように確実に展開しても良いし、
\( (kn+k-k^2)=(n+1)k-k^2\)
と整理してからΣ計算に入っても良いです。
\( \displaystyle S=\sum_{k=1}^n k(n+1-k)\\ \\
\displaystyle =\sum_{k=1}^n \{(n+1)k-k^2\}\\ \\
\displaystyle =(n+1)\sum_{k=1}^n k-\sum_{k=1}^n k^2\\ \\
\displaystyle =(n+1)\frac{1}{2}n(n+1)-\frac{1}{6}n(n+1)(2n+1)\\ \\
\displaystyle =\frac{1}{6}n(n+1)\{3(n+1)-(2n+1)\}\\ \\
\displaystyle =\frac{1}{6}n(n+1)(n+2)\)
ところで、
「かっこいい解法はないか?」と考えて、
問題の和が左右対称(左から \(k\) 番目と右から \( k\) 番目が同じ)だからと策を練ると、
項数が奇数か偶数かで場合分けが待っていて、あんまりかっこよくはありません。
、、、でした。
「1・3,2・4,3・5,・・・の第 \( n\) 項までの和を求めよ。」
これは第 \( k\) 項が表せれば後は簡単なΣ計算だけです。
\(1\cdot 3 , 2\cdot4 , 3\cdot5 , 4\cdot 6 ,\cdots\) ・・・⑤
数列でよくこのような(二つの数の積が一つの項になっている)形で問題が出ます。
これが、
\(3 , 8 , 15 , 24 ,\cdots\) ・・・⑥
となっていたら急にややこしくなりますね。
⑥の形で問題が出たら、「因数ごとに注目しなさい。」とヒントをくれているのです。
前の因数は、\(1,2,3,\cdots\) となっていて \( k\) 番目は \( k\)
後の因数は、\(3,4,5,\cdots\) となっていて \( k\) 番目は \( k+2\) です。
だから \(k\) 番目(全体)は \( k(k+2)\) となって、 ・・・☆
\( \displaystyle S=\sum_{k=1}^n k(k+2)\\ \\
\displaystyle =\sum_{k=1}^n (k^2+2k)\\ \\
\displaystyle =\sum_{k=1}^n k^2+2\sum_{k=1}^n k\\ \\
\displaystyle =\cdots\\ \\
\displaystyle =\cdots\\ \\
\displaystyle =\frac{1}{6}n(n+1)(2n+7)\)
途中計算は自分でやって見てください。
記述するのがめんどくさいのではなく、ここまできたらできるはずなのでやって見てください。
人の計算見て、自分ができている気になっているからいつまでも数学の成績良くならない、計算力付かない、って人多いですからね。
⑥の形ででたら、『階差』をとるのが普通です。(これはここでは説明しません。)
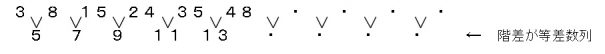
さらに、この一般項の和をとります。
すると結局・・・☆に戻ることになります。
「 \( 11^3\,,\,12^3\,,\,13^3\,,\,14^3\,,\cdots\) の第 \(n\) 項までの和を求めよ。」
一つひとつは3乗の数なのでΣの計算公式が使えますが、始まりが \(1^3\) ではありません。
\( k\) 番目が \( k^3\) のときの第1項から \( n\) 項までの和に
\( \displaystyle \sum_{k=1}^n k^3=\left\{\frac{1}{2}n(n+1)\right\}^2\)
が使えるのです。
使い方のところで示した方法2つともやってみましょう。
第 \(k\) 項を \((k+10)^3\) とすると、
\( \displaystyle S=\sum_{k=1}^n (k+10)^3\\ \\
\displaystyle =\sum_{k=1}^n (k^3+30k^2+300k+1000)\\ \\
\displaystyle =\sum_{k=1}^n k^3+30\sum_{k=1}^n k^2+300\sum_{k=1}^n k+1000\sum_{k=1}^n 1)\)
ここまでして始めて基本の計算公式が使えますね。
また、
\( S=11^2+12^2+13^2+\cdots+(n+10)^2\)
何度もいってきたつもりですが、(いってませんか?)この書き出しは基本です。
\(\color{red}{\sum は『和』}\)です。
Σで問題に与えられても、記号のまま眺めるのではなく先ずは具体的に考える、数学の基本です。
いや、数学やその上に乗っている科学すべての基本と言えるのではないでしょうか。
続けます。
\( S=(1^2+2^2+\cdots+10^2)+11^2+12^2+\cdots+(n+10)^2-(1^2+2^2+\cdots+10^2)\)
と(カッコ)部分を足して、引けば全体の和は変わらないので、
\( \displaystyle \sum_{k=1}^n k^3=\{\frac{1}{2}n(n+1)\}^2\)
が使えるようになります。
\( \displaystyle S=\sum_{k=1}^n (k+10)^3\\ \\
\displaystyle =(1^2+2^2+\cdots+10^2)+11^2+12^2+\cdots+(n+10)^2-(1^2+2^2+\cdots+10^2)\\ \\
\displaystyle =\sum_{k=1}^{n+10} k^3-\sum_{k=1}^{10} k^3\\ \\
\displaystyle =\frac{1}{4}(n+10)^2\{(n+10)+1\}^2-\frac{1}{4}(10)^2\{(10)+1\}^2\)
のように変形すれば計算公式を使えますが、今までの練習で使えるようになっていますか?
(メンドクサイのではありませんよ。念のため。)
\( \displaystyle S=\frac{1}{4}n(n^3+42n^2+661n+4620)\)
となります。
いかがでしょう?
ここまでやってきてΣの意味と使い方、計算方法はだいたい分かってきましたか?
後はΣの中身、つまり「 \( k\) の関係式」のパターン練習だけです。
いくつかあげておきますので見ておいて下さい。
良いですか?
\(\color{red}{\sum は『和』}\)です。
どれだけ具体的に書き出せるか、それが解法の糸口です。
次で最終章となります。
いったん休憩して下さい。
ここがまったくわからないという人は
は復習しておくといいでしょう。
次はシグマの計算練習としては一応のラスト
良く出る覚えておくべき方法(パターン)です。
