データの分析問題で差がつくのは分散や標準偏差を求める部分です。
また相関係数は共分散と散布図が関連して聞かれます。
これらの問題は考えれば答えが出るのではなく、知らなければ答えが出ない問題になるので算出する公式は覚えておきましょう。
箱ひげ図と平均値の出し方確認
データの分析問題で聞かれることはそれほど多くありません。
代表値、箱ひげ図、分散、標準編差、相関係数、散布図などですが、知っていないと答えられない用語と公式があります。
そのうち箱ひげ図の書き方と平均値までは先に説明しておきました。
⇒ データの分析の問題と公式:箱ひげ図の書き方と仮平均の使い方
今回はその続きです。
問題のデータは同じですが、問題に相関係数を求める問題を加えておきました。
次の問いに答えよ。
ある高校の1年生の女子8人の記録が下の表にある。
| 生徒 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 50m走(秒) | 8.5 | 9.0 | 8.3 | 9.2 | 8.3 | 8.6 | 8.2 | 9.5 |
| 1500m走(秒) | 306 | 342 | 315 | 353 | 308 | 348 | 304 | 324 |
(1)50m走の記録の箱ひげ図を書け。
(2)50m走と1500m走の記録の分散および標準偏差を求めよ。
(3)2つの記録の相関係数を小数第2位まで求めよ。
(1)の箱ひげ図は書けるようになっていると思います。
(2)から始めますが、
分散を出すには平均値が必要です。
ただしこちらもすでに算出済みなので、結果を利用します。
50m走の平均値は 8.7 1500m走の平均値は 325 でした。
(単位はどちらも「秒」です。)
これを利用して分散を出しに行きます。
分散と標準偏差を求める公式
その前に、分散とは何か?思い出しておきましょう。
変量 \(x\) と平均値 \(\bar{x}\) との差を偏差といいます。
偏差: \(\color{red}{x-\bar{x}}\)
あるデータにおいてこの偏差を全て足すと、0 になります。(偏差の総和が0)
具体例をあげると、50m走のデータから平均値は 8.7 でした。
偏差の合計は、8つのデータ、
\( 8.5\,,\, 9.0\,,\, 8.3\,,\, 9.2\,,\, 8.3\,,\, 8.6\,,\, 8.2\)
から
\( (8.5-8.7)+(9.0-8.7)+(8.3-8.7)+(9.2-8.7)\\ \\
+(8.3-8.7)+(8.6-8.7)+(8.2-8.7)+(9.5-8.7)=0\)
一般的に書くと、
\( (x_1-\bar x)+(x_2-\bar x)+\cdots+(x_n-\bar x)\\ \\
=(x_1+x_2+\cdots +x_n)-n\cdot \bar x\\ \\
=(x_1+x_2+\cdots +x_n)-n\cdot \underline{\displaystyle \frac{1}{n}(x_1+x_2+\cdots +x_n)}\\ \\
=(x_1+x_2+\cdots +x_n)-(x_1+x_2+\cdots +x_n)\\ \\
=0\)
となるので、偏差の総和ではデータの散らばり具合が表せません。
※
\( \underline{\frac{1}{n}(x_1+x_2+\cdots +x_n)}\) が平均 \( \bar x\) です。
そこで登場するのが、分散です。
分散:ある変量の、偏差の2乗の平均値
つまり、50m走の記録の分散は
\( \{(8.5-8.7)^2+(9.0-8.7)^2+(8.3-8.7)^2+(9.2-8.7)^2\\
+(8.3-8.7)^2+(8.6-8.7)^2+(8.2-8.7)^2+(9.5-8.7)^2\}\color{red}{\div 8}\)
この{偏差の2乗の総和}、をデータ数8で割ったものです。
一般的に書くと、変量 \(x\) のデータが \(n\) 個あるときの分散 \(s^2\) は、
平均値を \(\bar x\) とすると、
\(\displaystyle s^2=\frac{1}{n}\{(x_1-\bar x)^2+(x_2-\bar x)^2+\cdots +(x_n-\bar x)^2\}\) ・・・①
ですが、展開して整理すると、次の公式が成り立ちます。
\( s^2=\overline{x^2}-(\bar x)^2\) ・・・②
(データをそれぞれ2乗したものの平均)-(平均の2乗)
で2つの表している数値の意味が違いますから注意してください。
どちらかというとプログラムを使わず手で計算する場合は、②の計算の方が便利な場合が多いです。
入試では計算ソフトはおろか電卓も使えません。
手計算になるので②を優先して使った方が得策だと思えますが、問題によっては①でもまったく構いませんよ。
そして、分散 \( s^2\) の「正の平方根 \( s\) 」 が標準偏差です。
\(\displaystyle s=\sqrt{\frac{1}{n}\{(x_1-\bar x)^2+(x_2-\bar x)^2+\cdots +(x_n-\bar x)^2\}}\) ・・・③
①②同様に、③も、次の公式が成り立ちます。
\( s=\sqrt{\overline{x^2}-(\bar x)^2}\) ・・・④
覚えることが多いように思えますが、実際は少ないですし、
覚えておかなければ使えませんので必ず覚えておくようにしましょう。
この計算は通常計算ソフトがやってくれます。
紙面で計算をやらなければならない試験では、もっと簡単な数値で出題されます。だから練習問題の数値を簡単なものを選んで使いこなせる練習をした方が良いのです。
もし、数値が大きい計算が出題されたとしても、使い方がわからなければ意味はないのですよ。
問題の(2)分散と標準偏差を求めましょう。
「ややこしそうに見える」表を作成します。
書き出すとほとんどが計算しているものなのですが、
まとめてみるとややこしく見えるのです。
\( x=8.7 , y=325\) と出してあるので、共分散まで出せるように、
| 生徒 | \( x\) | \( y\) | \( x-\bar x\) | \( y-\bar y\) | \( (x-\bar x)^2\) | \( (y-\bar y)^2\) | \( (x-\bar x)(y-\bar y)\) |
| 1 | 8.5 | 306 | -0.2 | -19 | 0.04 | 361 | 3.8 |
| 2 | 9.0 | 342 | 0.3 | 17 | 0.09 | 289 | 5.1 |
| 3 | 8.3 | 315 | -0.4 | -10 | 0.16 | 100 | 4.0 |
| 4 | 9.2 | 353 | 0.5 | 28 | 0.25 | 784 | 14.0 |
| 5 | 8.3 | 308 | -0.4 | -17 | 0.16 | 289 | 6.8 |
| 6 | 8.6 | 348 | -0.1 | 23 | 0.01 | 529 | -2.3 |
| 7 | 8.2 | 304 | -0.5 | -21 | 0.25 | 441 | 10.5 |
| 8 | 9.5 | 324 | 0.8 | -1 | 0.64 | 1 | -0.8 |
| 計 | 69.6 | 2600 | 0 | 0 | 1.60 | 2794 | 41.1 |
と、ここまでの表ができれば後は計算のみです。
つまり、「ややこしいと見える」この表さえ作れれば、分散、標準偏差は出せると言うことです。
何故、共分散まで出せる、と言わないかというと、多くの問題に電卓がいる計算が待っているからなんです。
(共分散の計算公式は後で説明します。)
ここでも電卓があればはやいのですが、
(表計算ソフトがあればもっとはやい)
自力で計算できるようにしてみますので、自分でもやってみて下さい。
まずは偏差の和が0になっているのを確認しましょう。
次に、分散ですが、①の
\( s^2=\displaystyle \frac{1}{n}\{(x_1-\bar x)^2+(x_2-\bar x)^2+\cdots +(x_n-\bar x)^2\}\)
と表の値から、
50m走の分散は \( 1.6\div 8=0.2\)
1500m走の分散は \( 2794\div 8=349.25\)
となるのですが、標準偏差まで出そうとするとき小数は計算がやっかいです。
答えにはなりませんが、計算過程の段階として、
50m走の標準偏差は
\( s_x=\sqrt{\displaystyle \frac{1.6}{8}}=\sqrt{\displaystyle \frac{1}{5}}\)
1500m走の標準偏差は
\( s_y=\sqrt{\displaystyle \frac{2794}{8}}=\sqrt{\displaystyle \frac{1397}{4}}\)
と、とどめておくのも1つの手です。
マーク式の問題では平方根がおおよそ推定できるか、計算が楽な問題となると思いますが、
この \( \sqrt{a}\)(根号付き)のまま答えを埋める問題も出てきます。
いずれにしても途中の計算が必要になるかもしれないので、問題用紙の片隅でどこに書いたか分からないような計算ではなく、計算過程も確認出来るようにまとまりを持たせておきましょう。
これはマーク式の場合の解答上大切なことです。
分散は「偏差の2乗の和の平均」であり、標準偏差はその「正の平方根」であるというのは良いですね。
(ここは繰り返し見ておいて下さい。)
標準偏差を小数にすると共分散の有効数字があやふやになる人が多いので、上の値を標準偏差としておきます。
ちなみに、
50m走の標準偏差は \( 0.4472 \cdots\)
1500m走の標準偏差は \( 18.688 \cdots\)
です。
共分散と相関係数を求める公式と散布図
(3)相関係数とは、2つのデータの関係性を示す値の1つです。
例えば、
数学のテストの点数が高い人は、物理のテストの点数も高い、という傾向がはっきりと見て取れる場合、正の相関があるといいます。
このとき相関係数 \(r\) は、+1に近い値となります。
また、逆の傾向が見られるとき、
例えばスマホを触っている時間が長い人は、数学のテストの得点が低い、などのあることが大きくなると他方が小さくなるといった場合、負の相関があるといい、-1に近い値となります。
相関係数が0に近いときは「相関がない」または「相関関係はない」と言います。
いずれにしても、相関係数は \( \color{red}{-1≦ r ≦ 1}\) にあることは記憶しておきましょう。
ただし、一般的には相関係数の絶対値が 0.6 以上の場合、割と強い相関を示すといわれますが一概には言えません。
データ数が少ない場合や、特別な集団でのデータはあてにはなりません。
データは、無作為かつ多量なデータにより信頼性を持たせる必要があるのです。
さて、相関係数 \(r\) を求める方法を示します。
データ \(x\) と \(y\) における標準偏差を \(s_x , s_y\) とし、共分散を \(c_{xy}\) とすると、
相関係数 \(r\) は
\(\displaystyle r=\frac{c_{xy}}{s_x\cdot s_y}\) ・・・⑤
共分散とは、上の表で見ると一番右の平均 \(41.1\div 8\) のことです。
公式と言うより定義ですが、共分散を式で示すと、
\( c_{xy}=\displaystyle \frac{1}{n}\{(x_1-\bar x)(y_1-\bar y)+(x_2-\bar x)(y_2-\bar y)+\cdots +(x_n-\bar x)(y_n-\bar y)\}\)
(データ \(x\) と \(y\) の偏差をかけて、和したものの平均)
計算しても良いですが、求めたいのは相関係数なので計算は後回しとする方が楽になることが多いです。
\( r=\displaystyle \frac{c_{xy}}{s_x\cdot s_y}\\ \\
=\displaystyle \frac{\displaystyle \frac{41.1}{8}}{\sqrt{\displaystyle \frac{1.60}{8}}\cdot \sqrt{\displaystyle \frac{2794}{8}}}\\ \\
=\displaystyle \frac{41.1}{\sqrt{1.60}\cdot \sqrt{2794}}\\ \\
=0.614\cdots ≒ 0.61\)
これ、どう見ても電卓必要な気がしますよね。
(小数第一位までは簡単に出せますが)
もちろん、丁寧に根号を外せば出せない数字ではありませんが、このケースだと相関係数は問題に書き込まれ、どのような相関があるかを聞かれると思います。
そして、相関関係については「正の相関がある」となりますが散布図は図のようになり、
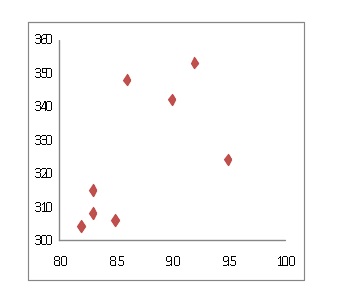
相関があるとは思えないような気がしません?
データが少なくどういう傾向かもわかりませんね。
50m走が速ければ、1500m走も速いのか?
断言はできないし、わからない。
このデータを信頼するのか、しないのか、条件が必要なのです。
だから突っ込んで行くと、ⅡBの統計になるので、それほど深くする必要はあまりないということですね。
覚えておかなければならないのは、
箱ひげ図、分散、標準偏差、共分散、相関係数(散布図)
などの基本的な用語と求め方(定義や公式)です。
⇒ データの分析の問題と公式:箱ひげ図の書き方と仮平均の使い方
箱ひげ図からもう一度やり直しておくと確実に点が取れる分野ですよ。
平成28年度、29年度と続いた傾向の問題を中学生でも解く方法
中学生でも解ける方法もあります。
この単元、試験の1日前には必ず復習しておくことをお勧めします。
