データの分析では問題を解くとき用語や公式を覚えていないと全く通用しません。
考えればわかる問題ではなく、基本用語の確認問題がほとんどだからです。
問題を通してもう一度基本用語と公式を確認しておきましょう。
先ずは箱ひげ図の書き方と仮平均の使い方です。
問題は1つだけです。
2ページにわたっての説明になりますが、データの分析で出てくる用語のほとんどをおさらいできるようにします。
データの分析問題に取り組みにくいのは何故か?
問題を見てみましょう。
次の問いに答えよ。
ある高校の1年生の女子8人の記録が下の表にある。
| 生徒 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 50m走(秒) | 8.5 | 9.0 | 8.3 | 9.2 | 8.3 | 8.6 | 8.2 | 9.5 |
| 1500m走(秒) | 306 | 342 | 315 | 353 | 308 | 348 | 304 | 324 |
(1)50m走の記録の箱ひげ図を書け。
(2)50m走と1500m走の記録の分散および標準偏差を求めよ。
「データの分析」は、中学1年生の「資料の整理」からの延長です。
長くなるのでここでは資料の整理で出てきた用語はパスしますので、まずは中学の資料の整理をもう一度やり直しておいて下さい。
この問題はまだやりやすいですが、データの分析問題はとにかく長い、文字数多い、データの表がたくさん、と情報が入り過ぎっていうくらい入っています。
公式を覚えていないと話にならない分野ですが、このデータの読み取りに時間がかかるのでとり組みにくくなっているのです。
読み取りできれば覚えている公式を使って解けるので難しいことはありません。
センターでも、問題慣れしていないと得点しにくくなってきています。
これは共通テストになっても変わりません。
基本用語の確認
ここで出てきている用語は必ず覚えておくようにしましょう。
箱ひげ図
「箱ひげ図」はデータの散らばり具合を度数について区切った「箱とひげ」でできた図です。
ここで注意して欲しいのはデータの値が区切りになるのではなく、
(幅の大きさはデータの値の範囲です。)
データの度数(人数など)で区切るので度数による区分分けとなっていることです。
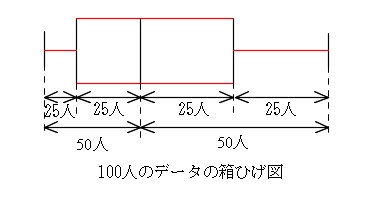
箱ひげ図の書き方手順
(1)箱ひげ図を書くために必要なのは、「四分位数」ですね。
箱ひげ図の書き方を今から順を追って説明しますので難しく考えなくていいです。
先ずデータを小さい順に並べます。
8.2 8.3 8.3 8.5 8.6 9.0 9.2 9.5
これから最小値は8.2、最大値は9.5 となるので、範囲が決まります。
手順①
(ひげの両端が書けます。)

このデータの中央値は、4番目と5番目の平均になるので、
\( (8.5+8.6) \div 2=8.55\)

これが第2四分位数 \(Q_2=8.55\) (中央値)です。
手順②
この中央値の、左の4つのデータの中央値が、
第1四分位数 \(Q_1=(8.3+8.3)\div 2=8.3\) です。
手順③
反対の中央値の、右側4つのデータの中央値が、
第3四分位数 \(Q_3=(9.0+9.2)\div 2=9.1\) です。
手順④
もう一度、データを並べて書き込むと、

となります。
これを箱ひげ図にすると、(おおよそのスケールで書くと)
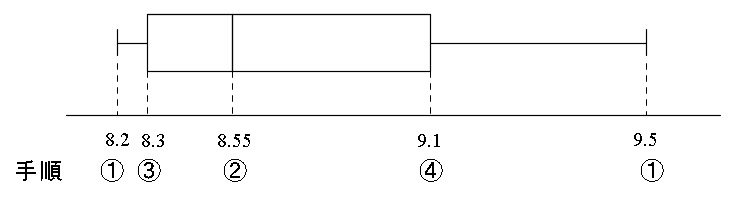
となります。
箱ひげ図の書き方手順の確認
もう一度手順を追うと、
・ 最小、最大を書き込む。
・ 次に中央値 \(\color{red}{Q_2}\) および \(\color{red}{Q_1\,,\,Q_3}\) を書き込み、\(\color{red}{Q_2\,,\,Q_1\,,\,Q_3}\) で長方形を2つ書く。
・ 後は「ひげ」をつければおしまいです。
\(Q_3-Q_1\) を「四分位範囲」といいますが、
これを長方形にして中央値で分割するだけですね。
箱ひげ図はデータの散らばりを視覚的にとらえられるので、
最小値を基準に、おおよそでいいので(定規が使えないので)最大値までの間隔を,
見た目でしっかりわかるように書くと良いですよ。
(簡単に見ると、中央値 \(Q_2\) の左右に同じ人数いる。)
箱ひげ図に、平均値を「+」として書き込むことがありますが、なくても良いです。
もし、箱ひげ図に「+」があれば「平均値」だとわかっていればそれでいいです。
もう一度値なしで箱ひげ図の書き方を見ると、
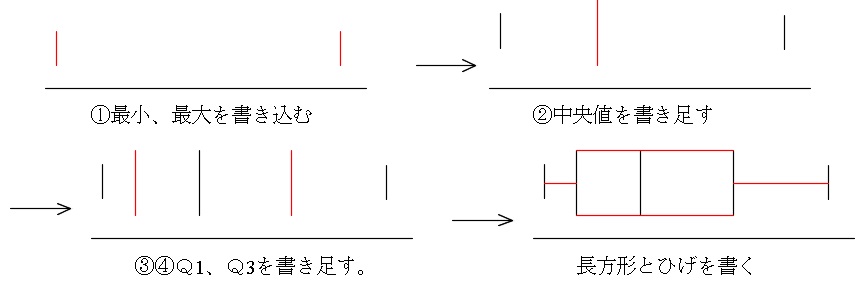
平均値の求め方と仮平均の利用
(2)分散ですが、まずは平均値が必要です。
平均値は中学1年生でやってますので必要無いと思いますがもう一度見ておきましょう。
平均値は全てのデータを足して、度数合計の8で割れば出てきます。
中学生にはこちらを勧めています。
データ自体が少ない問題が多いから、実際の数値を見ながら平均を出し、
平均からのズレ(散らばり)を実感してもらうということです。
しかし、実際に計算するとデータが大きい場合、計算がやっかいな場合が多いです。
時間もかかります。
そこで、ここでは「仮平均」を使った平均値の出し方でやっておきます。
ただ、度数分布表から仮平均を利用した算出方法はあつかいません。
センター試験を目的にしているので、基本的なことにとどめておきます。
仮平均は、中央値(メジアン)の前後の値を使う、または最頻値(モード)を使うと小さい数値で計算が進みますので便利です。
(1)で中央値を出していますので、今は中央値を使います。
50m走の中央値は8.55だったので仮平均を8.6としておきましょうか。8.5でも良いです。
(何故、8.55のまま仮平均をおかないかというと、変量を0にするところをつくり計算を有利に進めるためです。)
50m走の記録を \(x\)(秒),50m走の仮平均を8.6とすると
見やすくするため表にします。
| 生徒 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 計 |
| \( x\) | 8.5 | 9.0 | 8.3 | 9.2 | 8.3 | 8.6 | 8.2 | 9.5 | 69.6 |
| \( x-8.6\) | -0.1 | 0.4 | -0.3 | 0.6 | -0.3 | 0.0 | -0.4 | 0.9 | 0.8 |
仮平均からの「ズレの平均」が
\(\overline{x-8.6}\\ \\
=(-0.1+0.4-0.3+0.6-0.3+0-0.4+0.9)\div 8\\ \\
=0.8\div 8=0.1\)
となるので、これを仮平均に加え、
\( x\) の平均値は \( \bar x=8.6+01=\underline{8.7}\)
が50m走の記録の平均値となります。
これは実際に \( x\) から計算した 8.7 と当然一致します。
\( (69.6\div 8=8.7)\)
変量 \( x\) ,仮平均を \( x_0\) とすると、仮平均との差を \( u\) と変換し、
\( u=x-x_0\) から \( x=u+x_0\) となり \( \bar x=\bar u+x_0\)
となっているのですが、式の理解に苦しむし、実際には表にした方がはやいです。笑
同様に、1500m走の記録をy(秒)1500m走の仮平均を320 とすれば、
(中央値が 319.5 であることから仮平均を 320 にしてみました。)
| 生徒 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 計 |
| \( y\) | 306 | 342 | 315 | 353 | 308 | 348 | 340 | 324 | 2600 |
| \( y-320\) | -14 | 22 | -5 | 33 | -12 | 28 | -16 | 4 | 40 |
\( \overline{y-320}\\ \\
=(-14+22-5+33-12+28-16+4)\div 8\\ \\
= 40\div 8=5\)
よって1500m走の平均値は、
\(\bar y=320+5=\underline{325}\)
もちろんこれも \(y\) から直接計算した、2600÷8=325 に一致します。
仮平均を利用すれば計算が楽になると言うだけですが、
実際のセンターではこの程度の計算まではさせると思いますので、
「仮平均」の使い方、覚えておいた方がはやいですよ。
さて、平均値が出たら後は、偏差、分散、標準偏差を出すための表作りです。
この表が分散、標準偏差、共分散、相関係数を出すときに非常に役に立ちます。
次は分散、標準偏差および相関係数です。
⇒ データの分析問題(分散、標準偏差と共分散、相関係数を求める公式)
ここから差が出ます。
少しでも高得点をとりたいなら、必ずと言って良いほど聞かれる項目なのでおさえておきましょう。