空間座標の垂線ベクトルと直線と平面の方程式

空間座標では直線の方程式と平面の方程式もありますので簡単にですが紹介しておきます。
空間ベクトル、特に空間座標は位置関係が書き出しにくく、わかりにくいです。
しかし、平面に垂直なベクトル（法線ベクトル）やその長さの問題は良く出されるので捨ててはおけません。

空間図形、空間座標での図と定理の利用法

まず例題を見てみましょう。

例題

　原点\(\,\mathrm{O}\,\)および点　\( (\,1,2,-1\,)\)　を通る直線を　\( \ell\)　とし、
　点\(\,\mathrm{A}\,\)\((\,0,1,1\,)\)　から直線　\( \ell\)　に下ろした垂線の足を\(\,\mathrm{B}\,\)とするとき、
　ベクトル　\(\overrightarrow{\mathrm{OB}}\)　を求めよ。

位置関係がすぐにイメージできますか？
空間図形、特に座標系で空間の位置関係を正確に書き出すというのは困難で、書けば書くほど分からなくなってくることが多いです。

空間図形では、ある程度書き出したら、平面を抜き出すということで、対処できます。
しかし、座標系となると「やめておいた方がいい」といいたくなります。
余程慣れていないと無駄な時間をとられるだけです。

では、どうすればいいか？
ある程度の位置関係がつかめる図示ができたら、「関係式に頼る」方が良いでしょう。

関係式とは、垂直条件や長さの関係式です。

教科書では空間の直線の方程式や平面の方程式があまり詳しく取り上げられていません。
だから、少ない条件を駆使する必要がありますが、定理は平面とさほど変わりありません。

2つの空間座標の軸の書き方

具体的に見るために例題を座標系で図示してみます。
軸の取り方は空間では２種類あります。

どちらも直交座標系の話ですが、

のように\(\,x\,\)軸の正の方向に対し反時計回りに\( \,y\,\)軸　→　上に\( \,z\,\)軸ととるのは同じですが見る方向が違います。

（この軸の取り方は「右手系」と呼ばれます。)
どちらが良いと言うことはありません。
そのときそのときで見やすい方を使えばいいですよ。

例えば、「原点\(\,\mathrm{O}\,\)および点\( (\,1,2,-1\,)\)を通る直線を\( \,\ell\,\) 」を図示すると、
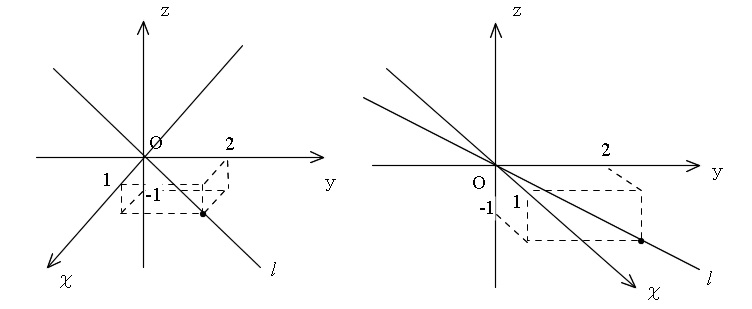のような感じになりますが、この場合それほど変わりませんよね。

座標軸がない方が分かりやすいです。
もう一度問題を見てみます。

　「原点\(\,\mathrm{O}\,\)および点\( (\,1,2,-1\,)\)を通る直線を\(\, \ell\,\)とし、
　点\(\,\mathrm{A}\,\)\((\,0,1,1\,)\)から直線\(\,\ell\,\)に下ろした垂線の足を\(\,\mathrm{B}\,\)とするとき、
　ベクトル\(\,\overrightarrow{\mathrm{OB}}\,\)を求めよ。」

直線　\( \ell\)　は原点を通る直線で、
直線上の点である垂線の足は\( \overrightarrow{\mathrm{OB}}=(\,k\,,\,2k\,,\,-k\,)\)とおけます。

点\(\,\mathrm{A}\,\)が直線上にないことはすぐに分かるので、位置関係をおおまかに図示すると、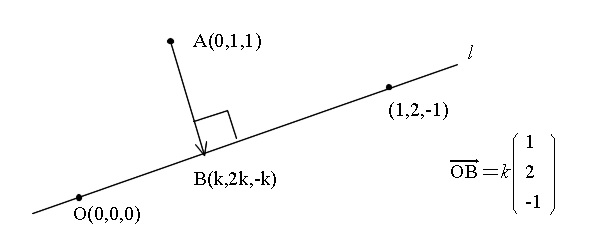となります。
（自分でイメージを書いてみるとわかりやくなりますよ。）

この位置関係は、\( \overrightarrow{\mathrm{OB}}\)　または方向が同じベクトル　\( (1,2,-1)\)　と、
　\( \overrightarrow{\mathrm{AB}}\)　が直交する、つまり「内積が\(\,0\,\)」であれば良いということになります。

　\(\begin{eqnarray}
\overrightarrow{\mathrm{AB}}&=&\overrightarrow{\mathrm{OB}}-\overrightarrow{\mathrm{OA}}\\
&=&(k,2k-1,-k-1)
\end{eqnarray}\)

と\( \,(\,1,2,-1\,)\,\)の内積をとると

　\( k\times 1+(2k-1)\times 2+(-k-1)\times (-1)=0\)

から　\(\displaystyle k=\frac{1}{6}\)

よって

　\(\begin{eqnarray}
\overrightarrow{\mathrm{OB}}&=&\left(\displaystyle \frac{1}{6}\,,\,\displaystyle \frac{2}{6}\,,\,-\displaystyle \frac{1}{6}\right)\\
&=&\left(\displaystyle \frac{1}{6}\,,\,\displaystyle \frac{1}{3}\,,\,-\displaystyle \frac{1}{6}\right)
\end{eqnarray}\)

位置関係さえつかめば内積で答えが出せますね。

図示するのは非常に大切なことですが、
空間座標上では逆にわかりにくくなることもあるので、
　「位置関係をつかむ」⇒「ベクトルの性質利用」
を意識しておきましょう。

空間座標での直線の方程式

空間座標系における直線の方程式は、
方向ベクトルを　\( (a,b,c)\)　とし、点　\( (x_0,y_0,z_0)\)　を通る直線は、

　\(\large{\color{red}{\displaystyle \frac{x-x_0}{a}=\frac{y-y_0}{b}=\frac{z-z_0}{c}}}\)

と表せます。
これはベクトル方程式に成分を与え、媒介変数を消去しただけの定理ですので使ってかまいません。

この問題に置き換えると、方向ベクトルは　\( (1,2,-1)\)　通る点は原点　\( (0,0,0)\)　か　\( (1,2,-1)\)

原点を通る方は上で示しましたので　\( (1,2,-1)\)　を通るとすると、
\( t\)　を媒介変数（パラメータ）として
　\(\hspace{10pt} \displaystyle \frac{x-1}{1}=\displaystyle \frac{y-2}{2}=\displaystyle \frac{z+1}{-1}=t\)
から
　\(\hspace{10pt} (x\,,\,y\,,\,z)=(t+1\,,\,2t+2\,,\,-t-1)\)　とおけるので、　･･･①

　\(\overrightarrow{\mathrm{OB}}=(t+1\,,\,2t+2\,,\,-t-1)\)
としても問題はなく、
　\(\hspace{10pt} \overrightarrow{\mathrm{AB}}=\overrightarrow{\mathrm{OB}}-\overrightarrow{\mathrm{OA}}\\ \\
=(t+1\,,\,2t+2\,,\,-t-1)-(0\,,\,1\,,\,1)\\ \\
=(t+1\,,\,2t+1\,,\,-t-2)\)
とベクトル　\( (1,2,-1)\)　の内積が０が条件となり、
　\(\displaystyle t=-\frac{5}{6}\)
から
　\(\hspace{10pt} \overrightarrow{\mathrm{OB}}=\left(\displaystyle \frac{1}{6}\,,\, \displaystyle \frac{1}{3}\,,\, -\displaystyle \frac{1}{6}\right)\)

と同じ結果になります。

①の媒介変数表示から上の定理が出てくるのですが、どちらが先でも気にしなくて良いです。
使えるようになることが先！

直線の方程式を利用する際、「原点を通る」とするとどうなるか見ておきます。

　方向ベクトル　\( (1,2,-1)\)　通る点は原点　\( (0,0,0)\)

とすると直線の方程式は

　\(\hspace{10pt} \displaystyle \frac{x}{1}=\displaystyle \frac{y}{2}=\displaystyle \frac{z}{-1}=t\)
　
となるので　\( \overrightarrow{\mathrm{OB}}=(\,t\,,\,2t\,,\,-t\,)\)

　\(\hspace{10pt} \overrightarrow{\mathrm{AB}}=\overrightarrow{\mathrm{OB}}-\overrightarrow{\mathrm{OA}}\\ \\
=(\,t\,,\,2t\,,\,-t\,)-(\,0\,,\,1\,,\,1\,)\\ \\
=(\,t\,,\,2t-1\,,\,-t-1\,)\)

このベクトルと　\( (\,1,2,-1\,)\)　との内積が０となるので、
媒介変数の文字\(\,t\,,\,k\,\)が変わっただけで、上で示した答えと同じになります。

空間座標における平面の方程式

空間の平面の方程式もあります。
　点\(\, (\,x_1\,,\,y_1\,,\,z_1\,)\,\)を通り、ベクトル\(\, \vec{n}=(\,a\,,\,b\,,\,c\,)\,\)に垂直な平面は

　\(\hspace{10pt} \large{\color{red}{a(x-x_1)+b(y-y_1)+c(z-z_1)=0}}\\ \\
\Leftrightarrow \\ \\
　 \large{\color{red}{ax+by+cz+d=0}}\)

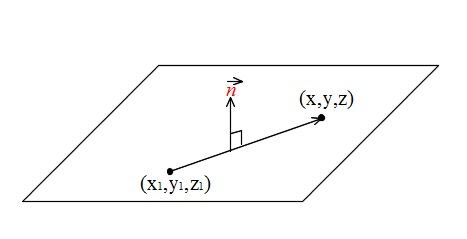
　\(\color{red}{\vec{n}}\,\)を法線ベクトルといいます。