確率で点が移動する問題ってありますよね。サイコロを何回か振ってちょうど原点に止まった、という感じの問題です。
点の移動はサイコロの出目で決まるので考え方を工夫すれば解き方は難しくはありません。
ポイントはサイコロを振る回数が整数であるということです。
サイコロを振るという試行は独立
サイコロを振る試行は「復元抽出」と同じだということは以前に説明しました。
一回一回の試行は他の試行に影響しないということです。
つまり、サイコロの出目によって点が移動する問題は、
1つひとつの確率の積で求めることができるということです。
点の移動問題のポイントは、
「回数」と「位置」です。
問題に回数が指定されている場合は、回数と最終的な位置に着目する。
回数に指定が無い場合は最終的な位置について、
\(x\)座標、\(y\)座標のように2つの条件が与えられます。
ここでは回数が指定してある問題で練習することにします。
点の移動する回数が少ない問題
\(x\) 軸上に点Pがある。
さいころを投げて6の約数の目が出たときPは \(x\) 軸の正の方向に1だけ進み、
6の約数で無い目が出たときPは \(x\) 軸の負の方向に1だけ進むことにする。
さいころを4回投げたとき、原点から出発した点Pが、原点にある確率を求めよ。
また、\(x=3 , x=-2x\) の点にある確率をそれぞれ求めよ。
このような問題は「確率の応用」となることがありますが、やるべき作業をしっかりやれば考え方は確率の基本です。
つまり、「場合」を書き出せばすぐに分かるということです。
それほど難しい問題ではありませんが、
「 \(x\) 軸」、つまり「数直線上」の問題なので数直線は書いて考えるんですよ。
6の約数が目として出たときは「正の方向に1だけ進む」
「1,2,3,6」が出たときは +1(右に1)
6の約数でない目が出たときは「負の方向に1だけ進む」
「4,5」が出たときは -1(左に1)
ということです。元は原点にあります。
4回しか投げないので数直線も+4が右端、-4が左端となる部分だけで良いです。

ここで移動4回のうち何回右と左に進むかを考えると、
右に4回のとき左に0回、このとき x =4+0=+4

右に3回のとき左に1回、このとき x =3+(-1)=+2
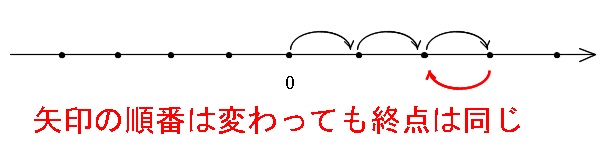
右に2回のとき左に2回、このとき x =2+(-2)=0
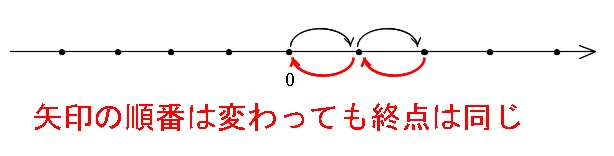
右に1回のとき左に3回、このとき x =1+(-3)=-2
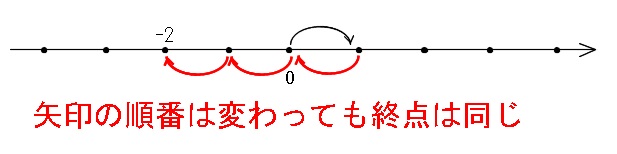
右に0回のとき左に4回、このとき x =0+(-4)=-4

の5通りしかないことが分かります。
4回投げて原点に戻るということは、「2回右、2回左」に移動する場合しかありません。
右に進む確率は \(\displaystyle \frac{4}{6}=\frac{2}{3}\)
左に進む確率は \(\displaystyle \frac{2}{6}=\frac{1}{3}\) です。
右に2回進むのが4回中どの2回なのかは
\(\displaystyle _4\mathrm{C}_2=\frac{4\cdot 3}{2\cdot 1}=6\)
よって原点に戻る確率は、
\(\displaystyle p_0=_4\mathrm{C}_2\times \left(\frac{2}{3}\right)^2\times \left(\frac{1}{3}\right)^2=\frac{8}{27}\)
次に x=3になるときですが、
+1と-1を4回組み合わせて3になる「場合」はありません。
よって、x=3となる確率は
\( \color{red}{p_3=0}\)
ある事象が起こらない場合の確率は「0」です。
x=-2となる場合は、
「4回のうち、+1が1回、-1が3回の場合だけ」
なので、+1を何回目に選ぶかを考慮して、
\(\displaystyle p_{-2}=_4\mathrm{C}_1\times \left(\frac{2}{3}\right)^1\times \left(\frac{1}{3}\right)^3=\frac{8}{81}\)
以上、「場合」を考えるだけですみます。
移動の数、サイコロを振る回数が多くなると「場合」、「すべての事象」を書き出すのに時間がかかりすぎる場合があります。
もちろん時間があれば書き出す方が確実ですが、整数の性質を利用することが多いです。
回数は「整数」回しかありませんからね。
この問題では全部で4回です。
「6の約数の目が出るとき」=「右に進む」回数を m 回とすると
「6の約数でない目が出るとき」=「左に進む」回数は 4-m 回となります。
このことを利用すると回数が多くなっても簡単に処理することが可能となりますよ。
点が移動する回数が多い問題
数直線上の原点 O に点 P がある。
点 P はさいころを投げて2以下の目が出たときは+2だけ移動し、
3以上の目が出たときは-1だけ移動する。
さいころを9回投げて移動を終了したとき点 P が原点 O に戻っている確率を求めよ。
9回という微妙な回数ですが、
時間に余裕があるときは、
迷わずすべての「場合」、「事象」を書き出しにいきましょう。
ここではもっと回数が多い場合も対応できる求め方を示します。
先ず、さいころの出目による移動ですが2通りあります。
「2以下のとき+2」と「3以上のとき-1」
それぞれの確率を出しておきましょう。
出目が2以下の確率は \(\displaystyle \frac{2}{6}=\frac{1}{3}\)
出目が3以上の確率は \(\displaystyle \frac{4}{6}=\frac{2}{3}\)
さいころを9回振るうち、
2以下の出目が出る回数を m 回とすると、
3以上の出目が出る回数は 9-m 回となります。
この関係を出しておくことがポイントです。
2以下の出目による移動は「+2が m 回」なので
\( 2\times m=2m\)
3以上の出目による移動は「-1が 9-m 回」なので
\( (-1)\times (9-m)=m-9\)
9回さいころを投げた後にはこの和だけ移動することになります。
原点に戻るということはその「和が0」になることなので
\( 2m+(m-9)=0\\ \\
\Leftrightarrow m=3\)
つまり、
「2以下の出目が3回、3以上の出目が6回」
という事象が起こったときちょうど原点に戻るということです。
その確率は、「9回中3回の出目が2以下」ということから
\(\displaystyle p_0=_9\mathrm{C}_3\left(\frac{1}{3}\right)^3\left(\frac{2}{3}\right)^6=\frac{1792}{6561}\)
と求めることができます。
求め方は事象すべてを書き出してもかまいません。
練習段階においてはむしろその方が「書き出す」という作業が身について良いかもしれません。
センター試験に限らず「共通テスト」になると一層必要なことで、どちらがというより、どちらにしても大切なことですよ。
ここにある項目を外して、問題は作れません。
